2RPU/UPR+RP五自由度混联机器人静刚度分析

张东胜　许允斗　姚建涛　赵永生

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

0　引言

与串联机器人相比，并联机构具有结构紧凑、承载能力大、刚度大的特点[1-2]，在零部件的精密加工、医疗、重载设备的运动仿真等领域有较高的应用价值，比较典型的并联设备如Gough发明的六自由度(degree-of-freedom, DOF)Stewart运动仿真平台[3]、Clavel设计的3-DOF Delta并联机构[4]等。另一方面，与并联机构相比，串联机器人具有控制简单、灵活度高、工作空间大的特点[5]，在码垛、喷涂、包装、搬运、装配等领域得到了广泛应用，比较典型的串联机器人如SCARA串联机械臂[6]、UR系列六自由度串联机械臂[7]。

随着社会的高速发展，尤其是工业、航空航天、军事等领域所涉及加工任务的复杂性的增大，工作任务对机器人的性能要求不断提高。而近年来混联机器人的出现填补了这一方面的空白，其中串并混联机器人综合了并联机构刚度大和串联机器人灵活性好的特点[8-10]，成为机构学领域的新方向和现代工业制造的标志。比较典型的混联机器人有基于2UPR/SPR(R为转动副、U为虎克铰、S为球铰、P为移动副)构造的Exechon机器人、基于3UPS/UP构造的Tricept机器人等。

现有的关于机器人的研究大多集中于机器人运动学、动力学、构型综合及尺寸优化等，但机器人的刚度分析对机器人的加工性能有重要影响，国内外许多学者针对机构的刚度开展了一系列研究。GOSSELIN等[11]针对空间6-DOF并联机构提出两种分别适用于刚性机构和柔性机构的刚度模型推导方法，并推导出相应的雅可比矩阵；LIAN等[12]借助虚功原理和变形叠加法，建立了5-DOF并联机构在考虑重力情况下的半解析刚度模型；胡波等[13]基于广义力和驱动力之间的映射矩阵，得到了适用于少自由度并联机构的静刚度模型；陶兆胜等[14]、路曼等[15]利用机构变异方法设计了构型为 2RPU/RPS的并联机构，并将机构划分成若干子系统，计入关节和支链弹性对整机刚度的影响，采用子结构综合技术建立该并联模块的刚度模型；LU等[16]在考虑分支的惯性力、驱动力及约束力的前提下，推导出了并联机构刚度的统一模型；张俊等[17]分别采用虚拟关节法和有限元法计入各关节和支链体的柔性，并通过推导动平台和支链装配体间的变形协调方程构建出Exechon并联模块的弹性静力学模型。此外，汪满新等[18]在完成2-DOF并联机构位置逆解分析和变形分析的基础上，基于全变形雅可比矩阵建立了4-DOF混联机器人静刚度半解析模型；王友渔等[19]借助子结构综合思想和ANSYS参数化设计语言，构造了两种可重构5-DOF混联机械手模块的有限元模型；WU等[20]运用子部件装配法，研究了含有冗余驱动的5-DOF混联机器人的刚度模型；SUN等[21]利用子结构柔顺模型建立了一种5-DOF摩擦搅拌焊机器人的半解析刚度模型。

综上可知，现有的研究主要集中于并联机构的刚度分析，且很多研究在对基于少自由度并联机构构造的五自由度混联机器人刚度进行分析时，忽略了串联环节对机器人刚度的影响，仅针对少自由度并联部分进行了刚度分析。针对混联机器人，尤其是五自由度混联机器人的刚度特性分析相对较少。

由于机器人的静刚度随其自身位姿的变化而变化，本文以基于3-DOF并联机构2RPU/UPR构造的5-DOF混联机器人为研究对象[22-23]，求得并联机构分支和串联部分单自由度摆头的柔度矩阵以及并联部分与串联部分两子系统的静刚度模型，建立了混联机器人的整体刚度模型。

1　机构描述及坐标系建立

如图1a所示，该五自由度混联机器人包括2RPU/UPR并联机构，摇摆头、移动平台和机架，其结构简图见图1b。该五自由度混联机器人中并联部分的定平台、动平台为等腰三角形；机构中的每条分支均由上连杆与下连杆组成，上连杆连接定平台一侧，下连杆连接动平台一侧。分支1、3为RPU结构，分支2为UPR结构。在RPU分支中，R副轴线与U副连接下连杆的轴线相互平行；U副连接动平台的轴线共线；P副轴线分别与相应分支中的R副轴线及U副连接下连杆轴线相互垂直。在UPR分支中，R副轴线与RPU分支中的U副连接动平台的轴线平行；U副连接定平台的轴线与RPU分支中R副轴线平行；P副轴线与该分支中R副轴线及U副连接上连杆轴线相互垂直。

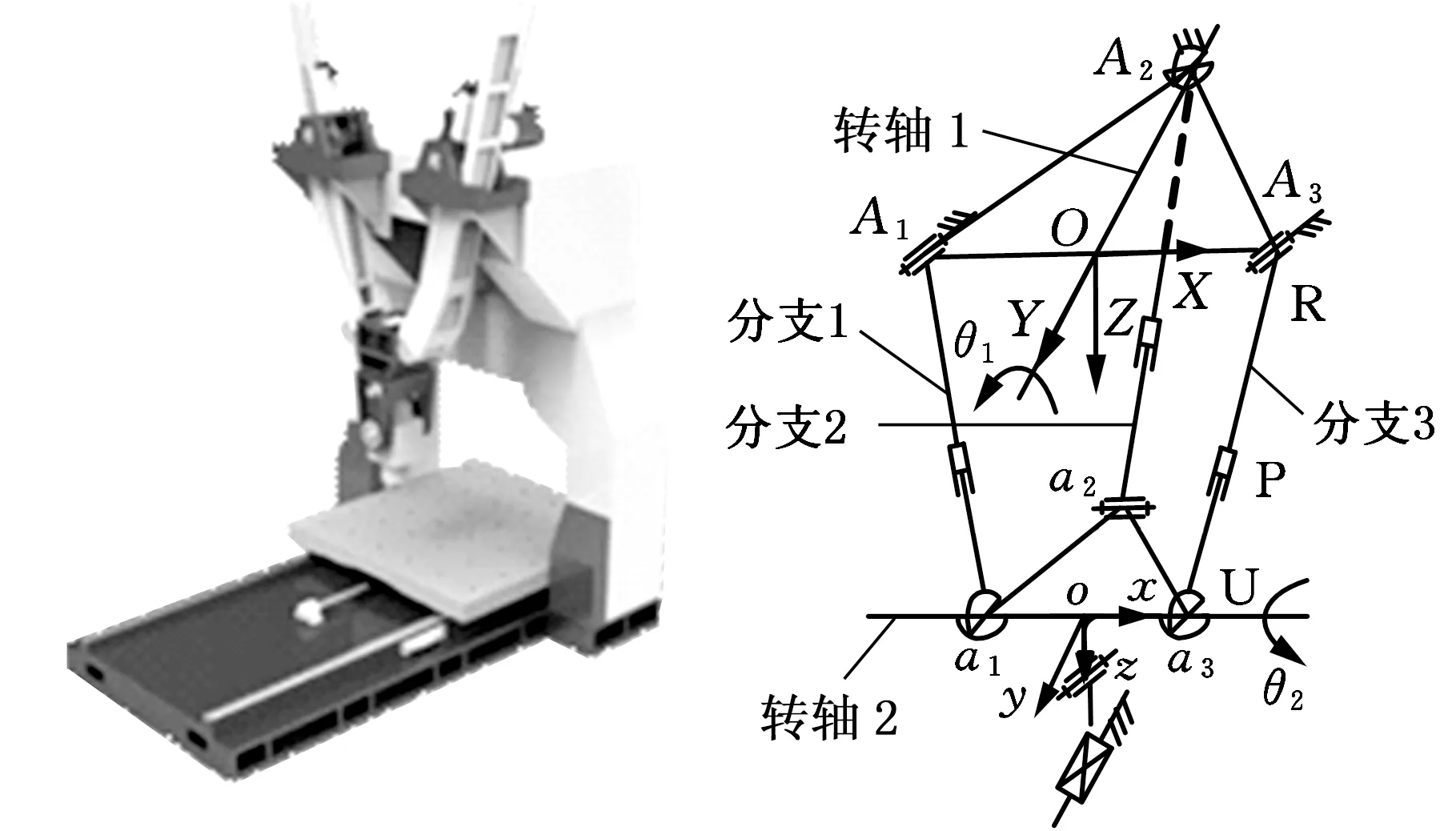
(a)三维模型　　　　　　　(b)结构简图图1　5-DOF混联机器人构型Fig.1　Configuration of the 5-DOF hybrid manipulator

由图1结构可知：2RPU/UPR机构具有两转一移三个自由度，分别为绕定平台Y轴的转动、绕动平台x轴的转动以及沿定平台Z轴的移动。绕x轴转动可实现动平台绕x轴方向的姿态调整，而绕Y轴的转动可实现沿X轴方向的大范围移动，故在动平台上串接一个轴线与靠近定平台转轴平行的单自由度摆头，用于末端刀具另一个方向的姿态调整，沿Y轴安装一个可移动工作台，从而实现混联机器人的五轴联动。为便于分析，定义A1、A2、A3分别为3条分支杆与定平台相连的运动副的中心点；a1、a2、a3分别为其与动平台相连的运动副的中心点；在定平台上定义定系{N}：OXYZ，X轴与A1A3重合，Z轴垂直于定平台，Y轴符合右手定则；在动平台上定义动系{n}：oxyz，x轴与a1a3重合，z轴垂直于动平台，y轴符合右手定则。

2　运动学分析

混联机器人的刚度分析涉及机器人的位置反解，所以为了便于该混联机器人的刚度分析，在此对该混联机器人的位置反解进行简单分析。该5-DOF混联机器人的移动工作台与其余部分相比，具有运动独立性，所以接下来的分析忽略移动工作台的运动。如图2所示，设机器人末端参考坐标系{r}：o1x1y1z1在定系{N}中的位置向量为P1=(x1，y1，z1)T，姿态矩阵为R1=[lmn]，其中l、m、n分为代表机器人末端姿态向量。

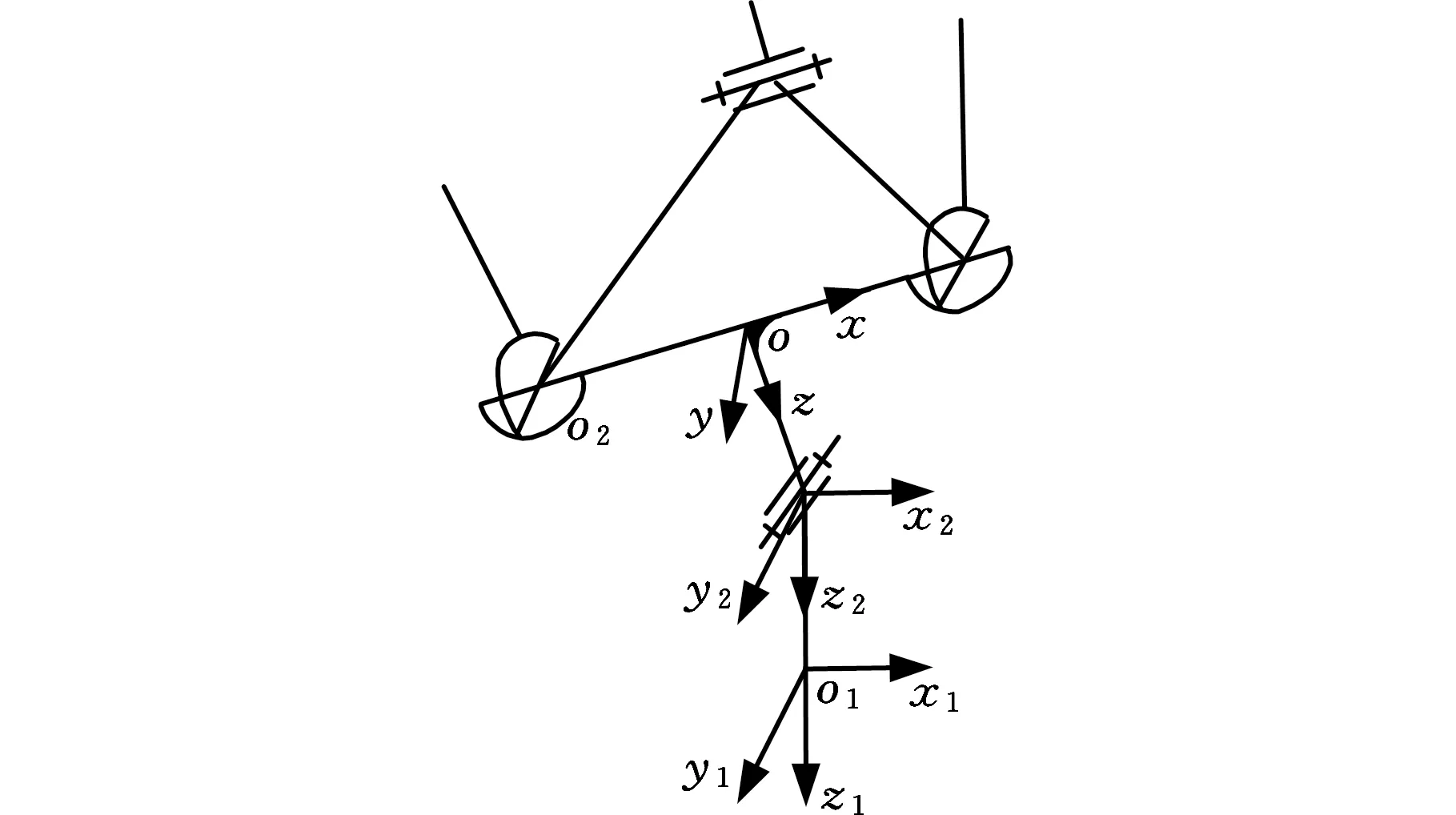
图2　摆头姿态描述Fig.2　Orientation description of the swing head

设单自由度摆头和动平台连接转动副中心点o2在参考坐标系{r}中的位置向量为P0,在定系{N}中的位置向量为P2，可表示为

P2=R1P0+P1

(1)

P0=(0，0，-l4)T

设由式(1)求得的位置向量P2=(x2，y2，z2)T，根据并联机构2RPU/UPR的结构约束可知

(2)

式中，l4为o2点到o点的距离；θ1为动平台绕Y轴的转角；θ2为动平台绕x轴的转角。

因为动平台姿态可通过绕两条连续转轴的转角θ1和θ2得到，所以动平台相对定平台的旋转变换矩阵为

(3)

所以，oo2和o2o1之间的转角可表示为

θ3=arccos(mT·R(:,3))

(4)

式中，R(:,3)表示旋转变换矩阵R的第三列；θ3为单自由度摆头的摆角，其方向可通过向量m和R(:,3)的叉乘来判断。

类似于式(1)，可求得动平台参考点o在定系{N}中的位置矢量为

P=RP3+P2

(5)

P3=(0，0，-l2)T

式中，l2为o点到o2点的距离。

根据机构几何特点，Ai点位置矢量在{N}系中可表示为

NAi=(ai，bi，0)T

(6)

i=1,2,3a2=b1=b3=0

ai点位置矢量在{n}系中可表示为

nai=(pi，qi，0)T

(7)

p2=q1=q3=0

ai点位置矢量在{N}中可表示为

Nai=Rnai+P

(8)

进而，当已知动平台的位置P和姿态R时可求得三条支链的长度：

li=|Nai-NAi|

(9)

3　静刚度分析

不同于并联机构/串联机构的刚度分析，混联机器人揉合了并联和串联机构的特点，增加了混联机器人的刚度建模难度。为初步了解该混联机器人的刚度特性，将分别求解并联部分与串联部分的静刚度模型，从构造系统的力旋量系和弹性变形协调条件入手，快速且简单地建立混联机器人的刚度模型，并据此揭示整机静刚度在任务空间中随位形变化的规律。

3.1　2RPU/UPR静刚度分析

为实现快速评估2RPU/UPR并联机构的刚度特性，简化刚度建模过程，合理的结构假设可较大程度上降低分析难度[24]。几项基本假设如下：

(1)机构中各分支杆均视为规则截面的均质杆，且忽略机构中的铰链摩擦和轴承接触变形；

(2)混联机构的分支均视为末端受到六维外力的杆件，其变形均视为在弹性小变形范畴内，变形线性叠加原理成立；

(3)将定平台和动平台视为刚体，忽略其因弹性变形对机构末端变形产生的影响。

当符合上述假设的杆件末端受到广义的六维外力作用时，如图3所示，可将分支杆等效为悬臂梁的受力问题，在分支杆末端会产生包含拉伸、扭转、弯曲等相应的六维变形。对于较规则的杆件而言，基于上述假设及理论力学的基本知识，可建立分支杆的六维柔度矩阵，从而得到分支杆的刚度矩阵。

图3　简化分支受力模型Fig.3　Force model of the simplified limb

(10)

式中，Ix、Iy为支链的截面惯性矩；Ip为支链的截面极惯性矩；li、S分别为第i分支的长度与横截面积；E、G分别为支链材料的弹性模量与切变模量。

图4　动平台受力模型Fig.4　Force model of the moving platform

支链末端作用在六维外力后，支链末端在符合上述假设条件下产生的总变形Xi与其所受力Fi的关系式为

Xi=CiFi

(11)

动平台和分支末端的关联点与动平台本身有相同的角位移，且关联点的线位移与动平台线位移和角位移均有关系。设X为动平台的总位移，则动平台位移和分支末端关联点位移之间满足

X=JiXi

(12)

式中，Ji为分支杆末端参考坐标系与动平台动系之间的位移变换矩阵。

Ji表达式如下：

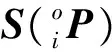
(14)

由图4可知，作用于动平台参考点o的六维外力为F，由上述可知，由外力引起的三条分支末端的约束反力为-Fi，则根据动平台受力平衡可得

(15)

式中，JFi为分支杆末端参考坐标系与动平台动系之间的力/力矩变换矩阵。

JFi表达式如下：

(16)

联立式(11)和式(12)可知

(17)

将式(17)代入式(15)可得

(18)

所以并联机构的整体刚度矩阵可表示为

(19)

当给定并联机构动平台所受外力时，可根据式(18)求得动平台的六维变形。

3.2　单自由度摆头静刚度分析

如图5所示，单自由度摆头和动平台通过转动副相连。为方便单自由度摆头刚度建模与分析，将单自由度摆头和动平台分离处理，可用于直观展示运动副部分的内力，进而将单自由度摆头末端的力等效到动平台所受外力。

图5　摆头受力模型Fig.5　Force model of the swing head

参考上述并联部分刚度分析过程可知，单自由度摆头末端受到六维外力作用后，摆头末端的变形和受力满足

Xo=CoFo

(20)

式中，Xo为单自由度摆头的六维变形；Fo为单自由度摆头末端受到的六维外力；Co为单自由度摆头的六维柔度矩阵。

Co表达式如下：

Co=

(21)

式中，Ixo、Iyo为单自由度摆头的截面惯性矩；Ipo为单自由摆头的截面极惯性矩；l5、So为单自由度摆头的长度与横截面积；Eo、Go为单自由度摆头材料的弹性模量与切变模量。

类似于式(18)，式(20)可整理为

Fo=KoXo

(22)

式中,Ko为单自由度摆头的刚度矩阵。

Ko表达式为

(23)

3.3　混联机器人静刚度模型

上述动平台参考坐标系原点o的等效外力F是由单自由度摆头末端的外力Fo引起的，转换关系如下：

(24)

式中，JFo为动平台参考坐标o2x2y2z2(建立在连接动平台与单自由度摆头转动副处)与单自由度摆头末端参考坐标系o1x1y1z1之间的力变换矩阵；JF为动平台动系oxyz和动平台参考坐标o2x2y2z2之间的力变换矩阵。

JFo表达式如下：

(25)

对比式(13)和式(16)可知

Ji=(JFiT)-1

(26)

所以结合式(12)和式(26)，可将由等效外力F引起的变形X转换到单自由度摆头末端的微变形[26]，其表达式为

(27)

根据各部件的变形叠加原理，结合式(20)和式(27)可得混联机器人末端的总弹性变形：

mX=Xp+Xo

(28)

上述混联机器人末端变形的求解过程如图6所示。图6中，J*(*代表i，j，f，p等)为映射矩阵。

图6　刚度建模流程图Fig.6　Flow chart of stiffness modeling

4　数值仿真

为便于仿真验证，整理上述结构参数，定平台铰链中心点的坐标为A1(-0.41，0，0)m，A2(-0.41，-0.506 0)m，A3(0.41，0，0)m；动平台铰链中心点的坐标在动系中为a1(-0.2，0，0)m，a2(0，-0.246 0)m，a3(0.2，0，0)m；初始位置中动平台连体坐标系o点坐标在定系中满足o=(0，0，1.14)m；l4=0.08 m，l5=0.12 m；分支杆的弹性模量E=2.11×1011Pa，分支杆的横截面积S=1.96×10-3m2，截面惯性参数Ix=Iy=2Ip=3.07×10-7m4，切变模量G=7.57×1010Pa。设作用在摆头末端的广义外力F=(200，200，200)TN，广义外力矩T=(40，-40，0)TN·m。五自由度混联机器人的动平台和单自由度摆头的刚度相对其他部件较高，所以以机器人初始位姿为例，按上述给定参数建立混联机器人的简化模型，然后对其进行刚体处理，并借助SolidWorks Simulation静力学仿真软件对其进行仿真，结果如图7所示。

(a)X方向微位移

(b)Y方向微位移

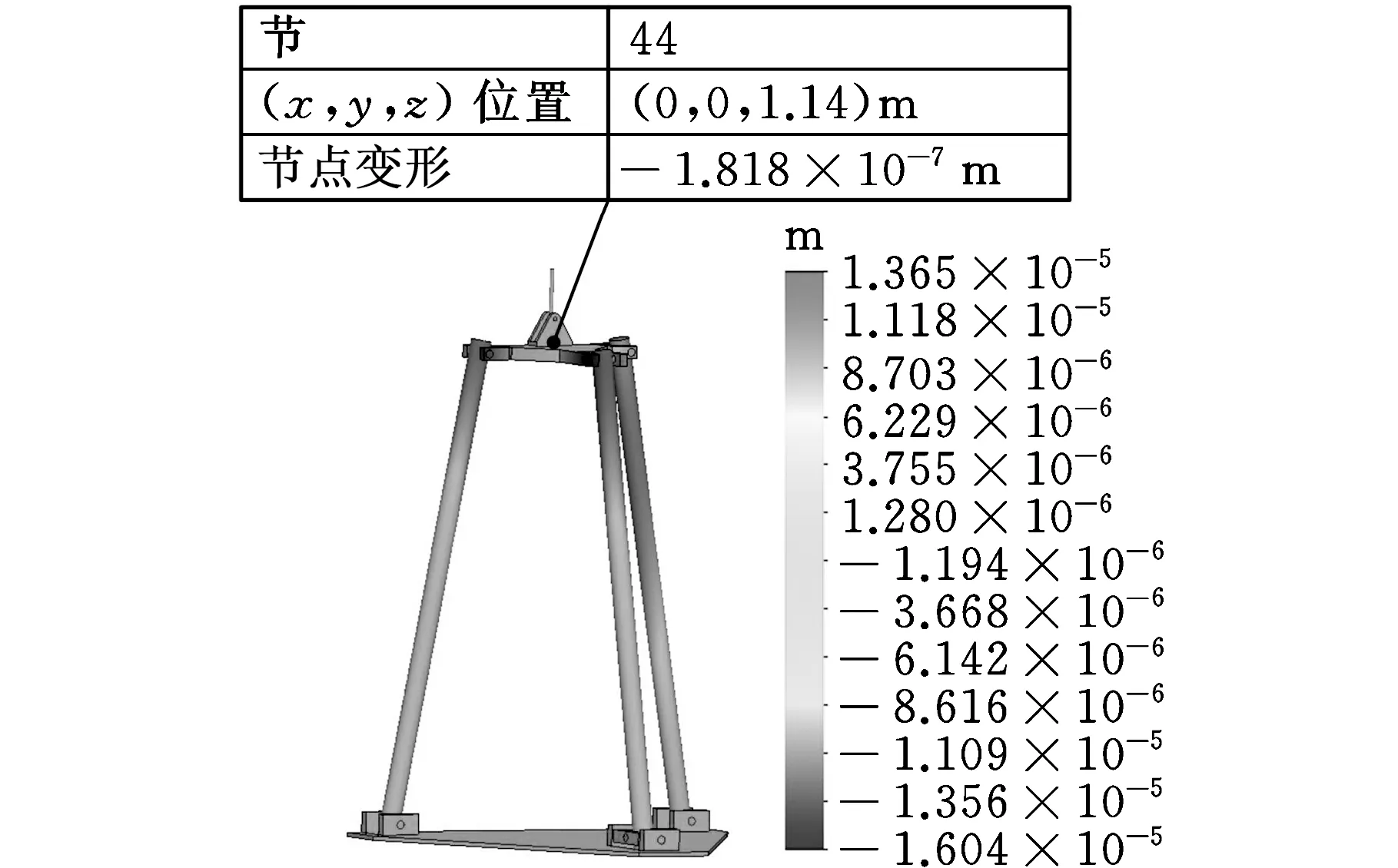
(c)Z方向微位移图7　5-DOF混联机器人微位移图Fig.7　Micrometric displacement of the 5-DOF hybrid manipulator

图7给出了动平台参考点o在基坐标系中的微位移。为了达到相互验证的目的，运用上述参数，借助MATLAB软件进行解析计算。将解析结果和图7中有限元计算结果进行对比，如表1所示。

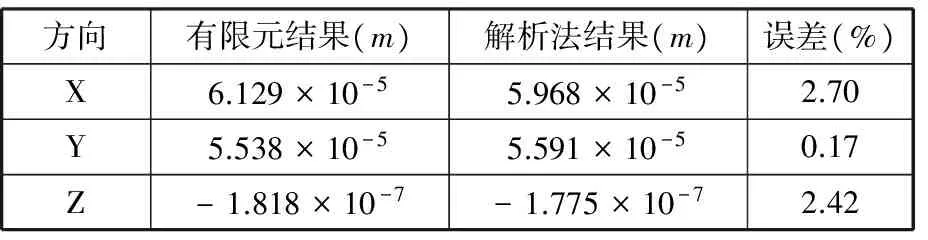
表1　有限元法及解析法结果对比Tab.1　Results comparison between finite element method and analytical method

对比分析表1中有限元和解析法结果可知，两种方法求得的结果吻合，误差小于5%，证明该方法可用于快速建立五自由度混联机器人的刚度模型，具有一定的实用性。

为了进一步体现该五自由度混联机器人的刚度特性，规划一任务工作空间：单自由度摆头垂直于并联机构动平台(鉴于单自由度摆头驱动关节刚度较大，在此忽略该自由度θ3对整体机构的影响)，动平台绕转轴1的转动范围-30°≤θ1≤30°，动平台绕转轴2的转动范围-15°≤θ2≤15°，动平台参考点o的坐标分量z=1.14 m。该五自由度混联机器人的刚度分布如图8所示。

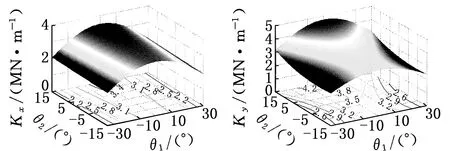
(a)X方向线刚度(b)Y方向线刚度

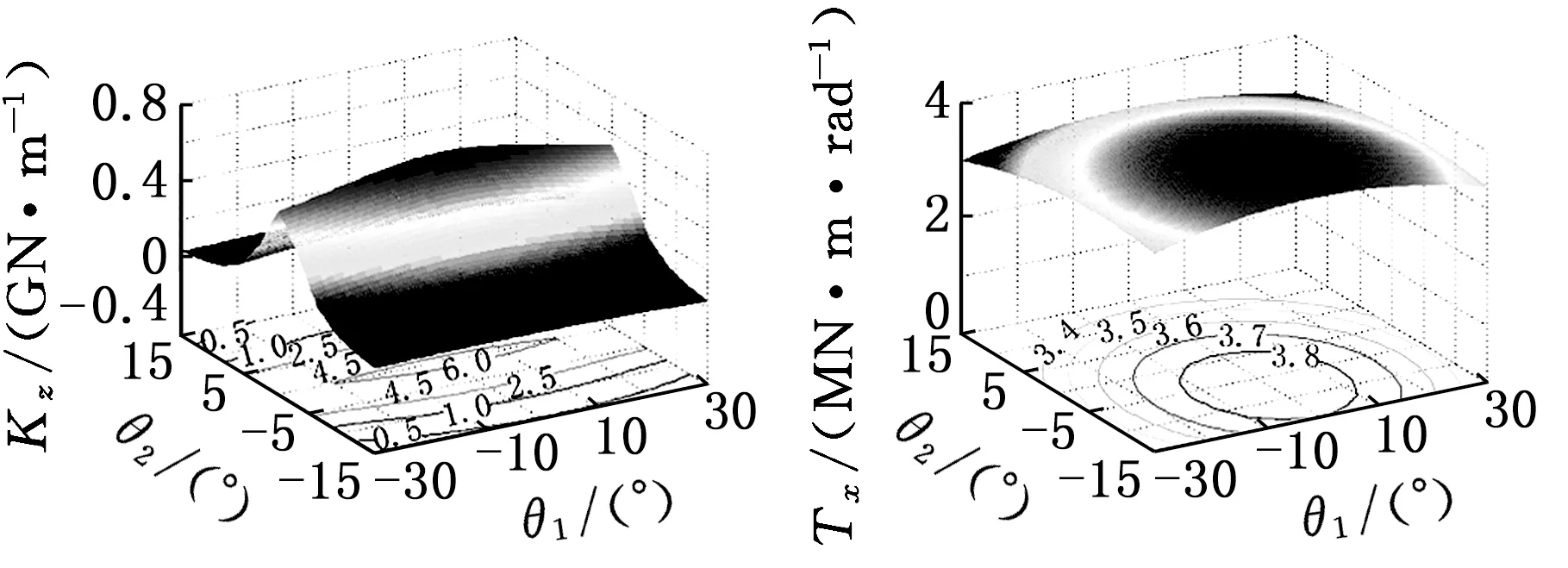
(c)Z方向线刚度(d)X方向角刚度

(e)Y方向角刚度(f)Z方向角刚度图8　5-DOF混联机器人刚度分布图Fig.8　Stiffness distribution of the 5-DOF hybrid manipulator

图8给出了该五自由度混联机器人在预定工作空间范围内的刚度分布情况，结合图中刚度分布曲面及刚度图谱可以更好地了解该混联机器人的刚度，为充分发挥机器人的刚度性能提供必要参考。

5　结论

(1)本文对5-DOF混联机器人的构型进行了描述，借助串联和并联结构独立求解思想，建立了5-DOF混联机器人的位置反解模型。

(2)简化5-DOF混联机器人刚度建模过程，给出基本假设条件，结合螺旋理论和材料力学的知识，分别求得并联机构分支和串联部分单自由度摆头的柔度矩阵，进而得到并联部分和串联部分两子系统的静刚度模型。

(3)从构造系统的力旋量系和弹性变形协调条件入手，将并联模块的微变形转换至单自由度摆头末端，并通过变形叠加原理与串联部分微变形相结合，得到该五自由度混联机器人的总体变形。

(4)利用有限元和MATLAB仿真软件对典型位姿下混联机器人在外力/力矩影响下产生的微位移进行仿真验证，并给出了整机静刚度在任务空间中随位姿变化的刚度分布图。

参考文献：

[1]MERLET J P. ParallelRobots[M]. Dordrecht：Springer Science & Business Media, 2012： 12-17.

[2]宋轶民, 翟学东, 孙涛,等. 一种三自由度冗余驱动并联模块的刚度分析[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(1):25-32.

SONG Yimin, ZHAI Xuedong, SUN Tao, et al. Stiffness Analysis of a 3-DOF Redundantly Actuated Parallel Module[J]. Journal of Tianjin University (Science and Technology), 2015, 48(1): 25-32.

[3]CAO Y, JI W, ZHOU H, et al. Position-singularity Analysis of 6-3 Stewart-Gough Parallel Manipulators for Special Orientations[J]. International Journal of Robotics and Automation, 2011, 26(2): 152-158.

[4]梅江平, 臧家炜, 乔正宇,等. 三自由度Delta并联机械手轨迹规划方法[J]. 机械工程学报, 2016, 52(19): 9-17.

MEI Jiangping, ZANG Jiawei, QIAO Zhengyu, et al. Trajectory Planning of 3-DOF Delta Parallel Manipulator[J]. Journal of Mechanical Engineering, 2016, 52(19): 9-17.

[5]TSAI L W. Robot Analysis: the Mechanics of Serial and Parallel Manipulators[M]. John Wiley & Sons, 1999： 19-27.

[6]FANG J, LI W. Four Degrees of Freedom SCARA Robot Kinematics Modelling and Simulation Analysis[J]. International Journal of Computer, Consumer and Control, 2013, 2(4): 20-27.

[7]KEBRIA P M, AI-WAIS S, ABDI H, et al. Kinematic and Dynamic Modelling of UR5 Manipulator[C]// Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics. Washington DC, 2016: 004229-004234.

[8]ZHANG D, XU Y, YAO J, et al. Kinematics,Dynamics and Stiffness Analysis of a Novel 3-DOF Kinematically/Actuation Redundant Planar Parallel Mechanism[J]. Mechanism and Machine Theory, 2017, 116: 203-219.

[9]ZHANG J, ZHAO Y, JIN Y. Kinetostatic-model-based Stiffness Analysis of Exechon PKM[J]. Robotics and Computer-Integrated Manufacturing, 2016, 37: 208-220.

[10]胡波, 宋春晓, 张庆铃, 等. 2(2-UPR+SPR)串并联机构雅可比矩阵的建立[J]. 中国机械工程, 2015,26(7): 853-858.

HU Bo, SONG Chunxiao, ZHANG Qingling, et al. Jacobian Matrix Establishment of 2(2-UPR+SPR) Serial-parallel Manipulator[J]. China Mechanical Engineering, 2015,26(7): 853-858.

[11]GOSSELIN C M, ZHANG D. Stiffness Analysis of Parallel Mechanisms Using a Lumped Model[J]. International Journal of Robotics & Automation, 2002, 17(1): 17-27.

[12]LIAN B, SUN T, SONG Y, et al.Stiffness Analysis and Experiment of a Novel 5-DOF Parallel Kinematic Machine Considering Gravitational Effects[J]. International Journal of Machine Tools and Manufacture, 2015, 95: 82-96.

[13]胡波, 路懿. 基于广义力的少自由度并联机构的静刚度统一模型[J]. 中国科技论文, 2009, 4(8): 592-598.

HU Bo, LU Yi. Unified Stiffness Model for Limited-DOF Parallel Manipulators[J]. China Sciencepaper, 2009, 4(8): 592-598.

[14]陶兆胜, 彭澎, 赵艳芹. Exe-variant并联模块静刚度分析[J]. 农业机械学报, 2017, 48(4): 377-382.

TAO Zhaosheng, PENG Peng, ZHAO Yanqin. Stiffness Analysis for Exe-variant Parallel Kinematic Machine[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(4): 377-382.

[15]路曼, 赵艳芹. 类Exechon并联模块的结构设计与刚度建模[J]. 农业机械学报, 2016, 47(3):367-372.

LU Man, ZHAO Yanqin. Structural Design and Stiffness Modeling for Exe-variant Parallel Kinematic Machine[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3):367-372.

[16]LU Y, DAI Z, YE N. Stiffness Analysis of Parallel Manipulators with Linear Limbs by Considering Inertial Wrench of Moving Links and Constrained Wrench[J]. Robotics and Computer-Integrated Manufacturing, 2017, 46: 58-67.

[17]张俊, 赵艳芹. Exechon并联模块的静刚度建模与分析[J]. 机械工程学报, 2016, 52(19): 34-41.

ZHANG Jun, ZHAO Yanqin. Stiffness Modeling and Evaluation for Exechon Parallel Kinematic Machine Module[J]. Journal of Mechanical Engineering, 2016, 52(19): 34-41.

[18]汪满新, 王攀峰, 宋轶民,等. 4自由度混联机器人静刚度分析[J]. 机械工程学报, 2011, 47(15): 9-16.

WANG Manxin, WANG Panfeng, SONG Yimin, et al. Stiffness Analysis of a 4-DOF Hybrid Robot[J]. Journal of Mechanical Engineering, 2011, 47(15): 9-16.

[19]王友渔, 赵兴玉, 黄田,等. 可重构混联机械手TriVariant与Tricept的静动态特性预估与比较[J]. 天津大学学报(自然科学与工程技术版), 2007, 40(1): 41-45.

WANG Youyu, ZHAO Xingyu, HUANG Tian, et al. Estimation and Comparison of Static and Dynamic Performance of Two Reconfigurable Hybrid Robots-the Trivariant and the Tricept[J]. Journal of Tianjin University(Science and Technology), 2007, 40(1): 41-45.

[20]WU Jun, WANG Jinsong, WANG Liping, et al. Study on the Stiffness of a 5-DOF Hybrid Machine Tool with Actuation Redundancy[J]. Mechanism and Machine Theory, 2009, 44(2): 289-305.

[21]SUN T, WU H, LIAN B, et al. Stiffness Modeling, Analysis and Evaluation of a 5 Degree of Freedom Hybrid Manipulator for Friction Stir Welding[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016: 0954406216668911.

[22]张东胜, 许允斗, 姚建涛,等. 5自由度混联机器人逆动力学分析[J]. 农业机械学报, 2017, 48(9): 300-307.

ZHANG Dongsheng, XU Yundou, YAO Jiantao, et al. Inverse Dynamic Analysis of a Novel 5-DOF Hybrid Manipulator [J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(9): 300-307.

[23]LI Q, HERVÉ J M. Type Synthesis of 3-DOF RPR-equivalent Parallel Mechanisms[J]. IEEE Transactions on Robotics, 2014, 30(6): 1333-1343.

[24]PASHKEVICH A, CHABLAT D, WENGER P. Stiffness Analysis of Overconstrained Parallel Manipulators[J]. Mechanism and Machine Theory, 2009, 44(5): 966-982.

[25]李立建, 马爱霞, 姚建涛,等. 柔性并联六维力传感器力映射解析研究[J]. 机械工程学报, 2017, 53(7): 30-38.

LI Lijian, MA Aixia, YAO Jiantao, et al. Force Mapping Analytical Research of Flexure Parallel Six-axis Force/Torque Sensor[J]. Journal of Mechanical Engineering, 2017, 53(7): 30-38.

[26]赵永生, 许允斗，姚建涛, 等. 一种过约束并联机构受力分析的方法[J]. 中国机械工程, 2014, 25(6): 711-717.

ZHAO Yongsheng, XU Yundou, YAO Jiantao, et al. A Force Analysis Method for Overconstrained Parallel Mechanisms[J]. China Mechanical Engineering, 2014, 25(6): 711-717.

(编辑王旻玥)