小学数学教学中的操作与说理——以“圆锥的体积”的教学为例

◇游 迪

关于圆锥体积的计算方法，不同版本的小学数学教材中比较一致地给出以下“证明”方法：用圆锥形的容器装满沙子或水倒入与它等底等高的圆柱形容器中，从而发现圆锥的体积是和它等底等高的圆柱的体积的三分之一。以北师大版教材为例，具体呈现形式如图1所示：

图1

然而，在实际教学过程中，往往会有一些“意外”。出于安全考虑，教师给学生提供的圆锥、圆柱形容器一般都比较厚（防止割到学生的手），学生实际操作时常常会发现在经历过3次“用圆锥形容器装满沙子倒入圆柱形容器”的操作后，还是无法完全将其填满。此时，教师就强调：“因为测量有误差，其实正确的答案就是3次填满。”

在一次“圆锥的体积”公开课中，一个“不肯屈服”的学生提出了自己的困惑：“老师，我们各小组用圆锥形杯子倒了3次都没有把圆柱形杯子倒满，圆柱的体积是不是比和它等底等高的圆锥的体积的3倍大一些呢？”面对学生这样的困惑，执教教师很为难。在这里，理论上圆柱的体积确实是和它等底等高的圆锥的体积的3倍，所以，教师会要求学生考虑实际测量产生的误差。但是在前面圆周率教学的操作中，教师要求学生保留测量中小数点后面的部分。同样是操作，在不同的情形下，却有不一样的处理，这让学生无所适从。

在本文中，我们将围绕数学教学中的操作与说理，从数学分析、认知分析及教学分析这三个角度来谈“圆锥的体积”这一内容的教学。

一、数学分析

人类在很久以前就已经开始探索圆锥的体积了，最初人们对于圆锥的体积的认识就是从它与圆柱的体积的关系当中得到的。譬如，大约2000年前，欧几里得的《几何原本》中第12卷命题10即：“任何圆锥是与它同底等高的圆柱的体积的三分之一。”[1]接着利用反证法证明了圆锥的体积既不能大于和它同底等高的圆柱的体积的三分之一，也不能小于和它同底等高的圆柱的体积的三分之一，从而等于和它同底等高的圆柱的体积的三分之一（由于证明过程较长，因此在本文中不具体呈现）。同样地，在中国古代数学专著《九章算术》中，也给出了这样的命题[2]。

圆锥的体积也可以利用微积分的方法求得。具体求解过程请参阅参考文献[3]。

此外，还可以从图形运动的角度理解圆锥的体积与圆柱的体积的关系。我们知道，圆柱可以看作是由长方形绕着长或宽旋转一周而形成的，圆锥可以看作是由直角三角形绕着一条直角边旋转一周而形成的。既然圆柱与圆锥可以通过“面动成体”而得到，那么，旋转而成的几何体的体积应该与“面”和“运动”两个要素有关，即与旋转面的面积及旋转面旋转一周所经过的距离有关。[4]图2中的直角三角形BCD与长方形ABCD绕直线l旋转一周可以分别得到圆锥和圆柱。为了讨论方便，我们可以先比较三角形ABD与三角形BCD绕直线l旋转一周的情况。两个三角形的面积相等，因此只需比较它们绕直线l旋转一周所经过的距离。可以选择两个三角形的重心M、N分别代表三角形，如图3所示，容易证明MG=2NH，则点M绕直线l旋转一周的圆周长是点N绕直线l旋转一周的圆周长的2倍。由此可知，三角形ABD旋转一周后形成的几何体的体积是三角形BCD旋转一周后形成的圆锥的体积的2倍，因此圆柱的体积是与它等底等高的圆锥的体积的3倍。

图2

图3

事实上，帕普斯—古尔丁定理给出了旋转体体积的计算公式：一个平面封闭图形绕图形之外的一条直线旋转一周，旋转得到的几何体的体积等于初始面的面积乘其重心所转过的圆周的长度。根据这一公式，如图3，若CD=R,BC=h，则初始面三角形BCD的面积，点N绕直线l旋转一周所得的圆周的长度为2π·，所以三角形BCD绕直线l旋转一周后形成的圆锥的体积，为和它等底等高的圆柱的体积的三分之一。

二、认知分析

在这个案例中，学生的疑惑和教师的困惑，还可以从数学认知的角度来理解和分析。通过前面的数学分析，我们知道，让小学生理解圆锥的体积与圆柱的体积的关系的推理，是比较困难的。因此，在教学中常用的方法是通过操作让学生“看到”3倍这样的关系，但如何让学生“信服”，是教师需要考虑的。

《义务教育数学课程标准(2011年版)》中指出：“图形与几何”的教学目的是帮助学生建立空间观念，注重培养学生的几何直观与推理能力。当前义务教育阶段几何教学提倡的活动以直观体验、动手测量、模拟实验的学习方式为主。但是，教师也应该了解，义务教育阶段几何教学中通过直观体验、动手测量、模拟实验的学习活动，学习者获得的主要是感性认识；获得理性认识往往需要经历数学模型建立、推理和论证的过程。

在这个案例中，我们缺乏直接访谈学生在学习该内容时的思维过程的第一手材料，所以，下文中对学生的认知分析是基于我们的经验及对教师的访谈得出的。因此，一方面，我们希望这样的认知分析能有助于一线教师直接探知学生的思维过程。另一方面，我们希望教师能就学生学习这个内容时可能的数学认知进行更广泛的讨论。

在这个案例中，学生的困惑可能来自相关的三个方面。第一个方面，来自前面学习圆周率时操作的经验，因为圆周率是3.14…，在操作后，教师要求学生保留小数点后两位，但是在圆锥与圆柱的情境中，学生在操作后发现并不正好是3倍关系，教师却要求抹去误差，并强调正好是3倍关系。同样是操作，为什么有的情境要保留误差，而有的却要抹去？第二个方面，可能来自教师的“无理可说”。在这里，教师意识到不应该直接告知结论，希望通过操作帮助学生建构结论。然而，这里的操作却没有达到建构的目的，反而增加了如何处理误差的无所适从。第三个方面，来自操作的局限性。在这里，学生的认知结构与结论（3倍关系）还有很大的距离。操作是为了增加中间步骤，建立已有认知结构与要学的新知识之间的桥梁，但在这个情境中，对操作误差的处理消减了这个桥梁的作用。总而言之，学生产生这三个方面的困惑的根本原因在于，在学生的认知结构中，缺乏相应的数学知识来对操作的具体情境做出推理与判断。

教师的困惑，一方面，源于并不清楚学生的认知困难；另一方面，缺少改善学生认知困难的具体教学操作方法。因此，在教学中，要减少学生的疑惑，有以下两个主要途径。一方面，教师可以在教学中提高模拟实验的精确程度，尽量减小误差。1.教师课前认真准备模拟实验所用的教具，提前做几次模拟实验，改进实验细节，尽力避免实验过程中产生较大误差，保证有利于获得接近演绎推理的结果。课堂上，教师用提前实验获得的改进经验指导课堂上学生的模拟实验，可以有效提高学生模拟实验结果的精确性。2.教师在指导学生进行模拟实验时，及时指出哪些操作不当会引起差错，哪些操作可以帮助提升实验结果的准确性。3.要帮助学生建立起这样一种意识，即误差总是客观存在的，并不一定完全服从于教师所教授的数学规律，发现问题、提出质疑并找到引起误差的原因同等重要。比如，在上述例子中，学生质疑“圆锥的体积是和它等底等高的圆柱的体积的三分之一”与实验结果不符，这时，教师可以进一步引导学生提问：“如果某些学生无法得到‘圆锥的体积是和它等底等高的圆柱的体积的三分之一’这一精确结果，那么这些学生所得到的结果就完全一致吗？”这样的引导可以让学生从“对结果本身的质疑”转移到“对实验过程的反思和探究”上。在教学过程的最后，教师还可以告诉学生，数学家是用祖暅原理推理获得数量关系的精确结果的。上述所有具体的教学行为，将在一定程度上促进学生对模拟实验和演绎推理的理解、认可。另一方面，更加重要的是，教师要让学生认识到通过实验获得的数量关系主要是感性认识，因此，在教学中要给学生铺垫如何通过推理获得准确的数量关系。

三、教学分析

面对教学困境，教师需要通过数学分析和认知分析，了解相关知识的背景，认识并厘清学生学习中面临的认知困难。同时，数学分析和认知分析也提供了一些走出教学困境的方法:减小实验数据误差；做好“接受误差”的铺垫；猜想体积关系，否定不当猜想；选择适当推理、证明，师生共同推理。

总的来说，我们必须从操作与推理两方面改进教学。数学教学的实质是思维过程的教学，把知识和方法作为结果“灌输”给学生，这种方式不能够促进对学生数学思维的培养。具体的教学建议如下：

1.实验操作。

第一步（教师实验准备）：教师选取实验仪器，预做实验以减小实验数据误差。

（1）实验仪器。选取材质相同、形状标准、厚度均匀适中的等底等高的圆柱形和圆锥形容器。在学生操作前，应提醒学生思考：仪器的差异会给实验带来怎样的后果？为什么？

（2）预做实验。教师预做几次实验，根据实验结果，判断并估计学生能否合理接受。如果不能，则调整仪器或改进操作，直至得到预计学生能接受的实验结果。此时，教师要注意总结实验过程中哪些细节容易产生误差。

第二步（师生实验操作）：做好“接受误差”铺垫。事实上，学生对待实验操作结果的态度，并非总是集中在“为什么不是2倍”或“为什么不是π倍”，因为在前期的教学内容中（如长方体、正方体、圆柱的表面积、体积等）已经有针对这类困惑的教学。学生在心理上还是能够接受3倍这个结果的，但更多的会有一些“失望”的情绪，例如：为什么我从来没得到过这个结果？凭什么最终都是老师说是多少就是多少？等等。从而导致对实验操作本身兴致减弱，只是迎合教师，出现一些“伪”操作。

因此，在学生进行实验操作的过程中，适时对影响实验结果的细节进行提示，可以为合理解释带误差的实验结果做好思维铺垫。比如，在实验操作中，学生倒水或者倒沙子，可能出现圆柱的体积是圆锥的体积的2倍多但不到3倍，或者刚好为3倍，或者是3倍多一点的情况。这时，教师要及时指出学生的实验结果出现了若干种情况，并提问：“请同学们思考，引发这些不同结果的原因可能是什么？”（这样做的目的是：引导学生回想实验操作前、操作过程中教师反复指出的可能产生误差的那些细节，从而降低学生对实验结果不接受的情绪，增强学生对实验结果的认同）接下来，教师要向学生展示自己的实验结果：肉眼观察刚好是3倍。（这样做的目的是：用教师的示范，引导学生进一步合理接受实验结果，因为教师在实验仪器的选取、实验操作过程中更多地注意了减小实验误差，所以结果更接近真实值。这也为引导学生依据大家实验的结果提出猜想做好了铺垫）

2.猜想验证。

第三步（学生提出猜想）：教师提问：“根据我们实验操作的结果，让我们一起猜猜：等底等高的圆柱的体积与圆锥的体积有怎样的关系？”

这时，学生更多地会出现两种猜想：①V圆锥=，理由是，结合对图2的分析，长方形ABCD的面积是三角形BCD的面积的2倍；②V圆锥=，理由是，自己和同学们的实验操作+教师对产生误差的细节的提示+教师实验操作的结果示范。值得注意的是，由于在平时的课堂教学中，教师会反复强调“π特指圆的周长与直径的比值”这一关系，因此在实际的猜想中，很少会有学生认为等底等高的圆柱和圆锥的体积是π倍的关系。

第四步（否定不当猜想）：通过展示图形、推理、举反例，否定不当猜想。

针对部分学生的猜想①，展示如图4所示的由两个全等的正方形ADFE和BCFE拼成的长方形，使其绕直线l旋转一周，可以看出两个面积相等的正方形旋转一周后所得的几何体的体积显然不相等，正方形ADFE旋转一周后所得的几何体的体积明显更大，如图5所示。

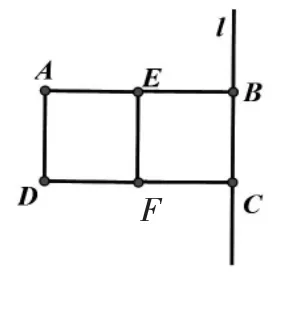
图4

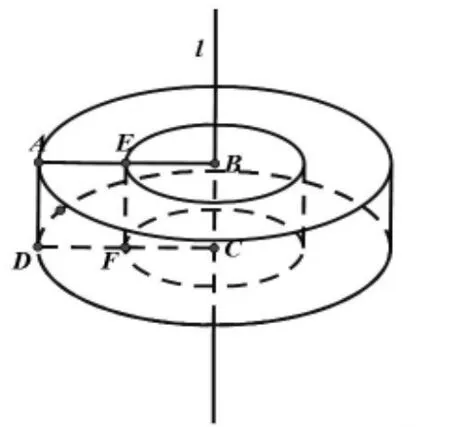
图5

在这样的基础上，可以直观展示图2中的三角形ABD和三角形BCD绕直线l旋转一周的结果（如图6），学生可以看出图6左边的几何体（阴影部分）的体积（一个圆柱挖去一个圆锥后剩下的部分）要明显大于图6右边的圆锥的体积，即圆柱的体积大于圆锥体积的2倍。这样我们就排除了猜想①。

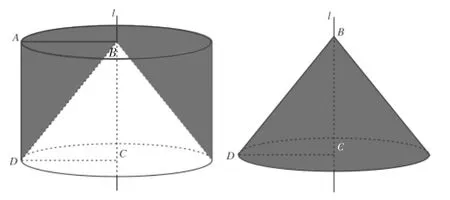
图6

从实验操作的过程和结果看，似乎猜想②是一个比较有说服力的结果。

在当前许多版本的教材（如人教版、北师大版、苏教版）中，都比较少采用上述这种动态图的形式学习体积。动态图的学习需要学生有较强的空间想象能力和对几何图形的直观感受能力，虽然小学生能够部分感悟点动成线、线动成面、面动成体这样的形式，但这种感悟不足以完全支撑起学生对面积、体积的认识与计算，需要结合教材，给予学生一些更加“直观”的展示。在教材中，通常会先约定一个或一些计量单位，再想办法用计量单位测量或计算被计量物体。可是，圆是曲线围成的，怎么拿面积单位（如1平方厘米的小正方形）摆出面积呢？于是有了“化曲为直”的方法（如图7）：

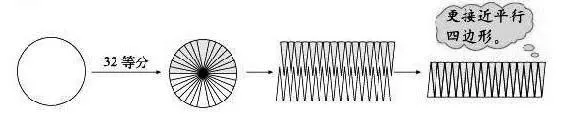
图7

抓住这个“不变的线”，再到圆柱的体积的计算，学生就会很自然地想到：化曲为直，用体积单位（如1立方厘米的小正方体）进行测量和计算（如图8）：

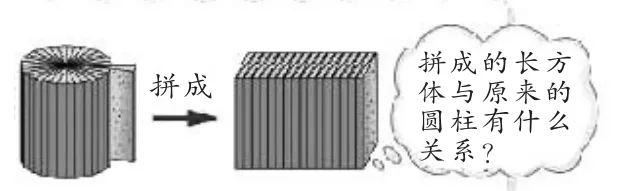
图8

在这个过程中，学生会逐步形成一定的类比推理的能力，遇到新的问题会将与其有关联的知识进行类比，从而发现新的解决方法。所以，当圆锥出现时，学生会把圆锥与同样有圆形底面和曲面侧面的圆柱进行比较，认为这两者（等底等高的圆柱和圆锥）的体积有某种关系，这是一种合理的猜想。

但目前只是猜想，究竟圆柱与圆锥的体积是怎样的关系呢？师生可以一起做一次严格的推理。

3.严密推理。

第五步（师生共同推理）：师生共同进行适当的推理和证明。选择一种在学生认知能力范围之内的圆锥的体积的推理、证明方法。以教师讲解为主，学生参与，师生共同经历严格推理、证明的过程。

基于前面的数学和认知分析，从等面积矩形在旋转半径变化时旋转体体积的关系，过渡到等面积三角形在旋转半径变化时旋转体体积的关系，并结合帕普斯—古尔丁定理与学生共同完成推理。

如图9，有三个面积相等的矩形（1）、（2）、（3），其长、宽分别满足假设正方形（1）、长方形（2）和长方形（3）绕直线l旋转一周后所得的圆柱的体积分别为V1、V2、V3。易得从而，让学生认识到：当旋转面面积相等时，旋转体的体积之比等于旋转的半径之比。

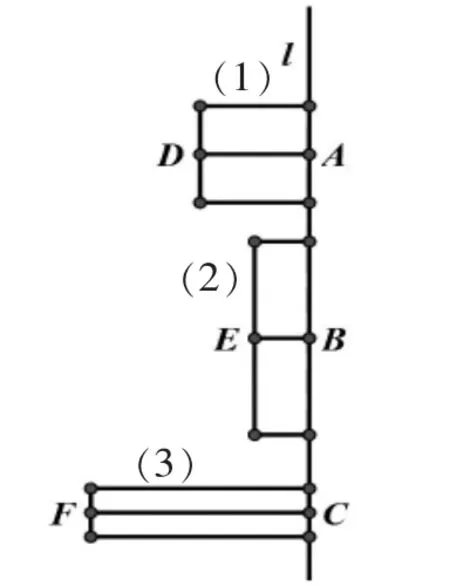
图9

再回到圆柱与圆锥的问题上来。如图2，三角形ABD与三角形BCD的面积相等。这里教师可结合图3，并结合帕普斯—古尔丁定理，与学生共同推理，得到结果：等底等高的圆柱与圆锥的体积的关系是

四、结语

经过上述数学分析、认知分析与教学分析，我们发现在数学学习中，动手操作是一种非常重要的手段，但动手操作获得的往往是感性认识、直观的结果，而严密推理论证是让学习者从感性认识、直观结果上升到理性认识，体现数学问题本质联系的重要途径。在出现不精确的结果时，必须考虑学生的认知困惑点，而不能通过直接告知让学生被动接受“精确”的结果。

数学学习中的动手操作，还需注意克服操作的形式化甚至“伪”操作的现象。例如，在三角形内角和的教学中，在要求学生把三个内角分别测量出来再相加时，学生是否真的会一个角一个角认真去量然后相加？更重要的是，学生是否真的认为三角形的内角和不是180度，而是通过操作得到的那个跟180度差一点的度数？面对这样的情形，教师可能需要在动手操作活动之前做出更好的设计，如在让学生量角的时候，可以给出三个已经从三角形上剪下来的角，而不是直接扔给学生一个三角形。

此外，从数学史的视角看，“圆锥体积的计算”是一个比较困难的问题，一般都需要在棱锥体积的基础上探讨，比如，《几何原本》与《九章算术》中都是如此。而棱锥体积的求法，一般学生要到高中阶段才会学习。如果仅仅通过操作让学生记住“圆锥的体积是和它等底等高的圆柱的体积的三分之一”这一结论，学生确实极有可能由于操作的误差带来理解上的困难。如果需要在理论上给出比较准确的结论，则必然会涉及小学生无法理解的知识。如此一来，教师教学中正确处理操作与说理变得尤为重要。

最后，想要请读者一起思考的是，从中国教材近几十年的历史看，此内容都包含在小学数学教材中，那么，在小学阶段通过这样的方式学习圆锥的体积这一内容到底有多大的必要性？具体地，小学生学习这一内容的目标是什么呢？我们以这些问题结束此文，希望读者一起思考。同样，我们也希望数学分析、认知分析及教学分析这样三个方面的思考能对广大教师成为探究型教师有益。