设计挑战性学习任务提升学生学习能力

◇沈 强

清华大学早在2008年就提出了“挑战性学习课程”（Challenge Based Learning）,力图通过有趣的、有价值的挑战性问题，来吸引学生，激发学生的好奇心和求知欲，使学生能运用综合知识获取新知识，促使学生挑战自我、主动学习，培养学生的合作能力和创新能力。作为小学数学教师，近几年我一直在努力尝试设计挑战性学习任务，让“以生为本”“积极参与”“深度思考”能在完成任务的过程中充分体现出来。

一、挑战性学习任务的内涵及价值

所谓挑战性学习任务，就是教师设计的一份学习材料，可以让学生据此进行探究性学习，以达成预期的教学目标。教师在设计挑战性任务时，不能为挑战而挑战，要从有利于课时核心目标落实出发，不是越难越好，而要遵循“入手容易、完成不易”的设计原则。任务既要让大多数学生能有成功的体验，又要留有进一步探究的空间。

二、挑战性学习任务的设计策略

1.重意义——从“技能训练”到“意义理解”的转变。

在设计挑战性任务时，既要关注学生技能的训练，更要重视学生对数学概念的理解。要利用各种材料通过变化，呈现出新的练习形式，让学生在新的情境下完成任务，这种变化不是本质上的变化，而是呈现形式上的变化，但这种变化会对学生理解数学概念的意义起着重大的作用。

如在“分数的初步认识”一课教学设计时，学生在初步认识分数的含义后，教材提供了以下习题，让学生根据分数给图形涂上颜色。（如图1）

图1

这样的习题对于巩固新知、检测学生掌握情况有着重要的作用，但是学生只要学会一一对应，犯错的机率就很小。这样的习题，做多了就如同技能训练，对分数的意义没有深层次的思考。我对习题的呈现形式进行修改，设计如下。（如图2）

对下面的这些分数，选择合适的图表示出来。

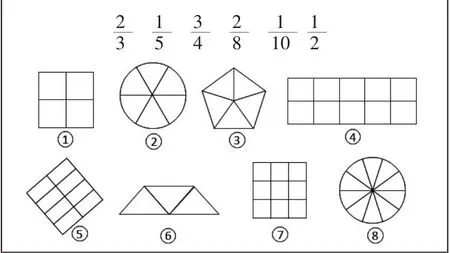
图2

与之前的习题相比，更有挑战性和层次性。在交流时，可以分为四个层次进行反馈。第一层次：给找到合适的图形，属于基本知识练习，大多数学生能找到。第二层次：思考为什么有两幅图可以表示？进一步巩固对分数本质意义的理解。第三层次：为什么②号和⑦号图形没有涂色？第四层次：有没有图形可以表示出？这样的设计，能让全体同学都参与到活动中来，有利于学生巩固知识，促使学生从技能训练向意义理解转变。

2.转方式——从“听中学”到“做中学”的改变。

美国教育家苏娜丹戴克说，告诉我，我会忘记；做给我看，我会记住；让我参加，我就会完全理解。美国教育家杜威也说过，“做中学”是比“听中学”更好的方法。传统教学中，学生长期处于师生之间一问一答的学习模式中，学生是在“听中学”，缺少提问、实践、探究的机会，慢慢也缺乏了提问的意识和探究习惯。设计挑战性任务可以改变这种学习方式，让学生通过问题引领、自主探究发现真知，真正让学生参与到学习中来，实现“做中学”。

如在教学“年、月、日”一课时，教师常用的方法是让学生对有关年、月、日的认识，通过师生问答一一呈现出来，教师将学生的回答进行分类板书。年、月、日的相关知识点多而零碎，需要学生认识大月、小月，认识平年、闰年，知道年、月、日三者之间的关系……课堂上如果采用一问一答的形式，无非是把学生已知的搬运到黑板上，不能激起他们的思考，学生的思维必定停留在浅层次上。

如何把这么多的知识点整合在一起？如何让学生对年、月、日产生一种探究的欲望？在思考与实践的过程中，我把年、月、日的认识和解决问题结合起来，设计的挑战性任务是：“爷爷有高血压，每天吃1片降压药，1盒药（30片）吃一个月够不够？”出示任务单，如图3：

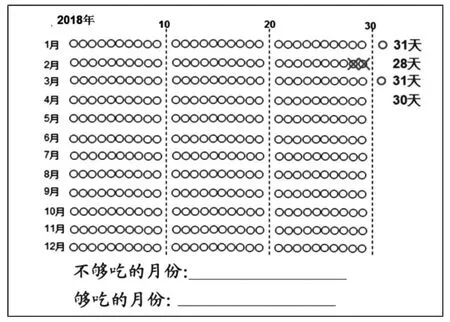
图3

让学生理解记录方式：1月份有31天，缺1片，画一个“○”表示，2月份有28天，多了两片，画两个“×”……让学生根据自己的年历本把一年的情况表示出来，观察哪些月够吃，哪些月不够吃。通过问题引领，激发求知欲，并通过数形结合的方式，让学生在探究的过程中把所涉及的知识点进行有机整合，让学生在讨论时更有聚焦点，真正实现“做中学”。

3.探未知——从“常规问题”到“非常规问题”的迈进。

数学教学既要考虑学生的已知，更要关注学生的未知。设计挑战性任务时，应打破常规的、学生熟知的情境和数学问题，增加非常规的、学生未知领域的数学问题。所谓非常规数学问题，是指无法用当前的常规方法解决，需要运用创造性思维和一系列认知策略来解决的问题。

如在教学四年级“三角形单元整理”复习课时，涉及的知识内容有很多，包含了三角形的概念、分类、内角和、三边关系等。在复习三角形分类时，教材呈现较多的是如下习题（如图4），这样的习题比较常见，学生做起来也得心应手。

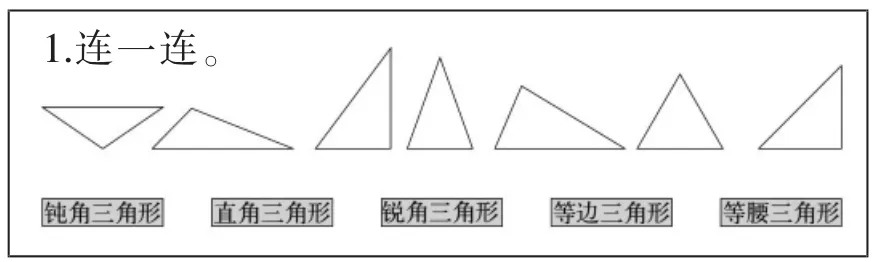
图4

在教学设计中，我设计了两个挑战性任务。任务一：从长度为18、10、8、6、6、6、2（单位：厘米）的7根小棒中选3根，可以围成几个不同的三角形？这5个三角形分别是（6、6、2）（6、6、6）（6、6、8）（6、6、10）（6、8、10）。任务二：这5个三角形按边和按角分类，分别是什么三角形？根据边的长短按角分类，是一个非常规的思考角度，打破学生的思维习惯（根据边的长短按边分类，根据角的大小按角分类），所以对学生而言是一个极具挑战性的新问题。三角形具有唯一性，三条边长度一定，这个三角形的形状与大小就能确定了，因此，从理论上说，可以把三角形根据三边长度按角分类。但思考起来不容易，需要依赖空间想象与推理能力。

4.拓思路——从“单一”向“多元”开放。

对于传统的封闭题而言，传统题已知的条件比较完备、结论确定且唯一。开放题则是“条件不完备或多余，问题不一定有解，答案不唯一”，有利于思维能力的发展和提升，是训练学生思维的有效方法之一。在设计此类挑战性任务时，首先要立足于数学教材，教材中包含了很多的例题或习题，要关注例题或习题本身所具有的思维深度和广度，教师要善于挖掘题目中的开放性元素，对习题进行大胆改编，设计符合学生实际的习题，并能让学生把思考的过程展示出来。

如在教学小数除法时，练习中安排了如下的习题（如图5）。此题是考查有关小数除法的知识，与传统的题目相比，在题型上有所创新，采用数形结合的形式来考查。但从学生解答情况来看，方法只有一种。

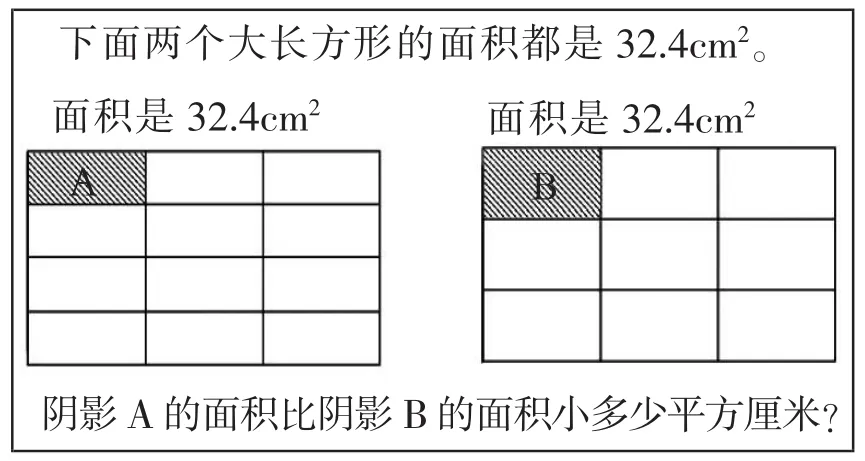
图5

学生的答案基本是这样的：32.4÷12＝2.7（cm2），32.4÷9＝3.6（cm2），3.6－2.7＝0.9（cm2）。

对该题稍作修改，将A的面积从1格扩大到2格，将B的面积从1格扩大到3格，如图6。改编后习题的解题思路，大致可以分成三大类、四个水平层次：

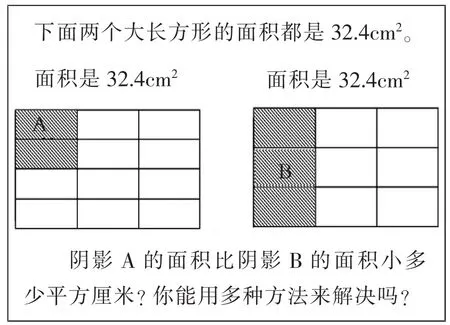
图6

第一类是分别求出阴影A和阴影B的面积，再相减。

水平层次1：阴影A，32.4÷12×2＝5.4（cm2）；阴影B，32.4÷9×3＝10.8（cm2），10.8－5.4＝5.4（cm2）。

水平层次2：阴影A，32.4÷6＝5.4（cm2）；阴影B，32.4÷3＝10.8（cm2），10.8－5.4＝5.4（cm2）。

第二类是发现阴影面积相差的部分正好等于阴影B面积的一半。

水平层次3：阴影B，32.4÷3＝10.8（cm2），10.8÷2＝5.4（cm2）。

第三类是发现阴影面积相差的部分正好等于阴影A的面积。

水平层次4：阴影A，32.4÷6＝5.4（cm2）。

除了以上几种方法，还有很多解法。改编后的习题，方法具有多样性，思维更有层次性，学生思维的宽度和深度得到锻炼，学生的思维品质得到提高。开放题解题思路的多样化，使不同的学生在思维上得到不同层次的发展。