复合材料层合板多钉连接的紧固件连接柔度

侯赤，万小朋，黄河源，倪凯强

西北工业大学 航空学院，西安 710072

钉载评估是复合材料层合板螺栓连接设计的重要环节。基于紧固件连接柔度的钉载分析技术因为效率高且不存在非线性接触所导致的收敛性问题，相对于三维有限元计算[1]或GBJM(Global Bolted Joint Model)方法[2]而言，更适合大规模复合材料结构钉群连接区的分析。紧固件连接柔度与螺栓刚度、被连接板刚度和载荷偏心度有关[3]，Tate[4]、Nelson[5]、Swift[6]和Huth[7]等从试验中总结了紧固件柔度的经验公式；Xiong[8]和舒怀等[9]利用弹性梁理论推导了连接刚度的理论公式；Siong[10]对单钉紧固件连接柔度作了有限元计算， McCarthy等[11-12]研究了钉孔间隙和摩擦对紧固件连接柔度的影响，Alkatan和Andriamampianina[13-14]研究了界面摩擦参与传载时紧固件连接柔度随疲劳载荷循环数增加而变化的规律。

紧固件连接柔度是弹簧-质量、弹簧-壳和梁-壳等模型中螺栓模拟元素刚度取值的主要依据。谢宗蕻等[15-16]采用弹簧-质量模型进行了复合材料修补结构的钉载计算和钉载优化，Olmedo等[17]将特征曲线法与弹簧-质量模型相结合，分析了复合材料销钉连接结构的刚度和强度，McCarthy等[18-19]采用弹簧-质量模型并基于损伤后结构应力-应变的二次函数关系假设，分析了多钉连接结构的极限强度。

紧固件连接柔度与连接区钉的排数相关，Morris[20]通过试验研究了金属多排钉连接结构的紧固件连接柔度与单钉连接结构的差异，并基于各排钉紧固件柔度相同的假设，拟合了紧固件连接柔度与螺栓排数的指数函数关系。但是，该函数并不适合脆性的复合材料层合板连接结构，为了建立复合材料层合板多钉连接紧固件连接柔度和单钉连接紧固件连接柔度的关系，本文以ZT7H/5429层合板1列3排螺栓连接件为对象，对各排螺栓紧固件连接柔度进行了理论求解，研究了旁路载荷和分析模型中钉间层合板柔度偏差对紧固件连接柔度取值的影响，建立了多排钉连接紧固件连接柔度的修正公式，通过紧固件连接柔度的少量迭代修正，实现了多钉连接结构钉载计算准确度的提高。

1 多钉连接中不同排紧固件连接柔度的差异性

Swift[6]和Huth[7]关于螺栓连接紧固件连接柔度的定义为

(1)

式中：Pb为紧固件所传递的载荷；δ为连接点处被连接板的相对位移。由于多钉连接结构中钉间层合板相对位移难以测量，不能直接使用式(1)计算各排钉紧固件连接柔度，因此本文基于弹簧-质量模型对紧固件连接柔度进行反演计算。

1.1 复合材料层合板1列3钉连接件拉伸试验

图1(a)所示1列3排双搭接螺栓连接试件由3块层合板组成，材料为ZT7H/5429碳纤维增强树脂基复合材料，铺层顺序为[45/-45/0/0/45/90/-45/0/45/0/-45/90/45/0/-45/0/45/0/-45/0]s；螺栓为钛合金凸头高锁螺栓，其直径为8 mm，预紧力为5 N·m。层合板和螺栓材料参数如表1所示。

在CSS-88100电子万能试验机上进行拉伸试验；采用DH3820Net静态应变测试系统采集应变数据；采用双侧引伸计测量中间和两侧层合板的相对位移，标距段长度为100 mm，标距段位置如图1(a)所示。测量所得编号为E5-1和E5-2试件的载荷-位移曲线和修正后的载荷-位移曲线如图1(b)所示。

图1(b)中实线绘制的测量曲线具有明显的分段性，分别对应不同的传载模式。E5-1曲线在A点之前是静摩擦界面传载参与的混合传载阶段，A-B段为螺栓和动摩擦传载阶段，B点之后是层合板损伤阶段。为排除静摩擦界面传载的干扰，取线性A-B段斜率反推理想螺栓传载模式下的载荷-位移曲线，在图1(b)中以虚线表示。试验中通过采集钉间层合板中部的拉伸应变，结合层合板面内拉伸刚度计算各段钉间层合板的拉伸载荷，依次相减获得螺栓连接载荷及其比例，测量所得编号为1#、2#和3#螺栓的钉载比例依次为39.70%、29.48%和30.82%。

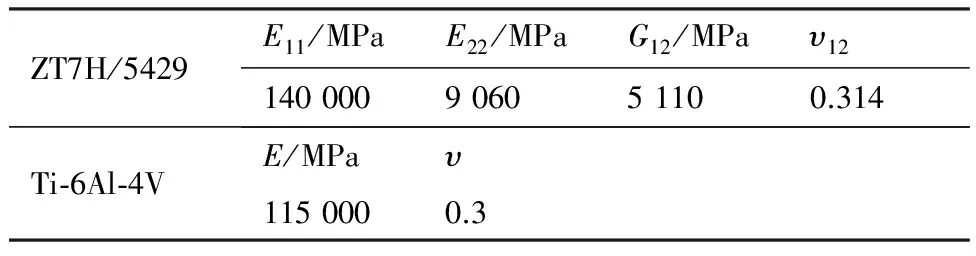
表1 层合板和螺栓材料参数Table 1 Material properties of laminate and bolt

1.2 单钉连接紧固件连接柔度试验测定

单钉连接的紧固件连接柔度试验测定采用图2(a)所示的双搭接试件，试件中螺栓、层合板材料和铺层参数与3钉连接试件相同，测量所得编号为D6-3和D6-4试件的载荷-位移曲线和修正后的载荷-位移曲线如图2(b)所示。依据修正后的载荷-位移曲线，计算连接点相对位移的公式为

(2)

式中：P为拉伸载荷；δe为引伸计标距段的拉伸位移；L1和L2为中间板和外侧板引伸计标距点与孔中心的距离；W1、t1和E1为中间板的宽度、厚度和拉伸刚度；W2、t2和E2为外侧板的宽度、厚度和拉伸刚度。将计算所得δ和试验测量的P值代入式(1)，即可求出单钉连接紧固件连接柔度，均值为7.43×10-6mm/N。

1.3 多钉连接紧固件连接柔度的理论解

模型的受力平衡方程组为

Kx=p

(3)

式中：p=[0,0,0,0,0,0,Pload]T为节点载荷向量；K为刚度矩阵；x为节点位移向量。对式(3)解析求解可得钉载计算公式为

(4)

(5)

(6)

2KB1KB3+KB2KB3)+9KB1KB2KB3

(7)

(8)

式中：Pi -j、Li -j和Ki -j为节点i和j之间层合板载荷、长度和拉伸刚度。

1.4 连接区钉载的有限元计算

钉载比例是计算多钉连接紧固件连接柔度理论解的必要条件，可以采用试验测量或有限元计算的方法得到。在ABAQUS中建立1列3钉连接件有限元模型如图4(a)所示。

模型中层合板和螺栓均由8节点三维实体缩减积分单元(C3D8R)组成；模型右侧固支，左侧施加拉伸位移载荷；层合板与层合板、层合板与螺栓的配合面设置有限滑移接触边界条件[21]，采用HT-1000高温摩擦磨损试验机测量层合板间动摩擦系数为0.42，螺栓预紧力施加位置如图4(a)所示。采用Standard求解器计算标距段拉伸位移和拉伸载荷，所得载荷-位移曲线与修正的试验曲线对比如图4(b)所示，二者线性段吻合良好，说明三维有限元方法对于螺栓和动摩擦传载阶段的连接刚度分析具有准确性。

连接区载荷中93%为螺栓传载，7%为层合板界面动摩擦传载，以单钉接触力与3钉接触力之和的比值作为钉载比例，代入式(4)～式(6)后求出各排螺栓的紧固件连接柔度，如表2所示。计算所得各排螺栓的紧固件连接柔度均不相同，说明复合材料连接结构不满足Morris在金属连接结构中所采用的多排钉紧固件柔度相同的假设，且各排螺栓紧固件连接柔度与单钉试验测定的结果也不相同。

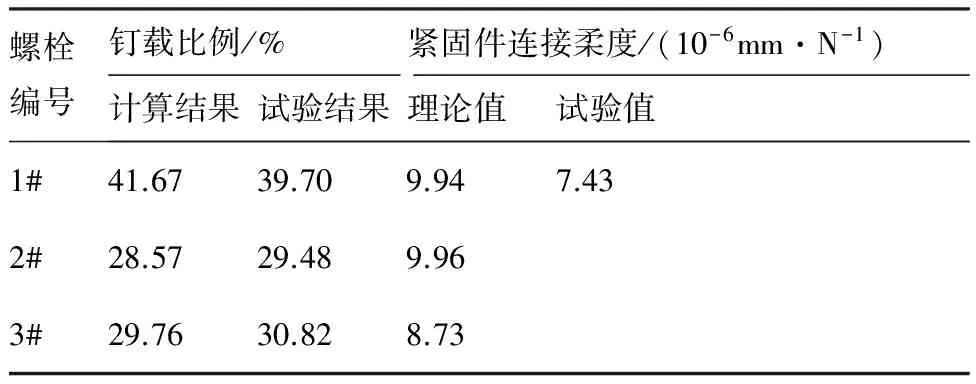
表2 紧固件连接柔度理论解Table 2 Theoretical results of fastener connection flexibility

导致各排螺栓紧固件连接柔度不相同的原因是：多排钉连接结构中层合板受钉载与旁路载荷联合作用，旁路载荷拉伸螺栓孔，导致螺栓杆和螺栓孔之间出现间隙，进而造成紧固件连接柔度变化。因此不宜直接使用由单钉连接试验所测定的紧固件连接柔度进行多钉连接结构钉载计算。

2 多钉连接中紧固件连接柔度的影响因素

2.1 旁路载荷对连接柔度的影响

采用图5所示的虚拟试件分析旁路载荷对紧固件连接柔度的影响。

模型由3块板搭接而成，载荷施加在中间板两端，P1、P2和P3分别是3块板的拉伸载荷。对于连接区B板，P2是旁路载荷，P1和P3之和为钉载。连接区附近的3块板设置为ZT7H/5429层合板，铺层参数和螺栓均与1列3钉试件相同。3块板中央设置为不同刚度的各向同性材料，由载荷按刚度分配原则可知，调整中部材料刚度可调控钉载和旁路载荷比例。

在ABAQUS中建立有限元模型，如图6(a)所示，选择Standard求解器。由于结构对称性，取一半结构建模并在对称面施加对称位移边界条件。

紧固件连接柔度按式(1)计算，其中，连接点相对位移的计算公式为

(9)

式中：P0和P1为标距段中A板L0段和L1段的拉伸载荷；P2为标距段中B板L2段的拉伸载荷；

δs为拉伸位移；L0+L1和L2分别为A板和B板的位移测量点与孔中心的距离；Wi、ti和Ei(i=0, 1, 2)分别为A板中L0段、L1段和B板中L2段的宽度、厚度和拉伸刚度。

定义B板中钉载和旁路载荷的比值为ξ，绘制紧固件连接柔度C*与ξ的关系如图6(b)所示。C*随着ξ减小而单调增大，当ξ趋于0时，C*为无穷大；当ξ趋近于无穷大时，C*趋近于常数，对应于单钉连接结构或多钉连接区首排钉的受载情况。当ξ>1.0时，C*变化较小，其增量<7%；但当ξ<0.5后，随着ξ的减小C*剧烈增加。对曲线进行数值拟合得到C*与ξ的函数关系式为

C*=a+bξ-1

(10)

式中：常数a的物理意义是无旁路载荷作用时的紧固件连接柔度，即单钉连接紧固件连接柔度。

B板中X1-X2段层合板的受力和变形情况与多钉连接区钉间层合板有相似性，图6(b)中也绘制了其等效拉伸柔度CL随ξ的变化曲线。层合板等效拉伸柔度定义为

(11)

式中：δ1-2为X1-X2段的拉伸位移；P1-2为X1-X2段的拉伸载荷。由图6可见，X1-X2段层合板的等效拉伸柔度与表征受力状态的ξ相关，且在ξ∈(0,10)范围中近似线性变化，可表示为

(12)

2.2 钉间板建模方法对连接柔度取值的影响

连接结构钉载分析中，紧固件建模方法和钉间层合板建模方法直接影响钉载计算结果的准确性。当选定的钉间板模型与实际结构存在刚度偏差时，可以通过修正紧固件连接柔度消除其对钉载计算结果的影响，也意味着由不同分析模型推导而来的紧固件连接柔度理论值将受到分析模型各元素建模方法的影响。对于小钉间距连接区的弹簧-质量模型，由式(12)可知模拟钉间层合板的线性弹簧与实际构件的柔度偏差为βξ。提取弹簧-质量模型的代表性双钉组合如图7所示，图中CⅠ、CⅡ和PⅠ、PⅡ分别为上下板的拉伸柔度和拉伸载荷；Cb1、Cb2和Pb1、Pb2分别为两钉的紧固件连接柔度和钉载。

依据1点和4点的位移协调关系，可得

x1+Cb1Pb1+CⅡPⅡ=x1+CⅠPⅠ+Cb2Pb2

(13)

若上下板的拉伸柔度分别有ΔCⅠ和ΔCⅡ的偏差，为保证系统受力状态不变，则两钉紧固件柔度的修正量ΔCb1和ΔCb2应满足

ΔCb1Pb1+ΔCⅡPⅡ=ΔCⅠPⅠ+ΔCb2Pb2

(14)

钉间层合板柔度偏差对紧固件连接柔度取值的影响具有传递性，若第i排螺栓处层合板柔度有偏差，将影响其后所有螺栓的紧固件连接柔度。

3 多钉连接中紧固件连接柔度的修正公式

针对旁路载荷和分析模型柔度偏差对紧固件连接柔度取值的影响，建立紧固件连接柔度修正公式为

(15)

3.1 针对旁路载荷的紧固件连接柔度修正

1)旁路载荷引起的螺栓孔变形

旁路载荷引起的螺栓孔变形量(见图8(a))可由含填充孔的带孔板拉伸模型计算。定义孔变形系数为

(16)

式中：Qbypass为远场拉伸应力；ΔD为拉伸载荷作用下的孔径变形量。含直径为8 mm填充孔的ZT7H/5429层合板在0°/±45°/90°铺层比例分别为3/5/2、4/5/1、5/3/2和6/3/1时，宽径比(W/D)对填充孔变形系数Ch的影响如图8(b)所示。由于增加0°层比例使得层合板面内刚度增大，因而在相同的宽径比下，0°层比例越高的层合板，其孔变形系数越小。

图8(b)中4条曲线均可拟合为指数函数形式，即

(17)

2)等效间隙和含间隙的紧固件连接柔度

旁路载荷使圆形螺栓孔拉伸为椭圆孔，由椭圆孔的销钉挤压载荷-位移曲线可求出螺栓杆和螺栓孔间的等效间隙量δg，如图9(a)所示。采用修正系数α表示等效间隙量和孔变形量的关系，即

(18)

因螺栓杆和螺栓孔间存在间隙δg，当连接点的相对位移总量为δ时，螺栓实际传递载荷为

Pb=C0(δ-δg)

(19)

式中：C0为无旁路载荷时的紧固件连接柔度。将式(18)和式(19)代入式(1)可得旁路载荷伴随下的紧固件连接柔度为

(20)

式(20)与式(10)有相同的形式，利用式(20)计算图5模型的连接柔度，当C0取值和a相同时，计算所得C*与有限元结果对比如图9(b)所示。旁路载荷伴随下的紧固件连接柔度计算结果和有限元结果完全吻合，说明旁路载荷造成的配合间隙是导致紧固件连接柔度增大的根本原因。

3.2 面向分析模型的紧固件连接柔度修正

钉间层合板模拟元素的柔度偏差和所采用的建模技术相关，不同分析模型中紧固件连接柔度取值的修正量也不相同。

1)模型适应函数

本文采用模型适应函数定量描述钉间层合板模拟元素的柔度偏差。在弹簧-质量模型中，模拟钉间层合板的弹簧可选择式(21)所示的区间线性函数作为模型适应函数。

ΔCL=ψ(ξ)=βξξ∈(0,10)

(21)

模型适应函数应具有函数值在ξ=0时为0、ξ无穷大时趋近于常数、在局部区间中为凸函数的特征。本文在[0,10]区间统一采用式(22)所示的单参数模型适应函数。

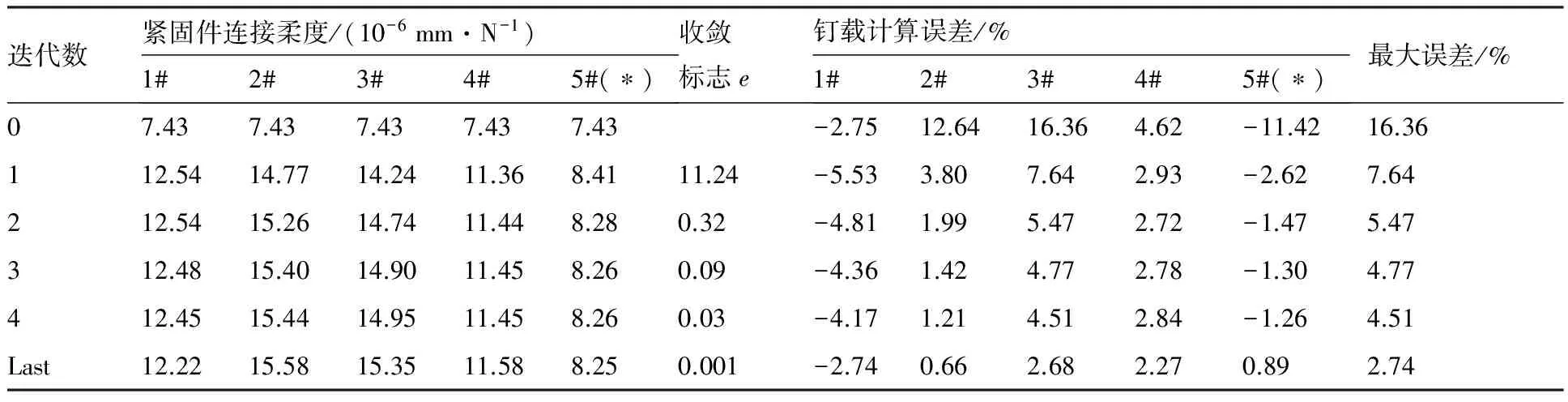
ψ(ξ)=βξn0

(22)

单参数模型适应函数的待定系数β可以通过双钉连接件拉伸试验进行标定。

2)模型适应函数的待定系数计算

采用图10(a)所示1列2钉连接试件进行未知系数计算，其层合板尺寸、材料、铺层和螺栓布局参数与3钉连接试件完全相同。

(23)

(24)

(25)

式中：Pout、ξout和Pinner、ξinner分别为双搭接结构中外侧板和中间板的拉伸载荷与钉载/旁路载荷比。为了消除引伸计测量误差对结果的影响，将式(25)两式相减求出模型适应函数的未知参数β。将模型适应函数代入式(26)可得针对分析模型偏差的紧固件柔度修正量。

(26)

式中：Pinner和Pout为第n排和第n-1排螺栓间两侧和中间层合板的拉伸载荷；(Pb)n为第n排螺栓的钉载。

3.3 修正模型的验证

对1列3钉连接结构按式(15)、式(20)和式(26)计算面向弹簧-质量模型的紧固件连接柔度，计算结果与解析结果的对比如表3所示。计算中，由试验测定的单钉连接紧固件连接柔度C0=7.43×10-6mm/N；模型适应函数选择为线性函数，系数β=7.48×10-7mm/N；填充孔变形系数Ch由层合板拉伸数值试验计算，其值为1.8×10-4mm/MPa；等效间隙的修正系数α由椭圆孔的销钉挤压模型计算，其值为0.6。

表3 1列3钉连接结构的紧固件连接柔度修正结果Table 3 Modified fastener connection flexibility results of one-line three-bolt joint

由修正公式计算所得紧固件连接柔度与理论结果吻合，采用修正后的紧固件连接柔度进行钉载计算，最大误差仅为0.2%，从而证明了多钉连接紧固件连接柔度修正公式的正确性。

4 紧固件连接柔度修正公式的应用

4.1 分析对象

从长桁传载的复合材料机身壁板对接区提取如图11(a)所示的1列5排螺栓连接件。上下板分别代表长桁对接角片和外搭接板，中间板代表长桁缘条，连接区螺栓及排距与3钉试件相同。采用工程上广泛使用的梁-壳有限元分析模型[22]计算钉载，在Patran中建立的钉载分析模型如图11(b)所示。模型中层合板用四节点壳单元(CQUAD4)模拟；螺栓紧固件由二节点梁单元(CBAR)模拟，截面惯性矩由连接柔度计算；模型左端固支，右侧施加2 mm的拉伸位移载荷。

4.2 钉载分配的迭代计算

由式(20)可知紧固件连接柔度与旁路载荷和钉载分配相关，若钉载未知，不能直接得到紧固件的连接柔度，因此需采用迭代算法进行紧固件柔度修正和钉载计算。对于壳元模拟的层合板，模型适应函数中n可取为0.5，按式(25)计算未知参数时，所需的双钉紧固件连接柔度理论值采用梁-壳有限元模型和遗传算法反演。钉载迭代计算过程如图12所示。

迭代计算中紧固件连接柔度的修正公式为式(15)，收敛条件为

(27)

4.3 计算结果分析

1)钉载计算结果

1列5钉连接结构的钉载迭代计算与三维有限元计算结果的对比列于表4中。

结果表明：对单钉紧固件连接柔度进行修正后，梁-壳模型的钉载计算结果与三维有限元计算结果吻合度提升显著，经过3次迭代，最大钉载计算误差小于5%，收敛时钉载计算结果的最大误差小于3%。特别地，该方法显著改善了钉载峰值的计算精度，最大误差由11%降低至2%以下，有利于连接强度的评估。

在计算时间方面，本文所建立的5钉连接结构三维有限元模型单元总数为448 920，计算时间超过20 h；而采用梁-壳模型单次计算时间为5 s，收敛时共耗时2 h，误差小于5%时仅用8 min，极大地提高了计算效率，且梁-壳模型的建模复杂度远小于三维有限元模型，还可避免含接触边界有限元计算的不收敛问题。

2)紧固件连接柔度与分析模型的相关性

使用弹簧-质量模型和不同网格密度的梁-壳有限元模型(见图11)，选择不同的模型适应函数对1列5钉连接结构进行钉载计算，模型适应函数对钉载计算结果和紧固件柔度的影响如表5所示。

结果表明：模型适应函数对钉载计算结果影响显著。对弹簧-质量模型效果较好的是线性函数，对梁-壳模型效果较好的是指数为0.5的幂函数。

表4 迭代过程中的1列5钉连接结构钉载计算结果Table 4 Calculation results of bolt load of one-line five-bolt joint in iterative process

注:(*)表示钉载峰值所对应的螺栓。

表5 模型适应函数对紧固件连接柔度的修正结果和钉载计算结果的影响

注：加粗的数字对应钉载计算误差最大值。

5 结 论

1) 复合材料层合板多钉连接结构中各排紧固件的连接柔度存在差异，直接使用单钉连接的紧固件连接柔度进行多钉连接钉载分析，将引起较大的计算误差。

2) 旁路载荷影响紧固件连接柔度的机理是对螺栓孔拉伸作用造成螺栓孔和螺栓杆之间的间隙。随着层合板钉载/旁路载荷比值ξ增大，紧固件连接柔度减小并趋近于单钉连接结构的紧固件连接柔度。

3)多钉连接结构中紧固件连接柔度的取值和建模方法相关，基于模型适应函数对紧固件连接柔度取值进行修正可以纠正分析模型偏差造成的钉载计算误差。

4)经过对多钉连接结构紧固件连接柔度的修正，弹簧-质量模型和梁-壳模型钉载计算的准确度显著提高。对于1列5钉连接结构，紧固件连接柔度修正前的钉载计算误差最大值大于16%，修正紧固件连接柔度后的钉载计算误差最大值小于3%，且计算效率高，适合大规模复合材料结构钉群连接区的应用。

参 考 文 献

[1] ZHOU Y H, HAMED Y N, CHI H, et al. A three dimensional implicit finite element damage model and its application to single-lap multi-bolt composite joints with variable clearance[J]. Composite Structures, 2015, 131(11): 1060-1072.

[2] GRAY P J, MCCARTHY C T. A global bolted joint model for finite element analysis of load distributions in multi-bolt composite joints[J]. Composites Part B—Engineering, 2010, 41(4): 317-325.

[3] 谢鸣九. 复合材料连接[M]. 上海： 上海交通大学出版社, 2011: 172-173.

XIE M J. Joints for composites materials[M]. Shanghai: Shanghai Jiao Tong University Press, 2011: 172-173 (in Chinese).

[4] TATE M B, ROSENFELD S J. Preliminary investigation of the loads carried by individual bolts in bolted joints: NACA TN-10511[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1946.

[5] NELSON W D, BUNIN B L, HART-SMITH L J. Critical joints in large composite aircraft structure: NASA CR-3710[R]. Washington, D.C.: NASA, 1983.

[6] SWIFT T. Fracture analysis of stiffened structure: ASTM STP842[S]∥Damage Tolerance of Metallic Structures: Analysis Methods and Application. West Conshohocken, PA: ASTM, 1984: 69-107.

[7] HUTH H. Influence of the fastener flexibility on the prediction of load transfer and fatigue life for multi-row joints: ASTM STP927[S]∥Fatigue in Mechanically Fastened Composite and Metallic Joints. West Conshohocken, PA: ASTM, 1986: 221-250.

[8] XIONG Y. An analytical method for failure prediction of multi-fastener composite joints[J]. International Journal of Solids and Structures, 1996, 33(29): 4395-4409.

[9] 舒怀， 李亚智， 刘向东. 紧固件连接柔度的解析与试验研究[J]. 工程力学， 2013, 30(3): 470-475.

SHU H， LI Y Z， LIU X D. Investigations on the fastener flexibility in mechanically fastened joints[J]. Engineering Mechanics, 2013, 30(3): 470-475 (in Chinese).

[10] SIONG B. Fastener flexibility in composite joints for aerospace structures[D]. Bedford: Cranfield University, 1998: 1-57.

[11] MCCARTHY M A, MCCARTHY C T, PADHI G S. A simple method for determining the effects of bolt-hole clearance on load distribution in single-column, multi-bolt composite joints[J]. Composite Structure, 2006, 73(1): 78-87.

[12] MCCARTHY C T, GRAY P J. An analytical model for the prediction of load distribution in highly torqued multibolt composite joints[J]. Composite Structures, 2011, 93(2): 287-298.

[13] ALKATAN F, ANDRIAMAMPIANINA J. Flexibility of hybrid load transfer assemblies: Influence of tightening pre-stress[J]. Aerospace Science and Technology, 2013, 25(1): 84-92.

[14] ANDRIAMAMPIANINA J, ALKATAN F. Determining load distribution between the different rows of fasteners of a hybrid load transfer bolted joint assembly[J]. Aerospace Science and Technology, 2012, 23(1): 312-320.

[15] 谢宗蕻, 李想, 杨淋雅, 等. 基于弹簧质量模型的复合材料螺接修理载荷传递计算方法[J]. 航空学报, 2016, 37(12): 3742-3751.

XIE Z H, LI X, YANG L Y, et al. A calculation method for load transfer in bolted repair of composite laminates based on spring-mass mode[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(12): 3742-3751 (in Chinese).

[16] 谢宗蕻, 李想, 郭家平, 等．考虑间隙配合的复合材料钉载分配均匀化方法[J]. 复合材料学报， 2016, 30(4): 806-813.

XIE Z H, LI X, GUO J P, et al. Load distribution homogenization method of multi-bolt composite joint with consideration of bolt-hole clearance[J]. Acta Materiae Composite Sinica, 2016, 33(4): 806-813 (in Chinese).

[17] OLMEDO A, SANTIUSTE C, BARBERO E. An analytical model for predicting the stiffness and strength of pinned-joint composite laminates[J]. Composites Science and Technology, 2014, 90(1): 67-73.

[18] MCCARTHY C T, O’HIGGINS R M, FRIZZELL R M. A cubic spline implementation of non-linear shear behaviour in three-dimensional progressive damage models for composite laminates[J]. Composite Structures, 2010, 92(1): 173-181.

[19] SHAROS P A, EGAN B, MCCARTHY C T. An analytical model for strength prediction in multi-bolt composite joints at various loading rates[J]. Composite Structures, 2014, 116(1): 300-310.

[20] MORRIS G. Defining a standard formula and test-method for fastener flexibility in lap-joints[D]. Delft: Delft University of Technology, 2004: 1-50.

[21] 侯赤. 空天飞机机体复合材料机械连接结构损伤与强度分析[D]. 西安: 西北工业大学, 2010: 56-61.

HOU C. Failure and strength analysis of composite mechanically fastened joints in space plane body-structures[D]. Xi’an: Northwestern Polytechnical University, 2010: 56-61 (in Chinese).

[22] RUTMAN A, IISOREANU A, JOHN A. Fasteners modeling for MSC. Nastran finite element analysis: AIAA-2000-01-5585[R]. Reston, VA: AIAA, 2000.