平面2R机械臂运动学分析

黄　健，李占贤

(华北理工大学 河北省工业机器人产业技术研究院，河北　唐山　063210)

0　引言

在实际工程领域,很多应用场合下不总是需要多自由度机器人的复杂运动,因此自由度少、结构简单、经济实用的串联机构早已引起国内外研究者的浓厚兴趣。随着科技的进步,人们涉足的领域越来越广,这就必然要求我们对知识和理论不断进行创新[1]。目前，机器人的运动学分析有两个问题需要解决:运动学正问题,即根据关节位移、速度、加速度和臂长求末端点的运动状态；动力学逆问题,即已知末端点运动轨迹和臂长求解对应的关节位移、速度和加速度[2]。平面2R串联机械臂的运动学分析至关重要，它可以为多自由度的复杂结构机器人的运动学分析、动力学分析、轨迹规划和控制方法的研究提供理论基础。

1　平面2R机械臂结构

平面2R机械臂主要由基座、大臂和小臂组成。基座固定不动，它的作用是固定机械臂，保持整个机械臂稳定。大臂是通过大臂关节和底座连接的，它们之间构成转动副。小臂是通过小臂关节和大臂连接的，它们之间构成转动副，小臂末端通常会和手爪连接，整个机械臂在平面内有两个自由度[3]。平面2R机械臂结构如图1所示。

2　平面2R机械臂的运动学正解

将平面2R机械臂机构简化为数学模型并建立坐标系，如图2所示。

图2中，θ1和θ2均为矢量，规定逆时针方向为正，顺时针方向为负。θ1>0为逆时针方向，θ2<0为顺时针方向。

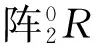
(1)

式(1)可以看成是坐标旋转和坐标平移的复合变换。

将复合变换写成矩阵形式：

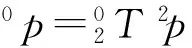
(2)

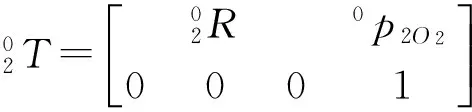
依据Denavit-Htenberg法，用4×4的齐次变换矩阵描述相邻两连杆的空间关系，得到平面2R机械臂的连杆参数，如表1所示。

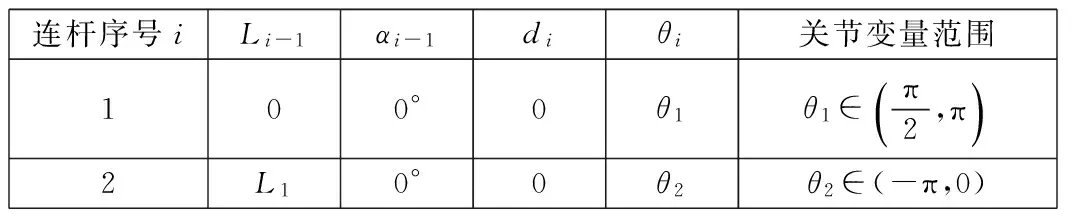
表1　平面2R机械臂的连杆参数

表1中，Li-1表示连杆i-1的长度；αi-1表示连杆i-1的扭角；di表示Li-1与轴线i的交点到Li与轴线i的交点的距离，沿轴线i测量；θi表示Li-1与Li之间的夹角，绕轴线i由Li-1到Li测量。

根据表1中的参数，可得到连杆变换矩阵：

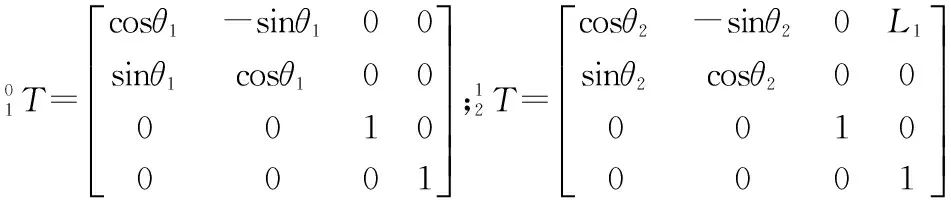
根据变换矩阵的乘法公式可知：

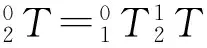
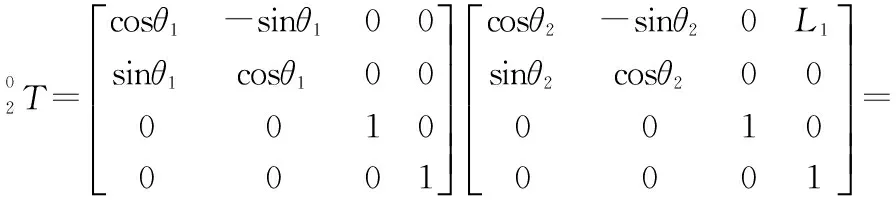
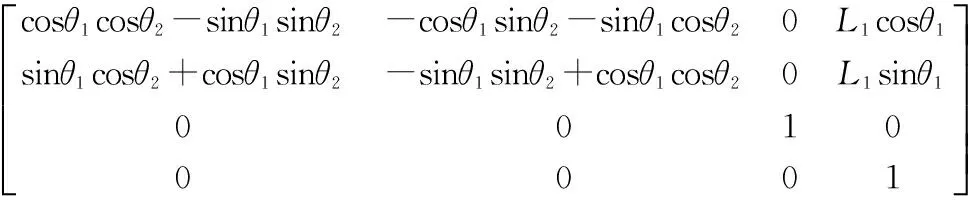
根据图1可知：

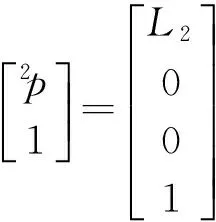
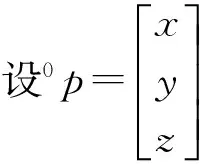
解得:

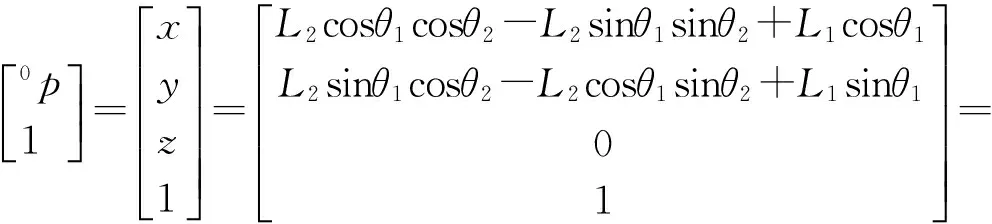
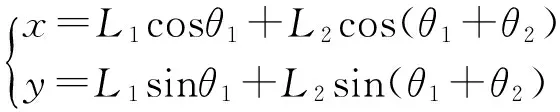
(3)

式(3)称为平面2R机械手的运动学方程。

3　运动学逆解

3.1　关节角度逆解

末端点坐标与杆长的三角形几何关系如图3所示。图3中-π-θ2<0为顺时针方向。

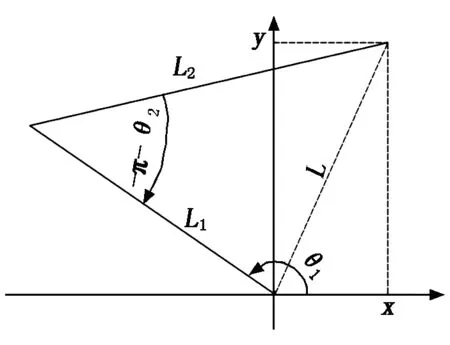
图3　三角形几何关系

由余弦定理可知：

解得:

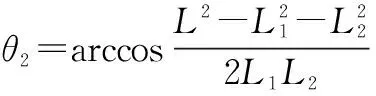
(4)

将L2=x2+y2代入式(4)中，得：

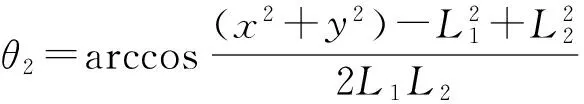
或

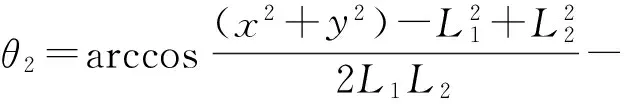
工程实际当中，多数情况下取θ2∈(-π，0)，则：

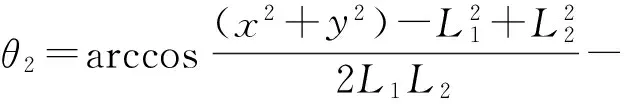
(5)

将式(5)代入式(3)中，得：

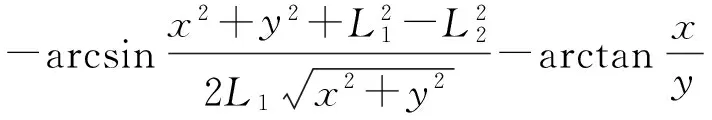
综上所述，求得θ1和θ2为：

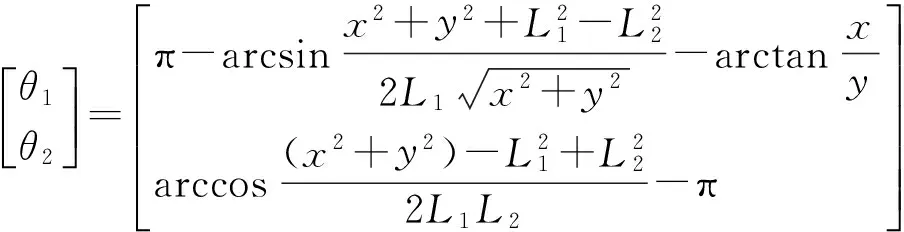
3.2　关节角速度逆解

操作臂的雅克比矩阵定义为它的操作速度与关节速度的线性变换，可以看成是从关节空间向操作空间运动速度的传动比。操作臂的运动方程为：

x=x(q).

(6)

式(6)代表操作空间x与关节空间q之间的位移关系。将式(6)两边对时间求导，即可得出q与x的微分关系：

x′=J(q)q′.

(7)

其中：x′称为末端操作空间的广义速度；q′为关节速度；J(q)是偏导数矩阵，称为操作臂的雅克比矩阵[4]。

将平面2R机械臂运动学方程两边同时对时间求一阶导数，则得：

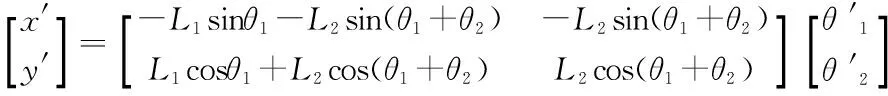
(8)

根据式(8)可以看出雅克比矩阵为：

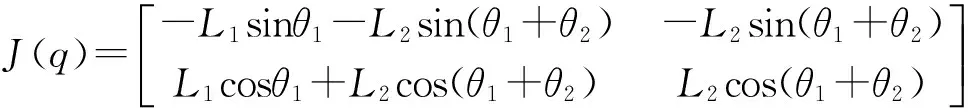
则雅克比矩阵的逆矩阵为：

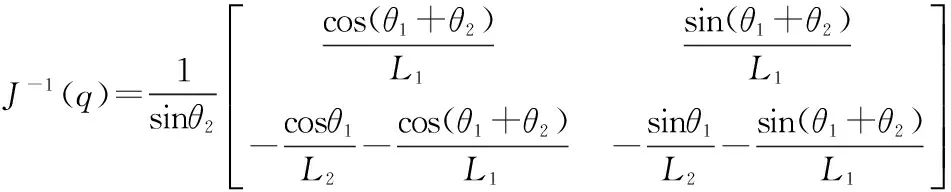
求得关节速度逆解为：

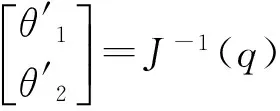
解得:

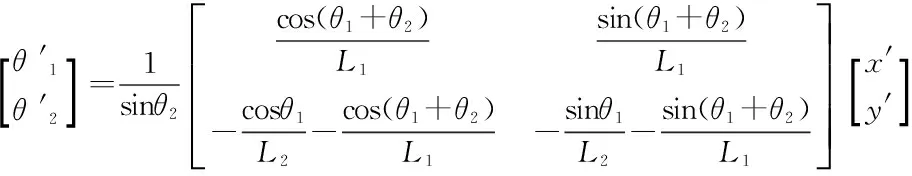
4　结语

平面2R机械臂的运动学正解表明末端点的位姿取决于大小臂长和大小臂关节角度，当臂长确定时，适当改变关节角度可以使末端点到达设定位置；运动学逆解表明关节角度、关节角速度和大小臂长以及末端点的运动状态有关，当臂长一定，末端点运动轨迹确定时，在某时刻的角度和角速度是确定值，此时机械臂有确定的位置。通过对机械臂运动学正逆解的分析可以很容易控制机械臂运动参数,使其达到预定位置来满足工作和使用要求。

参考文献：

[1]张磊.平面2R串联机器人机构运动学分析[J].科技创新导报，2009(25):32-33．

[2]李朝晖，李立.平面2R机器人机构混沌运动的控制[J].西南交通大学学报，2006,41(1):11-14.

[3]杨廷力.机器人机构拓扑结构学[M].北京: 机械工业出版社，2004.

[4]黄真，赵永生，赵铁石.高等空间机构学[M].北京: 高等教育出版社，2006.