基于三点法的主轴回转精度实验分析
张根明
(广东工业大学,广东 广州 511400)
0 引言
在超精密机床上加工回转体工件时,回转运动是它们最基本的运动形式。回转运动不管出现任何的误差都会直接反映在被加工件上。当我们进行超精密加工时,对加工表面误差影响最大的就是主轴的回转误差[1],因此对超精密机床回转误差的研究已经成为学者们关注的热点问题。
主轴回转误差指的是主轴的回转轴线与理想的回转轴线之间的误差[2]。研究主轴的回转误差能够很直观地看出主轴的动态性能以及将要被加工的工件表面的粗糙度以及形状误差。主轴的回转误差从空间上可划分为轴向误差、径向误差、斜向误差3种。
近几年,国内外有许多关于主轴回转误差测量技术研究的报道,Donaldson提出了用反转法误差分离技术来测量主轴回转误差[3]。东京技术学院Shoji Noguchi Tadao Tsukada和Atsushi Sakamot使用呈90°分布的两个传感器对数据进行读取,运用矢量法来显示主轴径向误差的测量结果,这种方法与传统方法相比较更为精确[4]。中国船舶工业公司第6354所阐光萍使用了一种新的方法——双向转位法,对主轴径向误差进行测量[5]。本文采用三点误差分离法有效地将传感器的安装误差和标准球的圆度误差从采集的数据中进行分离,并且对测量的数据进行详细分析,找出回转精度的影响因素。
1 测量系统原理及实验方案
1.1 测试系统原理
当主轴做匀速运动时,传感器探头对主轴进行回转误差的测量,由于不方便直接对主轴进行测量,因此,我们需要借助一个高精度的标准球来测量,标准球由真空吸盘吸附在主轴端面,如图1所示。在测量时会存在3种误差,分别为安装偏心误差、标准球的圆度误差和主轴的回转误差。第一种误差是由安装偏差引起的,可以转换为距圆心的距离的正弦值和余弦值,是一次函数,因此可用一次谐波滤除,剩余的两种误差可用误差分离算法进行分离[6-7]。因为主轴的回转误差与主轴的轮廓没有关系,是机器的固有特性,而标准球的形状误差也是固有特性,不会因测量装置而改变,因此这两个信号是独立的[8],我们采用三点法,将3个高灵敏的传感器布置在标准球同一截面,当主轴转动时,标准球跟着旋转,这时传感器采集数据,之后对采集的数据进行分离。图2为气浮主轴回转误差测量实物图。
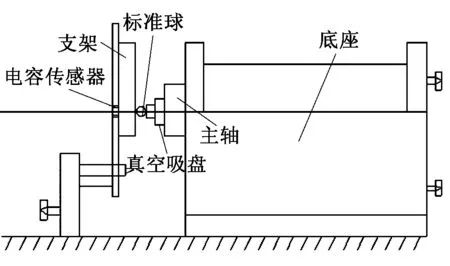
图1 气浮主轴回转误差测量装置示意图
1.2 实验方案
在主轴的轴端用真空吸盘吸附纳米级圆度的标准球,配套3探头安装底座,将3个非接触的双灵敏度电容位移传感器(传感器型号为CPL190、灵敏度0.389 V/um)按照一定的角度安装在同一截面内,将传感器采集到的数据导入电脑中,通过电脑写入的公式将电信号转化成位移值,最后再利用MATLAB程序进行仿真运算,将仿真后的结果绘制成图形。
分析径向误差中的同步误差(Synch)和异步误差(Asynch)两个指标。同步误差是指主轴连续转动时每一圈采样值的总和再除以转动的圈数,其来源于轴承与轴承座的位置安装误差,导致工件的圆度问题。异步误差是指每圈采样的极值减去每圈采样的同步误差再取最大值,其来源于主轴受到的不正当载荷引起的结构振动,导致工件表面光洁度问题。同步误差指标适用于分析刀具在主轴内旋转的铣、镗、钻等对圆度要求高的工艺,异步误差指标适用于车削、磨削等刀具与工件有间断的接触、对表面粗糙度要求高的工艺。
2 三点法误差分离模型
三点法误差分离技术是由日本学者青木保雄和大园成夫在1966年提出的,该方法利用频谱技术将圆度误差与回转误差分离开来。
图3为三点法分离圆度误差和回转误差的原理图,以传感器检测轴线S2、S3、S4的交点O为坐标原点建立平面直角坐标系XOY。R(θ)为被测件在θ处的圆度误差,X(θ)、Y(θ)分别为主轴在θ处的回转误差在X、Y轴上的分量。α、β分别为S3、S2与S4之间夹角[9]。
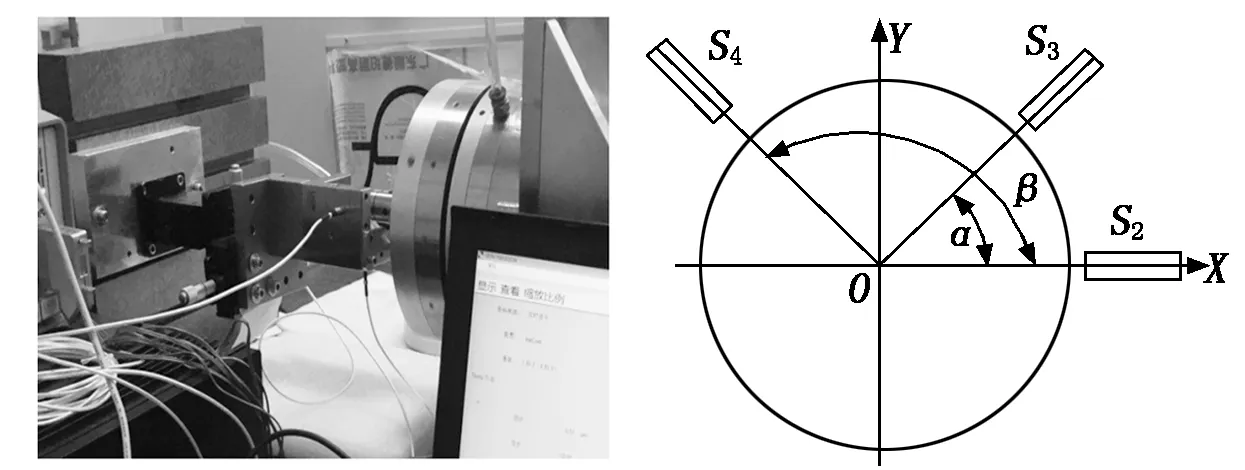
图2气浮主轴回转误差测量实物图图3三点法分离误差原理图
测量时,传感器被固定在支架上,标准球随着主轴做回转运动,其中S2(θ)、S3(θ)、S4(θ)分别为3个传感器的信号输出,这样可以得出三个传感器所包含的数据:
S2(θ)=R(θ)+X(θ).
(1)
S3(θ)=R(θ+α)+X(θ)cosα+Y(θ)sinα.
(2)
S4(θ)=R(θ+β)+X(θ)cosβ+Y(θ)sinβ.
(3)
引入传感器标定系数C2、C3、C4,则式(1)、式(2)、式(3)分别乘以C2、C3、C4得到:
C(θ)=C2S2(θ)+C3S3(θ)+C4S4(θ).
(4)
将X(θ)、Y(θ)消去,得到三点误差分离的基本方程:
C2S2(θ)+C3S3(θ)+C4S4(θ)=C2R(θ)+C3R(θ+α)+C4R(θ+β).
(5)
令C2=1,得到一组特性解为:
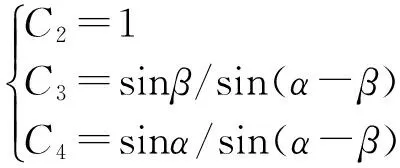
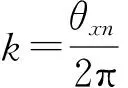
C(k)=C2S(k)+C3S(k1)+C4S(k2).
(6)
因为S(k)和C(k)均为周期序列,故对两边进行离散傅立叶变换,记C(k)的离散傅立叶变换为C(N),则:
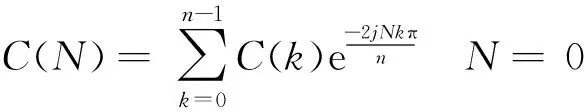
(7)
而对式(6)两端取DFT得:
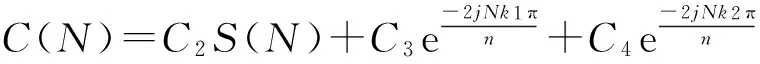
(8)
对式(8)取傅氏反变换,可求得形状轮廓误差:
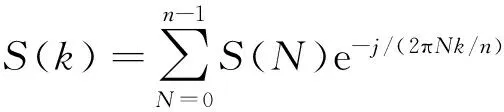
(9)
在超精密车床上,主轴运转时,其不断重复的转动并不是做周期运动,只是主轴回转时的精度非常高,几乎每转的保持性都非常好。由此计算出的同步误差可以视作主轴的回转运动误差:

(10)
Asyn(n)=S(k)-Syn(n).
(11)
3 测试数据分析
利用如图2所示的测量系统进行测量得到气浮主轴在(500~1 000)r/min转速下的径向误差。图4、图5分别为转速为500 r/min时的时域图、频域图。图6、图7为转速1 000 r/min时的时域图、频域图。

图4 同步、异步误差时域图(n=500 r/min)

图5 同步、异步误差频域图(n=500 r/min)
时域图是用极坐标图表示的,所形成的图像是在主轴转动时由传感器对标准球每一圈采160个点,共采集了30圈的结果,每一小格代表的是0.5 μm。图4(图6)中,同步误差形成了一圈不规则的图形,它是由主轴转动时一圈圈的数据值重叠形成的,其极大值点和极小值点的差值的一半代表同步误差的值。围绕在同步误差周围那些杂乱无章的点所围成的不规则图形代表异步误差,在图形中的任意角度找到最大值和最小值,它们的差值就是异步误差的取值,选取其中的最大值作为我们测量得到的异步误差。
在图5(图7)中,横坐标为测量时信号提取的信号阶次,其基频的单位为64 kHz;纵坐标代表的是每个阶次所对应的峰值,单位为mm。数字1代表1阶谐波,也就是基频,数字2~16代表2~16阶谐波,它们都是1的整数倍,因此都是同步误差,而那些分布在1~16中间的与基频成非整数倍关系的谐波都是异步误差。标准球的安装误差全部混在一次谐波中,因此我们要将其滤除掉。当2~16任何一个阶次的信号异常凸起,代表这个阶次的信号很差,则在图4中同步误差会出现相应数量的花瓣形状,同样它在最后计算同步误差时所占的权重也会很大,这样在计算中将会导致同步误差很大。
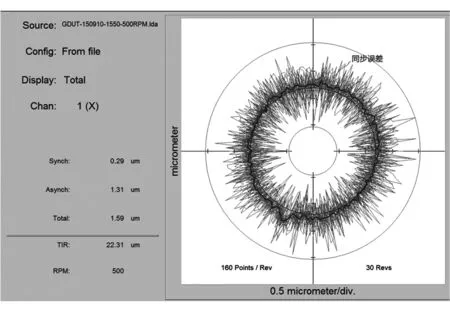
图6 同步、异步误差时域图(n=1 000 r/min)
为了方便、形象地将所测得的数据表示出来并且验证三点法误差分离的准确性,将所测得的原始数据提取出来,除去安装偏心和圆度误差,在XY方向上合成,进行计算处理,利用MATLAB对这些数据进行仿真得到回转误差的图像,这是主轴回转误差最常用的一种评定方法,不同转速下回转误差仿真结果如图8所示。
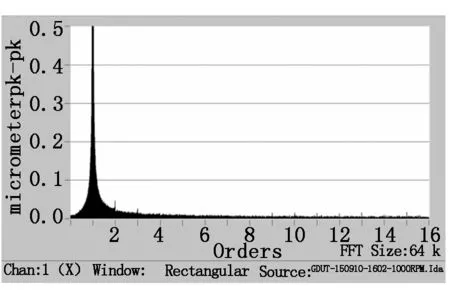
图7 同步、异步误差频域图(n=1 000 r/min)
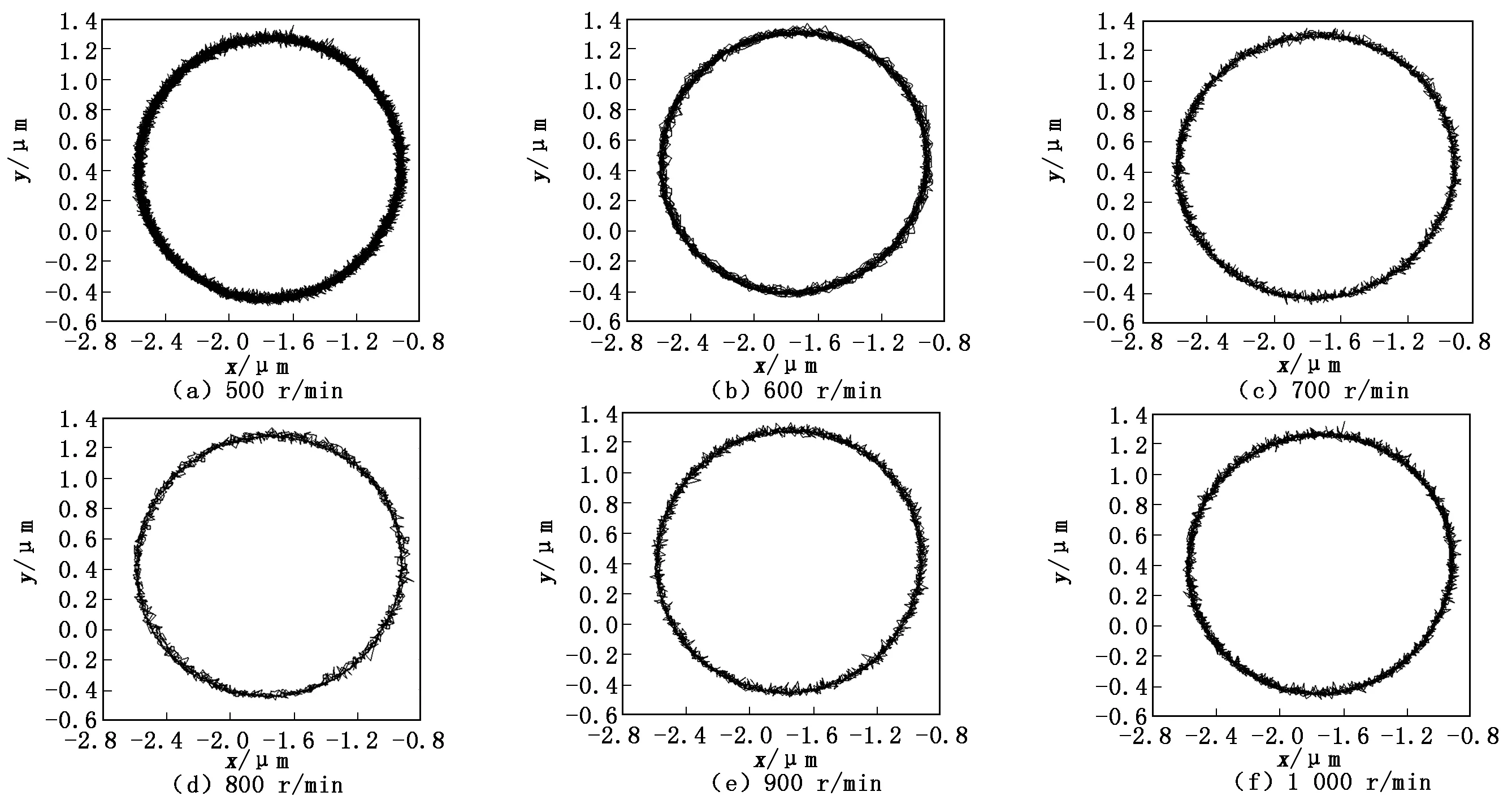
图8 不同转速下主轴的回转误差测量结果
图8表示的是所采集原始数据的二维仿真图形,图中任意一点所取横坐标或纵坐标的最大差值就是回转误差的值。
4 结语
本文通过三点法对气浮主轴回转误差中的同步误差、异步误差进行详细的测量、分析,并用MATLAB对不同转速下的同步误差和异步误差进行仿真,可以很好地预测主轴加工出来的工件圆度、表面粗糙度等各项指标,这为在线监控气浮主轴的回转误差提供了很好的理论依据。
参考文献:
[1]尹自强.超精密直线度测量及表面微观形貌分析研究[D].长沙:国防科技大学,2003 :1-10.
[2]陈长浩.主轴运动精度的测试与研究[D].北京:北京工业大学,2010:10.
[3]Donaldson R.A simple method for separating spindle error from test ball roundness error[J].Annals of the CIRP,1972,21(1):125-126.
[4]Shoji Noguchi,Tadao Tsukada,Atsushi Sakamot.Evaluation method to determine radial accuracy of high-precision rotating spindle units[J].Precision Engineering,1995,17(4):266-273.
[5]阐光萍.超精密空气主轴回转精度的测量与数据处理[J].航空精密制造技术,1999(1):5-7.
[6]Muralikrishnan B,Venkatachalam S,Raja J,et al.A note on the three-point method for roundness measurement[J].Precision Engineering,2005,29(2):257-260.
[7]洪迈生,蔡萍.多步法误差分离技术的比较分析[J].上海交通大学学报,2004,38(6):877-881.
[8]Liu H L.A new method and instrument for measuring circular motion error of NC machine tools[J].International Journal of Machine Manufacture,2005,45(11): 1347-1351.
[9]黄斌.基于激光位移传感器的数控机床主轴径向运动误差测试方法研究[D].杭州:浙江大学,2008:37.

