两端固支梁振动能量收集器的结构设计及优化*

刘　兵，虞梦琳，谷　旺，孔祥新，崔　岩

(1.大连理工大学 精密与特种加工教育部重点实验室，辽宁　大连　116024； 2.大连理工大学 微纳米技术及系统辽宁省重点实验室，辽宁　大连　116024)

0　引言

目前公布的MEMS压电振动能量收集器以悬臂梁结构为主[1]。但悬臂梁式压电振动能量收集器的尺寸较小(毫米级)[2]，结构简单，对复杂的振动环境适应性较差，限制了其输出性能的提升[3]。针对悬臂梁的尺寸和结构的局限性，很多学者设计了新型结构的能量收集器，Cui Yan[4]等设计的能量收集器利用多副梁结构增强了梁感知振动的能力，提高了输出电压。Wen Zhiyu等[5]设计的能量收集器利用了共质量块的阵列式结构，有效地提高了输出电压。李如春等[6]设计的能量收集器利用之字形结构改变梁的振动特性，进而提高输出电压。现有文献鲜有对其他支撑梁结构的研究，两端固支梁结构不仅可以满足较大尺寸的设计，还可以很好地适应复杂的振动环境。

本文设计一种厘米级、两端固支梁压电振动能量收集器，对两端固支梁进行了力学分析，通过对比两端固支梁与悬臂梁结构的振动特性，导出了两种结构关于最大应力和固有频率的关系式，利用关系式确定了两端固支梁结构的优化方法，并将公式计算值与ANSYS软件的仿真值进行对比。

1　两端固支梁的结构设计及力学分析

1.1　结构设计

两端固支梁压电振动能量收集器的结构设计如图1所示。两端固支梁由基座、固支梁、上质量块、下质量块等组成。梁的横截面由6层材料组成。当基座感知振动时，固支梁随质量块振动，梁的上、下表面产生拉伸或压缩变形，PZT压电层随之发生正压电效应，实现机械能向电能的转化。

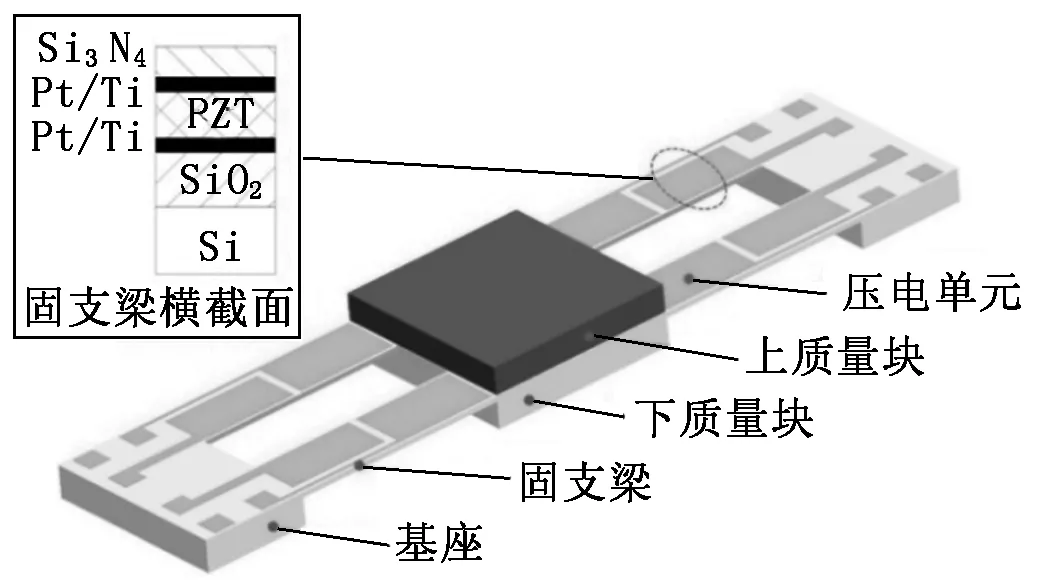
图1　两端固支梁压电振动能量收集器结构

1.2　力学分析

两端固支梁结构可简化为在质量块两侧受集中载荷的力学模型，如图2(a)所示，Fm为质量块重力的一半。由于两端固支梁左右对称，根据对称性原理，在小变形不考虑轴力的影响下，两端固支梁的一半可简化为悬臂梁，建立悬臂梁等效受力变形图，如图2(b)所示，自由端受集中载荷力F和弯矩Min共同作用，F和Min都作用在梁末端，x为梁的横截面距根部的距离，l为F的作用点距根部的长度，点A、点B和点C分别为梁的根部、末端和中点，点B′和点C′为梁变形后点B和点C的位置。梁截面为矩形，宽为b，厚为h。

对于悬臂梁结构而言，如图2(b)所示，根据边界条件，固定端A的转角和挠度均为零，在单独F作用下，任意横截面上的弯矩方程和挠曲线方程为：

M1=F(l-x).

(1)

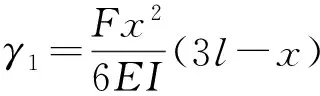
(2)

其中：E为梁的弹性模量；I为梁的横截面惯性矩,I=bh3/12。

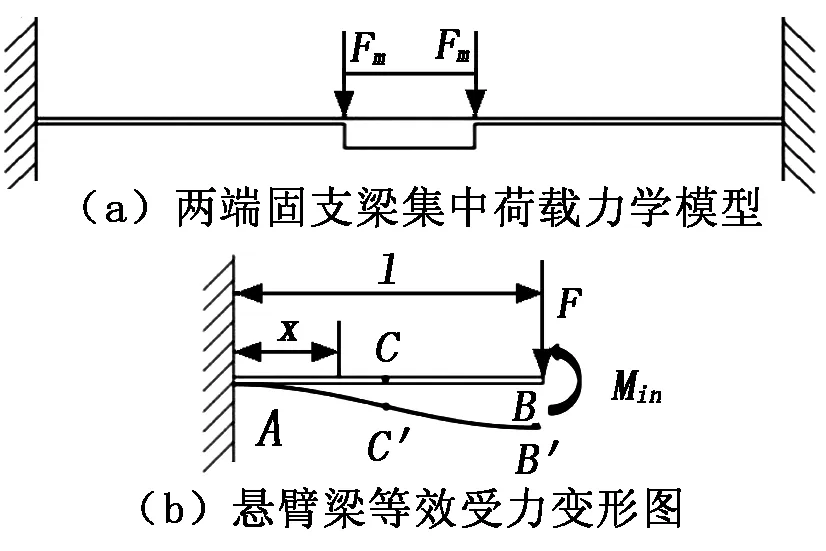
图2　两端固支梁力学分析模型

悬臂梁结构在单独Min作用下，任意横截面上的弯矩方程和挠曲线方程为：

Min=-Fl/2.

(3)

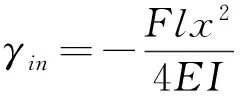
(4)

对于两端固支梁结构，可通过叠加法计算其任意横截面上的弯矩方程和挠曲线方程为：

M2=M1+Min=F(l-2x)/2.

(5)

γ2=γ1+γin=Fx2(3l-2x)/12EI.

(6)

通过式(6)的挠曲线方程可描述两端固支梁半边变形情况，如图2(b)中AC′B′所示，其中AC′段发生拉伸变形，在C′B′段发生压缩变形。

2　两种梁振动特性的对比分析

为了提升能量收集器的输出性能，要求能量收集器匹配环境中低频振源，并获得较大的应力来增强压电层的压电效应，这就要求所设计的梁结构同时获得较低的固有频率和较大的应力。悬臂梁和两端固支梁结构集中载荷力学模型如图3所示，x为梁的横截面距根部的距离。图3(a)中，F1为悬臂梁质量块m1的重力，F=m1g(g为重力加速度)，M1为梁距根部x处的弯矩，l1为F1的作用点距根部的长度。图3(b)中，F2为两端固支梁半边质量块m2的重力,F2=m2g，M2为梁距根部x处的弯矩，l2为F2的作用点距同侧根部的距离。其他尺寸和材料参数均相等。

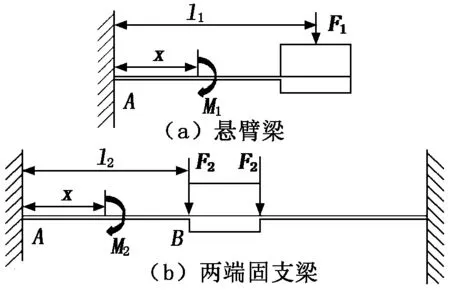
图3　两种结构的集中载荷力学模型

根据静位移法梁结构固有频率计算公式，对于一个单自由度系统，其固有频率为：

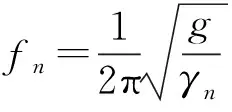
(7)

其中：γn为最大挠度。

将式(2)和式(6)分别代入式(7)，即得悬臂梁和两端固支梁结构的固有频率f1、f2：

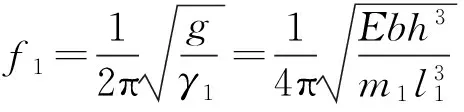
(8)

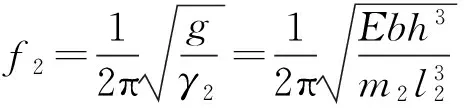
(9)

根据材料力学原理梁结构应力计算公式，梁上表面的应力σ为：

σn=Mny/I.

(10)

其中：Mn为弯矩；y为厚度的一半，y=h/2。

将式(1)和式(5)分别代入式(10)，即得悬臂梁结构的最大应力σ1和两端固支梁结构的最大应力σ2表达式：

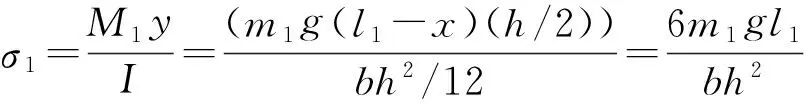
(11)

(12)

当m2=m1，l2=l1，且都为定值时，联立式(8)、式(9)、式(11)和式(12)得两种结构的最大应力和固有频率为：

2σ2=σ1=6m1gl1/(bh2).

(13)

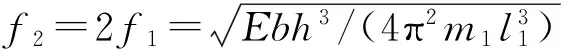
(14)

由式(13)和式(14)知，σ2为σ1的1/2倍，f2为f1的2倍，两端固支梁结构f2和σ2的取值都不利于能量收集器的输出性能的提升。

为了达到减小f2和增大σ2的效果，本文提出了以悬臂梁结构的σ1、f1作为基准，通过推导出的两种结构关于长度比Lp和质量比Mp的等应力和等频率公式，确定同时满足减小f2和增大σ2的区域。Lp和Mp无单位量纲。令m1和l1均为定值,则：

Lp=l2/l1.

(15)

Mp=m2/m1.

(16)

当f2=f1时，联立式(8)、式(9)、式(15)、式(16)，即得两种结构关于Lp和Mp的等频率公式：

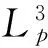
(17)

当σ2=σ1时，联立式(11)、式(12)、式(15)、式(16)，即得两种结构关于Lp和Mp的等应力公式：

Mp=2/Lp.

(18)

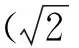
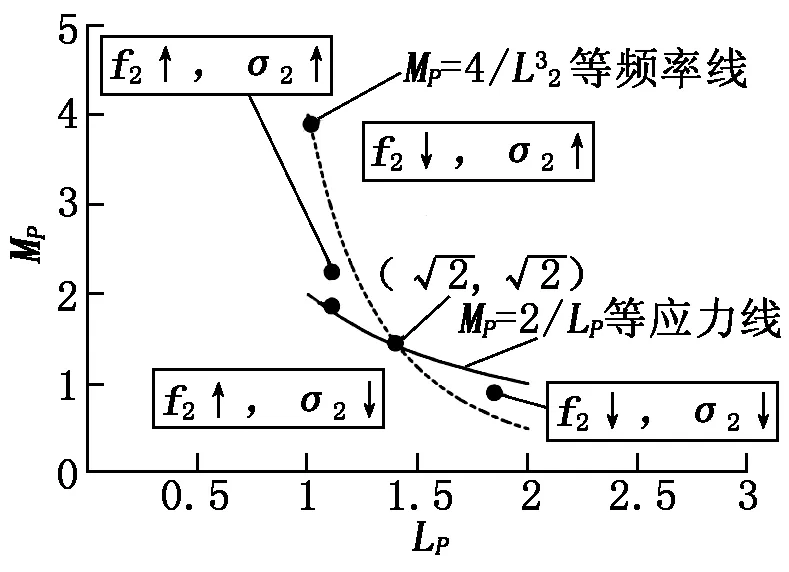
图4　等频率线和等应力线

3　仿真分析

利用ANSYS有限元仿真软件对悬臂梁和两端固支梁结构进行建模仿真，求解两种结构的最大应力和固有频率，并与两种结构的公式计算结果进行对比。根据图3和式(8)、式(9)、式(11)、式(12)的参数，对两种结构的尺寸进行设置，两种结构的尺寸如表1所示。两种结构质量块的参数如表2所示。

表1　两种结构的尺寸

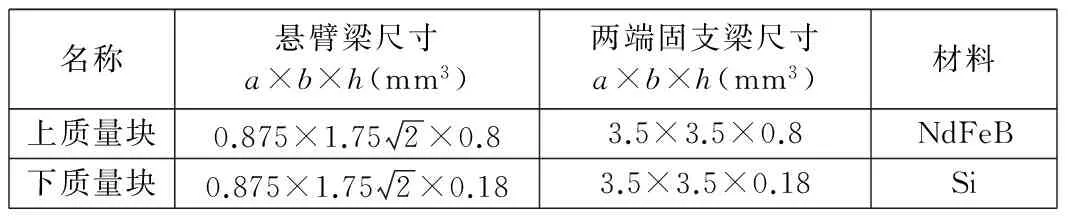
表2　两种结构质量块的参数

对上述两种结构的最大应力和固有频率进行仿真计算，结果如图5所示。仿真值、公式计算值和相对误差δ见表3。

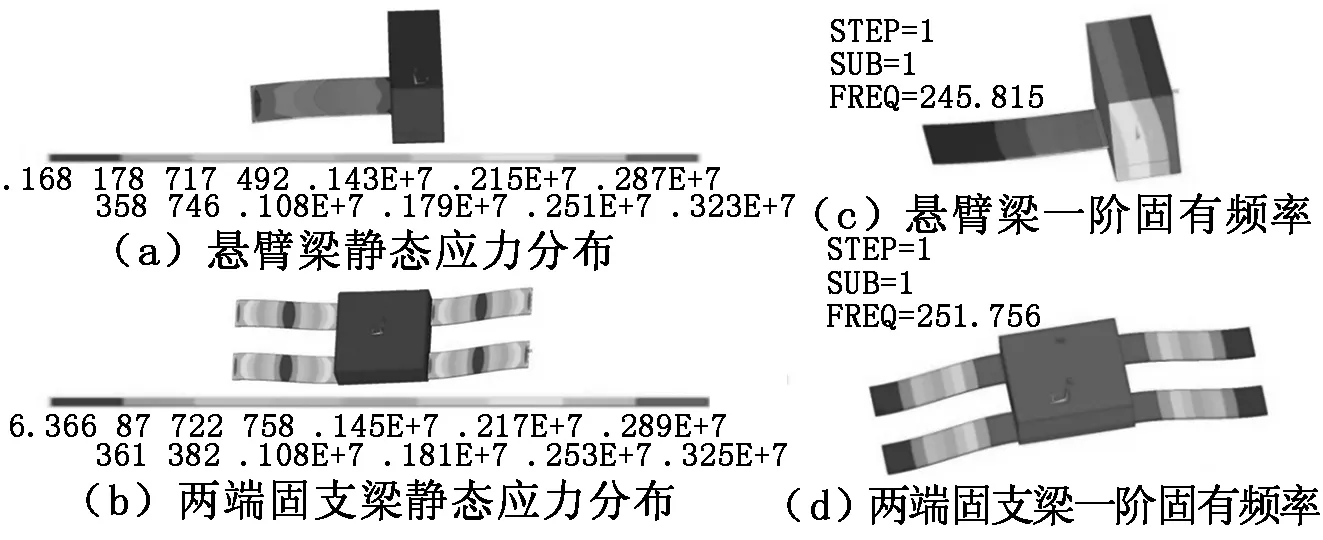
图5　两种结构应力和固有频率仿真结果

表3中列举了两种结构的最大应力仿真值σ仿真、最大应力公式计算值σ公式、固有频率仿真值f仿真、固有频率公式计算值f公式，计算了公式计算值相对于仿真值的相对误差δσ和δf，并计算了两端固支梁结构的仿真值、计算值相对于悬臂梁结构的相应数值的相对误差δ，其中δσ的最大值为0.92%、δf的最大值为1.79%，δ的最大值为2.42%，其他相对误差值均小于1%。通过计算值和仿真值相对误差对比，验证了关于f2、σ2优化方法的可行性，为两端固支梁结构的优化提供了指导。

表3　仿真结果、公式计算结果和相对误差δ数值表

4　结束语

本文对所设计的两端固支梁结构进行了力学分析，确定了梁的变形情况。对比两端固支梁与悬臂梁结构的振动特性，通过所推导的两种结构关于Lp和Mp的等应力和等频率公式，可以确定同时实现减小f2和增大σ2的区域。并利用ANSYS仿真对应力和等频率公式进行了验证。结果表明：公式计算值和仿真值相对误差低于2.42%，对f2、σ2优化有利于能量收集器输出性能的提升。

参考文献：

[1]刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势[J].振动与冲击，2012，31(16) : 169-176．

[2]Ma X K,Wilson A,Rahn C D,et al.Efficient energy harvesting using piezoelectric compliant mechanisms:theory and experiment[J].Journal of Vibration & Acoustics,2015,138(2):51-59.

[3]Shen Hui,Qiu Jin-hao,Ji Hong-li,et al.Alow-power circuit for piezoelectric vibration control by synchronized switching on voltage sources[J].Sensors and Actuators，2010,161:245-255.

[4]Cui Yan,Zhang Qunying，Yao Minglei,et al.Vibration piezoelectric energy harvester with multi-beam[J].Aip Advances,2015,5(4):4495-4498.

[5]Wen Zhiyu,Deng Licheng,Zhao Xingqiang,et al.Improving voltage output with PZT beam array for MEMS-based vibration energy harvester:theory and experiment[J].Microsystem Technologies,2015,21(2):331-339.

[6]李如春，征琦，施朝霞.微型之字形压电式能量收集器输出电压的建模和仿真[J].传感技术学报，2015,28(5)：629-634.