基于协同优化的民机DMC控制模型研究*

贾宝惠，吴　婧，卢　翔

(中国民航大学 航空工程学院，天津　300300)

0　引言

民用飞机的直接维修成本(Direct Maintenance Cost，简称DMC)是指在完成飞机的维修中直接花费的人工工时和材料的费用。维修成本是航空公司直接运营成本的重要组成部分，一般要占到10%～20%的比例。全寿命周期成本的70%在产品设计阶段已经决定，降低成本的机会为35%，同时降低成本的机会呈现逐渐下降趋势，所以研制阶段DMC的有效控制，对优化产品设计，以最低的维修成本维持产品固有的安全性、可靠性与维修性水平，具有决定性的作用[1]。

国外对研制阶段维修成本的分析主要适用于初步设计阶段，包括Liebeck方法、欧洲98方法、AEA2009方法和Harris方法[2-3]，它们将维修成本分为机体和发动机两个部分，Liebeck方法用于飞机构型优化分析，AEA2009广泛用于经济分析和构型优化，而Harris只适用于美国市场条件[4]。国内对维修成本的研究集中于DMC的分配、预计和评估，提出了相似分配法、功能分解法以及CBR-DMC目标值预测[5]等方法。综上，国内对详细设计阶段分配值和预计值的综合权衡只限于定性分析，对于如何将成本指标贯彻到设计中，实现面向成本的设计缺乏研究[6]。

本文针对民机研制阶段DMC控制问题，建立协同优化模型，对部件和系统的DMC分配值进行优化，通过定量计算优化可靠性、维修性参数，降低维修成本，提高产品的市场竞争力。

1　DMC控制问题分析

研制阶段，DMC控制包括整机目标值的确定、DMC的分配和DMC的预计。按维修级别将DMC分为原位维修成本和离位维修成本。由于供应商通常只对离位DMC提供担保，所以本文不考虑原位维修成本[7]。离位维修是指在车间内，对零部件或发动机进行测试、修理和翻修工作。本文在DMC分配值和预计值已知的基础上，将机体分为系统和部件两级，对其分配值和预计值进行综合权衡分析。DMC控制流程如图1所示。

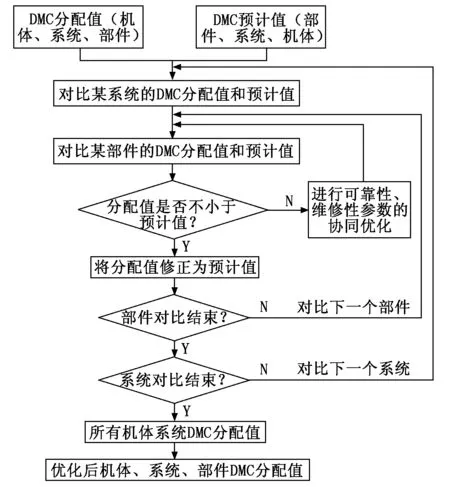
图1　DMC控制流程

由图1可知，将机体、系统、部件的DMC分配值和预计值作为输入，首先按各系统分配值由大到小的顺序进行系统级的对比分析，再依次对比该系统所包含的各部件的分配值和预计值(仍按照分配值由大到小的顺序)。对于某一部件，如果分配值不小于(大于或等于)预计值，将分配值修正为预计值；如果分配值小于预计值，建立协同优化模型，修正可靠性、维修性设计参数，重新进行权衡分析，直至所有部件、系统的分配值都大于或等于其预计值，输出优化后机体、系统和部件的DMC分配值。

2　DMC控制协同优化模型

协同优化方法是由Stanford大学的Kroo教授等人在一致性约束算法基础上提出的分布式、多级的优化方法。其主要思想是将复杂的工程系统设计问题分解为一个系统级和几个学科(子系统)级问题，每个学科同时进行分析和优化两个过程，然后采用某种策略来协调各学科的设计结果[8]。

协同优化的结构与现有工程设计分工的组织形式一致，各学科独立性强，收敛可靠，使得计算机网络实现异地协同设计优化成为可能。故本文采用协同优化模型对可靠性参数和维修性参数进行优化，为我国民用飞机的研究提供有价值的参考。

2.1　设计向量

DMC控制分为系统和部件两级，系统的维修成本由组成该系统的各部件维修成本累加而成，部件级DMC控制是所有工作的基础。综合考虑系统和部件维修成本估算方法，设计向量由三个设计参数构成：平均非计划拆卸间隔时间MTBUR(Mean Time Between Unscheduled Removals)、平均故障间隔时间MTBF(Mean Time Between Failures)和平均计划维修间隔MTPM(Mean Time Between Planned Maintenance)。设计向量可记为：

X={x1，x2，x3}={MTBUR，MTBF，MTPM}.

(1)

2.2　目标函数

部件的直接维修成本为：

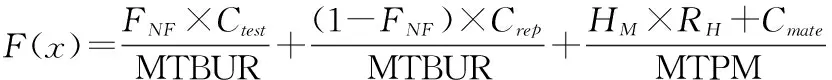
(2)

其中：FNF为部件的无故障发现率，且FNF=1-MTBUR/MTBF；Ctest为部件的测试成本，美元；Crep为部件的修理成本，美元；HM为人工时；RH为人工时费率，美元/人工时；Cmate为材料费，美元。

2.3　约束条件

假设MTBUR、MTBF、MTPM定义的最短时间分别为a、b、c飞行小时，则子系统级约束条件为：

(3)

综上，DMC最小的数学模型为：

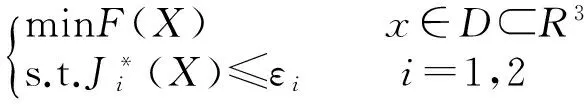
(4)

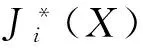
根据协同优化思想，构建民用飞机直接维修成本的协同优化计算框图，如图2所示，该框图包括一个系统级优化和可靠性、维修性两个学科级优化。

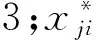
图2　协同优化计算框图

3　仿真研究

本文以ATA38水/废水系统为例，建立DMC控制协同优化模型，通过MATLAB进行仿真研究，优化该系统的DMC分配值。水/废水系统的分配值是0.973 3$/FH，预计值是0.961 6$/FH，各部件的DMC分配值和预计值如表1所示，RH=25$/FH。

表1　水/废水系统各部件的DMC分配值和预计值

按照分配值由大到小的顺序对各部件进行优化，对于分配值不小于预计值的10个部件(冲洗包1、厕所热水器5、逻辑控制模块6、空气过滤器10、手动隔离阀11、水位探测器12、高度开关13、便携式水箱14、减压阀15、废水箱组件16)将分配值修正为预计值；对于分配值小于预计值的7个部件(压缩机2、试剂注射泵3、厕所真空组件4、马达继电器7、废水状态面板8、水系统界面控制器9、带加热的冲洗接头17)建立可靠性、维修性协同优化模型，优化设计参数。

遗传算法适用于解决复杂的非线性和多维空间寻优问题，本文利用神经网络的非线性拟合能力和遗传算法的非线性寻优能力寻找函数极值。遗传算法进行优化无需求导或是其他信息，甚至不要求设计空间是连续的，而且具有较好的全局搜索性能，并能弥补系统级优化对初始点选取敏感和可能不收敛的缺点[10]。设定种群规模N=50，采用实数编码，定义交叉概率为0.4，变异概率为0.01，最大进化代数为100。

由MATLAB仿真得到优化过程中各部件最优个体适应度变化曲线，适应度表示输入值与最优值之间的差异。图3为废水状态面板适应度曲线。由图3可知，随着进化代数的增加，适应度逐渐降低，当适应度趋近于零时，所得结果即为最优解。优化后各部件分配值如表2所示，系统的DMC分配值为0.9421美元/FH，减小了0.0312美元/FH，多余的指标可以视情况分配给其他系统或部件。

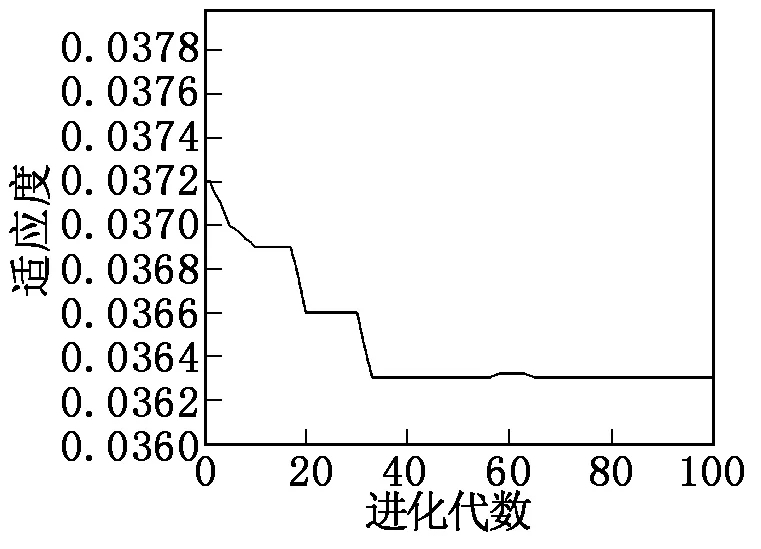
图3　废水状态面板适应度变化曲线

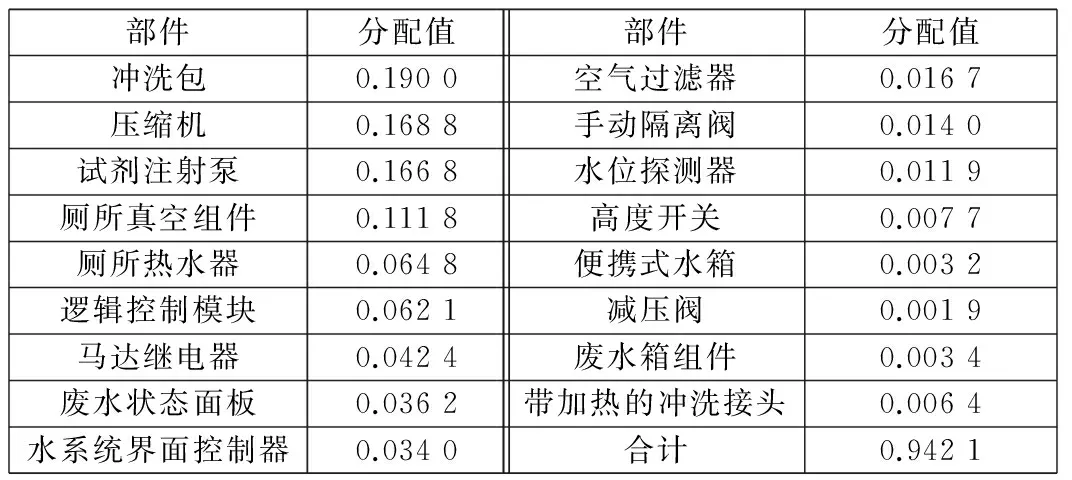
表2　优化后水/废水系统各部件DMC分配值 美元/FH

对比各部件分配值、预计值和优化后分配值，如图4所示。结果表明，改进的组合遗传算法均能实现可靠收敛，且收敛速度快，不受初始点影响。协同优化模型同时实现了可靠性参数和维修性参数的优化，优化结果在原值基础上上下浮动1%～3%，技术敏感度不高，不会产生设计上的技术难题，验证了模型的有效性。

4　结语

DMC是衡量民机经济性的一个重要指标，本文首先研究民机研制DMC控制流程，然后建立民机研制DMC控制协同优化模型，最后以ATA38水/废水系统为例进行MATLAB仿真研究，采用遗传算法编程求解最优解。改进的组合遗传算法能实现可靠收敛，且收敛速度快，不受初始点影响；协同优化模型同时实现了可靠性优化和维修性优化，优化结果变动小，技术敏感度不高，不会产生设计上的技术难题；该模型实现了维修成本的定量计算，为国产客机研制提供指导，也为运营阶段DMC的监控和全寿命周期维修成本的研究奠定了基础。

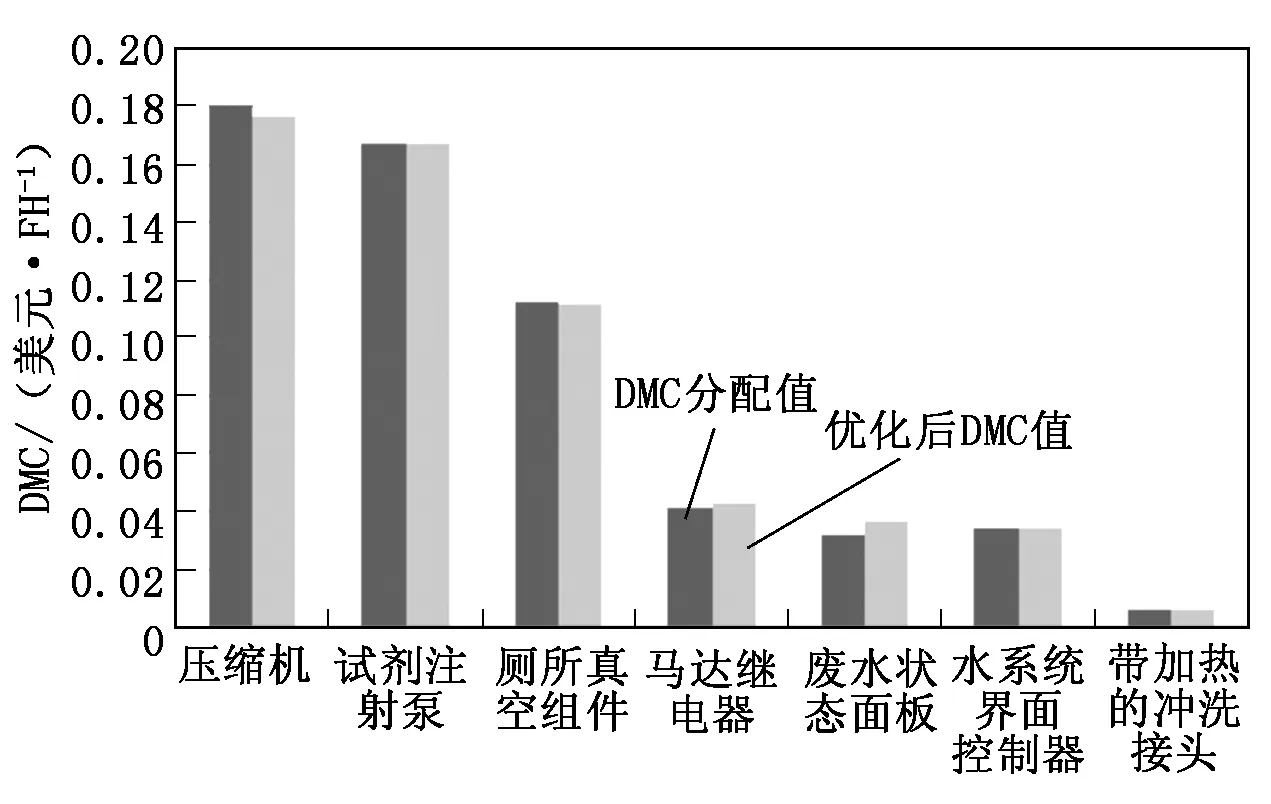
图4　优化前后DMC分配值对比分析图

参考文献：

[1]陈勇,吴静敏,左洪福.面向全寿命周期的民机直接维修成本分析和控制[J].航空维修与工程,2006(5):24-27.

[2]Wang H,Gao J,Wu H.Direct maintenance cost prediction of civil aircraft[J].Aircraft Engineering and Aerospace Technology,2014,86(5):406-414.

[3]Regattieri A,Giazzi A,Gamberi M,et al.An innovative method to optimize the maintenance policies in an aircraft:general framework and case study[J].Journal of Air Transport Management,2015,44:8-20.

[4]李晓勇,叶叶沛,李晨.商用喷气式飞机DMC分析模型应用研究[J].民用飞机设计与研究,2012(2):22-27.

[5]吴静敏.民用飞机全寿命维修成本控制与分析关键问题研究[D].南京:南京航空航天大学,2006:1-12.

[6]商桂娥，苏茂根.面向民用飞机设计的维修成本分析[C]//第六届中国航空学会青年科技论坛.北京：中国航空学会，2014：1754-1757.

[7]赵健,冯俊,邱小明.航空电子设备直接维修成本预计方法[J].航空计算技术,2014,44(2):22-25.

[8]周奇.多学科协同优化算法及其在船舶概念优化设计中的应用[D].北京：中国舰船研究院,2014：1-10.

[9]龚春林,谷良贤,袁建平.基于全局优化算法的多学科优化计算构架[J].西北工业大学学报,2009(1):52-56.

[10] 葛继科,邱玉辉,吴春明,等.遗传算法研究综述[J].计算机应用研究,2008,25(10):2911-2916.