逐步I型区间删失下Lomax分布形状参数的估计
龙沁怡,唐 俊
(内蒙古科技大学 理学院,内蒙古 包头 014010)
Lomax分布可视为由指数伽玛分布组合而成的混合分布,由于其分布形式类似于 Pareto分布,因此常常被称之为第二型的Pareto分布.在医学试验和工程科学等方面,大多数产品都具有单调递增或单调递减的失效率,这是产品的明显寿命特征,因此该分布在工程试验中占有重要地位. 迄今为止已经有很多统计学者研究了该分布的统计推断问题.文献[1-4]基于完全样本和删失样本,选取多种损失函数和先验分布得到了Lomax分布形状参数的贝叶斯估计.文献[5]研究了Lomax分布参数的极大似然估计,并推广到有缺失数据的两个Lomax分布总体中,证明了估计量的相合性和渐近正态性. 文献[6-7]讨论了Lomax分布参数的经验贝叶斯单边和双边检验,并证明了检验函数的渐近最优性.在产品的寿命检验和生存分析中经常会遇到删失样本,而逐步区间删失是逐步删失的一个推广,不仅可以节省试验成本还可以了解产品的失效机理,在寿命试验中经常被采用.文献[8] 基于逐步II型区间删失样本,运用Newton-Raphson算法研究了Pareto分布的参数估计和性质,证明了估计的相合性和渐近正态性.文献[9] 在逐步I型区间删失样本下,用EM算法确定参数的极大似然估计,并证明了极大似然估计的相合性和渐近正态性.
本文将基于逐步I型区间删失样本,运用EM算法得到了Lomax分布形状参数的迭代公式,并通过数值模拟说明迭代公式收敛速度较快,对参数的估计较稳健.
1 形状参数θ的极大似然估计
设总体X服从双参数Lomax分布,其密度函数为
(1)
其分布函数为
(2)
其中λ>0,θ>0,且分别被称为尺度参数和形状参数,假设尺度参数λ已知,将对形状参数θ进行统计推断.
先介绍逐步I型区间删失试验:
为了了解某产品的寿命特征,现投入n个样品进行逐步I型区间删失试验,在预先确定的k个时刻T1,T2,…,Tk时进行观测,且满足0=T0 对于上述试验得到的逐步I型区间删失数据可表示为 {(nj,Rj,Tj),(j=1,2,…,k)} (3) 假设尺度参数λ已知,根据前面的试验数据,用极大似然法来求形状参数θ的极大似然估计.由于 P{X∈[Tj-1,Tj)}=F(Tj)-F(Tj-1)=(1+Tj-1/λ)-θ-(1+Tj/λ)-θ 因此似然函数可以表示为 其中c>0,且与θ无关. 对数似然函数为 (4) 由方程(4)并不能得到形状参数θ的显式解.如果用数值方法求近似解,也不能证明这样的解是唯一的,因此形状参数θ的极大似然估计不容易得到.下面用EM算法来求参数θ的估计. 下面先介绍EM算法. EM算法是一种迭代方法,主要用来求后验分布的极大似然估计,它的每一次迭代由两步组成: E步(求期望 )和 M 步 (极大化).以f(θ|Y)表示根据观测数据Y所得到的θ的后验密度函数,称为观测后验密度,f(θ|Y,Z)表示添加数据Z后得到的关于θ的后验密度函数,称为添加后验分布.f(Z|θ,Y)表示在给定θ和观测数据Y下潜在数据Z的条件密度函数. EM 算法按照如下进行.记θ(i)为第i+ 1次迭代开始时参数θ的估计值,则第i+ 1次迭代的两步为: E步:将f(θ|Y,Z)或lnf(θ|Y,Z)关于Z的条件分布求期望,即 Q(θ|θ(i),Y)=E[lnf(θ|Y,Z)|θ(i),Y] 这样就完成了一次迭代,θ(i)→θ(i+1). 将上述E步和M步进行迭代直至‖θ(i+1)-θ(i)‖ 或‖Q(θ(i+1)|θ(i),Y)-Q(θ(i)|θ(i),Y)‖充分小时停止. 对于前面的逐步I型区间删失试验,记观测结果Y={(nj,Rj,Tj),(j=1,2,…,k)},Zj为落入区间[Tj-1,Tj)的随机变量. 根据条件密度公式,可以得到Zj的条件密度函数为 E步:根据似然函数的定义可以得到 Q(θ|θ(i),Y)≜E[lnf(θ|Y,Z)|θ(i),Y] M步:把Q(θ|θ(i),Y)对θ求导,求出Q(θ|θ(i),Y)的极大值点θ(i+1). (5) 把式(5)左边的θ取为θ(i+1),则得 (6) EM算法的最大优点是估值的稳定性,特别是在删失样本下,它是求参数估计值的一种有效方法.下面的两个引理说明了EM算法的收敛性. 引理1EM算法在每一次迭代后均提高(观测)后验密度函数值,即 f(θ(i+1)|Y)≥f(θ(i)|Y) 引理2(1)如果f(θ|Y)有上界,则L(θ(i)|Y)收敛到某个L·; (2)如果Q(θ|φ)关于θ和φ都连续,则在关于L很一般的条件下,由EM算法得到的估计序列θ(i)的收敛值θ·是L的稳定点. 引理1和引理2的证明见文献[10]. 设总体X服从双参数Lomax分布(2),取定参数值λ=2.5,θ=2,预先确定的7个观测时刻分别为T1=1,T2=2,T3=4,T4=5,T5=6,T6=9,T7=13.随机确定每一观测时刻Ti的截尾数Ri,当取不同的n值时,利用Matlab软件模拟产生了8个逐步I型区间删失样本,列于表1中. 表1 逐步I型区间删失样本 根据表1中的样本,利用Mathematica软件,当取不同的参数初值θ(0)时,进行3次迭代计算,并把第3次的迭代值作为参数θ的最终估计值,计算相对偏差bias(θ(3))/θ=|(θ(3)-θ)/θ|,统计分析结果列于表2中. 表2 EM算法的统计分析结果 从表2中的统计分析结果可以看到,对于服从双参数Lomax分布的逐步I型区间删失样本,利用EM算法的迭代公式(6),经过3次迭代后形状参数θ的估计值趋于稳定,并且相对偏差很小.对于同一样本分别选取不同的参数初值θ(0)=0.5和4.0,经过3次迭代后所得到的θ的估计值θ(3)非常接近,从而说明运用EM算法所得到的形状参数θ的估计值与参数初值的选取没有关系,估计值较为稳健. 参考文献: [1] 葛露娟,周菊玲. Mlinex损失函数下Lomax 分布的几种Bayes 估计[J]. 山东师范大学学报 (自然科学版),2016,31(2):53-56. [2]罗嘉成,陈勇明.逐次定数截尾Lomax分布的贝叶斯分析[J]. 成都信息工程大学学报,2016,31(3):323-326. [3]和阳,王蓉华,徐晓岭. 损伤失效率下 Lomax分布在步进试验下的统计分析[J].兵器装备工程学报,2017,38(7):176-179. [4]王秋平. Q对称熵损失下两参数 Lomax分布形状参数的 Bayes估计[J].佳木斯大学学报 (自然科学版),2015,33(2):314-315. [5]李开灿,刘大飞,林存津. Lomax分布极大似然估计的两点研究[J].数学杂志,2016,36(1):207-213. [6]葛露娟,周菊玲.两两NQD 序列下Lomax分布参数的经验Bayes检验[J].数学的实践与认识,2016,46(17):189-195. [7]黄金超,凌能祥.Lomax分布族形状参数的经验Bayes检验函数的收敛速度[J].数学进展,2016,45(2):280-288. [8]沈新娣,丁帮俊.Pareto分布在逐步II型区间删失下的参数估计[J].应用概率统计,2016,32(2):132-146. [9]任瑞,周秀轻.逐步I型区间删失数据下的参数估计[J].南京师大学报(自然科学版),2011,34(3):7-12. [10]茆诗松,王静龙,濮晓龙.高等数理统计[M].2版 .北京:高等教育出版社,2006: 432-433.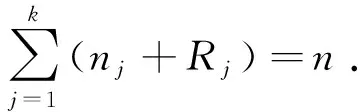
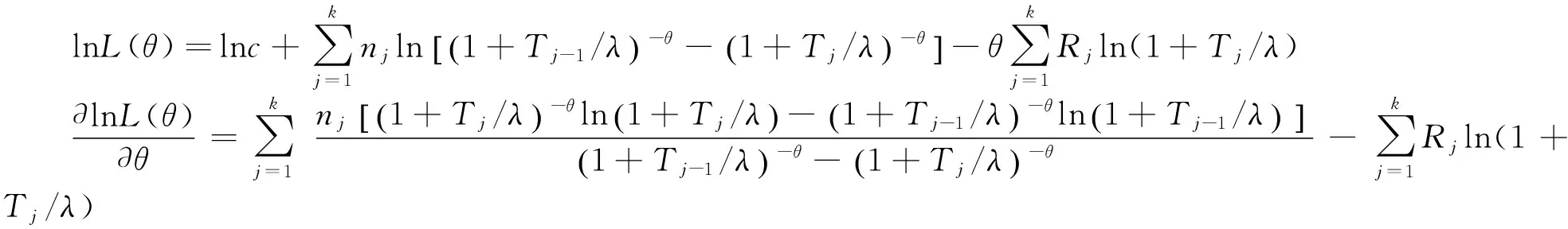
2 用EM算法求形状参数θ的估计
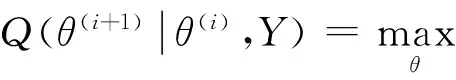
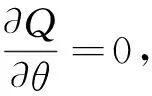

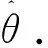
3 数值模拟