带有退化效应和序列相关送出时间的单机排序问题

陈　娟

(重庆师范大学 数学科学学院，重庆 401331)

在传统的排序研究中，一般认为工件的加工时间是固定不变的常数，但是在实际工业生产中，比如钢铁生产、救助资源分配等问题中，工件越靠后加工，加工时间越长，这就是所熟知的退化效应.关于工件退化问题，已经有很多研究，其中Mosheiov[1]考虑了线性模型pj(t)=αjt，并证明了最大完工时间、总完工时间、总加权完工时间、最大延误时间等问题是多项式时间可解的.Bachman等[2]证明了模型pj(t)=aj+αjt极小化最大延误问题是NP难的.Wang等[3]考虑了工件同时带有退化效应和学习效应的单机排序问题，并用启发式算法给出了目标函数为总完工时间问题的解法.

同时，在钢铁工业加工过程中，钢铁由于在加工完成后，温度极高，不能马上运送给客户，需要一些时间冷却，因此工件的等待时间会对工件的总完工时间造成影响.电子元件生产过程中也存在类似的影响.针对这种现象，Koulamas等[4]提出将这种不利影响看作是与工件排序有关的送出时间，为了分析方便，通常假设送出时间与工件的等待时间成正比例，他们就最大完工时间、总完工时间、最大延误时间和延误工件个数问题，分别给出了最优排序规则.Yin等[5]考虑了成比例线性退化的序列相关送出时间的单机排序问题，证明了最大完工时间等问题是多项式可解的，并分析了其他几个目标设计启发式算法的最差性能比.

笔者考虑带有退化效应和序列相关送出时间的单机排序问题，通过把基本加工时间最大的工件放在最后加工得到极小化最大完工时间问题的最优排序，证明SPT序对于极小化总完工时间问题是最优排序，就基本加工时间和权重相反一致情形证得WSPT序对于极小化总加权完工时间是最优排序，就工期和基本加工时间一致情形，证明EDD序对于极小化最大延误问题是最优排序.

1　模型描述与符号介绍

Jj第j个工件，其中j=1,2,...,n.

pj工件Jj的基本加工时间,其中j=1,2,...,n.

b工件Jj的退化率，其中j=1,2,...,n.

a正常数.

t所有工件在t时刻可以加工.

n工件的个数.

dj工件Jj的工期.

wj工件Jj的权.

Cj工件Jj的完工时间.

Lmax工件的最大延误时间.

Cmax工件的最大完工时间.

Cj(S)排序S中的工件Jj的完工时间.

C[j](S)排序S中第j个位置上的工件的完工时间.

q[j]排在第j个位置工件的序列相关送出时间.

假设有n个独立的工件，用集合表示为J={J1,J2,J3,…,Jn},放在一台机器上加工，n个工件无优先加工权，并且在0时刻都可加工，所有工件在加工过程中不允许中断，一台机器也不能同时加工两个或两个以上的工件，工件Jj的实际加工时间表示为：

(1)

为了叙述方便，把方程(1)记为LD.如前所述的送出时间，通常假设送出时间与工件的等待时间成正比例，排在第j个位置工件的序列相关送出时间可表示为：

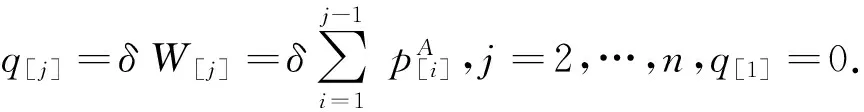
j=2,3,…,n.

第一个工件的完工时间

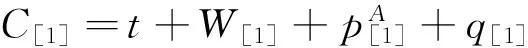
第j个位置上工件的完工时间：

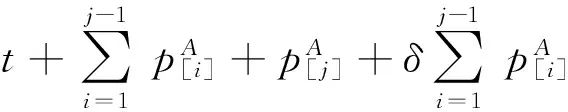
用∑Cj、∑wjCj、Lmax分别表示总完工时间、加权总完工时间、最大延误时间，本文研究的问题用三参数表示法[6]表示如下：

1|LD,qpsd|Cmax

1|LD,qpsd|∑Cj

1|LD,qpsd|∑wjCj

1|LD,qpsd|Lmax

2　主要结论

定理1对于问题1|LD,qpsd|Cmax，只要满足p[n]=max{p1,p2,…,pn}的排序即为最优排序.

证因为

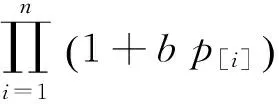
推论1对于问题1|LD,qpsd|Cmax，按照上述算法得到的最优排序，其计算复杂性是O(n).

证因为只需要找出n个工件中基本加工时间最大的工件，所以其计算复杂度为O(n).

上面证明了任何一种p[n]=max{p1,p2,…,pn}的排序对于问题1|LD,qpsd|Cmax都是最优的.接下来研究总完工时间问题.

定理2对于问题1|LD,qpsd|∑Cj，将所有工件按照基本加工时间非减(即：SPT原则)顺序排列可得到最优排序.

证假设存在一个最优排序S=(π1,Ji,Jj,π2)，其中工件Ji和Jj分别在两个相邻的位置，π1和π2是部分排序并且可能为空，假定π1中有r-1个工件，因此工件Jj和Ji分别在第r个和r+1个位置上，并且假定pipj，而通过交换工件Jj和Ji的位置得到另一个排序S'=(π1,Jj,Ji,π2)，为了证明排序S的总完工时间不大于排序S'，实际只需证明Ci(S)+Cj(S)Ci(S')+Cj(S')和Cj(S)Ci(S')，而

Ci(S)=

Cj(S')=

因为pipj，容易看出Cj(S)Ci(S')，Ci(S)Cj(S')，因此得Ci(S)+Cj(S)Ci(S')+Cj(S')，定理得证.

推论2对于问题1|LD,qpsd|∑Cj，按照SPT规则得到的最优排序，其计算复杂度为O(nlogn).

证因为是按照SPT规则排列，因此计算复杂度为O(nlogn)[7].

定理2用SPT规则解决极小化总完工时间问题，定理3则通过添加一个限制条件，解决了总加权完工时间的问题.

定理3对于问题1|LD,qpsd|∑wjCj，当任意工件Ji和Jj满足pipj并且wi≥wj时，则工件按照(即WSPT规则)能得到最优排序.

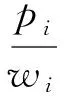
wjCj(S')+wiCi(S')-wiCi(S)-wjCj(S)

≥wjCi(S)+wiCj(S)-wiCi(S)-wjCj(S)

=(wi-wj)(Cj(S)-Ci(S)),

因为wi≥wj，(wi-wj)(Cj(S)-Ci(S))≥0，定理得证.

通过增加一个限制条件，用WSPT规则解决了问题1|LD,qpsd|∑wjCj. 接下来就是关于极小化最大延误的问题.

定理4对于问题1|LD,qpsd|Lmax，当任意工件Ji和Jj满足当pipj，didj时，则工件按照dj非减的顺序(即EDD原则)可得到最优排序.

证基于定理2的证明，进一步假设排序S满足didj,并且

Cj(S)Ci(S') ，Ci(S)Cj(S')和Cl(S)=Cl(S')

其中l≠i和j, 只需证max{Li(S),Lj(S)}max{Li(S'),Lj(S')}. 由Lj的定义可得：

Li(S)=Ci(S)-di

Lj(S)=Cj(S)-dj

Li(S')=Ci(S')-di

Lj(S')=Cj(S')-dj

因为didj，并且Ci(S)Cj(S)Ci(S')，所以Lj(S)Li(S')，Li(S)Li(S'),从而得max{Li(S),Lj(S)}max{Li(S'),Lj(S')}，定理得证.

3　结语

本文考虑带有退化效应和序列相关送出时间的单机排序问题，通过把基本加工时间最大的工件放在最后加工得到了极小化最大完工时间问题的最优排序，并给出了其计算复杂度O(n)，证明了SPT序对于极小化总完工时间问题是最优排序，给出了计算复杂度O(nlogn)，就基本加工时间和权重相反一致情形证得WSPT序对于极小化总加权完工时间是最优排序，就工期和基本加工时间一致情形，证明了EDD序对于极小化最大延误问题是最优排序.今后主要是考虑通过找到最优交货期窗口的位置，交货期窗口的大小和一个最优排序，使成本函数

的取值最小.

参考文献：

[1]G Mosheiov.Scheduling jobs under simple linear deterioration[J]. Computers & Operations Research, 1994,21: 653-659.

[2] A Bachman, A Janiak, M Y Kovalyov. Minimizing the total weighted completion time of deteriorating jobs[J]. Information Processing Letters, 2002,81: 81-84.

[3] Wang J B,Wang M Z,Ji P. Single machine total completion time minimizationsched- uling with a time-dependent learning effect and deteriorating jobs[J]. International Journal of Systems Science, 2012, 43:861-868.

[4]Koulamas C,Kyparisis G J. Single-machine scheduling with past-sequence-dependent delivery times[J]. International Journal of Prodution Economics, 2010, 126:264-266.

[5] Yin Y Q, Cheng T C E, Xu J Y, et al. Single-machine scheduling with past-sequence-dependent delivery times and a linear deterioration[J]. Journal of Industral and Management Optimizati- on, 2013, 9(2):323-339.

[6] Graham R L, Lawler E L, Lenstra J K,et al. Optimization andappr-oximation in deterministic sequencing and scheduling: A survey[J]. Annals of Discrete Math- ematics, 1979, 5:287-326.

[7]Pinedo M L. Scheduling : Theory, Algorithms and Systems[M]. NJ: Prentice-Hall, Englewood Cliffs, 1995:28-31.