不等式的推广及其应用

罗　群

（肇庆学院 数学与统计学院，广东 肇庆　526061）

0　引言

本文讨论式（1）的推广形式，所讨论的问题有

证明本文结论的主要依据是下面的引理1.

引理1[1]126设函数 f(x)在区间I上可导，若 f′(x)＞0(f′(x)＜0),则 f(x)在区间I上严格递增（严格递减）.

1　主要结论

结论1当α≤3时，不等式成立.

由引理1，f′(x)在(0,π/2)内严格单调增，而 f′(x)在x=0右连续，所以

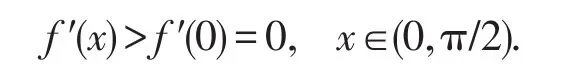
因此，当0＜α≤3时，在(0,π/2)内总成立 f′(x)＞0.又由引理1，f(x)在(0,π/2)内严格增，且 f(x)在x=0右连续，于是

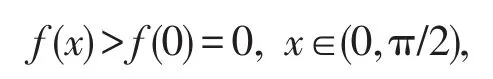
即不等式（2）成立.

综上，当α≤3时，不等式（2）成立.

结论2当α＞3时，不等式

由引理 1，g(x)在 (0,π/2)内严格增，而 g(xα)=0,所以当 x∈(0,xα)时，g(x)＜g(xα)=0,由于因此 f″(x)＜0.由引理1，f′(x)在 x∈(0,xα)内严格减，而 f′(0)=0,从而当 x∈(0,xα)时，有 f′(x)＜f′(0)=0,故 f(x)在(0,xα)内严格减，从而

于是所证结论成立.

结论3当α＞3时，存在x0∈(0,π/2),使得当x∈(x0,π/2)时，不等式

成立.

取大的生荸荠20枚，去节鲜莲藕150克，大的梨子2枚，捣烂绞汁生饮。适用于肺癌咯血、咳血或放射治疗后咽焦干咳者。

证函数 f(x),g(x)与结论2证明中相同.由结论2的证明过程可知，由于g(x)在(0,π/2)内严格增且g(xα)=0,因此当x∈(xα,π/2)时，g(x)＞0,从而 f″(x)＞0,于是 f′(x)在(xα,π/2)内严格增.由 f(x)的定义及 f′(x)的表达式（3），有

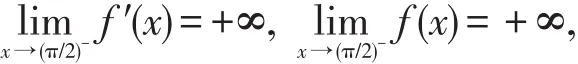
因此，存在x0∈(xα,π/2)⊂(0,π/2),使得 f(x0)＞0且 f(x)在(x0,π/2)严格增，故不等式（5）成立.

2　应用

例1证明不等式

证式（6）等价于tan x sin x＞x2,即由结论1显然成立.

例2[2]证明

证1）当x=±π/2时，所证不等式为(2/π)3＞0,显然成立；

2）当x∈(0,π/2)时，由结论1，所证不等式成立；

3）当x∈(-π/2,0)时，由于不等式两端均为偶函数，由2）可知结论也成立.

例3证明：1）当0≤α≤2时，不等式

成立.

2）当α＜0时，不等式

成立.

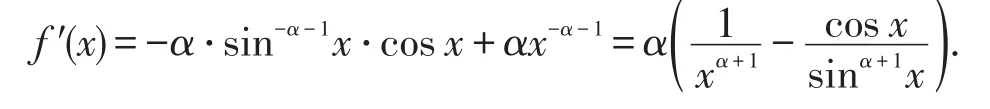
1）当0≤α≤2时，有α+1≤3,由结论1，f′(x)＞0,从而 f在(0,π/2)严格增；又 f在x=π/2处左连续，因此当从而不等式（7）成立.

2）当α＜0时，有α+1＜1,由结论1，f′(x)＜0,从而 f在(0,π/2)严格减；又 f在x=π/2处左连续，因此当从而不等式（8）成立.

注特别地，当α=2时，有如下不等式[3]成立：

例4证明不等式

参考文献：

[1]华东师范大学数学系.数学分析：上册[M].4版.北京：高等教育出版社，2010.

[2]裴礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社，2002：206.

[3]许康,陈强,陈挚,等.前苏联大学生数学奥林匹克竞赛题解：上编[M].哈尔滨：哈尔滨工业大学出版社，2012：45.