基于分散式压缩感知的低能耗信号重构模型

李　博，李云鹤，李广才

（肇庆学院 电子信息与机电工程学院，广东 肇庆　526061）

1　概述

由采样定理知，只有当采样率大于2个信号带宽时，才能知道相似信号可用高质量的方法进行恢复.这些年随着信息量的增加，信息传送的带宽得到了提高，对信息获取时的采样和处理速度要求也变得越来越高.Donoho、Candes和其他专家学者[1-3]在其研究中详细说明了压缩传感理论，其采样标准要比Nyquist低很多，用这种方法重建原始信号非常可靠.信号复原是重要的，这一点无可争议，而其难点在于将理论付诸实践.贪心算法、凸优化算法[4-5]和组合优化算法[6-7]都是用于理论的通用方法.这些算法牺牲了复原的精确性和复杂性，使用迭代来持续更新支撑集，最终接近原始信号，其中包含了很多门类，主要包含倒溯法（一种基于正交匹配追踪算法OMP的算法）[8-9].倒溯法重构的精确性相对较高，子空间追踪算法在此门类中为代表性方法，其在各方面均有许多优势：较低的复杂度和较高的精确度；但是，与规则OMP即ROMP算法[10]相比，信号已知稀疏度是精确重构原始信号的基本条件.其1次迭代会被投影2次，投影的复杂性随着稀疏度的提高而急剧上升，从而对重构信号的质量造成严重影响并将其变小.

为弥补以上缺陷，本文设计了一个应用范围较大并且高效的信号重构法.通过快速稀疏度评估的方法处理稀疏度未知的信号；同时，在重构过程中，避免了迭代时产生的观测向量的投影运行，进一步减少运行的复杂性.在深入总结现存指数后，提供了更全面和科学的评估分析指数，以此来评估带缺陷的当前重构算法的性能.

2　本文算法

考虑到目前的方法只能重构稀疏度已知的信号，笔者在文中设计的重构法中使用一个快速评估方法，它可以有效提高疏密度评估的效率，在很大程度上缩短疏密度预估值与实际值的差距.另外，文中的算法储存了候选集观测向量的投影过程，这个候选集是传统追踪算法的一部分.通过这种方法，其集合被全部储存起来；避免了支撑集上的投影步骤，让这个步骤最终简单易懂.

2.1　疏密度的评估

首先在这里详细说明评估方法.在将被重构的信号中，受限等距性质是重构的基础.该性质表现如下：如果向量x满足‖x‖0≤K,那就有一个矩阵A满足如下条件：

A满足(K,d)参数条件下的受限等距性.在方程中，‖x‖2是xl2的范数，得出不等式(1)的最小值dK,0＜dK＜1.

上述性质导出了下列法则1.

法则1假设信号稀疏度为k,A满足(K,d)参数条件下的受限等距性.若k=K,则

公式（2）中，|(A,y)|表示向量y和第i个A之间的向量绝对值，G0是k的最大值，AG0是由A和G0组成的子矩阵.

例1假设信号稀疏度是k,A满足基于(K,δ)系数的受限等距性质，当k3K,则

根据例2的逆否命题，可得推论1.

推论1假设A符合(K,δK)的特性.当预估稀疏度

法则1可以根据推论1和例1证明.

使ui=在递减的途径中安排ui,形成一个新的数列.然而这样方程（3）可以按照如下描述：

使用符合公式（4）的最大数k作为稀疏度K的下限，记为Kmin;符合公式（4）的最大值表示下舍入.

与之前的方法作比较，仅总结了U′中元素的平方数，将公式（4）中第1次和最后1次的元素数量记为Kmin和Kmax,这样就避免了检验，因此花费的时间减少了很多.在相关专家的研究结果中[11-12]，当稀疏度处于上限或下限时，应该停止运行，因为这会造成稀疏度预估值的误差较大.比如，当实验性稀疏度接近下限时，实际值就接近上限，将代入就可以终止上述情况，使预测结果更精确.

2.2　算法的迭代过程

一般在迭代算法中，迭代过程分别在候选集和支撑集上，必须要介入1次关联最大化（correlation maximum，简称CM），还必须经过1次投影运行.为了简化描述，使用proj(Cn)和proj(Sn)来表示第n个迭代中，候选集Cn和支撑集Sn各自的观测向量y的投影过程[9].相关专家和学者表示迭代过程的复杂性主要在于CM，但并未注意重构方法上第2个投影的严重干涉.针对这个，本文专门分析了单个迭代过程的复杂性.当y和A分别为M×1和M×N维度矩阵时，每个CM过程必须要经过M×N次的相乘，O(MN)表示其复杂性.通过MGS（modified gram schmidt）方法[13-14]得出proj(Sn),复杂性为O(MN2).假设在第n个迭代候选集中有Vn个元素，则在此背景下K≤Vn≤2K,O(MV2n)为计算得出proj(Cn)的复杂性.整个迭代的计算复杂性为O(MN+Mv2n+MK2).当K较小时，可以将其视为O(MN);当K持续增加，上面第2个投影的复杂性将急剧上升.这个时候，它对重构法复杂性的影响要比CM大很多.

本文设计的重构方法理论如图1所示：在实现重构算法集合保持基本不变的情况下，减少迭代中的投影次数，使算法的复杂性降低.首先使用预估算法决定K后，执行迭代重构.在第n个迭代中，每个A列的最后1个迭代的关联余量rn-1,加上关联系数绝对值的最大数K和最后迭代的sn-1,根据这个条件形成Cn.然后把y投影到Cn,使用投影绝对值的最大系数k作为这一轮的Sn,使用Sn的投影值作为此次迭代中重构信号Zn的非零部分ZSn;可以决定当前迭代余量rn=y-ASnZSn,当它满足|rn|＞|rn-1|时，迭代过程终止；若其不满足这个条件，则继续下一个迭代.当Sn是指数列时，ASn是A中产生的子矩阵.图1展示了这个特殊演变的步骤.

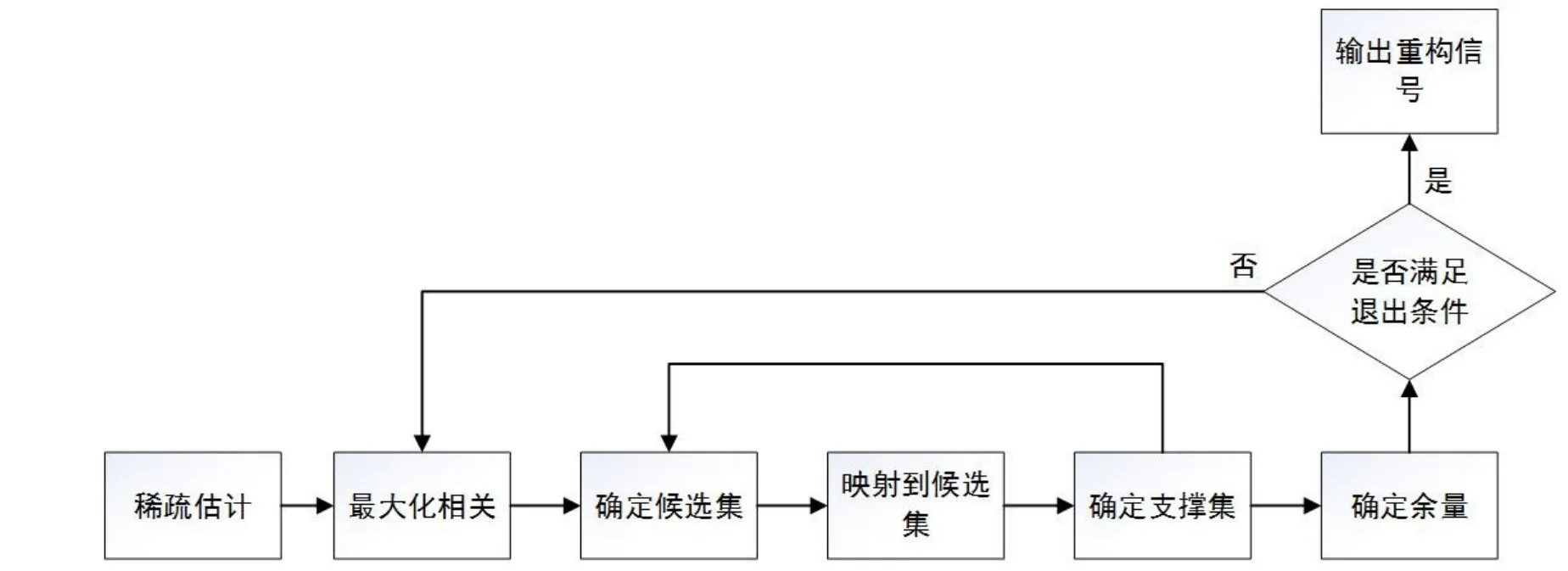
图1　设计算法的基本步骤

3　算法的重构性能指数

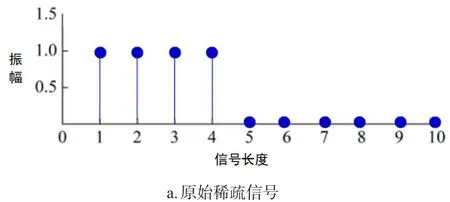
稀疏信号重构过程中，会造成重构幅度和位置的2个误差，如图2所示.图2a是原始稀疏信号，其长度和稀疏度分别为10和4；图2b和图2c为当幅度和位置误差分别发生时的重构稀疏信号.将稀疏信号幅度中非零部分的重构可能性定义为I，将II定义成整个稀疏信号的重构可能性.当│重构信号-原始信号│不大于10-8时，那么构建成功.重构信号如图2b和图2c所示，相应的重构可能性I和II分别为0.75和0.9；0.75和0.8.主要方法是使用I作为评估算法重构性能的指数，但是在研究中发现：当I相同时，重构误差不同，II也会不同.无法说明这2个重构误差，所以无法仅通过I来判断整个系数信号的重构可能性.

在重构过程中，最好的结果是重构了整个系数信号，而不仅仅只重构非零部分.为解决这个问题，将II用作评估指数来判断文中方法的重构性能，下面进行模拟分析.

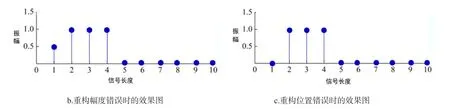
图2　重构信号的2个误差

4　稀疏度的评估

首先，通过仿真判断本文推荐的稀疏度预估法的精确度（下文称为OASP）.实验中，采样次数M和信号长度分别为128和256；所观察的矩阵是一个M×N维度的高斯随机矩阵；其结果为1 000次模拟输出的平均数.不同K值下稀疏度预估的对比情况如图3所示，图3对比了K=36时各个δk值上的估值.通过分析，得知当δk=0.15时，估值和实际值的差距为最小，而且比较稳定.

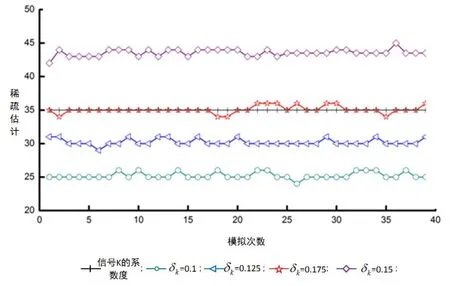
图3　不同K值下稀疏度预估的对比

2种方法模拟次数的对比如表1所示.对比2种不同方法的模拟次数，也就是1 000次Monte Carlo实验的总和.实验中，N=512,M=256,当结束条件相同时，测试2个不同信号重构算法的次数.通过对比OASP和SP，从表1中可以发现，在任何稀疏度之下，前一个算法的时间要比后者短，而且随着K的持续增加，前者减少的时间变得愈加明显.

对比获得结束条件相同的2个算法的迭代次数，情况如图4所示.实验中，N=256，M=138，结果为500次Monte Carlo实验输出的平均值.由图4可以发现：当K较小时，2个获得结束条件相同的算法的迭代次数几乎相同，接近log(K).当K持续增加时，前一个算法的迭代次数的幅度也逐渐增加时，而后一个算法正好相反，因此，前者节约的时间将随着K的逐渐增加而增加.

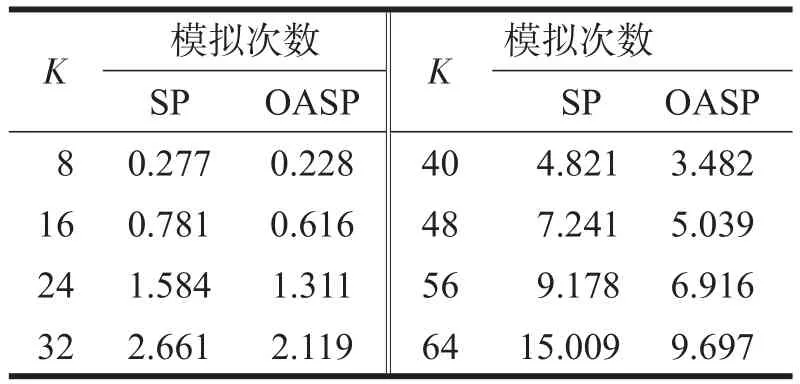
表1　2种方法的模拟次数的对比

分析不同算法中不同K值下的II的对比情况，如图 5所示.实验中，N=256,M=128.当|重构信号-原始信号|≤10-12时，重构成功，其结果是1 000次Monte Carlo实验的输出平均值.同时，分析了许多其他方法，比如SAMP（稀疏度适应性配对追求法）[15-16].在图5中发现ROMP，OMP和SAMP在K=56的时候会逐渐丧失其性能；此时，SP算法具有良好的重构能力，而在K=56时开始丧失；注意到K=60时OASP丧失了其效果.根据上述对比，发现本文详细描述的算法具备最明显的优势，在稀疏信号的重构完成中具有最高效用.尽管本文展示的算法拥有明显优势，随着K进一步增加，II的减少幅度很大，但是SAMP的减少幅度相对较低.

图4　迭代次数

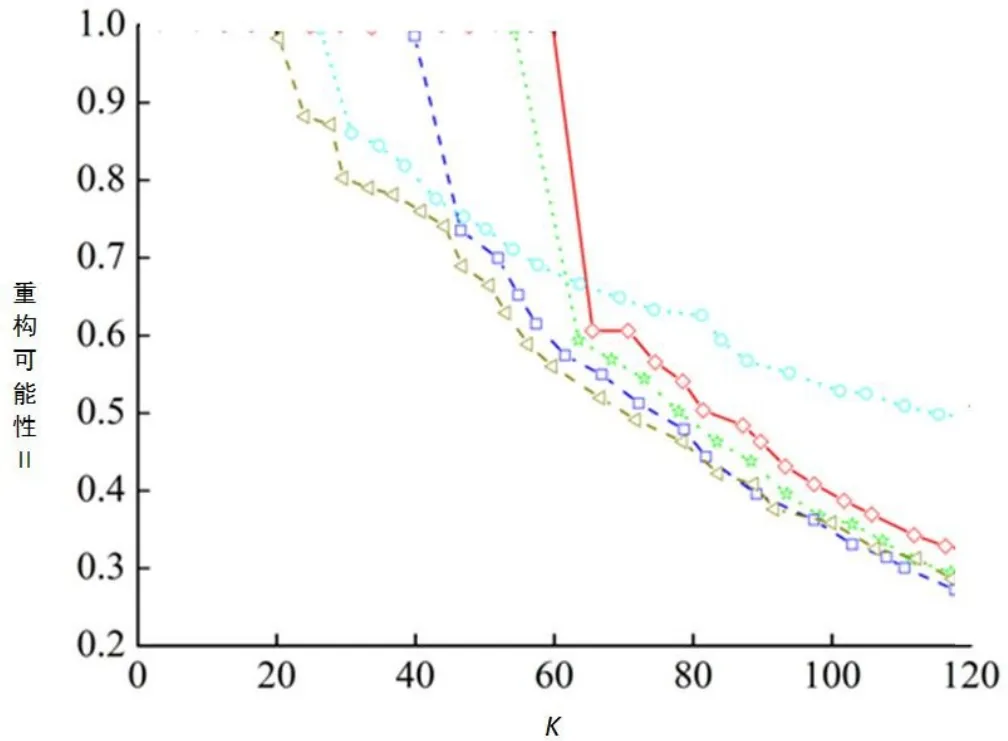
图5　不同算法的重构可能性II的对比

5　总结

为有效解决未知稀疏度压缩信号的快速重构，笔者在本文中提出了一个应用范围宽阔、效果卓越的信号重构方法.以等距性质为基础，获得压缩信号的上、下边界，而最接近其中间值的整数为信号稀疏度的预估值；减少迭代中投影在支撑集上观测向量的次数，从而降低此方法的算法复杂性；推出了一个可以反映整个信号重构可能性的预估系统，该系统证实并分析了该方法的效果.实验显示该方法有效地实现了未知稀疏度信号的快速重建，而且其重构的成功可能性要比当前的倒溯法要高.

参考文献：

[1]LV Z.Managing big city information based on WebVRGIS[J].IEEEAccess,2016(4)：407-415.

[2]HU Jinyu,GAO Zhiwei.Modules identification in gene positive networks of hepatocellular carcinoma using Pearson agglomerative method and Pearson cohesion coupling modularity[J].Journal ofApplied Mathematics,2012(3)：1-16.

[3]WANG K,ZHOU X,LI T.Optimizing load balancing and data-locality with data-aware scheduling[C].Big Data：IEEE 2014 IEEE International Conference,2014：119-128.

[4]GENG Yishuang,CHEN Jin,FU Ruijun,et al.Enlighten wearable physiological monitoring systems：On-body rf characteristics based human motion classification using a support vector machine[J].IEEE transactions on mobile computing,2015,1(1)：1-15.

[5]LV Z,HALAWANI A,FENG S.Multimodal hand and foot gesture interaction for handheld devices[J].ACM Transactions on Multimedia Computing,2014,11(1s)：10.

[6]ZHANG L,HE B,SUN J.Double image multi-encryption algorithm based on fractional chaotic time series[J].Journal of Com-putational and Theoretical Nanoscience,2015,12：1-7.

[7]SU T,LV Z,GAO S.3d seabed：3d modeling and visualization platform for the seabed[C].Multimedia and Expo Workshops(ICMEW)：2014 IEEE International Conference,2014：1-6.

[8]LIANG Ying,WANG Peigang.Influence of prudential value on the subjective well-being of chinese urban-rural residents[J].Social Indicators Research,2014,118(3)：1 249-1 267.

[9]LIANG Ying,LI Shuqin.Landless female peasants living in resettlement residential areas in China have poorer quality of life than males：results from a household study in the Yangtze River Delta region[J].Health and Quality of Life Outcomes,2014(12)：71,1-17.

[10]LV Z,TEK A,DA F.Game on,science-how video game technology may help biologists tackle visualization challenges[J].Plos One,2013,8(3)：e57 990.

[11]SU T,WANG W,LV Z.Rapid Delaunay triangulation for randomly distributed point cloud data using adaptive Hilbert curve[J].Computers&Graphics,2016,54：65-74.

[12]HU Jinyu,GAO Zhiwei,PAN Weisen.Multiangle social network recommendation algorithms and similarity network evaluation[J].Journal ofApplied Mathematics,2013：3 600-3 611.

[13]LIU Guanxiong,GENG Yishuang,KAVEH P,Effects of calibration RFID tags on performance of inertial navigation in indoor environment[C].Networking and Communications(ICNC)：2015 International Conference on Computing,2015.

[14]HE Jie,GENG Yishuang,WAN Yadong,et al.A cyber physical test-bed for virtualization of RF access environment for body sensor network[J].IEEE Sensor Journal,2013,13(10)：3 826-3 836.

[15]ZHOU Shuang,MI Liang,CHEN Hao,et al.Building detection in Digital surface model[C].2013 IEEE International Conference on Imaging Systems and Techniques(IST),2012.

[16]HE Jie,GENG Yishuang,KAVEH P.Toward accurate human tracking：Modeling time-of-arrival for wireless wearable sensors in multipath environment[J].IEEE Sensor Journal,2014,14(11)：3 996-4 006.