基于混沌冗余和阈值控制的联合算术码双向编译码快速算法

鄢懿，凃国防，张灿，高绍帅，陈德元



基于混沌冗余和阈值控制的联合算术码双向编译码快速算法

鄢懿，凃国防，张灿，高绍帅，陈德元

（中国科学院大学电子电气与通信工程学院，北京 101408）

JPEG2000是一种具有高效压缩性能的图像压缩标准，但抗差错能力和安全性不能满足实际应用要求。基于此，提出一种基于混沌冗余和阈值控制的联合算术码双向编译码快速算法，在编码端保留多个冗余符号，用混沌系统控制冗余符号的比例增强算术码编码的安全性；在译码端采用阈值控制和双向译码相结合，实现基于最大后验概率的联合快速译码。仿真结果表明，所提算法相对现有算法改善了重建图像质量，同时降低译码复杂度，具有良好的抗差错性和安全性。

加密抗差错算术码；混沌映射；阈值控制；双向译码；JPEG2000

1 引言

JPEG2000作为新一代静态图像压缩标准[1]，广泛应用于雷达遥感、多媒体、数据库、无线通信等领域。相比于JPEG标准，JPEG2000具有高压缩性、渐进式传输、感兴趣区域编码以及码流的随机访问等优点。但由于使用了算术码[2]，JPEG2000对误码非常敏感，在有噪信道中出现的单个误码会使整个码块被丢弃。

一种解决误码扩散的方法是采用抗差错算术码。Boyd等[3]提出了一种在编码过程中添加单冗余符号的方法使算术码具有检错能力。Grangetto等[4]在算术码的译码过程中采用序列估计，通过输入序列的软信息，并利用单冗余符号检错，实现最大后验概率译码。Bi等[5]将算术码的译码过程表示为有限状态机模型，采用Viterbi软译码算法进行译码。Zezza等[6]将单冗余符号算术码应用到JPEG2000中。这些抗差错算术码均在编码过程中仅增加单冗余符号，译码端采用软判决译码，译码复杂度较高。

另一种解决错误扩散的方法是对数据块中的编码数据进行错误检测和掩盖。Gao等[7]提出部分反向比特流方法，将码流分为2个部分，并将后半部分码流进行反转，使同步码在2个方向同步。Gao等[8]提出双向可译变长数据块方法，对编码后得到的数据进行平移、反转和异或，使译码器能实现双向译码。但这2种方法都是针对视频数据进行处理，并不能直接用于JPEG2000的码流结构中。

由于数据的可访问性，传输数据容易遭到窃听，保障信息的安全性显得尤为重要。由于混沌理论具有良好的特性，近年来，混沌加密受到了研究者的广泛重视。Mi等[9]将混沌与算术编码结合，通过Logistic映射和明文得到的密码流，控制算术编码过程中的区间位置，从而对明文进行加密。Wang等[10]将混沌应用到DNA编码中，先用PWLCM生成一个密码图像，将明文图像和密码图像按DNA编码规则编码，用Logistic映射选择当前行/列的编码规则。

为了提高JPEG2000的抗差错性和安全性，本文提出一种基于混沌冗余和阈值控制的联合算术码双向编译码快速算法。该算法在算术码编码模型中保留多个冗余符号，用混沌系统控制冗余符号的比例，增强算术码编码的安全性；在译码端通过计算相应的阈值，采用阈值控制的软硬判决相结合方法进行快速译码降低译码复杂度；同时，针对算术码错误扩散的问题，采用双向译码的方法，提升算术码的纠错能力。仿真结果表明，所提算法在实现高效压缩的同时，具有良好的抗差错性和安全性。

2 基于加密抗差错和阈值控制的联合算术码双向编译码

本文提出的基于混沌冗余和阈值控制的联合算术码双向编译码快速算法框架如图1所示。原始图像预处理后进行离散小波变换，对产生的小波系数量化，按照二进制位分层的方法，从最高有效位平面到最低有效位平面依次进行算术编码，然后根据码率控制后组装成最终的压缩码流；压缩码流经有噪信道后拆分得到各个码块数据，进行算术译码和位平面译码，再反量化、离散小波反变换和后处理，得到重建图像。所提算法的主要工作在图1中虚线部分，包括以下3点。

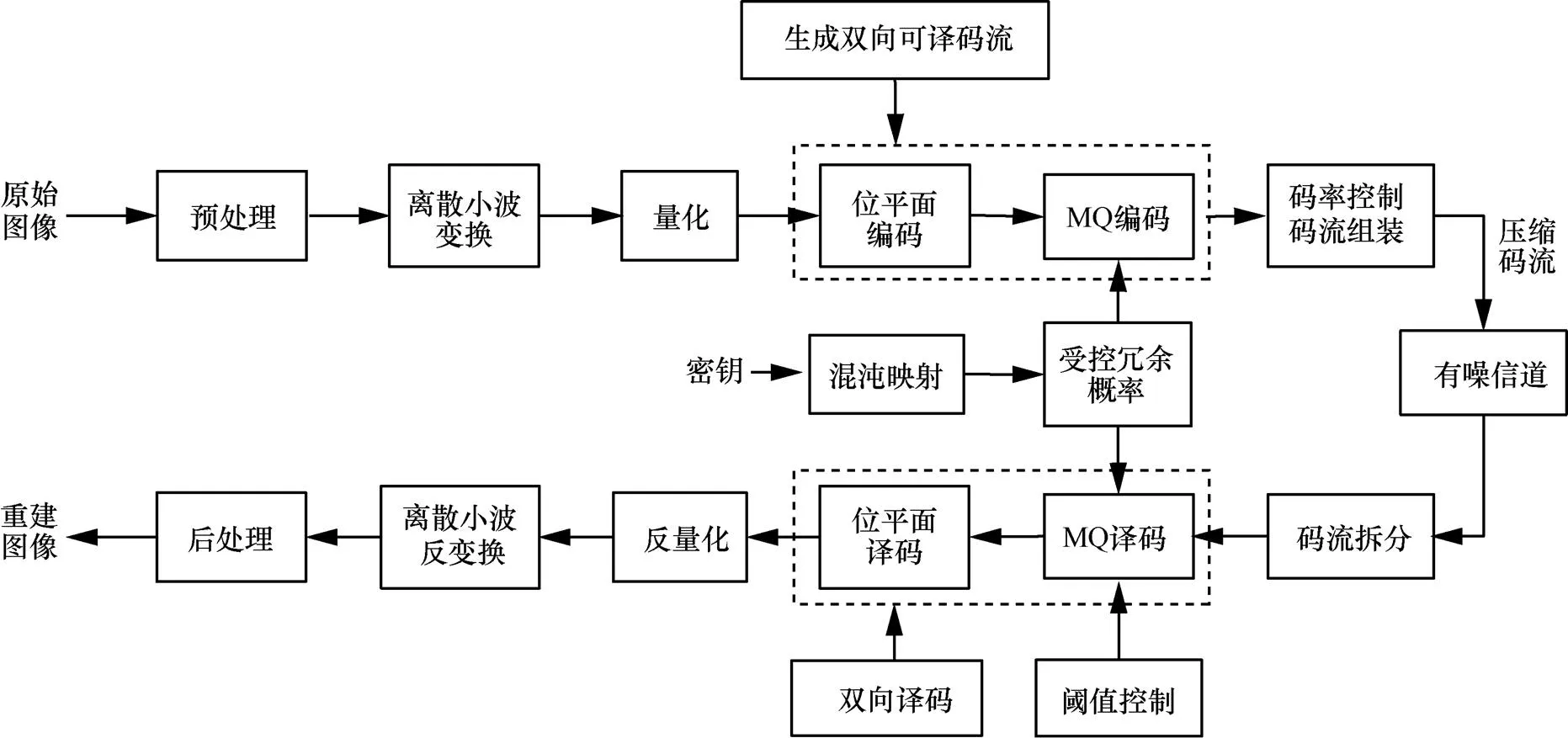
图1 基于混沌冗余和阈值控制的联合算术码双向编译码快速算法框架

1) 加密抗差错算术码：MQ编码器中保留多个冗余符号，密钥通过混沌映射生成混沌序列，控制MQ编码器中冗余符号的比例，增强算术码的安全性。

2) 阈值控制的算术码译码：根据当前的信道条件和传输要求，通过计算相应的阈值，MQ译码器采用阈值控制的软硬判决相结合方法进行快速译码，实现译码性能和复杂度的折中。

3) 双向编译码方法：位平面编码中，对位平面的每个条带独立编码，条带编码后得到的数据块进行平移、反转和异或，生成双向可译码流；译码时，先进行正向译码，当正向译码出现错误时，对码流进行反向译码，纠正译码错误，减少错误扩散。

2.1 加密抗差错算术码

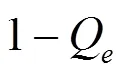
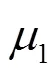
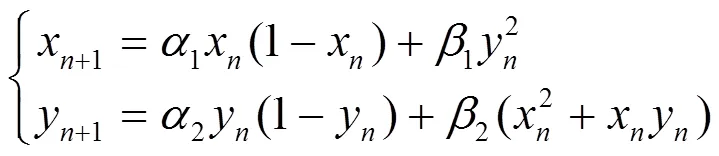
1) 初始化混沌映射的初值和参数。

2.2 阈值控制的算术码译码

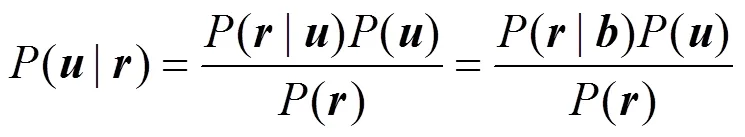
将式(2)取对数得到路径的度量，即

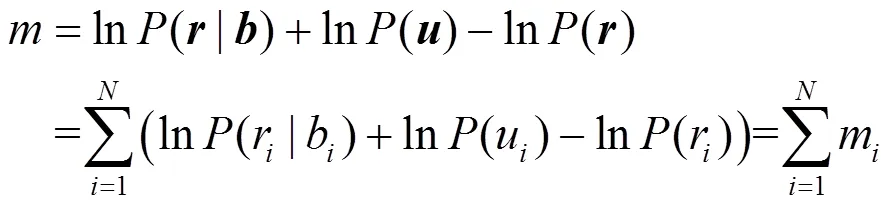
对于AWGN信道软判决输出，经推导，有

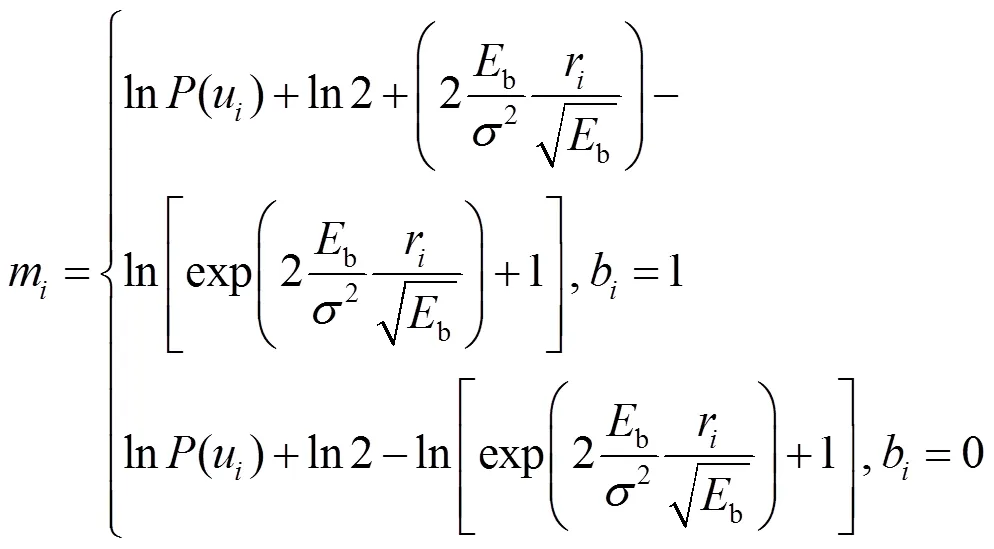
MQ译码器是以字节为单位读取码字序列进行译码的，因此，在按照式(3)和式(4)进行MAP序列估计时，以字节为单位，每个状态可以伸展出256个分支。由于伸展的分支数较多，只能采用深度优先算法，本文选择堆栈算法作为搜索的算法[14]。在算法的每一步，只延伸最顶端路径的后续分支及相应的分支度量，然后，将这些新的分支路径与堆栈中的其他路径按度量大小进行排序，度量最大的路径放在堆栈最顶端，并去除度量较小的路径。如此不断重复，以最大度量为基准延伸路径。

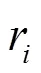
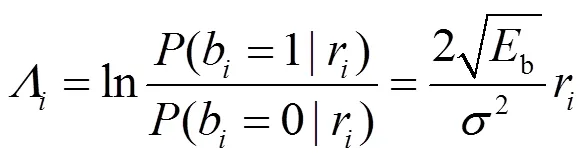
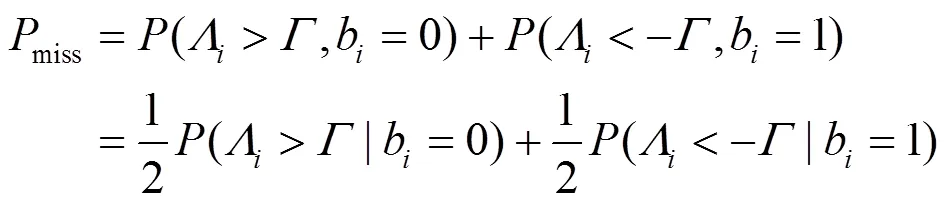
将式(5)代入式(6)，可得

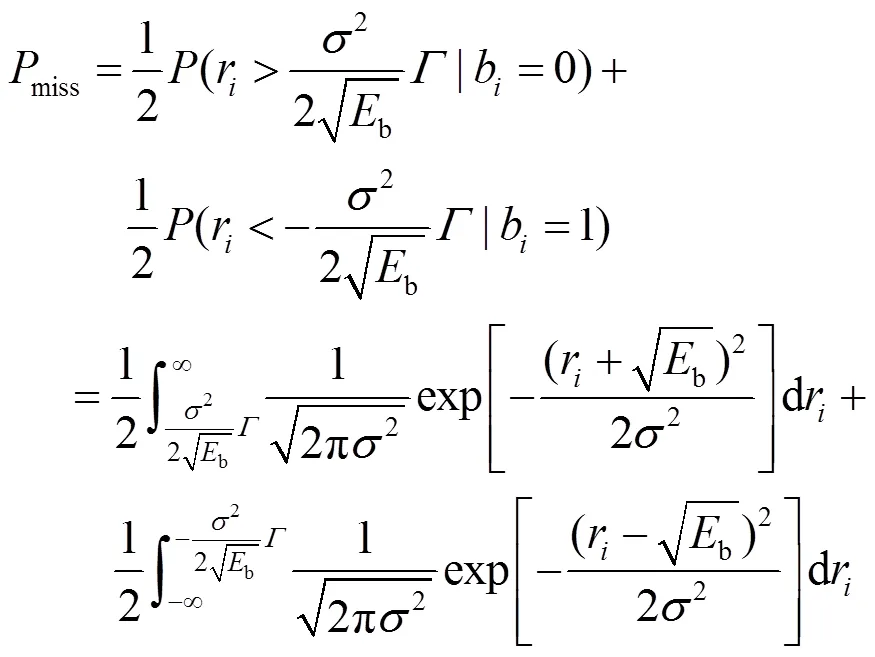
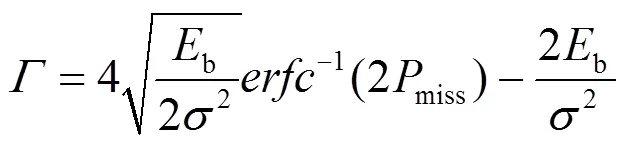
2.3 基于JPEG2000标准的双向编译码方法

理论上来说，与其他译码算法一样，本文提出的阈值控制的算术码译码算法也可能译码失败。特别是当信道中出现突发差错时，由于累积度量变化较大，将正确路径删除的概率就很大。而对于JPEG2000，译出码块中若发生错误，则整个码块将被丢弃，影响图像质量。

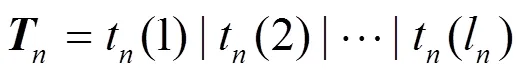
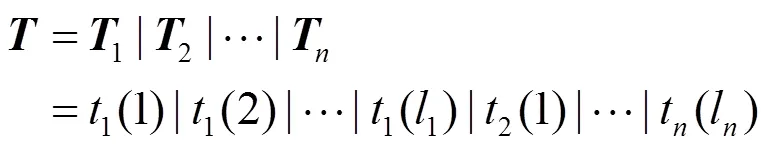
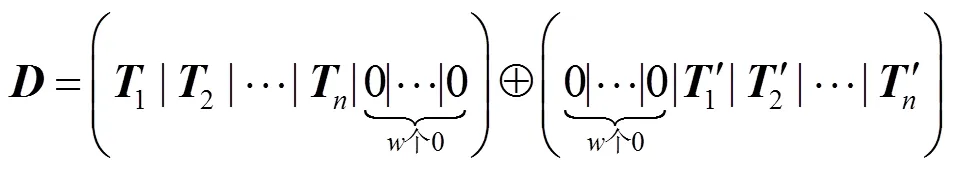
其中，为位平面中条带的最大码字长度。

通过双向编译码方法，压缩码流在译码端不但可以进行正向译码，当正向译码出现错误时，也可进行反向译码，实现码流的双向译码。

1) 正向译码

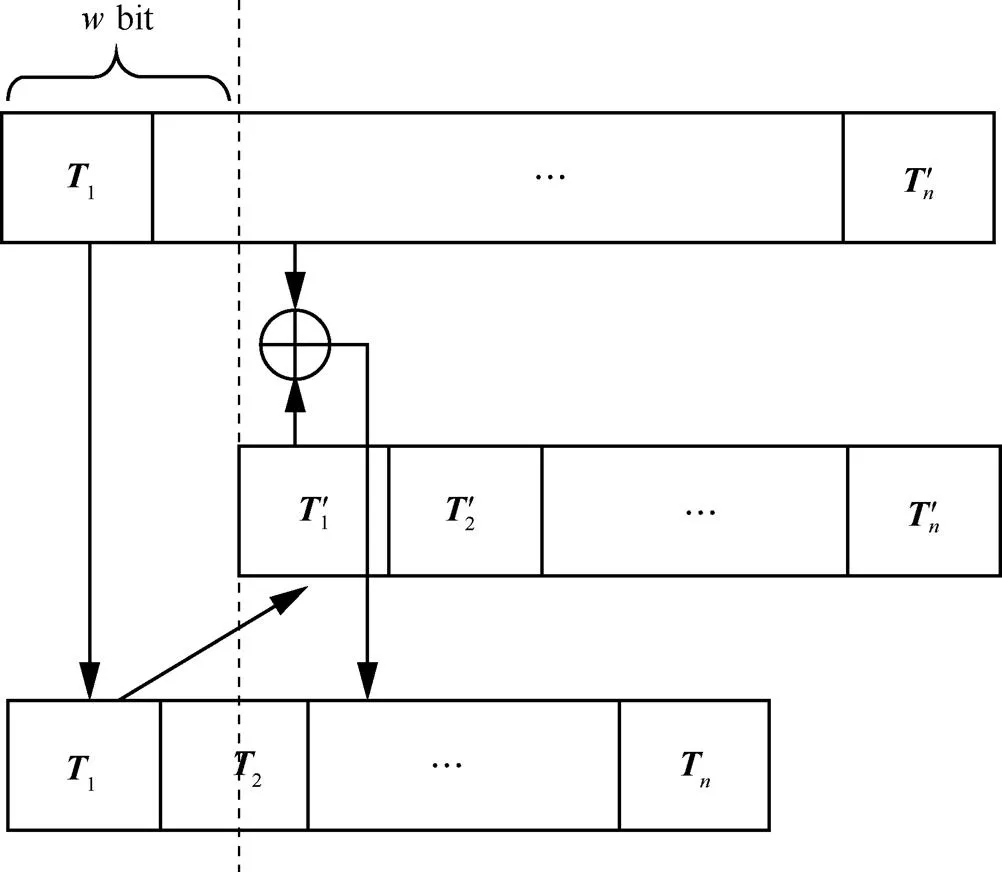
图5 双向可译码流的正向译码

2) 反向译码

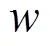
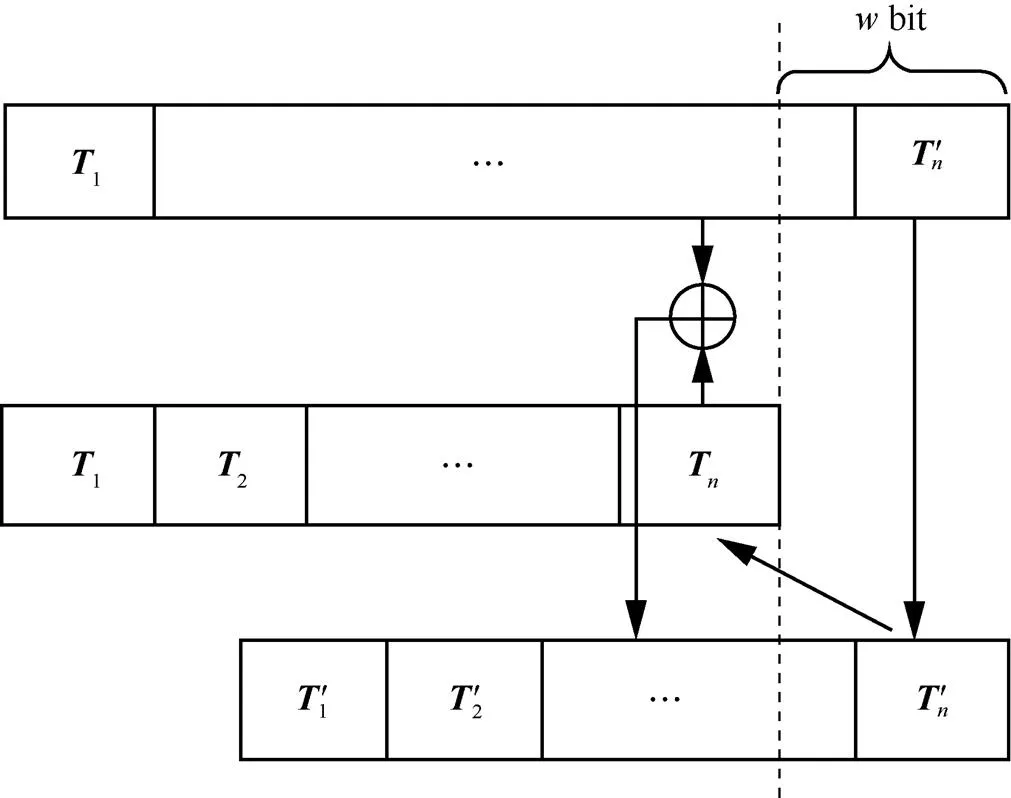
图6 双向可译码流的反向译码

3 仿真实验与分析

为了验证本文算法的性能，分别对独立同分布信源序列和图像这2种信源形式进行实验。仿真过程中的信道模型是AWGN信道，算术码编码器是MQ编码器[1]，通过参考开放代码“openjpeg”编写仿真实验程序。仿真实验是在主频为2.93 GHz 的PC上用C语言实现的。

3.1 离散无记忆信源

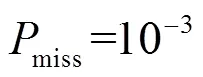
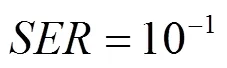
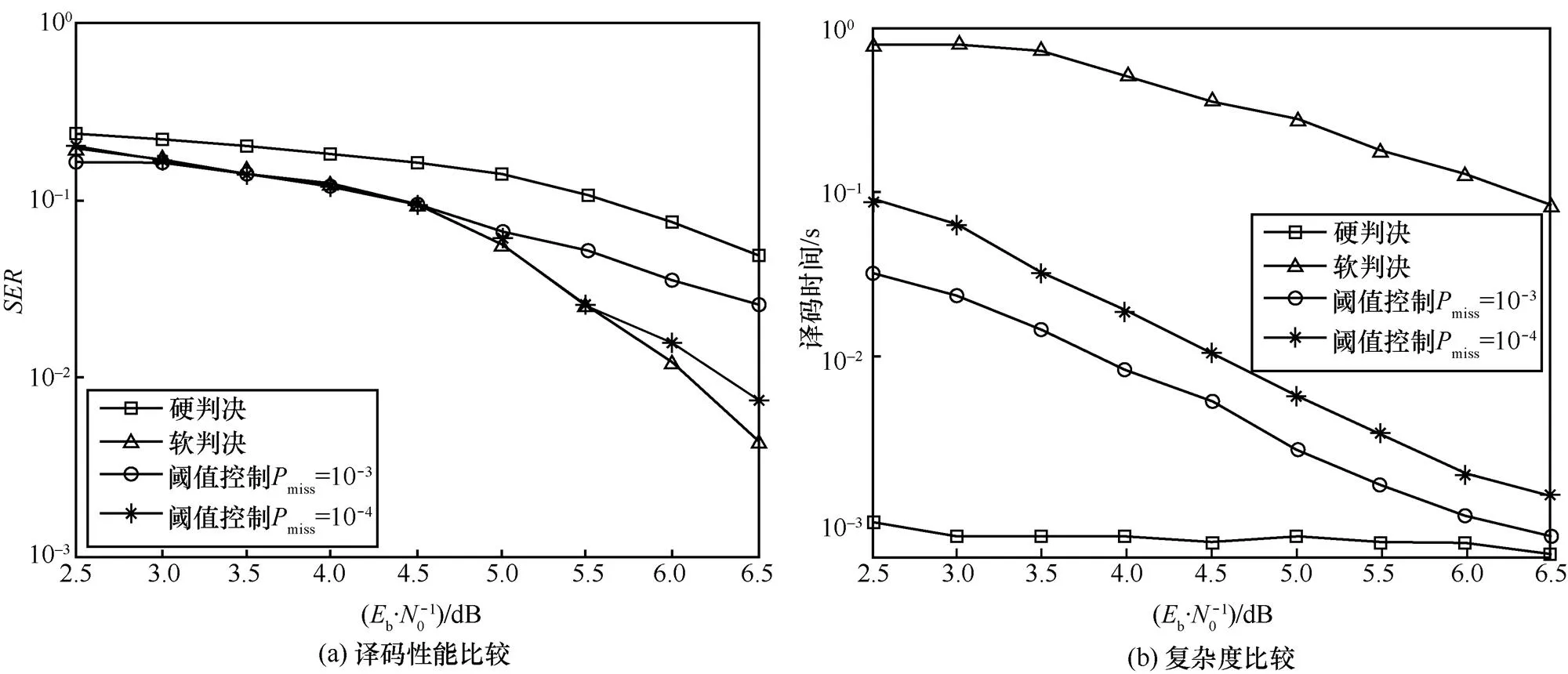
图7 各算法在相同条件下译码性能和复杂度比较

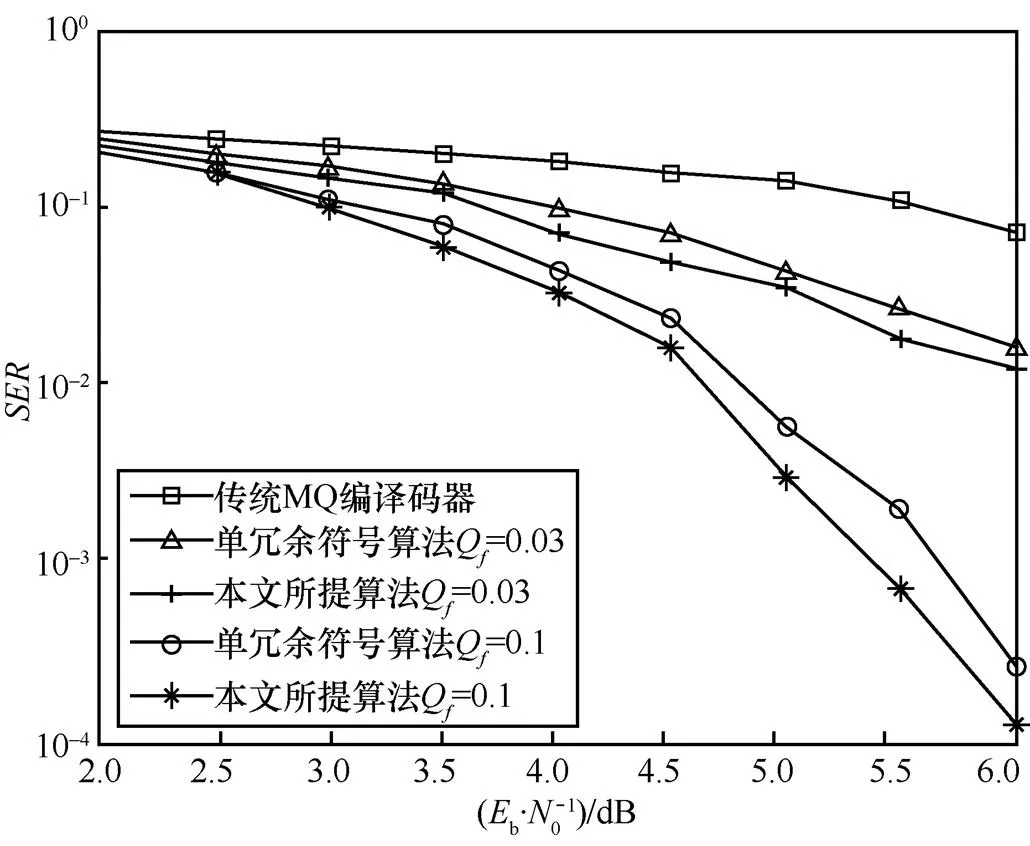
图8 各算法在不同冗余符号下误符号率比较

3.2 存在误码的图像译码

3.3 安全性

1) 密钥敏感性

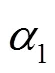
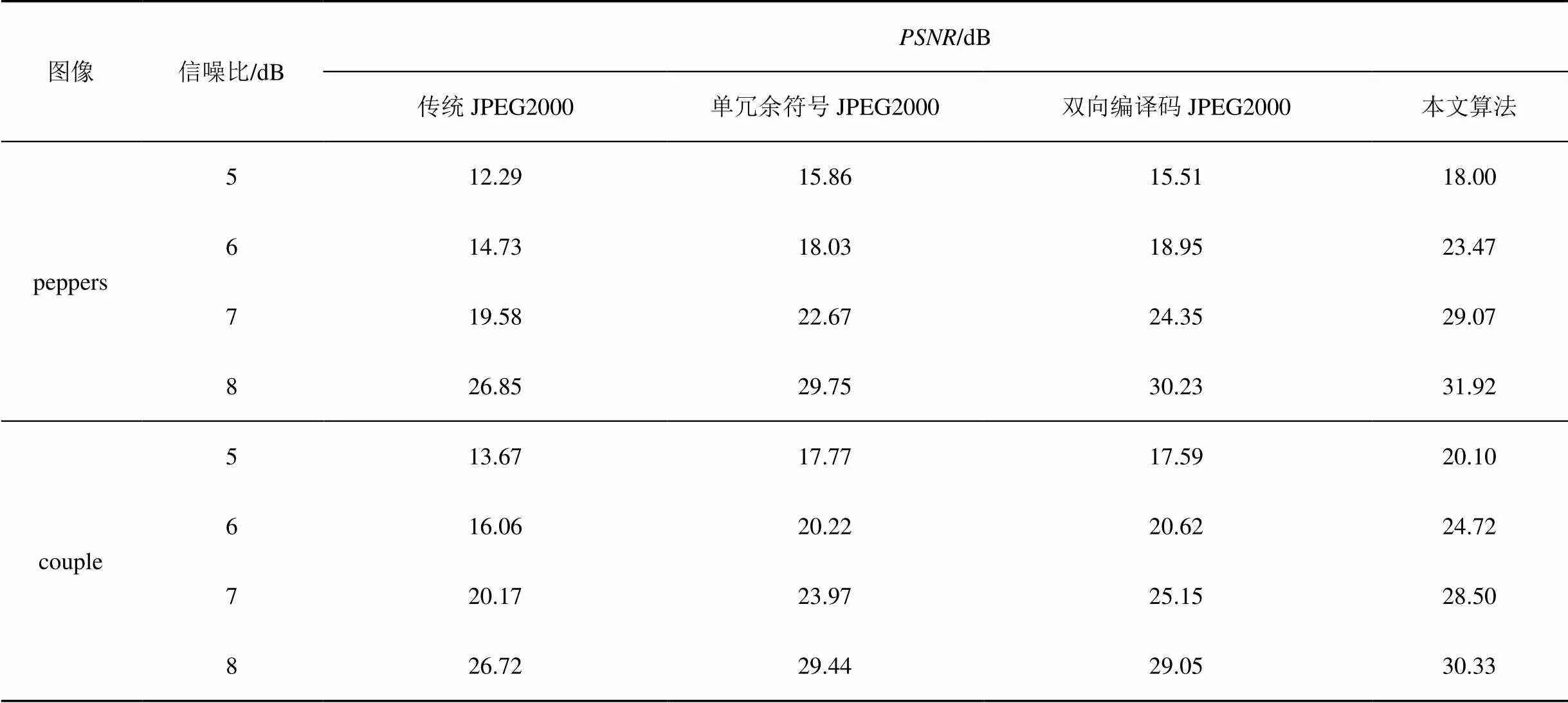
表1 各算法在不同信噪比下PSNR比较

2) 密钥空间

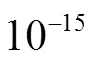
3) 抗差分攻击

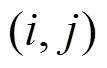
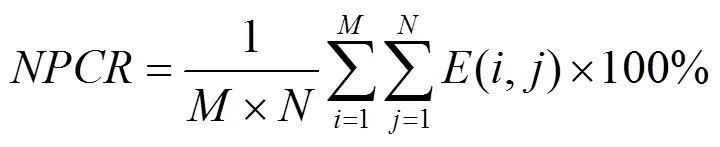
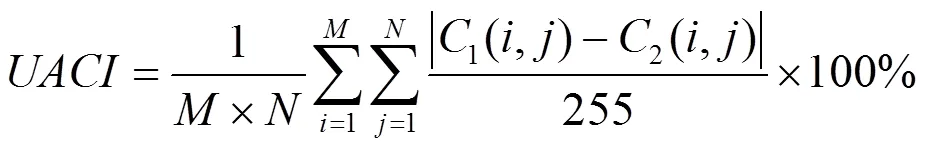
4) 统计特性

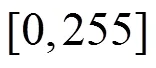
5) 加密时间和密文尺寸

对peppers图像采用文献[9]、文献[10]以及本文算法进行加密，并对比加密时间和密文尺寸，结果如表2所示。从表2可以看出，本文算法的密文尺寸远小于另2种算法，这是由于编码过程中不仅对明文进行加密，还进行压缩处理。同时，本文算法加密时所消耗的时间最少，也表明本文算法更适用于实际应用。

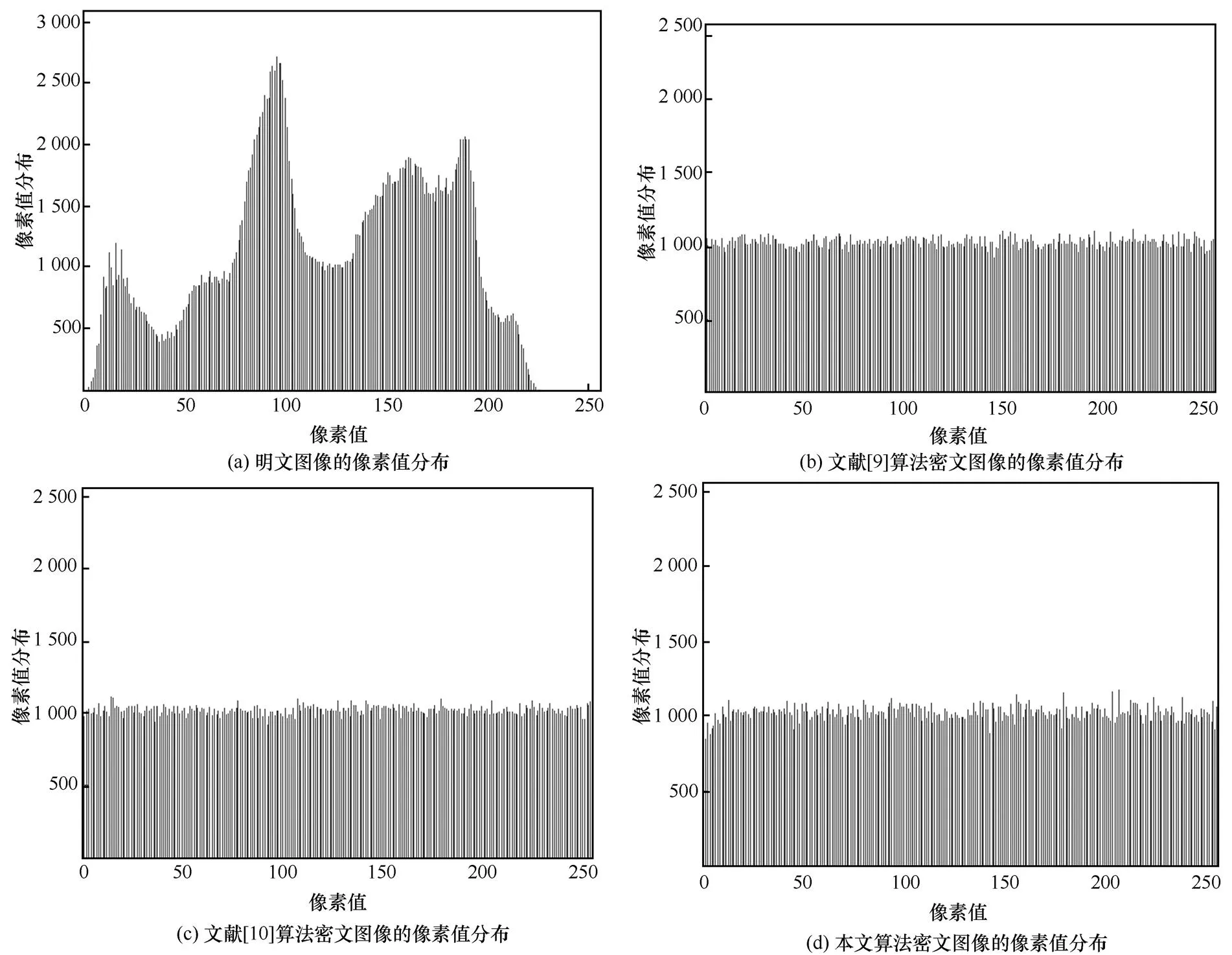
图9 peppers图像的直方图

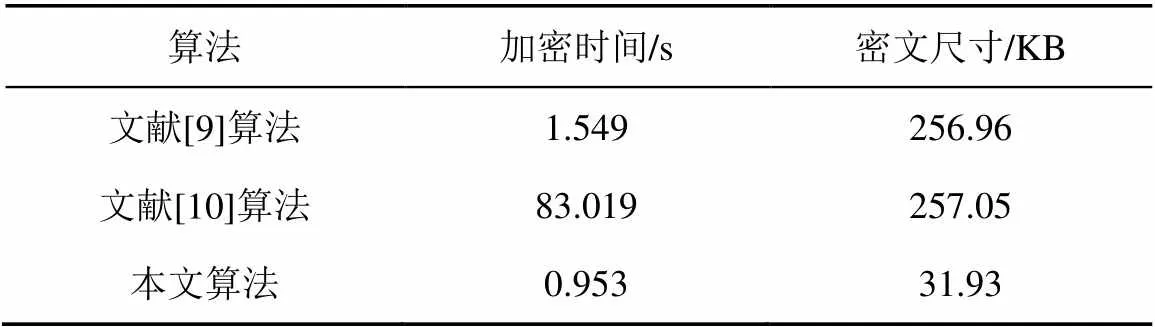
表2 各算法的加密时间和密文尺寸比较

4 结束语

本文提出一种基于混沌冗余和阈值控制的JPEG2000联合算术码双向编译码快速算法，编码时，在算术码编码模型中保留多个冗余符号，用混沌系统控制冗余符号的比例增强算术码编码的安全性；译码时，采用阈值控制和双向译码相结合，实现了基于最大后验概率的快速译码。仿真结果表明，所提算法降低了译码复杂度，提高了传输图像质量，具有良好的抗差错性和安全性。

[1] ISO/IEC 15444-1. Information technology-JPEG2000 image coding system-part 1: core coding system[S]. 2000.

[2] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3): 379-423.

[3] BOYD C, CLEARY J, IRVINE S, et al. Integrating error detection into arithmetic coding[J]. IEEE Transactions on Communications, 1997, 45(1): 1-3.

[4] GRANGETTO M, MAGLI E, OLMO G. Joint source/channel coding and MAP decoding of arithmetic codes[J]. IEEE Transactions on Communications, 2005, 53(6): 1007-1016.

[5] BI D S, HOFFMAN M W, SAYOOD K. State machine interpretation of arithmetic codes for joint source and channel coding[C]//Data Compression Conference. 2006: 143-152.

[6] ZEZZA S, MASERA G, NOOSHABADI S. A novel decoder architecture for error resilient JPEG2000 applications based on MQ arithmetic[C]//2014 IEEE International Symposium on Circuits and Systems, Melbourne. 2014: 902-905.

[7] GAO S S, TU G F. Robust H.263+ video transmission using partial backward decodable bit stream(PBDBS)[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2003, 13(2): 182-187.

[8] GAO S S, MA K K. Error-resilient H.264/AVC video transmission using two-way decodable variable length data block[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2010, 20(3): 340-350.

[9] MI B, LIAO X F, CHEN Y. A novel chaotic encryption scheme based on arithmetic coding[J]. Chaos Solitons and Fractals, 2008, 38(5): 1523-1531.

[10] WANG X Y, LIU C M. A novel and effective image encryption algorithm based on chaos and DNA encoding[J]. Multimedia Tools and Applications, 2016, 2016(2):1-17.

[11] 鄢懿, 张灿, 郭振永, 等. 基于混沌密钥控制的联合信源信道与安全算术码编译码算法[J]. 电子与信息学报, 2016, 38(10): 2553-2559.

YAN Y, ZHANG C, GUO Z Y, et al. Joint source channel and security arithmetic coding controlled by chaotic keys[J]. Journal of Electronics & Information Technology, 2016, 38(10): 2553-2559.

[12] ELABADY N F, MOUSSA M I, SABBEH S F. Improving the security of image encryption by using two chaotic maps[J]. International Journal of Computer Applications, 2014, 108(19): 27-32.

[13] SPITERI T, BUTTIGIEG V. Maximum a posteriori decoding of arithmetic codes in joint source-channel coding[J]. Communication in Computer and Information Science, 2012, 222(39): 363-377.

[14] LIN Q Z, WONG K W, LI M, et al. An effective error correction scheme for arithmetic coding[J]. Mathematical Problems in Engineering, 2015(2): 1-10.

[15] BRINDHA M, GOUNDEN N A. A chaos based image encryption and lossless compression algorithm using hash table and Chinese remainder theorem[J]. Applied Soft Computing, 2016, 40(1):379-390.

[16] 邓晓衡, 廖春龙, 朱从旭, 等. 像素位置与比特双重置乱的图像混沌加密算法[J]. 通信学报, 2014, 35(3): 216-223.

DENG X H, LIAO C L, ZHU C X, et al. Image encryption algorithms based on chaos through dual scrambling of pixel position an bit[J]. Journal on Communications, 2014, 35(3): 216-223.

Fast bidirectionally-decodable arithmetic coding withchaotic redundancy and threshold control

YAN Yi, TU Guofang, ZHANG Can, GAO Shaoshuai, CHEN Deyuan

School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101408, China

Although the JPEG2000 compression standard has high coding efficiency, its error resistance and security can’t meet the requirements of practical application. Based on this, a fast bidirectionally-decodable arithmetic coding method with chaotic redundancy and threshold control was proposed. At the encoder, the chaotic map controlled the probabilities of multiple redundant symbols to enhance the security of arithmetic coding. At the decoder, threshold control and bidirectional decoding were combined to realize fast decoding based on maximum a posteriori estimation. Simulation results show that the proposed method improves the reconstructed image quality with better error resistance and security.

secure error resistant arithmetic coding, chaotic map, threshold control, bidirectional decoding, JPEG2000

TN911.2

A

10.11959/j.issn.1000-436x.2018029

2017-01-10；

2018-01-19

凃国防，gft@ucas.ac.cn

国家自然科学基金资助项目（No.61571416, No.61271282）；中国科学院奖励基金资助项目（No.2017-06-17）

The National Natural Science Foundation of China (No. 61571416, No.61271282), Award Foundation of Chinese Academy of Sciences (No.2017-06-17)

鄢懿（1990-），女，江西景德镇人，中国科学院大学博士生，主要研究方向为联合信源信道与安全编译码。

凃国防（1954-），男，湖南长沙人，中国科学院大学教授、博士生导师，主要研究方向为联合信源信道编译码、无线通信、图像编码、信息安全和信号处理。

张灿（1954-），女，湖南长沙人，中国科学院大学教授、博士生导师，主要研究方向为移动无线通信、无线网络安全和信号处理。

高绍帅（1976-），男，山东德州人，博士，中国科学院大学教授、博士生导师，主要研究方向为无线通信、视频处理。

陈德元（1968-），男，贵州毕节人，博士，中国科学院大学副教授，主要研究方向为信道编码、联合信源信道编码。