基于压缩感知与矩阵补全技术的WSN数据收集算法

张策，李鸥，童昕，杨延平



基于压缩感知与矩阵补全技术的WSN数据收集算法

张策1，李鸥1，童昕2，杨延平3

（1. 信息工程大学信息系统工程学院，河南 郑州 450001；2. 61377部队，广东 深圳 518000；3. 清华大学电子系，北京 100084）

WSN无线链路不可靠，分组丢失现象普遍存在，且基于压缩感知（CS）数据收集算法对分组丢失十分敏感。首先，通过实验对分组丢失率和基于CS数据重构精度关系进行定量研究，提出极稀疏块观测矩阵，在降低每轮数据采集能耗的同时，也保持观测矩阵的近似低秩性质。其次，结合矩阵补全（MC）技术与CS技术，提出基于极稀疏块观测矩阵的压缩感知数据收集算法，在一个采集周期内进行数据收集，利用MC技术恢复丢失数据，减少分组丢失对数据收集的影响；利用CS技术重构全网数据，减少数据收集量，降低节点在数据收集时所需能耗，延长网络寿命。仿真分析表明，所提算法在分组丢失率小于50%的情况下能够保证高精度重构全网数据，抵抗不可靠链路。

无线传感网；数据收集；压缩感知；不可靠链路；矩阵补全技术

1 引言

WSN因传感器的低成本、小型化和低功耗等特点，在森林火灾监测、战场侦察等应用场景中具有巨大的应用前景。但由于传感网监测环境复杂、无线链路质量低、分组丢失率较高且单个节点能源受限等原因，使WSN仍受到诸多限制。

近年来，面向不可靠链路的传感网数据收集方法受到研究者的关注。文献[1]提出经典丢失数据补全算法——KNN（K-nearest-neighbor）算法，KNN简单地利用丢失数据的个最近邻居数据，估计丢失数据，算法复杂度低但精度差。文献[2]中提出的MSSA算法利用嵌入式自协方差矩阵，实现无参数和自适应数据恢复，被广泛应用于恢复地理数据。这些算法在仅有少量数据丢失的情况下有效，但在链路十分不可靠的传感网中，分组丢失率较高，此时，这些传统的数据恢复算法性能较差。

随着压缩感知（CS, compressive sensing）理论[3,4]的提出，一些研究者开始将CS应用于WSN数据收集，利用原始数据的空间相关性，有效地减少数据传输能耗，且具有天然的能耗均衡特性，能克服能量洞问题，延长网络寿命；基于压缩感知的数据收集算法具有数据重构过程复杂但压缩过程简单的特点、适合传感器节点低信息处理能力和能源受限的特点。文献[5]基于压缩感知，提出了CDG（compressive data gathering）算法，该算法利用数据的稀疏性和空间相关性，通过减少数据收集量有效地降低数据传输能耗。文献[6]将CS技术与最小路径树路由协议相结合，以降低整个数据传输路径上的能耗。文献[7]为了减少叶节点和距离叶节点较近的中间节点的通信量，提出了混合压缩感知（hybrid-CS）数据收集方法，仅对一部分通信量高的父节点使用压缩感知技术，减少网络数据通信量。文献[8]结合CS技术与Leach分簇路由，计算全网最优簇首个数，使簇首均匀分布于网络中，以减少网络能耗。

以上基于CS数据收集算法在链路可靠的情况下，均可有效降低网络能耗，且重构精度较高。但在实际传感网中，由于节点部署环境复杂和节点收发数据功耗限制等因素，导致无线链路质量低、网内分组丢失率高。在分布式压缩感知数据收集算法中，一个分组的丢失，会影响参与本次数据收集的所有节点，导致重构数据精度较低，重构数据无法使用。高分组丢失率使传统的基于CS的数据收集算法失效。文献[9]考虑了树型路由中不可靠链路对压缩感知的影响，所提算法设定参与数据收集的节点比例，在有分组丢失率的链路下，基于收到的数据分组构造观测矩阵，不观测发生分组丢失的节点，抵抗不可靠链路。但在该算法中，数据分组仍通过最短路由传输，能耗不均衡现象仍然存在。文献[10]在簇型路由中，针对轻负载下的链路不可靠，建立随机分组丢失模型，提出CS-NTSC（neighbor topology spatial correlation prediction based CS data gathering）算法，利用邻居拓扑矩阵预测丢失数据，减小错传的影响；针对重负载下的链路不可靠，建立节点伪失效模型，并提出CS-SSDG（sparse schedule for CS data gathering）算法，通过改变观测矩阵稀疏度，避免观测出错数据，弱化不可靠链路的影响。

矩阵补全（MC, matrix completion）技术是近几年新兴的一种技术，利用矩阵的低秩特性，恢复矩阵中丢失的数据，将MC技术应用于WSN数据收集，可以减少数据的采集量。文献[11]单一地利用MC技术压缩恢复数据，减少网络通信量，延长网络寿命；将MC数据恢复过程的NP-hard问题转化为可解的、复杂度低的最优化问题。但该算法没有分析真实数据的近似低秩性，且在树型路由下，网络能耗不均情况仍然存在。文献[12]结合CS和MC，利用MC补全数据传输时丢失的数据，利用数据的时间相关性进行CS数据压缩，达到抵抗不可靠链路、减少节点传输能耗的目的。但当网络数据采集周期长、网内受同一事件影响时，节点采集数据的时间相关性会很弱、空间相关性强，在时间上进行CS数据压缩，其恢复精度较低，且算法时间复杂度高。每个节点在采集完所有时隙的数据后进行数据处理传输，网络时延大。

为此，本文在无线链路不可靠条件下，对一个采集周期的数据，利用MC技术恢复因链路不可靠丢失的数据；利用节点的强空间相关性，对节点数据进行CS压缩，减少网络的数据传输量。本文主要贡献有以下3点。

1) 对一个时隙内的真实数据进行分析，实验证明数据具有近似低秩的性质，且收集一个时隙内数据，以降低网络时延。

2) 利用数据的低秩性质与空间相关性，将MC技术与CS技术相结合，提出极稀疏块观测矩阵，减小不可靠链路对数据重构的影响，在保证重构精度的前提下降低网络能耗。

3) 采用GreenOrbs系统真实数据，利用仿真软件Matlab对所提算法进行实验验证，实验结果表明所提算法在链路具有50%分组丢失率情况下，仍能保证高重构精度。

2 问题描述

2.1 基于压缩感知的分布式数据收集方法

网络采用簇型路由结构，整个网络划分为若干个簇，在每个簇内使用压缩感知技术进行数据收集，整个网络的拓扑结构示意如图1所示。

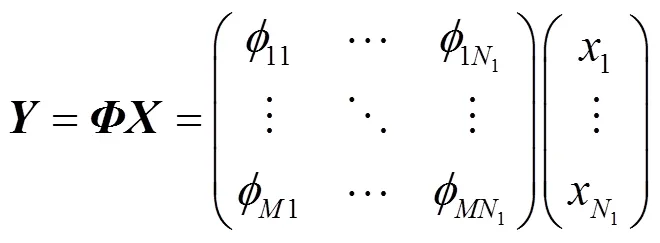
sink节点在收到观测向量后，通过求解凸优化问题，求解全簇的观测数据。

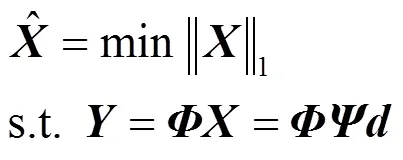
在数据传输过程中，由于复杂的监测环境、链路拥塞或冲突造成无线链路不可靠，存在一定的误码率与分组丢失率，对于误码率，当节点发生错传时，若接收节点通过信道译码无法恢复发生的错传位，接收节点将丢弃错传数据分组。本文假设节点一旦接收含错数据分组即丢弃，不进行纠错，因此，本文所假设的分组丢失率包含发生错传和丢失2种情况，节点未成功接收完整无错的数据分组即分组丢失。在簇型网络中，若节点的数据分组x丢失，则簇首得到的观测向量为

本文用归一化平均绝对误差（NMAE, normalized mean absolute error）衡量数据重构误差，即

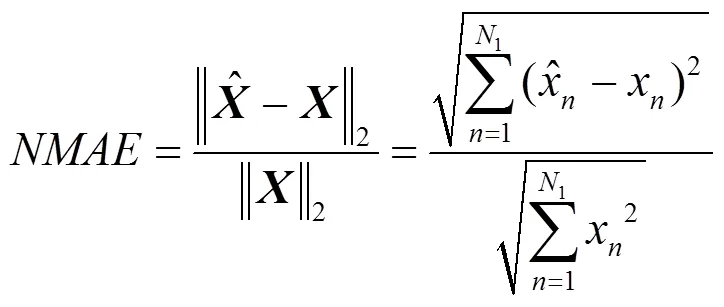
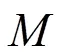
2.2 矩阵补全技术

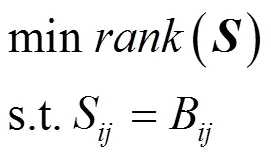
其中，，，指标集 。由于矩阵的秩函数是非连续、非凸的，求解式(5)是一个NP-hard问题，其求解复杂度呈指数级增长，最广泛的做法是将秩函数凸松弛到核范数，转换为凸优化问题，即

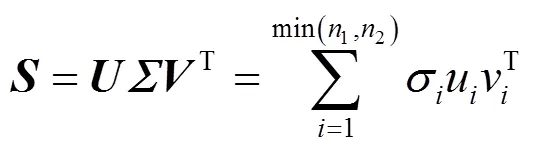
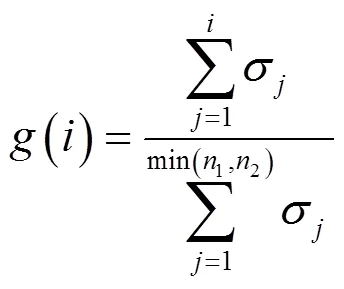
图3 矩阵低秩特性

实验结果表明，真实环境中传感器感知原始数据具有近似低秩的特征，若节点在数据传输的过程中丢失有一定数量的分组，即无线链路存在分组丢失率，可以利用原始数据矩阵的低秩性质，通过MC技术，恢复出丢失的数据分组，减少分组丢失对数据传输的影响。

由于传感网采集的数据阵为近似低秩矩阵，令

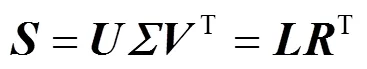
本文采用EDCA（efficient data collection approach）算法[11]求解式（10）。

3 算法设计

针对无线链路有分组丢失情况，提出基于极稀疏块观测矩阵的压缩感知数据收集算法（CS-SBM, CS data gathering algorithm based on sparsest block measurement matrix），结合MC技术与CS技术，在不重传的前提下，对一个采集周期数据进行数据收集，利用MC技术恢复丢失数据，减少分组丢失对数据收集的影响，利用CS技术重构全网数据，减少数据收集量，降低节点在数据收集时所需能耗，延长网络寿命。

3.1 极稀疏块观测矩阵

在簇内，成员节点根据存储的稀疏观测向量元素是否为0来判断是否参与本轮数据收集。在数据传输过程中若有分组丢失，则簇首收到的数据并不完整，此时可以利用MC技术恢复丢失数据。

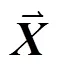
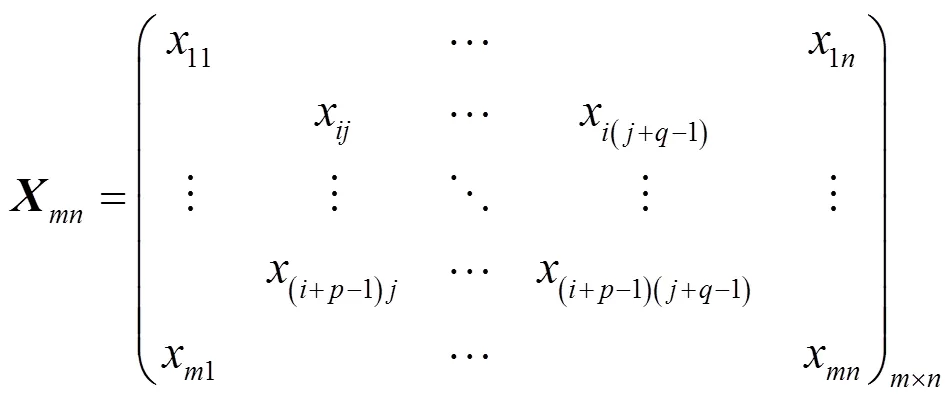
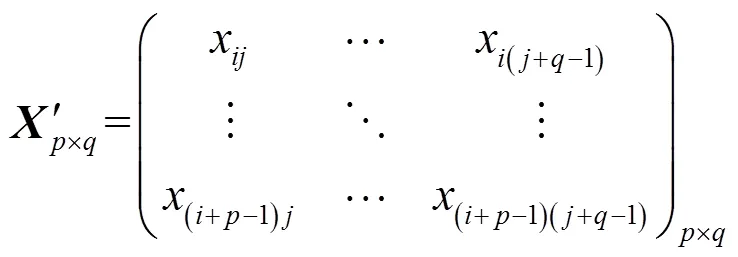
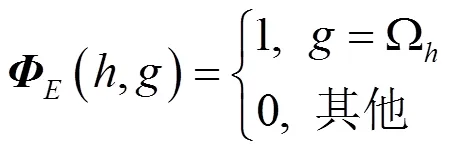
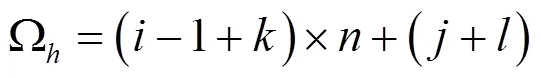
其中，表示的第列。SBM矩阵使每轮数据收集仅有一个节点参与，降低了数据采集能耗，且观测矩阵为全网原始矩阵的块矩阵，保持了矩阵的低秩性。

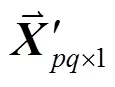
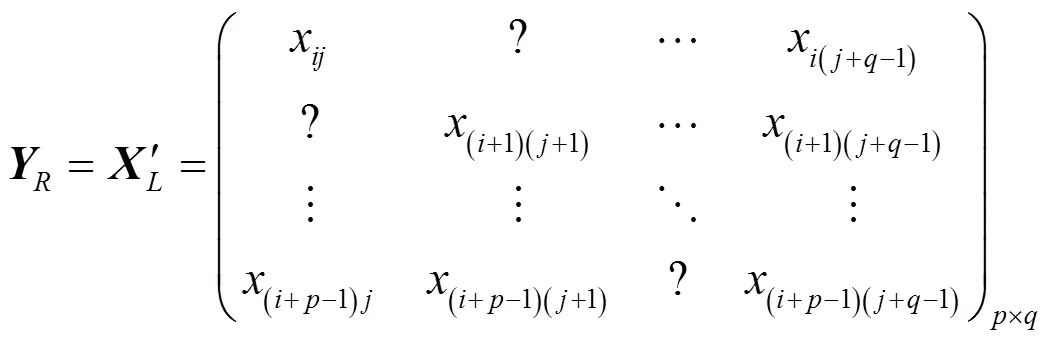
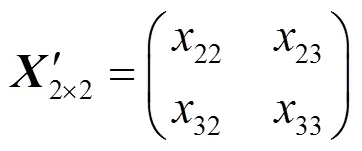
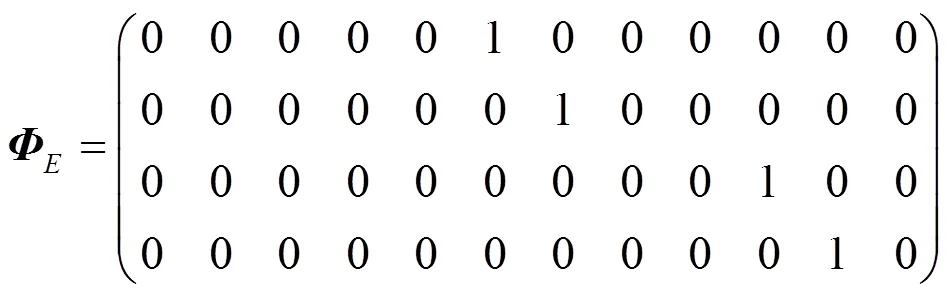
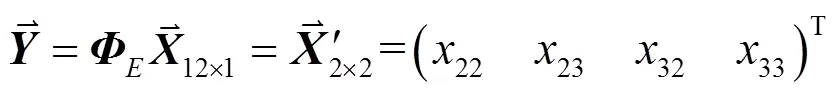
其簇首收到的观测向量的矩阵为

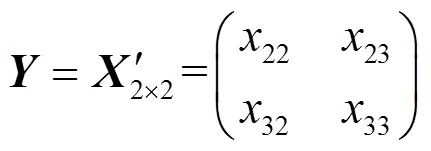
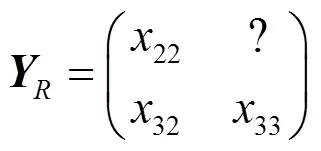
3.2 CS-SBM算法

CS-SBM算法流程如图5所示，具体步骤如下。

⑦ end for

⑧ end for

⑫ end for

图5 CS-SBM算法流程

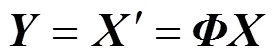
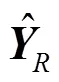
算法2 重构全网数据

4 仿真与分析

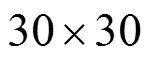
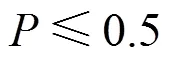
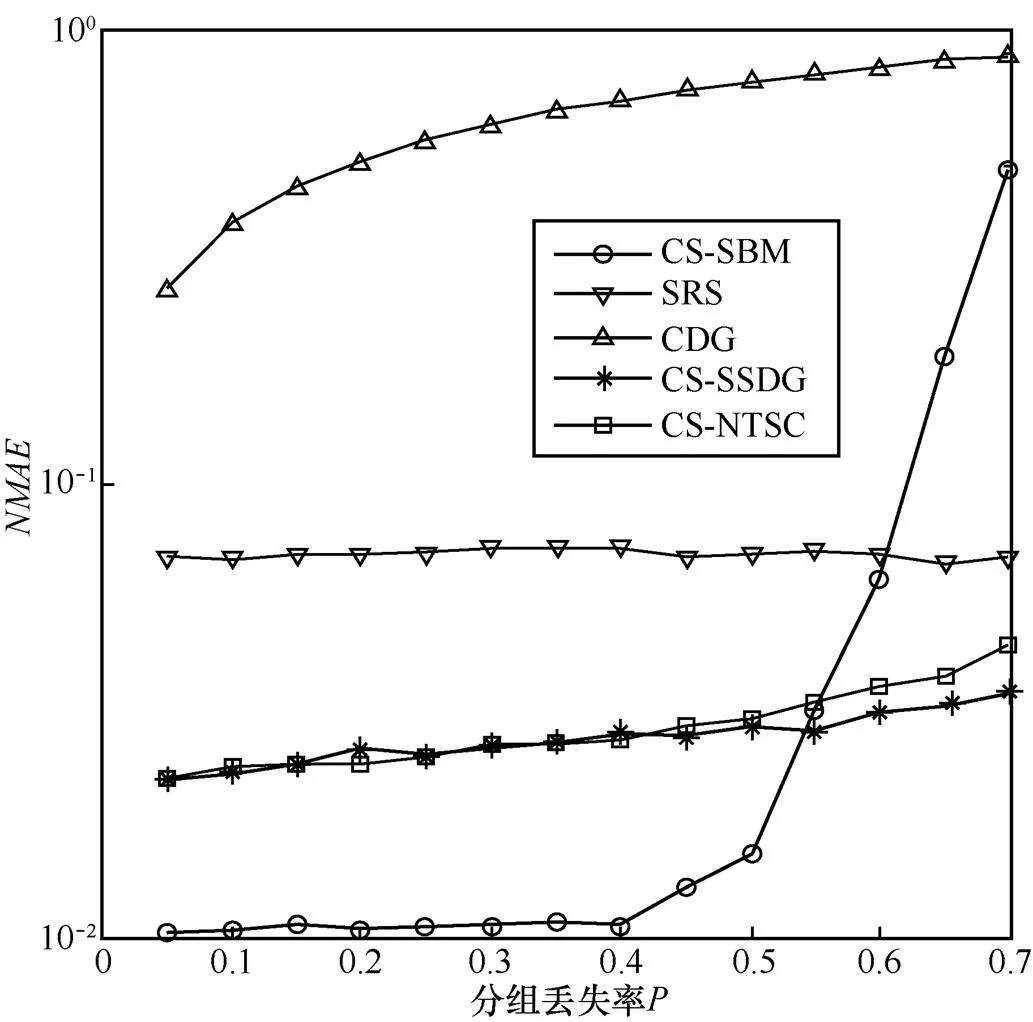
图6 CS-SBM算法性能（M=625）

表1 参数设置

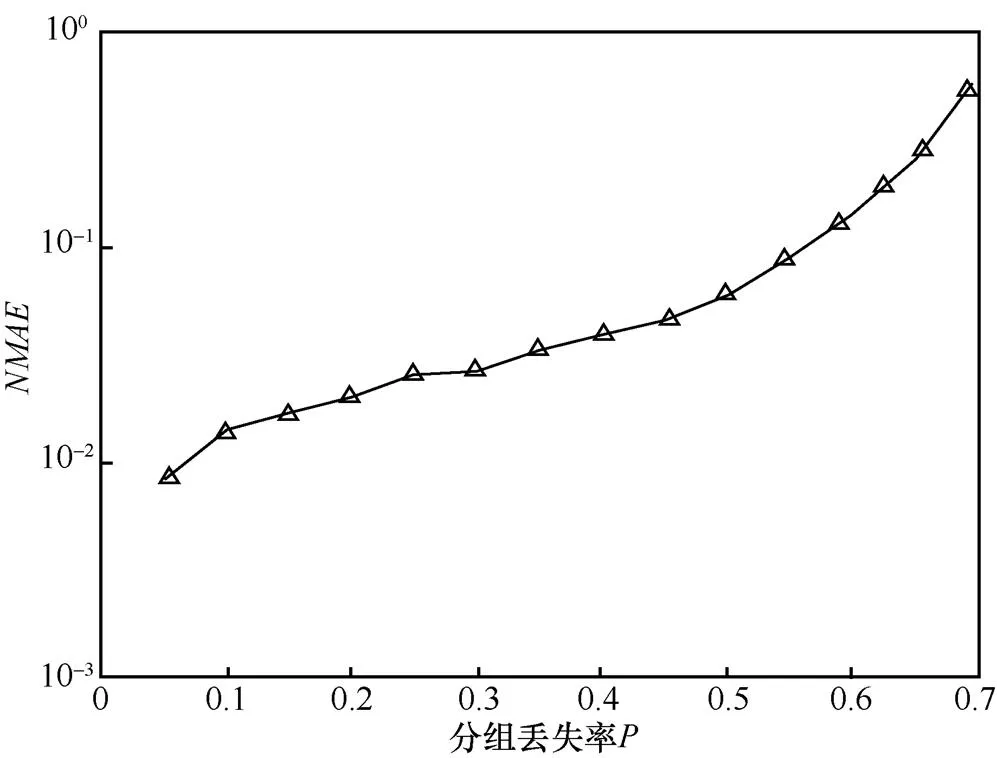
图7 MC恢复精度与分组丢失率关系

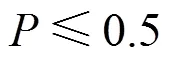
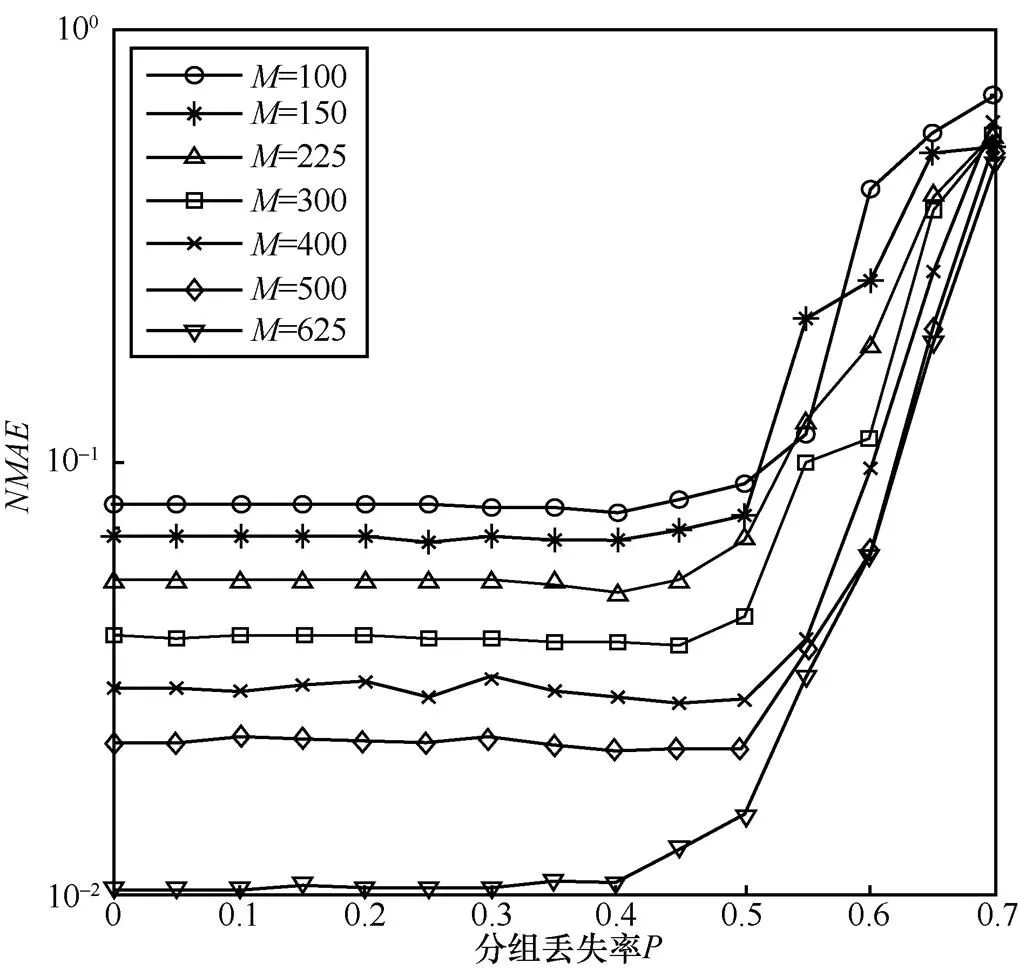
图8 不同观测次数下算法性能

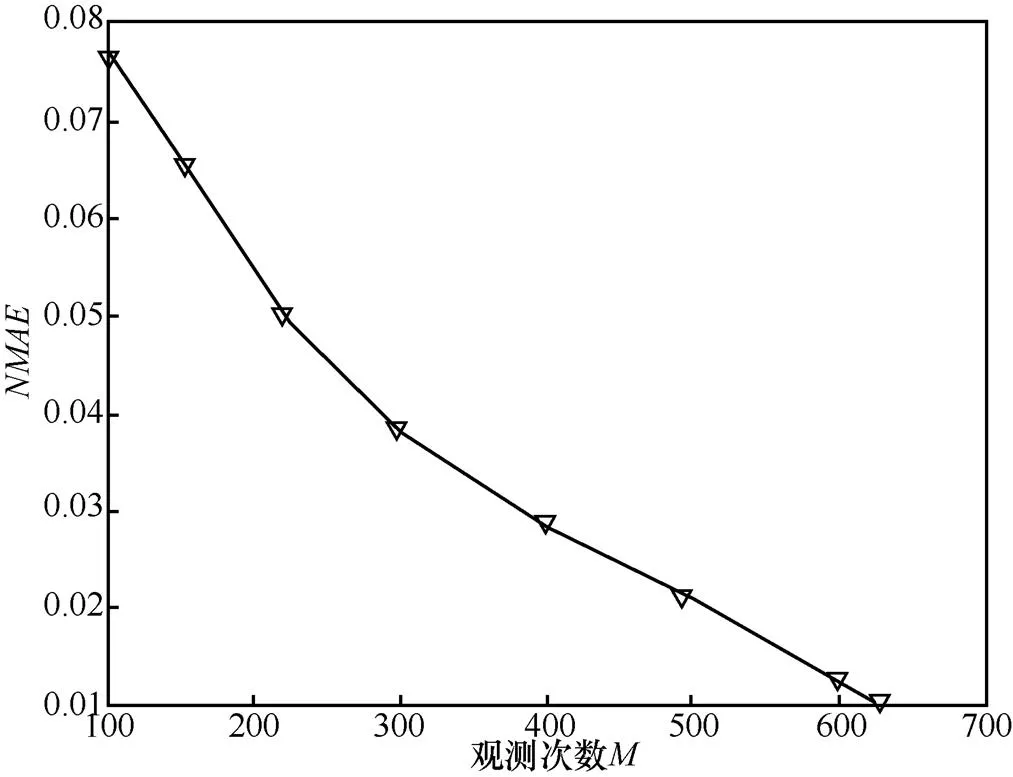
图9 观测次数与重构精度的关系（P=0.4）

5 结束语

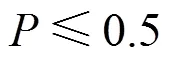
本文构造了SBM矩阵，并采用FFT基作为稀疏基，通过仿真实验可得，CS-SBM算法可以通过CS技术重构出全网数据，但并未理论证明SBM矩阵和FFT基满足RIP条件，如何从数学角度严谨地证明所提SBM矩阵满足RIP条件是下一步工作重点。

[1] COVER T, HART P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27.

[2] ZHU H, ZHU Y, LI M, et al. SEER: metropolitan-scale traffic perception based on lossy sensory data[C]//IEEE INFOCOM 2009. 2009: 217-225.

[3] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[4] BARANIUK R. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 56(4): 4-5.

[5] LUO C, WU F, SUN J, et al. Compressive data gathering for large-scale wireless sensor networks[C]//The 15th Annual Int Conf on Mobile Computing and Networking. 2009: 145-156.

[6] LUO C, WU F, SUN J, et al. Efficient measurement generation and pervasive sparsity for compressive data gathering[J]. IEEE Transactions on Wireless Communications, 2010, 9(12): 3728-3738.

[7] LUO J, XIANG L, ROSENBERG C. Does compressed sensing improve the throughput of wireless sensor networks?[C]//IEEE International Conference on Communications (ICC 2010). 2010: 1-6.

[8] WU X, XIONG Y, HUANG W, et al. An efficient compressive data gathering routing scheme for large-scale wireless sensor networks[J]. Computers and Electrical Engineering, 2013, 39(6): 1935-1946.

[9] WU X, YANG P, JUNG T, et al. Compressive sensing meets unreliable link: sparsest random scheduling for compressive data gathering in lossy WSN[C]//The 15th ACM Int Symposium on Mobile Ad Hoc Networking and Computing. 2014: 13-22.

[10] 张策, 张霞, 李鸥, 等. 不可靠链路下基于压缩感知的WSN数据收集算法[J]. 通信学报, 2016, 37(9): 131-141.

ZHANG C, ZHANG X, LI O, et al. Compressive sensing based data gathering algorithm over unreliable links in WSN[J]. Journal on Communications, 2016, 37(9): 131-141.

[11] CHENG J, JIANG H, MA X, et al. Efficient data collection with sampling in WSNs: making use of matrix completion techniques[C]// Global Telecommunications Conference. 2010: 1-5.

[12] FRAGKIADAKIS A, ASKOXYLAKIS I, TRAGOS E. Joint compressed-sensing and matrix-completion for efficient data collection in WSNs[C]//International Workshop on Computer Aided Modeling and Design of Communication Links and Networks. 2014: 84-88.

[13] CANDES E, RWCHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772.

[14] CHENG J, YE Q, JIANG H, et al. STCDG: an efficient data gathering algorithm based on matrix completion for wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(2): 850-861.

[15] LAKHINA A, PAPAGIANNAKI K, CROVELLA M, et al. Structural analysis of network traffic flows[J]. ACM SIGMETRICS Performance Evaluation Review, 2004, 32(1): 61-72.

[16] ZHANG Y, ROUGHAN M, WILLINGER W, et al. Spatio-temporal compressive sensing and internet traffic matrices[C]//ACM SIG COMM 2009 Conference on Data Communication. 2009: 267-278.

WSN data gathering algorithm based on compressivesensing and matrix completion technique

ZHANG Ce1, LI Ou1, TONG Xin2, YANG Yanping3

1. School of Information Systems Engineering, PLA Information Engineering University, Zhengzhou 450001, China 2. 61377 Unit, Shenzhen 518000, China 3. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China

The unreliable links and packet losing are ubiquitous in WSN. The performance of data collection algorithm based on compressive sensing is sensitive to packet losing. Firstly, the relationship between packet loss rate and CS-based reconstruction precision was analyzed, and the sparsest block measurement (SBM) matrix was formulated to keep the data gathering consumption smallest and make sure the low-rank property of measurements. Then, combined with the matrix completion (MC) and compressive sensing (CS), the CS data gathering algorithm based on sparsest block measurement matrix (CS-SBM) algorithm was proposed. CS-SBM gathered data in a period and recovered the loss data based on MC to weaken the impact of packet loss on data gathering. CS-SBM reconstructed data based on CS to reduce measurement number and energy consumption and prolong the network lifetime. Simulation analysis indicates that the proposed algorithm reconstruct the whole data with high-accuracy under 50% packet loss rate, resisting unreliable links effectively.

WSN, data gathering, compressive sensing, unreliable link, matrix completion technique

TP393

A

2017-10-12；

2018-01-17

童昕，tongrour@foxmail.com

国家科技重大专项基金资助项目（No.2016zx03001010）

The National Science and Technology Major Project of China (No.2016zx03001010)

10.11959/j.issn.1000-436x.2018034

张策（1991-），男，四川南充人，信息工程大学博士生，主要研究方向为无线自组织网络、无线传感网与路由协议。

李鸥（1961-），男，陕西宝鸡人，博士，信息工程大学教授、博士生导师，主要研究方向为无线传感网、认知无线电网络与无线自组织网络。

童昕（1990-），女，湖北黄冈人，61377部队助理工程师，主要研究方向为多天线信号联合处理。

杨延平（1986-），男，河南平顶山人，清华大学博士后，主要研究方向为无线认知通信、网络编码、自适应调制。