一个非线性带分布时滞尺度结构的种群模型正稳态解的存在性*
柏萌,冯兆永,周庆华
(1. 广东省肇庆学院数学与统计学院,广东 肇庆 526061;2. 中山大学数学学院,广东 广州 510275)
本文研究如下带分布时滞的具有尺度结构的非线性的种群模型:
(1)

对于0≤x≤m
(2)
问题(1)是一个带分布时滞的具有尺度结构的非线性的种群模型。在问题(1)中,既考虑新生个体的产生过程中需要的不可少的时间间隔,又考虑种群内部竞争的影响。确切的说,问题(1)的分布时滞表示的是怀孕到生产或者产卵到孵化的时间间隔,这个时间间隔可以从0变到τ(参见文[1-5]),而且生长率γ、死亡率μ和繁衍概率β都与较小尺度种群和较大尺度种群的总密度相关。类似问题(1)的线性的带分布时滞的具有尺度结构的种群模型的全局解的适定性和解的渐近性态已在文[2]得出。问题(1)正的全局解的存在性已在文[4]得出。本文将研究问题(1)正稳态解的存在性。对于非线性的种群发展方程,正稳态解(即与时间无关的解)的存在性是很重要的问题,近年来不少学者用不同的方法研究了一系列非线性的不带时滞的种群发展方程的正稳态解的存在性[6-9]。文[6]用计算的方法研究了一个非时滞的带尺度结构的种群模型的正稳态解的存在性。文[7-9]用算子半群的方法研究了一些非时滞的带年龄结构或者尺度结构的种群模型的正稳态解的存在性。本文主要利用文[7]和文[9]的算子半群方法,研究问题(1)的正稳态解的存在性,由于此问题是带分布时滞的,需要一些改进,主要的改进在将问题(1)这个带分布时滞的种群模型正稳态解的存在性问题转化为巴拿赫空间上的柯西问题正稳态解的存在性问题。
本文对生长率γ、死亡率μ和繁衍概率β的假设如下:

(H2)γ∈C([0,m]×[0,+∞)×[0,+∞)),存在常数γ0>0,使得对于所有的x∈[0,m],N1∈[0,+∞)和N2∈[0,+∞),都有γ(x,N1,N2)≥γ0。γ对于x存在一阶偏导数γx∈C([0,m]×[0,+∞)×[0,+∞)),并且存在常数γ1>0,使得对于所有的x∈[0,m],N1∈[0,+∞)和N2∈[0,+∞),都有|γx(x,N1,N2)|≤γ1。
(H3)β∈C([-τ,0]×[0,m]×[0,m]×[0,+∞)×[0,+∞)),β≥0,并且当y>x时,β(·,x,y,·,·)>0。
1 问题转化
本节将问题(1)正稳态解的存在性问题转化为巴拿赫空间上的柯西问题正稳态解的存在性问题。可在文[1-3]中找到相似的转化方法。
引入如下巴拿赫空间:
XL1[0,m], 其模为
X1L1[0,l], 其模为
X2L1[l,m], 其模为
Y{u∈W1,1(0,m):u(0)=0},其模为
EL1([-τ,0],X)
其模为

A(V1,V2)u(-γ(·,V1,V2)u)′对于u∈X;
B(V1,V2)u-μ(·,V1,V2)u对于u∈X;Φ(V1,V2)对于
对于给定的v∈X,有A(V1,V2)∈L(Y,X),B(V1,V2)∈L(X)和Φ(V1,V2)∈L(E,X)。 利用以上记号,将问题(1)重新写为巴拿赫空间X上的延迟微分方程的初边值问题:
(3)
此处n:[0,+∞)→X定义为n(t)n(t,·);nt:[-τ,0)→X定义为nt(σ)n(t+σ),σ∈[-τ,0],而且

接下来, 引入巴拿赫空间E上如下算子:

D(G)=W1,1([-τ,0],X),
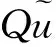
注意到G∈L(D(G),E)且Q∈L(D(G),X)。 令
X

Y
W1,1([-τ,0],X)×W1,1(0,m),

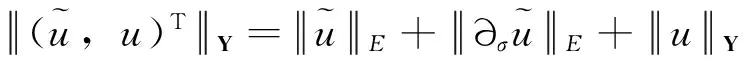
定义算子A(V1,V2):Y→X:
A(V1,V2)U
对于


利用以上记号,将问题(3)重新写为巴拿赫空间X的柯西问题:
(4)
此处


于是问题(1)的正稳态解的存在性问题,可以转化成如下问题解的存在性问题:
(5)
对于
2 正稳态解的存在性
本节首先考虑β可以分离的特殊情况,即
β(σ,x,y,N1,N2)=β1(x)β2(σ,y,N1,N2)
或者
β(σ,x,y,N1,N2)=β3(x,N1,N2)β4(σ,y)
或者
β(σ,x,y,N1,N2)=β5(x,N1)β6(σ,y,N2)
或者
β(σ,x,y,N1,N2)=β7(x,N2)β8(σ,y,N1)
利用文[7]中的定理2.5给出以上情况下问题(5)有解的充分条件。然后再用文[9]中的算子扰动的方法给出β为一般情况下问题(5)有解的充分条件。
这里以
β(σ,x,y,N1,N2)=β1(x)β2(σ,y,N1,N2)
或者
β(σ,x,y,N1,N2)=β3(x,N1,N2)β4(σ,y)
为例, 其余的特殊情况的分析过程和结论类似。给出以下假设(H4)和(H4)′:



(P1) 当(U1,U2)=(0,0)时,s(A(U1,U2))>0;



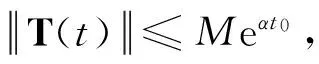

其中
Eλ(x,U1,U2)=

(λI-A(U1,U2))U=0

上述方程的解为
上式两边分别乘上eλσβ2(σ,x,U1,U2),然后分别对x和σ从0到m和-τ到0积分,可得
于是可知,λ∈C是线性算子A(U1,U2)的特征值当且仅当λ是特征方程K(U1,U2)(λ)=1的解。


定理1假设条件(H1)-(H4)成立, 并且
则问题(5)有解。

定理2假设条件(H1)-(H3)以及(H4)′成立,并且
则问题(5)有解。
证明同定理1(略)。
接下来给出β为一般情况下问题(5)有解的充分条件。
定理3假设条件(H1)-(H3)以及以下的两个假设条件成立:
而且
(H6) 存在
使得
σ∈[-τ,0],x,y∈[0,m]
而且
则问题(5)有解。

定理4假设条件(H1)-(H3)以及以下的两个假设条件成立:
σ∈[-τ,0],x,y∈[0,m]
而且
则问题(5)有解。
证明同定理3(略)。
根据β的分离情况还可以提出类似定理3和定理4的充分条件, 这里不一一累述。
参考文献:
[1]PIAZZERA S, TONETTO L. Asynchronous exponential growth for an age dependent population equation with delayed birth process [J]. J Evol Equ, 2005, 5(1): 61-77.
[2]BAI M, XU S. On a size-structured population model with infinite states-at-birth and distributed delay in birth process [J]. Applicable Analysis, 2013, 92(9): 1916-1927.
[3]柏萌,冯兆永,徐士河,等. 带分布时滞的具有尺度结构的种群模型的平衡指数增长[J], 中山大学学报(自然科学版), 2014, 53(1): 22-27.
BAI M, FENG Z Y, XU S H, et al. Balanced exponential growth for a size-structured two-phase population model with delayed birth process [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2014, 53(1): 22-27.
[4]BAI M, XU S. Global existence of solutions for a nonlinear size-structured population model with distributed delay in the recruitment [J]. International Journal of Mathematics, 2015, 26(10): 1550085-1-20.
[6]KATO N. Stationary solutions to a system of size-structured populations with nonlinear growth rate [J]. Journal of Biological Dynamics, 2012, 6 (Suppl 1): 42-53.
[8]FARKAS J Z, HINOW P. Steady states in hiererchical structured populations with distrbuted populations at birth [J]. Discrete & Continuous Dynamical Systems-Series B, 2013, 17(8): 2671-2689.
[9]FARKAS J Z, GREEN D W, HINOW P. Semigroup analysis of structured parasite populations [J]. Mathematical Modelling of Natural Phenomena, 2010, 5(3): 94-114.
[10]ENGEL K J, NAGEL R. One-parameter semigroups for linear evolution equations [M]. New York: Springer, 2000.

