雾霾天气下图像增强算法的研究

李浪，张爱萍

（西安建筑科技大学，西安 710055）

0　引言

近年来，环境问题日趋严重，在重度雾霾天气条件下，监控系统所采集到的图像饱和度差、对比度低，无法满足人们的需求。因此，研究雾霾等极端天气对数字图像的影响以及对图像进行清晰化处理，已成为图像去噪的一种趋势。目前国内外对图像去雾霾算法的研究主要分为基于模型的图像复原方法和非模型的图像增强方法[1]，其中基于模型的图像复原方法通常是针对雾霾天成像的光学模型，在场景的深度信息已知的条件下，通过反推成像过程，还原出无雾情况下的场景信息，达到图像去雾的目的，因而需要通过多幅图像或者辅助信息进行去雾处理[2]，因此对于单幅图像，在缺少辅助信息的情况下，这类方法并不适用。而非模型的图像增强方法[3-5]主要是通过增强降质图像的对比度来突出图像中的细节信息的，从而达到清晰化图像的目的，文献[3]提出基于高斯加权函数的直方图规定化的图像去雾算法，该算法能够增强图像的局部细节，但雾霾信息的去除不够明显。文献[4]提出的同态滤波的图像增强方法可以很好地去除图像的雾霾信息，但是它也会在一定程度上造成原有图像细节信息的丢失。文献[5]提出一种基于小波变换的雾霾天阈值确定模型，能够较好地增强图像细节信息，但阈值的二值化性决定了图像必定会失真。同态滤波和小波变换都是典型的非模型的图像增强方法，能够增强图像的对比度，通过减少低频成分，增加高频成分，实现滤波去噪的目的。但同态滤波在锐化图像边缘的同时不可避免的造成低频信息的丢失。小波变换是一种多分辨率的分析方法，它将原始图像分解成不同的分辨率，使其具有代表信号在频域和时域的局部特征的能力，因此通过小波重建可以有效的改善处理后的图像质量。本文结合小波分析和同态滤波的优点，将含有雾霾信息的图像经小波分解成高频带和低频带，对高频子带采用非线性增强的方法，提高图像的细节信息，低频子带采用同态滤波的方法来去除雾霾信息，实验结果表明小波重构后的图像清晰度有明显提升。

1　经典的同态滤波算法和小波分析算法

1.1　经典的同态滤波算法

同态滤波是一种把数字图像的灰度变换和频率过滤相结合的图像处理方法[6]。依据“照度—反射”图像生成的模型，一幅完整的图像 f(x,y)可以表示为入射分量i(x,y)和反射分量r(x,y)乘积的形式，关系如下：

其中 i(x,y)∈(0,∞)，r(x,y)∈(0,1)。

由于入射分量取决于外界光源照射在物体上的能量强度，表示了景物的照明，一般变化缓慢，在频域中表现为低频成分；而反射分量取决于物体表面的反射率，表示了景物的细节，因此在频域中表现为高频成分。

由于两个函数乘积的傅立叶变换是不可分的，因此将其转为对数域中进行运算，对式（1）取对数运算有：

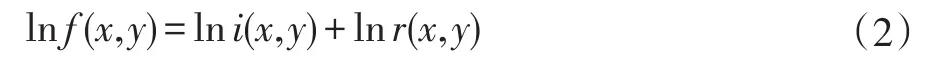
从而将（1）式的乘性分量变为加性分量。对（2）式两端进行快速傅立叶变换（FFT），则有：

其中，F(u,v)、I(u,v)和 R(u,v)分别为 lnf(x,y)、lni(x,y)和lnr(x,y)的傅立叶变换。该式表明，通过上述方法可以将入射分量的频谱与反射分量的频谱分离开，因而通过求解这两个分量就可以得到增强的图像。

设计一个同态滤波函数H(u,v)，使得在对数域中衰减频谱的低频部分，增强高频部分，从而衰减图像的入射分量并增强反射分量，用此滤波函数对（3）式进行处理，得到：

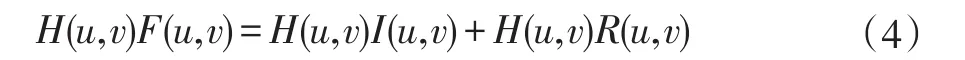
滤波后，对上式进行傅立叶反变换（IFFT），就可从频域转换到空间域有：

对式（5）进行指数变换，得到经过同态滤波后的图像：

对于雾霾图像，雾霾信息通常变化缓慢，在频率域中通常集中在低频部分，而有效的图像信息对应于高频部分，因此，削弱低频信息或者增强高频信息可以有效的增强图像的对比度。选用合适的同态滤波函数可以实现对这些分量的理想控制。

通常同态滤波的滤波效果与滤波传递函数H(u,v)的选择有关，同态滤波函数如图1所示：

图1中，H(u,v)为同态滤波函数，γH代表的是高频增益，γL代表的是低频增益，D(u,v)表示为频率(u,v)到滤波中心(u0,v0)的距离，其数学表达式为：

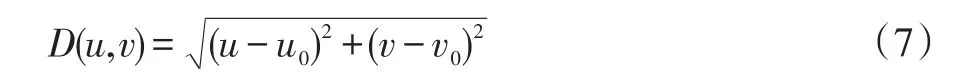
对于雾霾天气下受光照不均匀干扰的图像，采用n阶巴特沃斯高通滤波器作为同态滤波函数，表达式为[4]：

其中，D0表示截止频率。一幅M×N的图像D0的计算公式为：

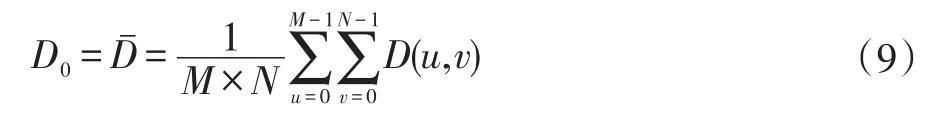
选择好合适的参数可以减小低频和增加高频，从而使得图像的对比度增强。本文在后面的部分采用同态滤波对雾霾天气下的图像进行增强，并对其结果进行了分析。

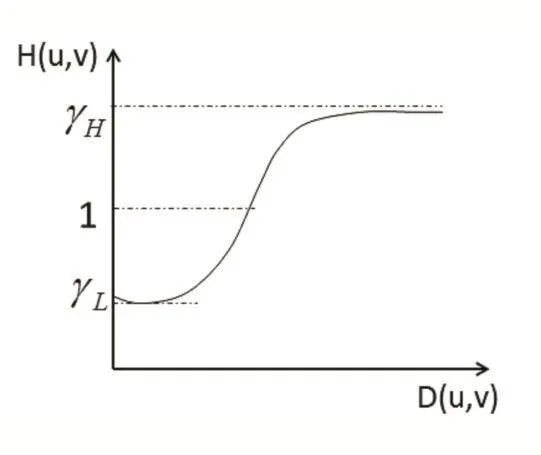
图1　同态滤波函数曲线

1.2　经典的小波分析算法

同态滤波中，傅立叶变换采用的是一种全局的变换思想，它可以将信号从时域完全转换到频域，因此它无法表达出信号同时在时域和频域的区域特性。小波变换是一种时间—尺度分析方法，具有多分辨率分析的特点，而且在时域和频域都有着很好的局部化特性[7]，因而被广泛应用于图像处理领域。

小波变换中各个层次分别对应于不同的频率和分辨率，相应的小波逆变换可以完成图像的精确重构[8]。一维小波变换可以通过张量积推广到二维图像的情况，也就是分别对图像的水平和垂直方向进行小波变换。根据Mallat快速分解算法，一幅大小为M×N的图像 f(x,y)可以表示为[9]：

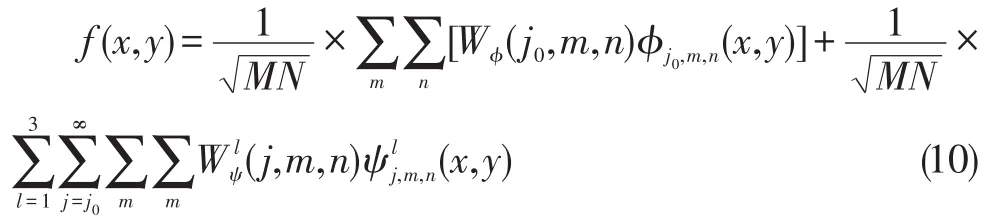
式中，j0为任意开始的尺度，通常情况下取 j0=0，Wϕ系数为 f(x,y)在尺度 j0处的近似，对于 j＞j0，系数附加了水平、垂直和对角方向上的细节，ϕ（x,y)和ψ（x,y)分别为二维小波函数和尺度函数。

对含有雾霾信息的原始图像经过一级小波分解，可以得到高频细节图像cH1，cV1，cD1和一个低频近似图像cA1，仅对低频子带cA1进行二级的小波分解得到cH2，cV2，cD2和cA2，依次进行可以得到多级的小波分解 cHi，cVi，cDi（i=1,2,...,τ）和 cAτ。可以选择一个适合的分解级数τ，使图像因雾霾而引起的噪声主要体现在cAτ低频区域的小波系数中。图2为三层小波分解的示意图：

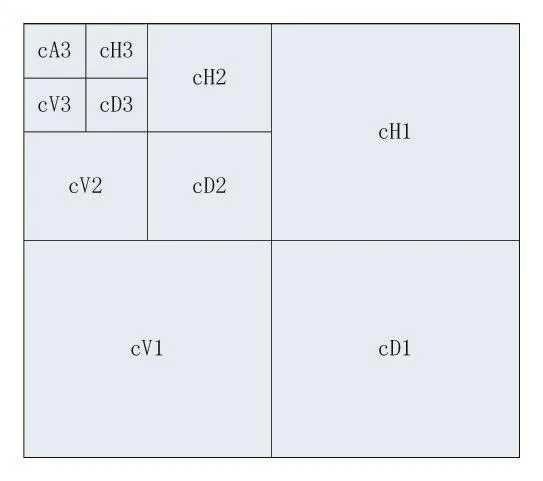
图2　三层小波分解的示意图

图像经过二维离散小波分解后，高频部分体现了图像的细节特征,由于低频部分集中了绝大部分能量，因此反映了图像的整体面貌。通常情况下，按照一定的规则来修改各个分解级的小波系数，然后做相对应的小波逆变换就可得到处理后的图像。本文采用文献[10]中小波系数的非线性增强方法来实现雾霾天的图像增强效果，小波系数的变换函数为：

其中a和b都是正实数，a决定了其整体增益的幅度，b则决定了各个分解级之间的幅度差。

2　雾霾天气下图像增强算法设计

在雾霾天气条件下，监控系统所采集到的图像饱和度差、对比度低，为了能够在有效去雾的同时保留图像的整体面貌，提高图像的整体对比度，本文提出如图3的图像增强过程。该方法结合小波分析和同态滤波方法各自的优点，高频带用非线性增强增加图像的细节信息，低频区用同态滤波和对比度拉伸的方法去除雾霾信息，小波重构后的图像为去霾后清晰的图像。

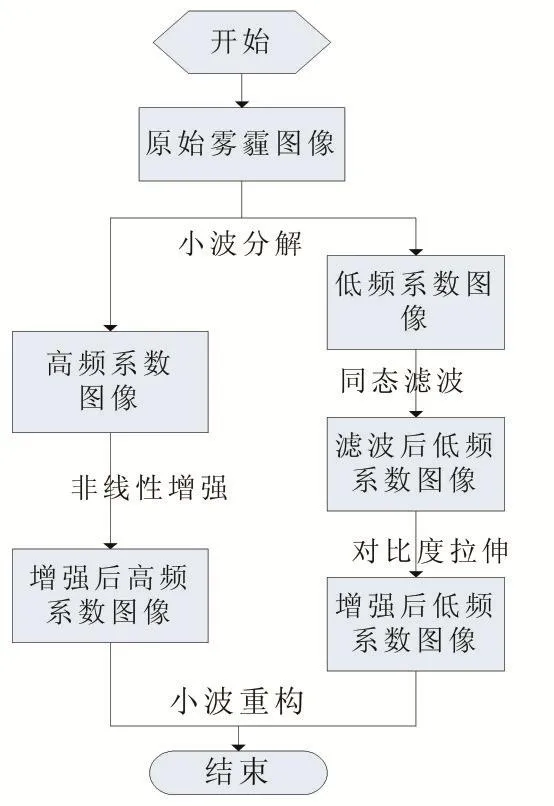
图3　雾霾图像的增强过程

从频谱分析的角度来讲，小波变换的结果是原始信号在一系列倍频程划分的频带上的多个高频带和一个低频带[8]。I.M.Johnstone等人证明了平稳相关噪声的小波变换在每一个分辨率层的各个子带上仍是平稳的[11]，因此可以对各个分辨率下的小波分解系数进行近似的高通滤波处理，衰减其低频信息，增强高频信息，以达到消除雾霾噪声的目的，而且小波变换的空频特性在一定程度上保证了图像整体面貌[12]。

2.1　高频子带处理

在高频带，定义一个如下的变换函数，用来作为高频子带的增益倍数：

式中，i为小波分解的级数，a和b都是正实数，a决定了其整体增益的幅度，b则决定了各个分解级之间的幅度差。对每一个高频带上的小波系数进行非线性调整，调整方式为各个高频子带的图像乘以其相对应的增益倍数，即cH′i=cHi*H(i)等，得到与之相对应的高频细节图像。调整后的高频细节图像与原细节图像相比，高频信息得到增强，低频信息得以减弱，削弱了雾霾对图像的影响，对图像的细节信息也有所增强。考虑到设备的抖动等其他一系列原因的影响，高频部分也可能掺杂有部分噪声，所以高频子带的增益倍数也不宜过分增大。式（12）定义的高频带变换函数符合各级小波分解系数的频域倍频程特性，而且通过调整a和b的取值可以控制各级分解系数的增益大小，在保持图像原始面貌的同时增强局部对比度，消除雾霾信息的影响。

2.2　低频子带处理

对于低频子带cAτ，由于雾霾引起的低频信息主要体现在此区域的小波系数中，因此，采用n阶巴特沃斯高通滤波相对应的自适应滤波传递函数作为同态滤波函数，其表达式为：

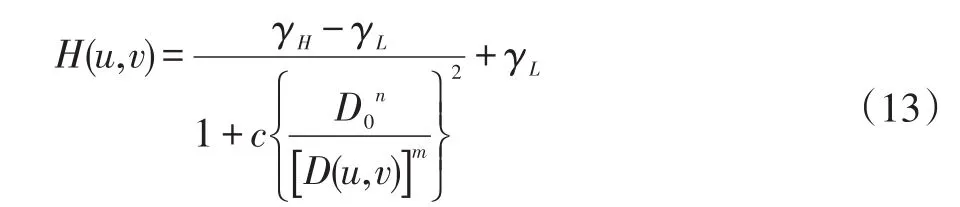
其中，常数c在γH与γL之间过渡，用来控制滤波器函数斜面的锐化，c∈[0,1]；m、n为动态算子。当γH＞1，0＜γL＜1时，图像的低频分量减弱，高频分量增加，对比度提高。用式（13）对低频近似图像cAτ进行高通滤波，进一步消除低频子带中的低频信息，考虑到同态滤波会压缩图像的动态范围，使得滤波后图像的灰度值过于集中，因此可以采用线性拉伸的方法来提高滤波后的低频子带的全局对比度，分别截断0.5%的最大灰度值和最小灰度值，确定对比度拉伸下限rmin=530和上限rmax=1220，将低频子带的数值从[530,1220]分段线性拉伸到[500,1300]，其分段线性变换函数为：

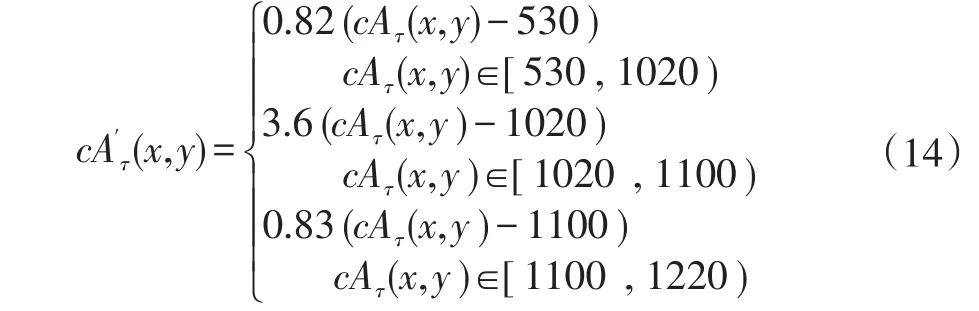
3　结果与分析

采用巴特沃斯高通滤波器、小波分析及改进的算法，基于 MATLAB软件，采用（8）式、（11）式及改进后（12）、（13）和（14）式对原图像进行增强处理，效果如图4所示。其中(a)图像为尚未处理的原始雾霾图像；(b)图像为同态滤波处理后的图像，滤波函数采用的是如式（8）的二阶巴特沃斯高通滤波函数，滤波器参数为：γH=2.0；γL=0.8；c=0.8；n=2；D0=180；(c)图像是经过小波分析处理过后的图像，小波变换采用的是‘db4’小波进行分解和重构，小波增益系数采用式（11）的变换函数,分解级数 j=3，高频增益参数为a=0.8，b=2；(d)图像为结合小波分析和同态滤波处理后的图像，图像经小波分解后，在高频的各个子带，采用式（12）的增益倍数进行增强，增益参数为在低频子带，首先经过如式（12）的n阶巴特沃斯高通滤波相对应的自适应滤波传递函数作为同态滤波函数进行滤波，滤波器滤波参数为：γH=1.8；γL=0.7；c=0.8；m=16；n=2；D0=180；由于同态滤波会压缩图像灰度值，因此可以采用如式（14）线性拉伸函数进行拉伸的方法来提高滤波后的低频子带的全局对比度。为了更准确地评价各种方法的图像去雾效果，采用文献[12]和文献[13]中的方法，以对比度、信息熵和峰值信噪比对各种方法处理前后的图像的优劣进行客观评价，相关数值如表1所示：

表1　各种算法的评价指标

图像的对比度越大，图像越清晰明亮，图像信息熵值越大，图像所含信息量就越多，而峰值信噪比决定了图像的抗干扰能力[14]。从上表中可以看出，由于雾霾的影响，原始图像的对比度和信息熵都偏低，经过同态滤波处理过后的图像，全局对比度有所增强，但信息熵却明显降低，小波变换后的图像对比度、信息熵都优于原始图像，但整体效果并不明显，结合了小波分析和同态滤波后的图像在对比度和峰值信噪比上具有显著优势，从实际图片上也可以看出由于雾霾的原因原始图像很暗，低频噪音严重影响了图片的质量，通过同态滤波后的图像由于过滤了部分能量，使得整体图像更加偏暗，小波变换后的图像明显优于原始图像，但图像整体细节仍然不够明显，细节部分仍然不够明显，结合小波分析和同态滤波后的图像很好地解决了这一问题。

4　结语

同态滤波作为经典的滤波方式，能够有效地去除雾霾图像的低频噪声，但是它对低频信号的抑制不可避免的过滤掉了图像的大部分能量，造成一定程度上的失真，在低频域尤为明显。小波分析可以将图像分为不同的频域子带，对有用的信息进行增强，也具有一定地去除雾霾信息的能力。与单一同态滤波和小波分析相比，改进后的算法结合了小波分析和同态滤波的优点，能够在有效去雾的同时保留图像的整体面貌，提高图像的整体对比度。

参考文献：

[1]王万国，王滨海，等.基于直方图规定化的图像去雾算法[J].计算机技术与发展，2009，24（9）:241-245.

[2]禹晶，徐东兵，等.图像去雾技术研究进展[J].中国图像图形学报，2011，16（9）:1561-1576.

[3]肖斌，毕秀丽，等.一种基于高斯函数的直方图规定化算法[J].铁道学报，2006，28（4）:119-121.

[4]刘春香，李洪柞.实时图像增强算法研究[J].中国光学与应用光学，2009,5（2）:390-401.

[5]马云飞，何文章.基于小波变换的雾天图像增强方法[J].计算机应用与软件，2011，28（4）:71-72.

[6]王质春，俞文燕，等.单幅雾霾天气交通监控图像去雾处理技术[J].交通运输研究，2016，7（2）:46-52.

[7]章步云，周书民，等.非稳信号的快速傅里叶变换与小波分析的比较[J].通信技术，2002（7）:1-2.

[8]张新明，沈兰荪.基于小波的同态滤波器用于图像对比度增强[J].电子学报，2001，29（4）:1-4.

[9]谢凤英，赵丹培，等.数字图像处理及应用[M].北京：电子工业出版社，2016：72-75.

[10]孙慧贤，罗飞路，等.基于小波变换和同态滤波的内窥图像增强算法[J].探测与控制学报，2008，30（5）:68-72.

[11]I.M.Johnstone，B.W.Siliverman.Wavelet Threshold Estimators for Data with Correlated Noise[J].Journal of the Royal Statistical Society,Series，1997，59:319-351.

[12]赵晓雷.基于小波变换和均值滤波的图像去噪研究[J].信息技术，2017，3（2）:69-75.

[13]周小军，谭薇，等.一种红外图像对比度增强新方法[J].无线电工程，2015，45（2）:26-29.

[14]杜喆，祁帅涛，等.基于平稳小波的电气设备红外图像对比度增强方法[J].黑龙江电力，2015,37（4）:321-325.