基于模型参考自适应方法的随动系统参数辨识

占昌恒，潘　军，王　歌，宋　鹏，韦祖拔

(西北机电工程研究所，陕西 咸阳　712099)

随动系统是一种典型的伺服系统，一般由电机、驱动器、控制器和传感器等部分组成。火炮在运转过程中，高低系统、方位系统转动惯量都会发生变化，从而引起折算到随动系统电机轴上的转动惯量发生变化，若不根据系统转动惯量参数变化调整随动控制参数，会影响随动系统控制性能，导致随动系统的控制效果变差[1]，严重时会破坏系统稳定性，导致无法完成调炮任务。为了使随动系统能够达到更好的控制效果，需要根据转动惯量的变化实时调整控制器的PI参数[2]。转动惯量值辨识的准确性和快速性直接关系到随动系统控制效果的好坏[3]。为了使随动系统得到更好的控制效果，需要对相关参数进行实时辨识[4]。参数辨识的目的是及时辨识随动系统状态参数的变化，观测随动系统的实时运行状态，并根据随动系统转动惯量的辨识值及时调整控制器的控制参数，保证随动系统处于最优的工作状态。目前常用的参数辨识方法有最小二乘法、模型参考自适应法、状态观测器法和智能算法等。模型参考自适应方法具有算法简单、便于在数字控制器中使用的优点，被广泛使用于系统辨识中。笔者采用模型参考自适应方法实现了转动惯量参数的在线辨识，通过推导永磁同步电机在稳态条件下的数学模型，将电机的机械转速、电磁转矩和定子电流等可观测量作为输入量，实时辨识出折算到电机轴上的转动惯量。

1　模型参考自适应方法原理

模型参考自适应控制(Model Reference Adaptive Control, MRAC)是从20世纪50年代后期发展起来的一种新型辨识方法，属于自适应控制系统的一种类型。从结构上MRAC可以分为参考模型、可调模型和自适应规律3个部分[5-6〗。MRAC辨识的思想是将不含未知参数的实际系统视作参考模型，将含有待辨识参数的系统视作可调模型，参考模型和可调模型的输出量的物理意义相同，通过合适的自适应规律，使两个模型的输出量之差不断缩小，直到满足辨识精度的要求。从而实现对未知参数的辨识。通常MRAC的基本结构如图1所示。图中u为控制器的输入，yk，yp分别为参考模型和可调模型的状态变量。

对模型参考自适应进行简要推导，假设MRAC中参考模型的状态方程为

(1)

式中：xk为参考模型的状态变量，可以是离散的也可以是连续的；u为模型的输入变量，通常x(0)是已知的；Ak和Bk为系统的参数矩阵，若参数矩阵都是完全可控和完全可观，通过李雅普诺夫稳定性理论和波波夫超稳定理论分析可知，参考模型是稳定的。

假设MRAC中可调模型的状态方程为

(2)

式中，Ap(ε,t)，Bp(ε,t)一般是未知的，并且是时变的，设Ap(0)=A(0),Bp(0)=B(0)，xp为可调模型的状态变量，定义可调状态变量xp的初值为x0，定义误差：

ε=xk-xp

(3)

MRAC通过不断调节可调系数矩阵Ap(ε,t)，Bp(ε,t)，使得系统稳定的条件下，当时间趋于无穷时，参考模型和可调模型的输出误差ε无限趋近于0。

根据输出误差的定义，将式(3)进行求导，可得：

(4)

将式(1)、(2)代入式(4)，可得：

(5)

从以上分析可以得到在一般情况下的模型参考自适应律为：

Ap(ε,t)=F(ε,τ,t)+A(0)

(6)

Bp(ε,t)=G(ε,τ,t)+B(0)

(7)

式中：F(ε,τ,t)为状态反馈控制器；G(ε,τ,t)为前馈控制器。

设状态反馈控制器和前馈控制器满足以下条件：

(8)

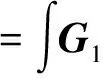
(9)

对于模型参考自适应控制能否实现优良的自适应控制系统，其中一个关键的问题就是如何确定自适应规律。自适应规律设计方法通常有3种：以局部参数最优化理论为基础的设计方法，以李雅普诺夫函数为基础的设计方法和以超稳定与正性动态系统理论为基础的设计方法。笔者采用的是波波夫超稳定性理论为基础的设计方法。

使用波波夫超稳定性理论设计模型自适应规律，可利用函数判断系统的全局稳定性和局部渐进稳定性，不需要求解系统的微分方程，能够简单直接而又准确的得到自适应规律。

采用波波夫超稳定性理论设计模型参考自适应系统应遵循以下步骤：

1)将需要设计的系统模型进行等价变换，变换的目标是：前向通道变换为线性环节，反馈通道变换为非线性时变环节或者非时变环节。

2)使得进行等价变换后的反馈环节仍然能够满足波波夫条件，通过公式推导或多次试验得到合适的自适应规律。

3)根据波波夫超稳定性理论得到前向线性环节等价变换后的系统应满足的条件(前向通道的传递函数矩阵G(s)为正实矩阵)。

4)将前面进行的等价变换系统进行还原，完成模型参考自适应规律的设计。

2　永磁同步电机辨识模型建立

永磁同步电机的机械运动方程为：

(10)

式中：Te是电磁转矩；TL是永磁同步电机的负载转矩；ωm为转子机械角速度；J为转动惯量；Bm为运动阻尼系数。

在仿真过程中，将Bm取为0，式(10)可以简化为

(11)

将式(11)进行离散化和简化处理后可得：

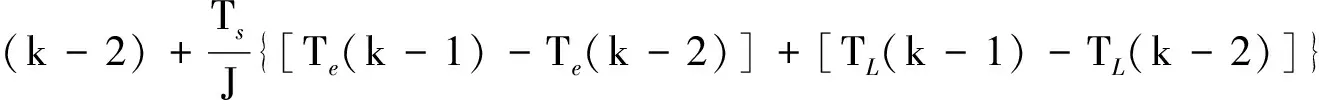
(12)

由于采样时间Ts很小，在高性能的永磁同步电机控制系统中，可以认为负载转矩在一个采样周期内的变化几乎为0。所以式(12)可简化为：

ω(k)=2ω(k-1)-ω(k-2)+bΔTe(k-1)

(13)

式中：b=Ts/J；ΔTe(k-1)=Te(k-1)-Te(k-2),以式(13)作为参考模型，参考模型的输出为永磁同步电机实际转速ω(k)。

(14)

则参考模型与可调模型的输出误差为：

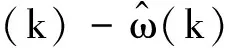
(15)

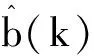
(16)

自适应增益β为模型参考自适应算法中的可变参数，通过调节自适应增益β的值来改变算法的辨识速度和辨识精度[8]。

3　仿真与分析

在MATLAB/Simulink中搭建仿真模型，采用id= 0的矢量控制，辨识模型如图2所示。

图2中，选用的交流永磁同步电机模型的转动惯量为0.000 36 kg·m2。

以式(13)为参考模型，式(14)为可调模型，式(16)为自适应规律，在MATLAB/Simulink中搭建模型，搭建的转动惯量辨识子模块如图3所示。

在仿真时，系统采用定步长仿真，步长设为1 μs，辨识模块的采样时间设为100 μs，辨识模块的输入信号为电机的机械转速和电磁转矩，通过调节β的值来获得转动惯量的辨识结果。

某火炮从低角往高角运动，或在射击过程中，高低系统和方位系统转动惯量都会发生变化。针对不同状态下折算到电机轴上的转动惯量，需要对其进行在线辨识。在仿真模型中通过手动改变折算到电机轴上的转动惯量，来模拟实际过程中的转动惯量变化，验证辨识算法的可行性和有效性。为了验证模型参考自适应辨识方法在转动惯量发生变化时的有效性，针对折算到电机轴上的转动惯量变为原来的1、3、5、10倍的情况进行了仿真试验。设置转动惯量值J=0.000 36 kg·m2，β选为3 000，通过在线辨识算法得到折算到电机轴上的转动惯量的辨识结果，如图4所示。从图中可以看出，在系统稳定时转动惯量的辨识值稳定在0.000 36 kg·m2附近。

当折算到电机轴上的转动惯量变为原来的3、5、10倍，设置β选为3 000，通过在线辨识算法得到折算到电机轴上的转动惯量的辨识结果如图5～7所示。从图5能够可以看到，当系统稳定时转动惯量的辨识值稳定在0.001 08 kg·m2附近，图6的转动惯量在系统稳定时的辨识值稳定在0 .001 8 kg·m2附近，图7的转动惯量在系统稳定时的辨识值稳定在0.003 6 kg·m2附近。

通过观察比较图4～7的辨识结果可知，模型参考自适应方法能够在折算到电机轴上的转动惯量发生变化时实现对转动惯量的辨识，在系统稳定时，转动惯量的辨识结果稳定在目标值附近。

4　结束语

为了改善随动系统的控制效果，需要能根据负载转动惯量的变化实时改变PI控制器的参数，而PI控制器的参数与转动惯量密切相关，因此转动惯量的辨识是PI参数整定的基础。笔者介绍了一种模型参考自适应方法来实现对折算到永磁同步电机轴端的转动惯量在线辨识，在MATLAB/Simulink环境下建立了模型参考自适应辨识转动惯量的模型，通过手动更改转动惯量的值来模拟实际系统中转动惯量的变化情况。从仿真结果中可知，当折算到电机轴端的转动惯量发生变化时，该辨识方法能辨识出系统当前时刻折算到电机轴上的转动惯量的值，且辨识的稳定值与设定值相接近，说明该方法具有一定的工程应用价值。

参考文献(References)

[1] 靳学谦．永磁同步伺服系统惯量辨识及参数自整定策略研究[D]．哈尔滨：哈尔滨工业大学，2011．

JIN Xueqian. Study on inertia identification and parameter self-tuning method for PMSM servo system [D]. Harbin:

Harbin Institute of Technology, 2011. (in Chinese)

[2] 张扬. PMSM伺服系统控制器参数自整定及优化[D]. 哈尔滨：哈尔滨工业大学，2009.

ZHANG Yang.Parameter self-tuning and optimum for PMSM servo system[D].Harbin:Harbin Institute of Technology, 2009. (in Chinese)

[3] 梁骄雁．永磁同步电机转动惯量辨识的研究[D]．南京：南京航空航天大学，2011．

LIANG Jiaoyan. Research on inertia identification of permanent magnet synchronous motor[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2011. (in Chinese)

[4] 王佳子．交流电动机自适应控制技术的发展现状及应用[J]．防爆电机，2008,43(6):37-40.

WANG Jiazi. Development state and application of adaptive control technology on AC motor[J]. Explosion-proof Electric Machine，2008:43(6)：37-40. (in Chinese)

[5] 陈澄.模型参考自适应辨识方法在贴片机运动控制系统中的应用研究[D].苏州：苏州大学，2013.

CHEN Cheng. Application of the identification method based on model reference adaptive system in motion control system of the placement machine[D]. Suzhou: Soochow University, 2013. (in Chinese)

[6] 杨东.模型参考算法在快速倾斜镜中的应用研究[D].北京：中国科学院大学，2013.

YANG Dong. The application of model reference algorithm in fast-inclined mirror [D]. Beijing: University of Chinese Academy of Sciences, 2013. (in Chinese)

[7] 庞中华，崔红．系统辨识与自适应控制 MATALB 仿真[M]．北京：北京航空航天大学出版社，2009．

PANG Zhonghua，CUI Hong. System identification and adaptive control MATALB simulation[M]. Beijing: Beihang University Press, 2009.(in Chinese)

[8] 桑妤.永磁同步电机转动惯量辨识算法研究[D].武汉：华中科技大学，2013.

SANG Yu. Research on inertia identification algorithm of permanent magnet synchronous motor[D]. Wuhan: Huazhong University of Science and Technology, 2013. (in Chinese)