基于生物能量学原理构建异育银鲫生长、饲料需求和污染排放模型
刘晓娟 郭 勋 王春芳 李大鹏 Dominique Bureau
(1. 华中农业大学水产学院淡水水产健康养殖湖北省协同创新中心, 池塘健康养殖湖北省工程实验室, 武汉 430070;
2. Fish Nutrition Research Laboratory, Department of Animal Bioscience,University of Guelph, ON, Canada N1G 2W1)
养殖成本和养殖产量是水产养殖从业者关注的重点。然而, 近年来, 生产成本的增加, 市场竞争导致的利润空间挤压, 以及国家、相关管理机构、甚至消费者, 对水产养殖可持续发展的要求, 让水产养殖行业面临巨大挑战[1]。养殖过程中很小的改动都将显著影响水产养殖业效益。预测养殖鱼类对饲料的需求量主要依赖于已发表的文章、以往的养殖经验以及观察饲料投喂过程中鱼类的行为。但在生产实践中, 养殖品种的投喂管理和饲料需求还是以以往的经验为主[2]。盲目的使用机械化工具(如自动投饵机), 不仅会导致饲料不可避免的浪费, 而且还增加了饲料需求量的估算难度[3]。饲料投喂过多会导致成本增加和养殖水域的污染, 投喂不足则容易导致养殖品种生长缓慢, 造成养殖效益的降低[4]。由于养殖鱼类的外部环境、遗传因素和饲料的营养质量的不同, 鱼类对饲料的需求也会产生较大的差异[3]。因此, 建立合理的鱼类能量需求模型并运用此模型来预测鱼类生长、饲料需求以及污染物排放, 可在实际养殖中为其差异化上市、节约饲料成本、减少饲料浪费以及养殖场的污染评价提供有效的预测工具。
在水产动物养殖过程中, 已有许多研究者在生物能量和营养代谢的基础上建立了一些简单的营养模型[5—13]。这些模型已经越来越多地被用到了实践养殖中, 成为预测鱼类和虾类生长、饲料需求以及废物排放的重要工具, 对水产养殖业的可持续发展具有重大意义。然而, 它们大多数忽略了鱼类在不同的生长阶段会有生长差异这一特征, 因此许多模型只适用于鱼类生长过程的某一阶段[14]。另外, 这些模型主要是根据以往经验而得出的, 其适用范围较窄[15]。因此, 需要进一步研究摄食、环境以及内源性因素对不同生长阶段鱼类营养的利用和吸收的影响, 构建更加实用的模型。
异育银鲫(Carassius auratas gibelio) 是利用天然雌核发育的方正银鲫为母本, 以兴国红鲤为父本,经人工授精繁育的子代, 生长速度比普通鲫鱼快2—3倍, 是我国鲫鱼养殖中的主要品种[16]。近年来,虽然有一些学者开始着手有关异育银鲫能量收支方面的研究, 并建立了异育银鲫的能量收支方程[17]:100C=12.32F+3.32U+63.74R+20.72G, 式中C为摄食能, F为粪便能, U为排泄能, R为代谢能, G为生长能。但到目前为止, 有关异育银鲫的复合型营养模型的研究还未有报道。本研究主要探讨不同环境下异育银鲫的能量需求, 对不同生长阶段的异育银鲫的生长规律进行研究, 并在生物能量学的基础上构建异育银鲫生长、营养需求以及污染排放(固体废物和溶解态氮、磷废物)模型, 为实际养殖中提高异育银鲫养殖质量、降低养殖污染提供一定的理论基础。本研究主要包括以下3个方面: (1) 搜集异育银鲫生长数据, 对异育银鲫生长周期进行分段,通过连续采样试验, 对鲫鱼不同生长阶段生长模型进行调整; (2)搜集异育银鲫鱼体生化成分、耗氧率、排氨率以及生长能、代谢能、排泄能等基本参数, 确定不同生长阶段异育银鲫消化能需求, 构建不同生长阶段异育银鲫饲料需求模型; (3)根据异育银鲫不同生长阶段饲料营养需求, 通过营养物质平衡法构建异育银鲫污染排放模型。
1 材料与方法
1.1 不同生长模型的比较
本研究选用了特定增长率(SGR)、日增长率(DGC)、日均增重(ADG)和热积温系数(TGC)这几种生长模型, 其计算公式如下:

式中, FBW和IBW分别为鱼体的终末体重和初始体重, d为养殖天数, t为养殖水温, (1-b)为TGC模型体重指数。
根据上述公式, 异育银鲫的生长预测公式如下:

为了明确鱼类的生长速度和其生长阶段之间的关系, 本研究查阅并收集文献中鱼类的初末体重、养殖时间、水温等数据, 根据上述公式分别计算SGR、DGC、ADG、TGC等值, 拟合其生长曲线,再将鲫鱼的预测体重和实际养殖中的观测值进行比较, 选择最适生长模型。在积温系数TGC的计算中, 其指数(1-b)首先按照1/3计算, 随后进行调整,采用模型预测值和养殖观测值的最小残差平方和法校正[18], 直到 RSS数值最小, RSS的计算采用迭代法, 工具采用Excel 2013。由于b>0[19], 故当RSS最小时, 1-b<1。残差平方和公式如下:
其中yj代表生长过程中的观测值, Yj代表预测值。
1.2 生化成分分析
异育银鲫的生化成分数据来自于46篇文献中的216个观测值, 文献出版时间为1987年到2017年,异育银鲫的体重为0.25—302.7 g。在选择文献中,生化成分的测定方法采用AOAC[20]的标准测定方法。异育银鲫的生化成分分析采用异育银鲫体重(BW)和其水分(BWat)、蛋白(BP)、脂肪(BL)、灰分(BA)和能值(GE)含量之间的回归分析描述。
1.3 各能量的估算
鱼类基础代谢(HeE)也称为静止代谢。鱼类进行有氧代谢所需要的能量与消耗的氧气成正比, 因此, 大多数研究都采用测定呼吸实验中耗氧量来估算静止代谢。本文异育银鲫耗氧量的数据均来自文献, 氧热系数采用13.6 J/mg。由于HeE和BW二者关系为HeE=A×WB, 一般鱼类的指数B为0.8, 故HeE采用以下公式计算[3]:

式中, T为水温, a, b为常数, BW为体重。
尿液和鳃的能量损失(UE+ZE)主要是通过代谢氮废物排出的。鱼类在正常情况下每消耗1 g氮相当于损失了24.9 J的能量, 因而可以通过测定鱼类的排氨率来计算UE+ZE, 本研究异育银鲫排氨率数据均来自文献。HiE主要为摄食中产生的能量,可用总摄食能(IE)与粪便能(FE)、储积能(RE)、UE+ZE、HeE之差来估算, 公式如下:

鱼类在不同的生长阶段对饲料的需求量由消化能(DE)决定[2], 通过计算RE、HeE、HiE以及UE+ZE的和, 可以估算鲫鱼DE需求量, 进而获得异育银鲫在养殖的某个时期对饲料的需求量:

1.4 废物排放量的估计
在养殖过程中, 总污染物(TW)主要包括固态污染物(SW)以及已经溶解在养殖水体中的溶解态污染物(DW), 养殖中的污染物排放预测模型如下:
TSW=DM×(1-ADC of DM)
式中TSW为总的固态废物的含量, ADC为表观消化率, DM为干物质, 同样的方程式也可运用于估算N、P污染物的排放上。
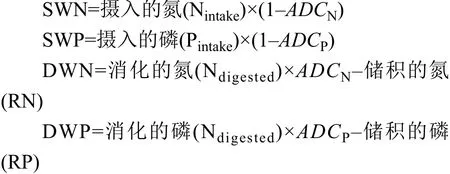
在上述公式中SWN和SWP分别代表固态氮污染物和固态磷污染物, DWN和DWP分别为溶解态氮污染物和溶解态磷污染物。
1.5 验证试验
验证异育银鲫生长和饲料需求模型的数据主要来自公安崇湖渔场。共有9个池塘, 每个月采样1次, 每个池塘采20条鱼样以及100 g饲料, 记录鱼体质量、水温等数据。对采集的鱼样和饲料样品进行化学成分分析。调整后的异育银鲫生长模型用预测体重与实际体重比较来验证。饲料需求模型使用实际和预测的饲料系数(FCR)来验证。
1.6 摄食率和废物排出量估算
本研究根据验证试验中异育银鲫在不同生长阶段中的饲料营养成分估计摄食率和废物排出量。饲料DE可通过饲料中粗蛋白消化率(ADCCP)、粗脂肪消化率(ADCCL)以及碳水化合物消化率(ADCCHO)来估算。公式如下:

TSW以及N、P污染物分别由干物质、粗蛋白(ADC 81%)、磷(ADC 68%)的表观消化率估算。可消化干物质含量为可消化粗蛋白、脂肪(ADC 90%),碳水化合物(ADC 60%)和灰分(ADC 50%)的总和。
2 结果
2.1 生长阶段的划分
为了预测异育银鲫的生长趋势, 本研究共收集了98篇文献中的420个异育银鲫生长数据(异育银鲫体重范围0.2—550 g), 并根据上述公式分别计算SGR、DGC、TGC、ADG的值。结果发现, 在用TGC模型计算其生长速率时, 异育银鲫在其生长周期中的生长性能具有一定的规律(图1), 分段性分析不同体重异育银鲫的积温系数, 发现异育银鲫在其生长周期中含有2个异速生长点(两条线段之间的交点), 根据该点的位置, 可将异育银鲫的生长周期划分为3个阶段(图2): 0.25—13.1 g (第一阶段)、13.1—172.8 g (第二阶段)、>172.8 g (第三阶段)。图1和图2中各种参数(斜率、系数、异速生长点)均使用工具Excel 2013确定。
2.2 生长模型的选择
异育银鲫在不同生长阶段的各个子模型的最适体重指数(1-b)存在显著差异。在第一生长期, 异速生长模型SGR、DGC、TGC 和调整后的TGC模型(2.4—35.0)的残差平方和明显低于ADG模型(316.2)(表1、图3A), 因而能比线性模型更好的预测异育银鲫的生长情况。在第二生长期, 只有指数调整为0.27的TGC模型(RSS为39)预测效果明显比其他任何模型更好(RSS为282—18122)(表1、图3B)。在第三生长期, ADG和指数调整为1的TGC模型(相当于是一个线性函数)的预测效果相同(RSS都为508), 但明显优于SGR (RSS= 87711)、DGC(RSS=40700)和TGC (RSS=40700)模型(表1、图3C)。因此, 只有校正后的TGC模型能够最好的预测整个生长周期的生长速率。
2.3 鱼体生化成分

图1 不同生长阶段异育银鲫积温系数Fig. 1 Thermal-unit growth coefficient (TGC) of the gibel carp on different growth stages

图2 分段性分析不同体重鲫鱼的积温系数Fig. 2 Piecewise linear analysis of the thermal-unit growth coefficient (TGC) as a function of body weight (BW)
异育银鲫在体重小于2 g时, 其相对体成分随着体重的变化具有显著差异, 在体重大于2 g时, 体重与体化学成分如BWat (-0.03)、BP (0.0008)、BL(0.0053)和BA (0.0092)之间的回归方程斜率都接近于0 (图4)。因此, 简单的等速线性方程可以有效估计异育银鲫BP (图5a)、BL (图5b)、BA (图5c)和GE (图5d)含量。当分别用对数方程和等速线性方程来预测不同体重的异育银鲫体化学成分时发现,除BP的预测效果相同外, 在BL、BA和GE的预测中, 等速线性方程都优于对数方程(方程1—4, 表2)。此外, 在异育银鲫体重为1—180 g的时候(方程5), 鱼体内磷含量同样也随着鱼体体重呈等速增加。
2.4 各种能量的估计
异育银鲫生化成分组成、HeE、HiE、UE+ZE以及DE需求量的计算公式见表3。由方程6可看出, 异育银鲫HeE除与体重直接相关外, 还与水温具有一定的关系。当水温在一定范围内时, 异育银鲫的HeE随水温的增加而增加。另外, 研究还发现,异育银鲫摄食活动产生的HiE与RE和HeE之间呈正相关关系(图6, 方程7); UE +ZE则与IE和DE密切相关, 为3.8% 的RE+HeE+HiE (图6b, 方程8)。
2.5 模型验证, 摄食率和污染物排放
验证该模型的数据主要来自公安崇湖渔场(中国, 荆州)。模型的验证使用异育银鲫体重与饲料系数(FCR)的实际观测值和模型预测值之间的相关关系来比较, 研究发现鱼体湿重、体重增量和FCR在实际值和预测值之间显著相关(R2分别为0.998和0.857,P<0.001)(图7)。
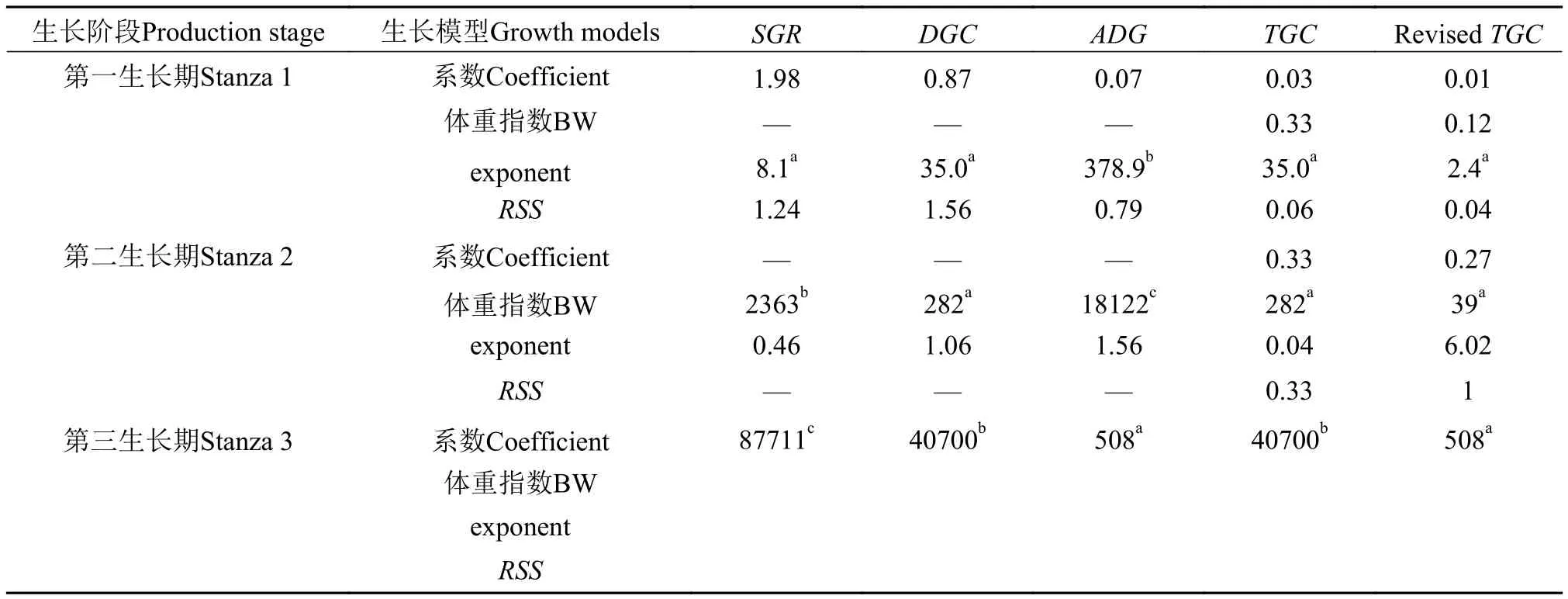
表1 异育银鲫在3个不同生长阶段SGR、DGR、ADG、TGC以及调整后的TGC体重系数和残差平方和Tab. 1 The regression coefficients, body weight (BW) exponents and residual sum squares (RSS) of specific growth rate (SGR), daily growth coefficient (DGC), linear, thermal-unit growth coefficient (TGC) and revised TGC models for the nursery, pre-grow out and grow out stages of gibel carp

图3 不同生长模型的比较-分别用SGR、DGC、ADG、TGC和Rev. TGC这几种生长模型来描述异育银鲫的生长Fig. 3 Comparison of different growth models of SGR, DGC,ADG, TGC and Rev. TGC model describes the growth of gibel carp
从表4可看出, 异育银鲫摄食率随体重的增加而下降, 在体重为1 g时每条鲫鱼每天摄食率约为4%, 而当其体重为500 g时, 摄食率降到了0.8%。异育银鲫总固体废物排放量和总可溶性含氮废物预测排放量见表5, 经估算, 对于体重为0.25—506 g的异育银鲫, 每消耗1 kg饲料以及每生产1 kg异育银鲫, 所排放的总固态废物分别为282和419 kg。
3 讨论
以往的鱼类生物能量学模型大多是建立在天然饵料基础上的[21,22]。现如今, 随着饲料加工行业的不断发展, 超过80%的异育银鲫养殖都依靠商业配合饲料。因此, 在人工饲料投喂的基础上构建饲料需求模型, 对于提升水产养殖中的经济效益, 降低养殖中的废物排放有重大意义。近年来, 已有一些研究者开始尝试在生物能量学的基础上构建一些饲料需求模型, Trung等[12]在2011年首次利用营养模型, 对集约化养殖条件下尼罗罗非鱼(Tilapia nilotica)的饲料需求进行预测, 随后Chowdhury等[3]构建了罗非鱼的复合性营养模型, 有效的评估了商业养殖中罗非鱼饲料需求以及废物排放量。本文基于生物能量学方法建立了异育银鲫生长、饲料需求以及污染排放模型。采用TGC模型, 参照Dumas等[19]方法, 将异育银鲫的生长周期分为了3个阶段: 第一生长期(<13.1 g)、第二生长期(13.1—172.8 g)和第三生长期(>172.8 g)。
3.1 生长模型

图4 异育银鲫鱼体化学组成及能量与体重的关系Fig. 4 Whole body chemical composition and gross energy of gibel carp in relation to body weight

图5 异育银鲫体重和鱼体蛋白质(4a和4e)、脂肪 (4b和4f)、灰分 (4c和4g)和生长能 (4d和4h)之间的等距和对数回归分析Fig. 5 Isometric and allometric relationship between whole body mass and body protein (4a and 4e), lipid (4b and 4f), ash (4c and 4g) and gross energy (4d and 4h)
许多鱼类在不同生长阶段存在异速生长点[23,24],需要找出异速生长点并对生长模型进行调整。Dumas等[19]根据虹鳟(Oncorhynchus mykiss)在不同阶段生长速率的不同, 将虹鳟生长周期划分为3个阶段。这表明用单个系数或体重指数的模型来描述鱼类的整个生命周期的生长特征并不是非常适用的。同时Dumas的研究表明, 只有当鱼体重量在20—500 g之间, 原有生长指数为1/3的TGC模型才具有较好的预测效果。Chowdhury等[3]对罗非鱼(Oreochromis spp.)的生长模型研究表明, 在第二生长期和第三生长期, 采用迭代法不断调整TGC模型的系数和指数后, TGC模型比单一的指数模型更加精确。生长指数为1/3的TGC模型只适用于体重小于30 g的罗非鱼, 随着鱼体重量的增加, 其生长指数(1-b)的数值也会呈现逐渐增加的趋势, 随着鱼体重量的无限增加, 该指数(1-b)的理论数值会趋近1。本文对异育银鲫的研究结果和罗非鱼的研究结果一致, 但具体系数值和罗非鱼的研究存在较大的差异, 这可能是由于不同鱼类的生长潜力不同而导致的。本文对异育银鲫的研究发现, 在第一生长期,各模型的预测值和观测值之间的残差平方和差别不大, 但是随着异育银鲫体重的增加, 不同模型的预测值和实际观测值之间的残差平方和差异明显,相似的结果也出现在罗非鱼[3]、虹鳟[19]和草鱼(Ctenopharyngodon idellus)[25]的研究中。针对以上结论, 在异育银鲫的生长预测模型中, 采用迭代法调整生长系数和生长指数后的TGC模型能够比其他模型(ADG、DGC、SGR和TGC)有更好的预测效果(预测值和观测值之间的残差平方和最小)。
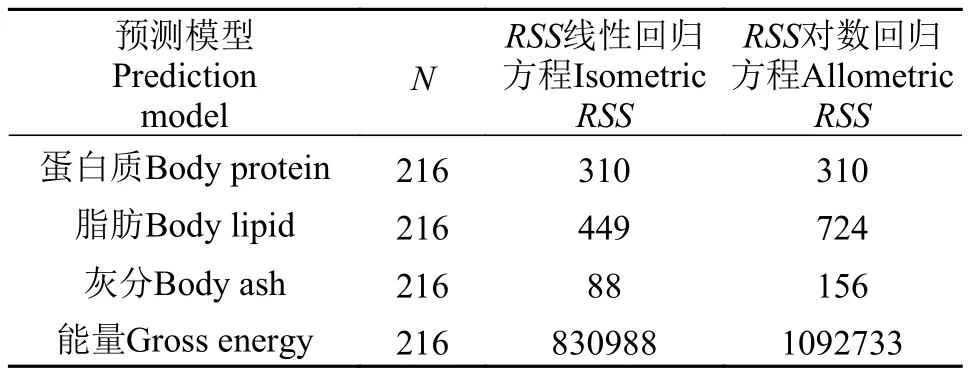
表2 线性方程和对数方程(体重与BP、BL、BA和GE)预测值与实际观测值的残差平方和(RSS)Tab. 2 Residual sum squares (RSS) of the isometric and allometric regression analysis of body weight with body protein,lipid, ash and gross energy as predictors
3.2 异育银鲫饲料需求模型
鱼类营养需求模型需要准确的反映鱼类对各营养成分的需求范围以及蛋白质、脂肪、矿物质和水等对鱼类体重增加做出的贡献。异速生长方程(Y=a×BWb)已被很多学者用来描述鱼体体重和其化学成分之间的关系[6,7,10,26]。为了预测异育银鲫鱼体化学成分, 本研究对异速生长和等速生长模型都进行了实验验证。研究结果表明, 在水体温度、鱼类大小、饲料成分和投喂水平具有差异的情况下, 简单的等速线性模型仍然可以有效的在实践中描述鱼体质量和鱼体生化成分之间关系。研究结果还表明, 异育银鲫体内脂质增加是等速的, 这与罗非鱼[3]和草鱼[25]的研究结果一致, 但与虹鳟[19]中脂质的异速生长不同。

表3 异育银鲫生化成分组成、基础代谢、增值热、排泄代谢能以及消化能需求量方程Tab. 3 The equations for the estimation of body chemical composition, basal metabolism, heat requirement of feeding, urinary-branchial excretion and digestible energy requirement

图6 热增能(HiE)、排泄能(UE+ZE)与其他能量之间的关系Fig. 6 The relationship between heat increment of feeding (HiE), urine and gills energy (UE+ZE) and other energy

图7 异育银鲫日均增长率的观测值和预测值(a1)和体重的观测值和预测值关系图(a2); 饲料转化率的观测值和预测值(b1)以及它们之间关系图(b2)Fig. 7 Observed and predicted average daily gain (g) of gibel carp (a1) and the relation between observed and predicted body weight (g)(a2); Observed and predicted feed conversion ratio of gibel carp (b1) and the relation between them (b2)

表4 在水温为26℃的条件下体重为1—500 g异育银鲫日均饲料需求量(%体重)Tab. 4 General daily feeding rates (%BW) of gibel carp reared at 26℃ growing from 1—500 g
3.3 能量收支和废物排放模型
动物需要不断供应能量才能维持机体的各项生命活动。HeE是动物维持生命器官所有活动最基础的能量, 鱼类HeE和鱼类体重以及水温有直接关系[27]。本研究异育银鲫的各种能量代谢数据均来自于已发表的文献。通过计算鱼体RE、HeE、HiE以及UE+ZE, 可以估算出异育银鲫的DE, 从而确定异育银鲫饲料需求量。结合表4、表5估算,对于体重为0.25—506 g的异育银鲫, 每生产1 kg鱼,其DE需求量约为: 1.94×104kJ, 饲料需求量为1.47 kg。
有研究表明, 一些简单的指数方程如HeE=(a+bT)×BW0.8可以用来描述温度对鱼类HeE的影响[3,4,25,28]。相比RE, 拥有较小标准误差SE(±0.015)的HeE能更好的预测HiE。而如果使用RE+HeE作为因变量, 则精度可以进一步增加[SE±0.004; 图6, 方程(8)]。异育银鲫的HiE分别约为98% HeE、1.5 RE或60% (RE+HeE), 约占总DE摄入量的三分之一, 这远远大于罗非鱼、虹鳟和其他物种中观察到的值。在Kaushik等[29]的研究中虹鳟的HiE约等于60% HeE; 对于鲷鱼(Sparus aurata)和多宝鱼(Scophthalmus maximus), 它仅相当于40% HeE[30]。这种特异性差异可能是不同品种鱼类的生长潜力不同导致的。本研究中异育银鲫UE+ZE的估算结果与罗非鱼[2]、虹鳟[27]十分相似约为4% (RE+HeE+HiE)。

表5 异育银鲫固态废物和可溶性废物排放量Tab. 5 Output of solid and dissolved wastes of gibel carp
有研究发现, 基于生物能量学基础的营养模型同样可以用来估算水产养殖的营养负荷[1,31—34], 在本研究中, 每吨饲料和每吨鱼的总固体污染物排放量分别为282和419 kg, 这比罗非鱼[3]的排放量(分别为331和432 kg/1000 kg)低, 但显著高于虹鳟[35]的排放量(分别为220和250 kg/1000 kg)。这可能与鱼类品种和饲料营养成分不同有关。本模型预测的FCR在整个生产周期中其预测值(1.47)与观察值相一致(1.51), 表明该模型能够高度有效的估计饲料的需求量和利用率。
4 结论
本研究拟合的异育银鲫生长、饲料需求和污染排放模型是在收集文献资料中饲料营养组成, 鱼类生长速度和鱼体的营养生化成分组成相关数据的基础上构建的。该生物能量学模型考虑到了水温对饲料需求量、鱼类生长、代谢需求和排泄率的综合影响。这一点在构建鱼类生长和饲料需求模型中极为重要, 因为当鱼类在不可控的养殖条件下时(如在湖泊、河流或池塘的网箱养殖中), 鱼类可能会受到季节性和垂直水温变化的影响, 从而导致鱼类的各种生长、代谢指标发生较大差异, 造成模型的准确度明显下降。
在本研究中, 鱼体湿重、体重增量和FCR在实际值和预测值之间的高度相似证明该模型可以有效的估计异育银鲫在实际养殖中的饲料需求量和污染物排放量。然而, 在特定的农业生产条件下,为使结果更加精确, 还需要利用以往该养殖条件下的周年连续采样获得的数据重新调整增长模型。
参考文献:
[1]Dumas A, De Lange C F M, France J, et al. Quantitative description of body composition and rates of nutrient deposition in rainbow trout (Oncorhynchus mykiss) [J].Aquaculture, 2007a, 273(1): 165—181
[2]Cho C Y, Bureau D P. Development of bioenergetic models and the Fish-PrFEQ software to estimate production,feeding ration and waste output in aquaculture [J]. Aquatic Living Resources, 1998, 11(4): 199—210
[3]Chowdhury M A K, Siddiqui S, Hua K, et al. Bioenergetics-based factorial model to determine feed requirement and waste output of tilapia produced under commercial conditions [J]. Aquaculture, 2013, 410—411(2):138—147
[4]Bureau D P, Hua K. Models of Nutrient Utilization by Fish and Potential Applications for Fish Culture Operations [M]. Mathematical Modeling in Animal Nutrition.CBA international, Wallingford. 2008, 442—461
[5]Bailey J, Alanärä A. A test of a feed budget model for rainbow trout, Oncorhynchus mykiss (Walbaum) [J].Aquaculture Research, 2001, 32(6): 465—469
[6]Booth M A, Allan G L, Pirozzi I. Estimation of digestible protein and energy requirements of yellowtail kingfish(Seriola lalandi) using a factorial approach [J]. Aquaculture, 2010, 307(3): 247—259
[7]Glencross B D, Bermudes M. Adapting bioenergetic factorial modelling to understand the implications of heat stress on barramundi (Lates calcarifer) growth, feed utilization and optimal protein and energy requirements-potential strategies for dealing with climate change [J]?Aquaculture Nutrition, 2012, 18(4): 411—422
[8]Hua K, de Lange C F M, Niimi A J, et al. A factorial model to predict phosphorus waste output of rainbow trout (Oncorhynchus mykiss) [J]. Aquaculture Research,2008, 39(10): 1059—1068
[9]Hua K, Birkett S, De Lange C F M, et al. Adaptation of a non-ruminant nutrient-based growth model to rainbow trout (Oncorhynchus mykiss Walbaum) [J]. The Journal of Agricultural Science, 2010, 148(1): 17—29
[10]Lupatsch I, Kissil G W, Sklan D. Defining energy and protein requirements of gilthead seabream (Sparus aurata L.) to optimize feeds and feeding regimes [J]. Israeli Journal of Aquaculture-Bamidgeh, 2003, 55(4):243—257
[11]Pirozzi I, Booth M A, Allan G L. A factorial approach to deriving dietary specifications and daily feed intake for mulloway, Argyrosomus japonicus, based on the requirements for digestible protein and energy [J]. Aquaculture,2010, 302(3): 235—242
[12]Van Trung D, Diu N T, Hao N T, et al. Development of a nutritional model to define the energy and protein requirements of tilapia, Oreochromis niloticus [J]. Aquaculture,2011, 320(1): 69—75
[13]Zhou Z G, Xie S Q, Wu L, et al. A bioenergetic model to estimate feed requirement of gibel carp, Carassius auratus gibelio [J]. Aquaculture, 2005, 248(1): 287—297
[14]Nickerson D M, Facey D E, Grossman G D. Estimating physiological thresholds with continuous two-phase regression [J]. Physiological Zoology, 1989, 62(4):866—887
[15]Bureau D P, Kaushik S J, Cho C Y. Bioenergetics. In:Halver J E, Hardy R W (Eds.), Fish Nutrition [M]. San Diego: Academic Press. 2002, 1—53
[16]Xu L, Liu B, Xie J, et al. Effects on mannose oligosaccharides on growth performance, immunity and HSP70 expression of juvenile crucian carp (Carassius auratus gibelio) [J]. Acta Hydrobiologica Sinica, 2012, 36(4):656—664 [徐磊, 刘波, 谢骏, 等. 甘露寡糖对异育银鲫生长性能, 免疫及HSP70基因表达的影响. 水生生物学报, 2012, 36(4): 656—664]
[17]Zhu X M, Xie S Q, Cui Y B. Effect of ration level on growth and energy budget of the Gibel carp, Carassius auratus gibelio [J]. Oceanologia et limnologia Sinica,2000, 5(31): 471—479 [朱晓鸣, 解绶启, 崔奕波. 摄食水平对异育银鲫生长及能量收支的影响. 海洋与湖沼,2000, 5(31): 471—479]
[18]Vittinghoff E, Glidden D V, Shiboski S C, et al. Regression methods in Biostatistics: Linear, Logistic, Survival,and Repeated Measures Models [M]. New York: Springer.2005, 340
[19]Dumas A, France J, Bureau D P. Evidence of three growth stanzas in rainbow trout (Oncorhynchus mykiss)across life stages and adaptation of the thermal-unit growth coefficient [J]. Aquaculture, 2007b, 267(1):139—146
[20]AOAC. Official Methods of Analysis[M]. AOAC International, Washington, DC. 1995, 16
[21]Yi Y. A bioenergetics growth model for Nile tilapia (Oreochromis niloticus) based on limiting nutrients and fish standing crop in fertilized ponds [J]. Aquacultural Engineering, 1998, 18(3): 157—173
[22]Yi Y. Modeling growth of Nile tilapia (Oreochromis niloticus) in a cage-cum-pond integrated culture system[J]. Aquacultural Engineering, 1999, 21(2): 113—133
[23]Parker R R, Larkin P A. A concept of growth in fishes [J].Journal of the Fisheries Research Board of Canada,2011, 16(5): 721—745
[24]Shearer K D. Factors affecting the proximate composition of cultured fishes with emphasis on salmonids [J].Aquaculture, 1994, 119(1): 63—88
[25]Luo W. Fish-PrFEQ model to determine feed requirement and waste output of grass carp under commercial conditions [D]. Wuhan: Huazhong Agricultural University. 2016 [罗伟. 运用Fish-PrFEQ程序建立草鱼投喂管理和污染排放模型. 硕士学位论文, 华中农业大学,武汉. 2016]
[26]Weatherley A H, Gill H S. The Biology of Fish Growth[M]. London: Academic Press.1987, 443
[27]Kaushik S J. Nutritional bioenergetics and estimation of waste production in non-salmonids [J]. Aquatic Living Resources, 1998, 11(4): 211—217
[28]Cho C Y. Prediction model for energy requirement of salmonid fishes [C]. 12th Symposium of Energy Metabolism of Farm Animals. 1991, (58): 446—449
[29]Kaushik S J, Doudet T, Medale F, et al. Protein and energy needs for maintenance and growth of Nile tilapia(Oreochromis niloticus) [J]. Journal of Applied Ichthyology, 1995, 11: 290—296
[30]Guinea J, Fernandez F. Effect of feeding frequency, feeding level and temperature on energy metabolism in Sparus aurata [J]. Aquaculture, 1997, 148(2): 125—142
[31]Azevedo P A, Podemski C L, Hesslein R H, et al. Estimation of waste outputs by a rainbow trout cage farm using a nutritional approach and monitoring of lake water quality[J]. Aquaculture, 2011, 311(1): 175—186
[32]Bureau D P, Gunther S J, Cho C Y. Chemical composition and preliminary theoretical estimates of waste outputs of rainbow trout reared in commercial cage culture operations in Ontario [J]. North American Journal of Aquaculture, 2003, 65(1): 33—38
[33]Cho C Y, Hynes J D, Wood K R, et al. Development of high-nutrient-dense, low-pollution diets and prediction of aquaculture wastes using biological approaches [J].Aquaculture, 1994, 124(1-4): 293—305
[34]Ogunkoya A E, Page G I, Adewolu M A, et al. Dietary incorporation of soybean meal and exogenous enzyme cocktail can affect physical characteristics of faecal material egested by rainbow trout (Oncorhynchus mykiss)[J]. Aquaculture, 2006, 254(1): 466—475
[35]Bureau D P, Hua K. Towards effective nutritional management of waste outputs in aquaculture, with particular reference to salmonid aquaculture operations [J].Aquaculture Research, 2010, 41(5): 777—792

