某履带车辆盘式制动器制动盘的瞬态热分析
米召阳, 穆洪斌, 廖桐舟, 徐 冰, 杨志勇
(1.中国北方车辆研究所,北京 100072;2.北京理工大学,北京 100081)
制动器是车辆制动的执行机构,制动器性能的优劣直接影响车辆的性能与安全.坦克用制动器分为带式制动器、鼓式制动器、盘式制动器,其中盘式制动器体积小、散热能力强、制动力矩稳定,应用越来越广泛[1].我国军用车辆发展迅速,性能越来越强,机动性越来越好,这就对坦克的制动机构提出了更高的要求,因此研究盘式制动器对提升某履带车辆的性能至关重要,本研究分析了某履带车辆盘式制动器紧急制动过程中的热分布与应力应变情况.
朱永梅[2]等作者利用ABAQUS对盘式制动器进行了热结构直接耦合分析,分析结果对制动盘材料选择、结构尺寸设计、制动工况选择、制动盘破坏预防等工作提供了可靠依据.罗继华[3]等作者采用将制动摩擦面的散热转化为逆向热流密度的方法,研究了制动过程中制动盘的温度分布及变化规律、盘内热应力分布、最大热应力发生位置.王营[4]等作者研究了制动过程的能量转换及摩擦生热机理,建立制动器热流密度分配模型,揭示了摩擦制动时摩擦片内温度分布规律,为摩擦制动器的设计提供可靠依据.马保吉[5]等作者研究了路面车辆从开始制动到停止的紧急制动全过程,建立了紧急制动过程各参数的动态模型和制动器热流密度模型,为制动器温度场分析提供了更合理的热流密度边界条件.Kiple RC[6]等作者与周志勇[7]等作者的研究证明,盘式制动器制动过程中产生的急速变化的热应力与制动盘的寿命有重要关系.日本管原繁夫[8]研究了轨道列车紧急制动时,制动盘面温度的急剧升降,将引起材料表面发生龟裂,严重影响制动盘的使用寿命.刘艳[9]等作者研究了客车制动过程中制动盘的热流密度和对流散热系数,利用ABAQUS对其进行热结构直接耦合分析,为制动盘工况的选择提供参考,从而能有效预防制动盘的破坏.
1 理论计算
某履带车辆在速度为65 km/h制动时,主要通过机械式制动盘制动,动能转化为热能,能量经两次分配耗散,一部分由履带与路面之间的摩擦消耗,另一部分由制动器吸收,使制动器元件温度升高,制动器吸收的能量在摩擦副对偶件间存在二次分配[5].制动器与制动工况的主要参数如表1所示.

表1 制动器参数
粉末冶金制动片有摩擦系数高、磨损小、稳定性好等优点,在500 ℃以上仍可保持良好的摩擦性能,且基体为金属,导热性好,不受雨雪天气等的影响,因此其在装甲车辆上得到了广泛应用[10].本研究所用盘式制动器,选择的摩擦副材料为碳素结构钢-干式铜基粉末冶金材料.制动盘为优质碳素结构钢65Mn;制动片为干式铜基粉末冶金材料,主要成分为金属,并添加石墨和铅以提高耐磨性与防止粘着.其参数如表2所示.

表2 制动盘与制动片材料物理性能参数
1.1 热流密度的计算
通常热流密度的计算有两种方法,一种是能量折算法,一种是功率折算法.这里以研究紧急制动过程中制动盘最高温度随时间的变化为主,所以径向线速度导致的热流密度差异可以忽略,因此在计算热流密度时采用能量折算法.
车辆质量为M,制动片与制动盘单面接触面积为Azd.制动过程为匀减速,在时间t内,速度由初速度va减为vb,因此制动器的热流密度[11]:
(1)
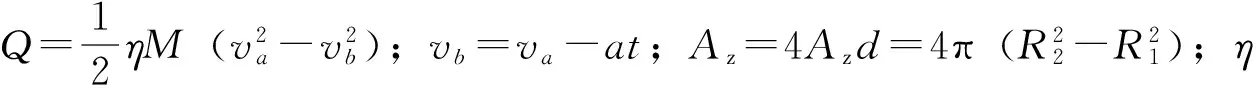
匀减速制动时,制动器的热流密度为:
(2)
由于制动盘与制动片的密度、比热容、导热系数的不同[12],所以热流量存在分配比例系数ε.
(3)
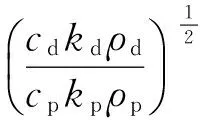
计算得到:ε=63.06%.
由计算结果可见,车辆制动时,制动盘吸收的能量大于制动片吸收的能量,这里使用的铜基粉末冶金材料型摩擦片由于其良好的导热能力,可以有效降低对偶盘的热负荷,这对于质量较大的履带装甲车辆在紧急制动时降低制动盘的热负荷是十分重要的[10].
根据式(2)、式(3)可以得到,制动盘的热流密度qd(t)和制动片的热流密度qp(t).如式(4)和式(5)所示.
(4)
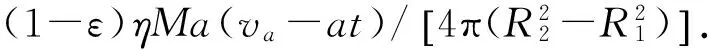
(5)
制动过程中,最大减速度aa=4.98m/s2,制动总时间ta=t1+t2.
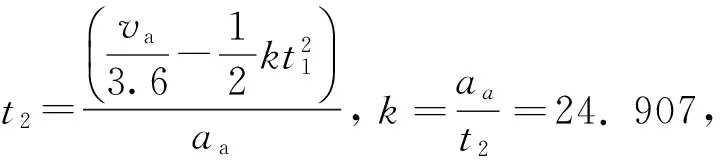
所以制动时间为:ta=t1+t2=3.724 6 s.
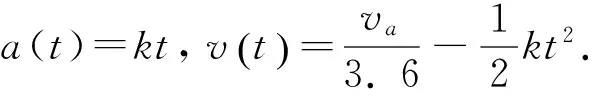
(6)
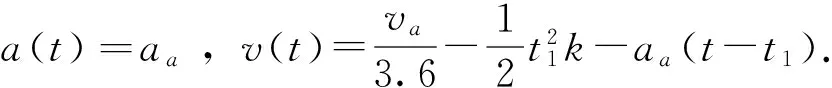
(7)
使用Matlab输出qd(t)曲线如图1所示,图中热流密度最大为7.18×106W/m2.
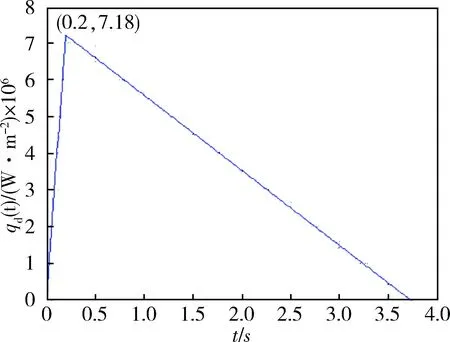
图1 制动盘热流密度曲线
由图1可知,在车辆紧急制动的初始阶段,由于制动盘转速最高、与制动片的相对摩擦速度最大,流入制动盘的热流密度急剧增大,0.2 s时达到最大值.随着时间的推移,热流密度逐渐降低,在流入的能量与流出的能量达到平衡之前,制动盘的温度持续升高.当流入的能量小于流出的能量之后,制动盘的温度开始逐渐降低,约3.7 s之后,制动盘抱死,流入制动盘的热流密度降为零,之后随着能量的不断流出,制动盘温度持续降低,直到降至环境温度.
1.2 对流换热系数的计算
制动过程中对流换热系数与材料无关,与制动盘形状和制动盘表面的空气流速有关,因此不同部位的换热系数不相同.根据传热学理论,制动盘对流换热系数为[11]:
(8)
式中:空气温度22 ℃;Pr为普朗特常数,空气Pr=0.7;λa为空气导热系数,空气λa=0.025 9 W/(m·K);L为壁面长度,L=D=0.43 m;u为空气流动速度,m/s;ν为空气的运动粘度,ν=1.509×10-5m2/s.
(1)确定制动盘表面空气流速u.
制动盘相对于空气的运动为随输出轴的转动和随整车的平动,因此制动盘表面空气流速u为转动与平动的向量合成,为方便理论研究,可假设二者垂直,则:
(9)
式中:v为平均车速,v=9.028m/s;ω为平均角速度,ω=169.5rad/s;r为平均半径,r=0.215m.
经计算得到u=37.5 m/s,制动盘与空气间的对流换热系数hc1=131.8 W/(m2·K).
(2)确定散热筋板处空气流速u.
为提高散热效率,应使散热筋板与空气的接触面积尽可能大,因此散热筋板的几何结构一般较为复杂.整体随车辆平动,可取车辆速度来近似空气流速,u=9.028 m/s.代入式(8)得到散热筋板与空气间的对流换热系数hc2为42.2 W/(m2·K).
总对流换热系数为
hc=hc1+hc2.
(10)
经计算,hc为174 W/(m2·K).
在实际换热的边界条件中,除了径向和轴向的对流换热,还有辐射换热.由于辐射换热的计算较为复杂,并且其对温升的影响很小,因此忽略辐射换热的影响.
1.3 温升的计算
为了近似得到制动盘的温升,需要做出能量去处的假设.初始时刻绝大多数的热量出现在制动盘面上[13],随后迅速被周围元件和气流冷却.制动盘最高温度为:
(11)
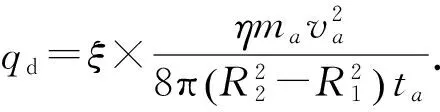
式中:Tmax为制动盘最高温度,℃;qd为制动盘平均热流密度,经计算为3.86×106W/m2;ta为制动时间,s;ρd为制动盘材料密度,kg/m3;cd为制动盘热容率,J/(kg·K);kd为制动盘热导率,W/(m·K);T0为环境温度,22 ℃.
经计算得到,Tmax=524.43℃.
作为对比,制动盘表面温升的计算可采用式(12)计算[1].
(12)
根据式(12)得到制动盘表面温度随时间的变化曲线如图2所示.
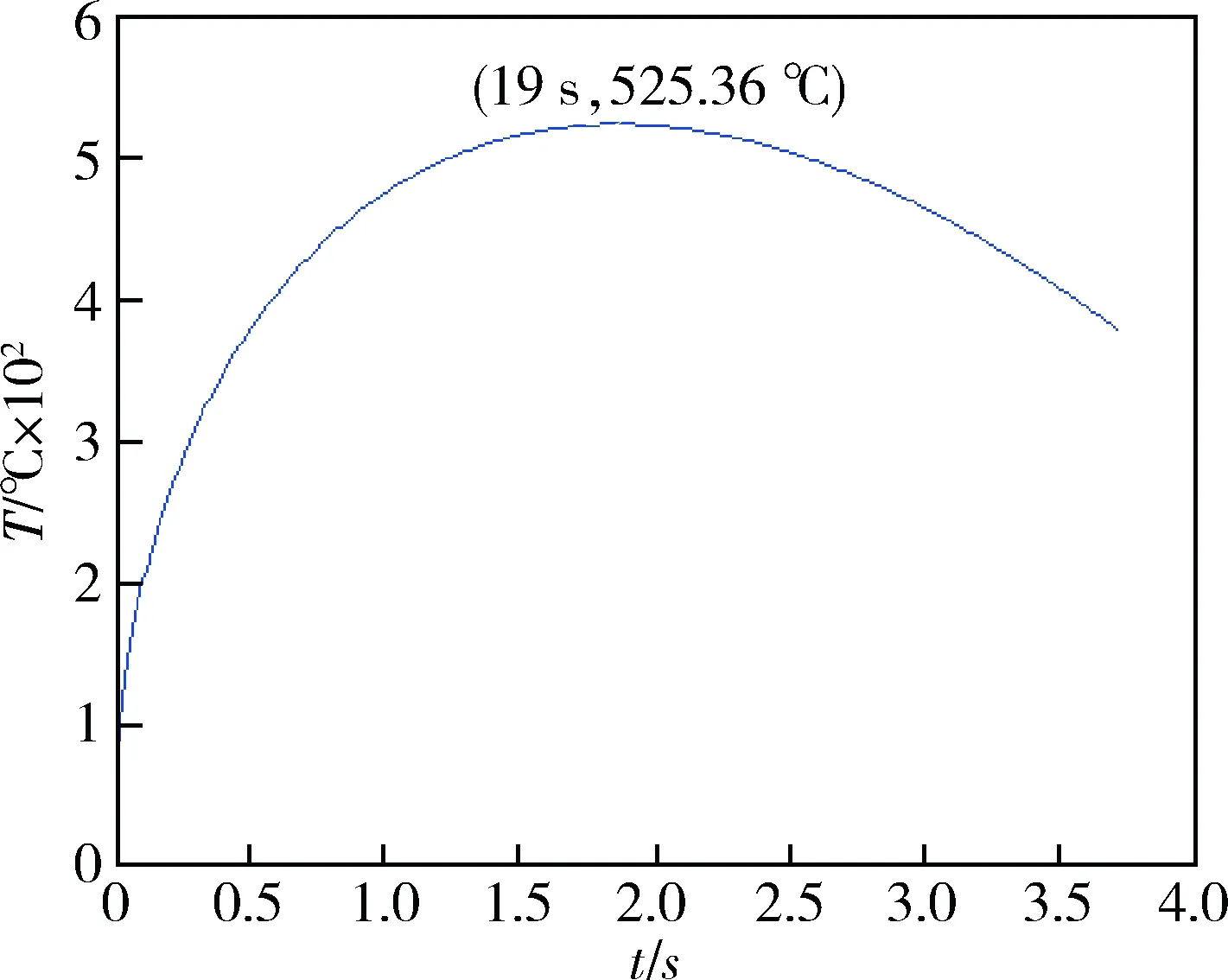
图2 制动盘表面温度曲线
从图2可以得到:初始时刻,由于制动盘的速度最大,输入的热流密度产生的热量导致温度急剧上升,随着时间的积累,制动盘温度不断上升,约1.8 s时达到最大,为525.36 ℃;1.8 s之后,制动盘的角速度已经很小,热流密度引起的温升不足以抵抗对流换热引起的热量交换时,制动盘的温度随时间下降.约3.7 s制动结束车轮抱死后,制动盘和摩擦衬片与空气、散热筋板自然对流换热,温度渐渐降下来.
2 制动盘温度场有限元分析
本研究使用Ansys Workbench热分析瞬态求解模块对某履带车辆盘式制动器的制动过程进行瞬态热分析.
设定以下假设条件[14]:1)装甲车辆制动过程分为制动力矩增加过程(0.2 s)与匀减速过程(3.524 6 s),摩擦副间压力先增加后恒定;2)摩擦副间压力分布均匀,整个制动过程摩擦系数不变;3)制动生成的摩擦热产生在摩擦副表面,并以热流密度的形式传入摩擦片内部;4)忽略除对流、辐射形式以外的其他散热;5)制动盘结构中心对称,仿真中的热分布同样中心对称;6)制动盘材料各向同性.
2.1 分析前处理过程
制动盘中心对称[13,15],为减小计算量与运算时间,这里只取1/20的制动盘进行分析,如图3所示.为便于网格划分,删除模型的圆角、倒角,同时在1/20制动盘模型的两侧边界设定为对称约束.
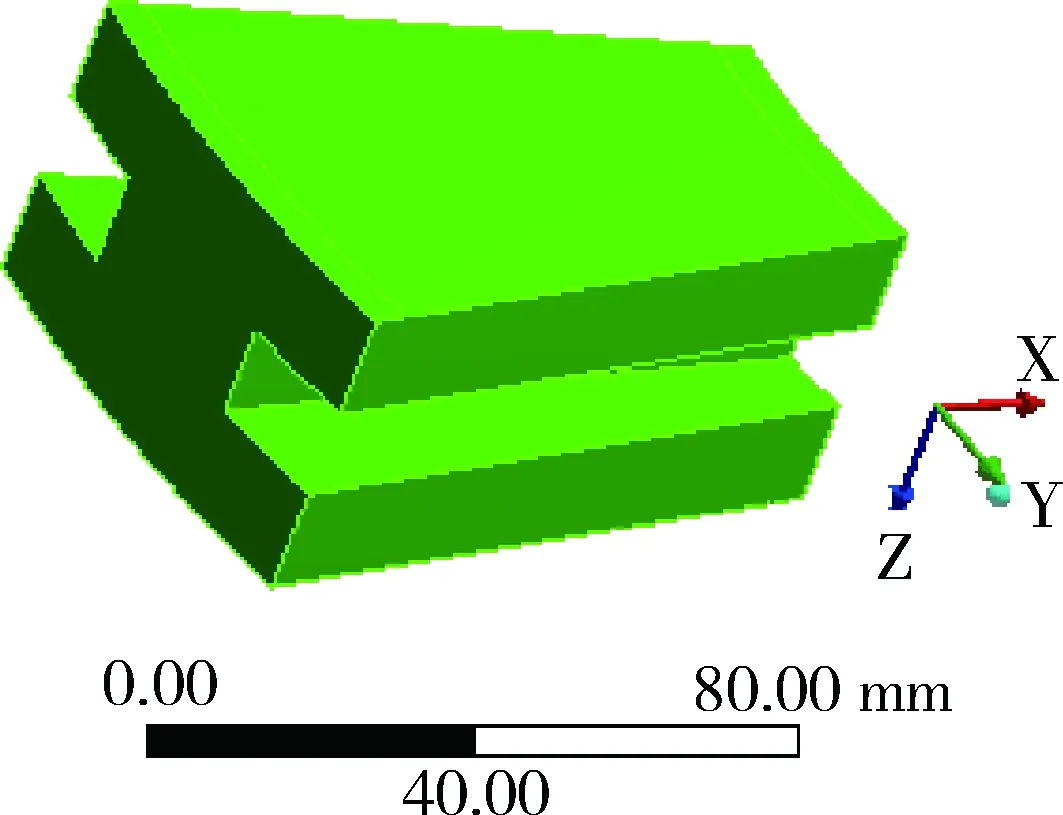
图3 1/20制动盘
本研究采用Meshing中扫掠网格划分法划分网格(Sweep),实现了可扫掠六面体与楔形单元的有效划分,同时增加网格划分精度,可以有效提高有限元的计算精度.
对盘式制动器温度场的有限元分析的核心问题为热负荷的施加.这里选择在制动盘与制动片接触面上直接加载热流密度,在时间和空间的分布上可以确定完整的热源边界条件.
2.2 计算结果分析
取几个时刻制动盘温度云图如图4所示.
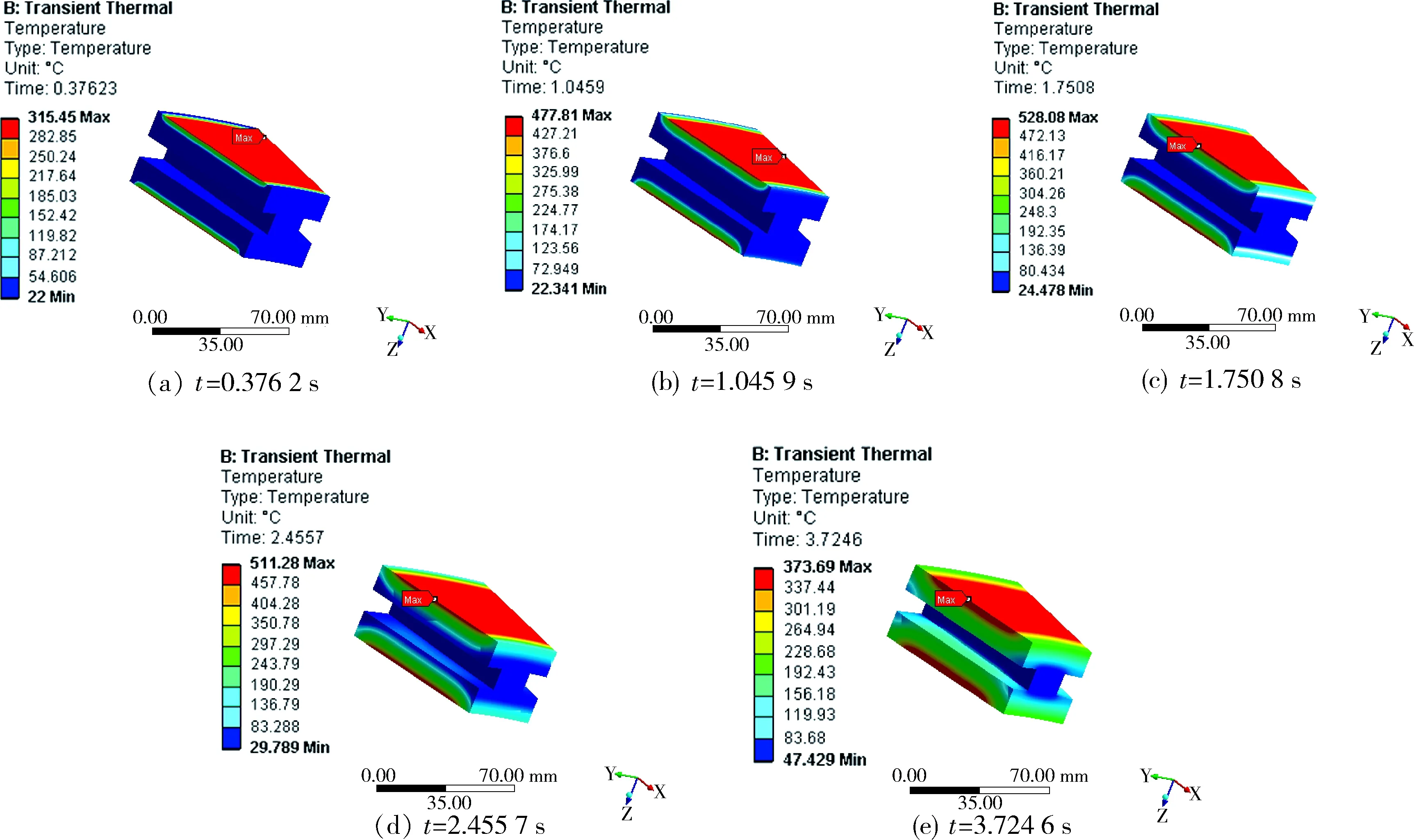
图4 不同时刻制动盘温度云图
各个时刻制动盘最高温度曲线如图5所示.
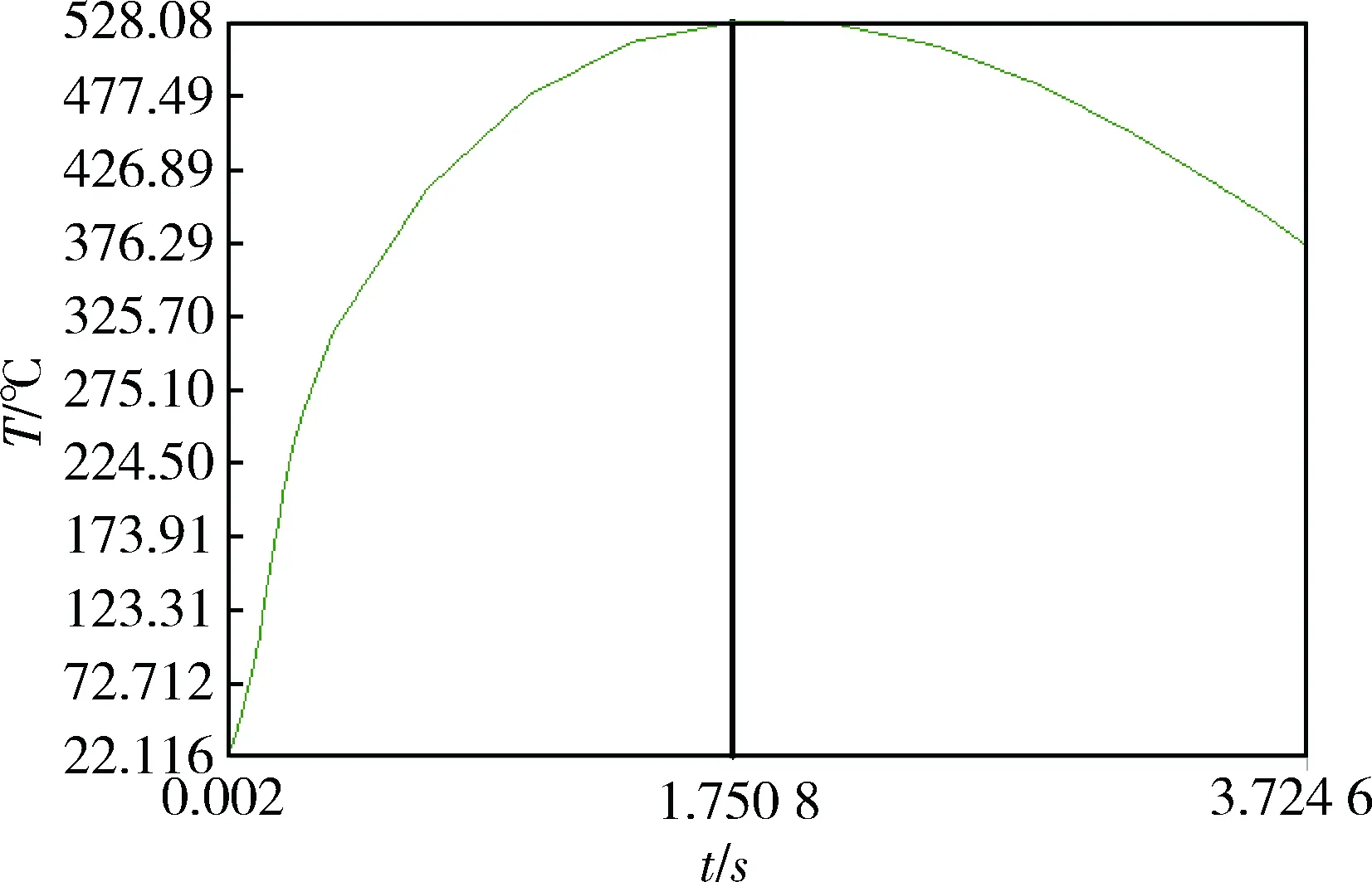
图5 制动盘最高温度随时间的变化曲线图
从图4中可以看出:制动盘表面的温度场呈环状分布,因为仿真中热量是以热流密度的形式输入到摩擦表面,因此相同半径处的温度场是相同的.随着时间的增加,热量不断向制动盘内部传递,内部温度不断上升.制动盘表面温度中间部分最高,内外径部分较低.内径温度较低是由于摩擦热生成速度随切向速度的增大而增大,内径部分摩擦速度相对较低造成的,外径温度较低是由于外径边缘处的对流换热条件比其他部分良好造成的.这样也导致了同一时刻的最高温度出现在制动盘表面的中间部分.
由制动盘最高温度变化曲线图5可见:制动刚开始时,温度急剧上升,但温升速率逐渐减小,且最高温度528.08 ℃并不出现在制动末尾,而是在制动中间1.750 8 s时刻,这与理论计算求出的温度变化曲线图2结果大致相同.制动的初始阶段,制动盘与制动片之间的相对摩擦速度最大,由于热流密度的大量输入产生的热量导致制动盘温度急剧上升,随着时间推移,制动盘最高温度不断上升.但随着制动过程的进行,制动盘的角速度迅速降低,直到制动盘能量的输入引起的温升不足以抵抗对流换热引起的热量交换时(t=1.750 8 s),温度开始下降,3.724 6 s后刹车抱死,制动盘和摩擦衬片与外界对流换热,温度逐渐降低.
3 热应力应变有限元分析
3.1 仿真边界条件
在制动器的工作过程中,由于温度场的剧烈变化,会引起制动盘内部热应力的变化.在实际制动过程中制动盘所受的机械载荷包括由于旋转产生的离心力、振动载荷、压装载荷.根据经验,与摩擦生热产生的热应力相比,这些因素对制动盘总应力的影响很小,可以忽略不计.热应力是由于节点温度的升高,制动盘内不均匀膨胀受到约束而产生的应力.
仿真边界条件为:
1)si|t=0=0,即初始状态位移为0;
2)Δsi=0(i=1,2,3,4,5,6),制动盘内侧与传动系统连接部位无相对位移;
3)s3=0,制动盘制动面Z向平动位移为0;
4)φleft=φright,对称边界条件.其中:i分别表示X、Y、Z、ROTX、ROTY、ROTZ6个自由度.
引入前面计算得到的全盘制动器温度场分布,施加上述边界条件进行热应力分布计算.为了得到最大的变形与应力,导入制动盘t=1.750 8 s处的最高温度场.
3.2 热应力分析
图6为制动盘热应力云图.图7为制动盘热应力等值线图.制动器由于温度变化引起的最大应力位于制动盘表面.从图中可以看出制动盘表面的热应力出现均匀交替的变化规律,最大应力处在整个制动盘上的位置的变化规律与实际中制动盘的最大磨损处的规律一致,表明制动盘工作时的磨损与其热应力存在联系,制动盘的使用寿命与其工作过程中的热应力息息相关.制动盘工作时的最小应力出现在制动盘外边缘散热孔外环口附近,因此制动盘外侧应力梯度极大,可能会产生局部热弹失稳现象.
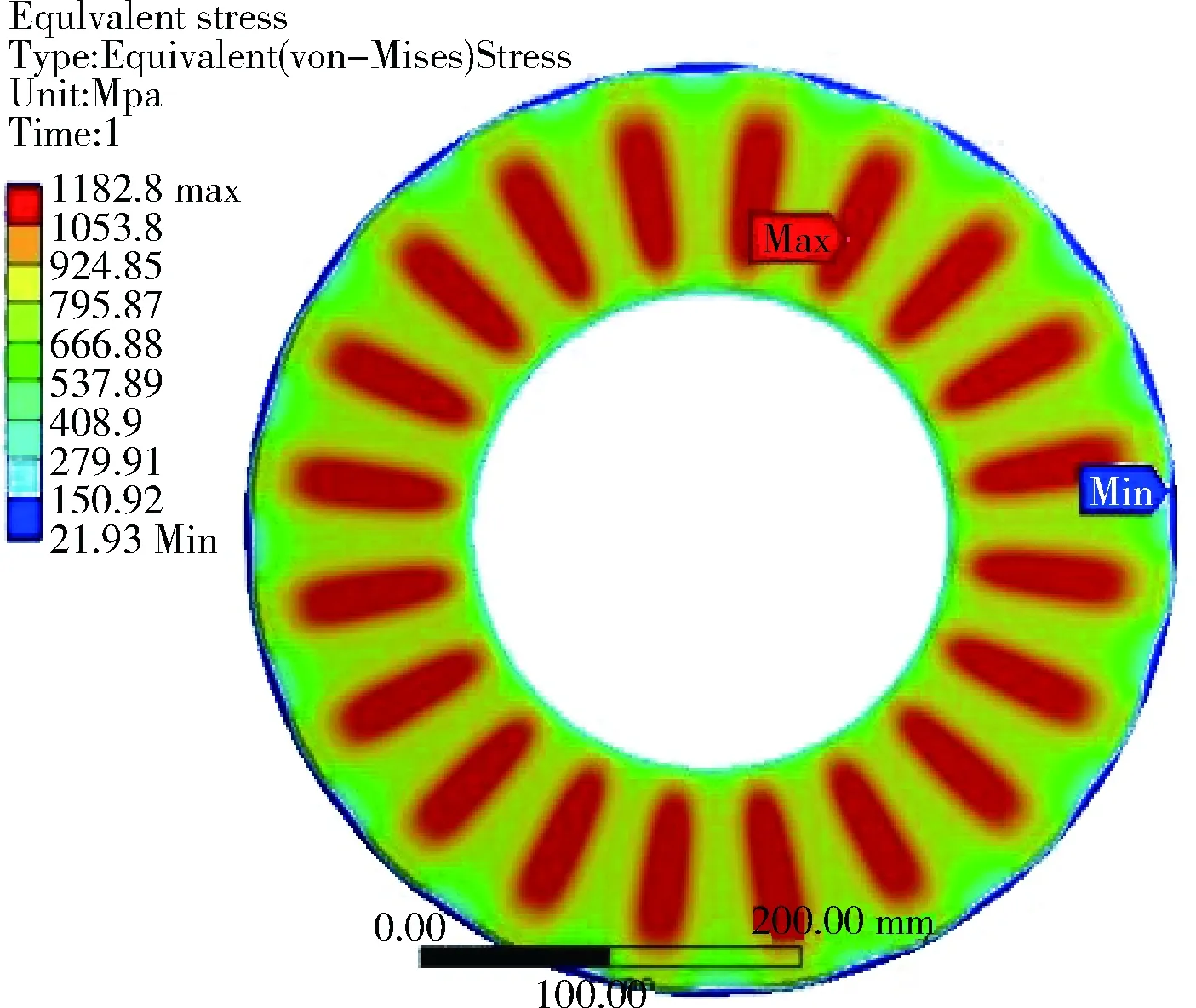
图6 制动盘热应力云图
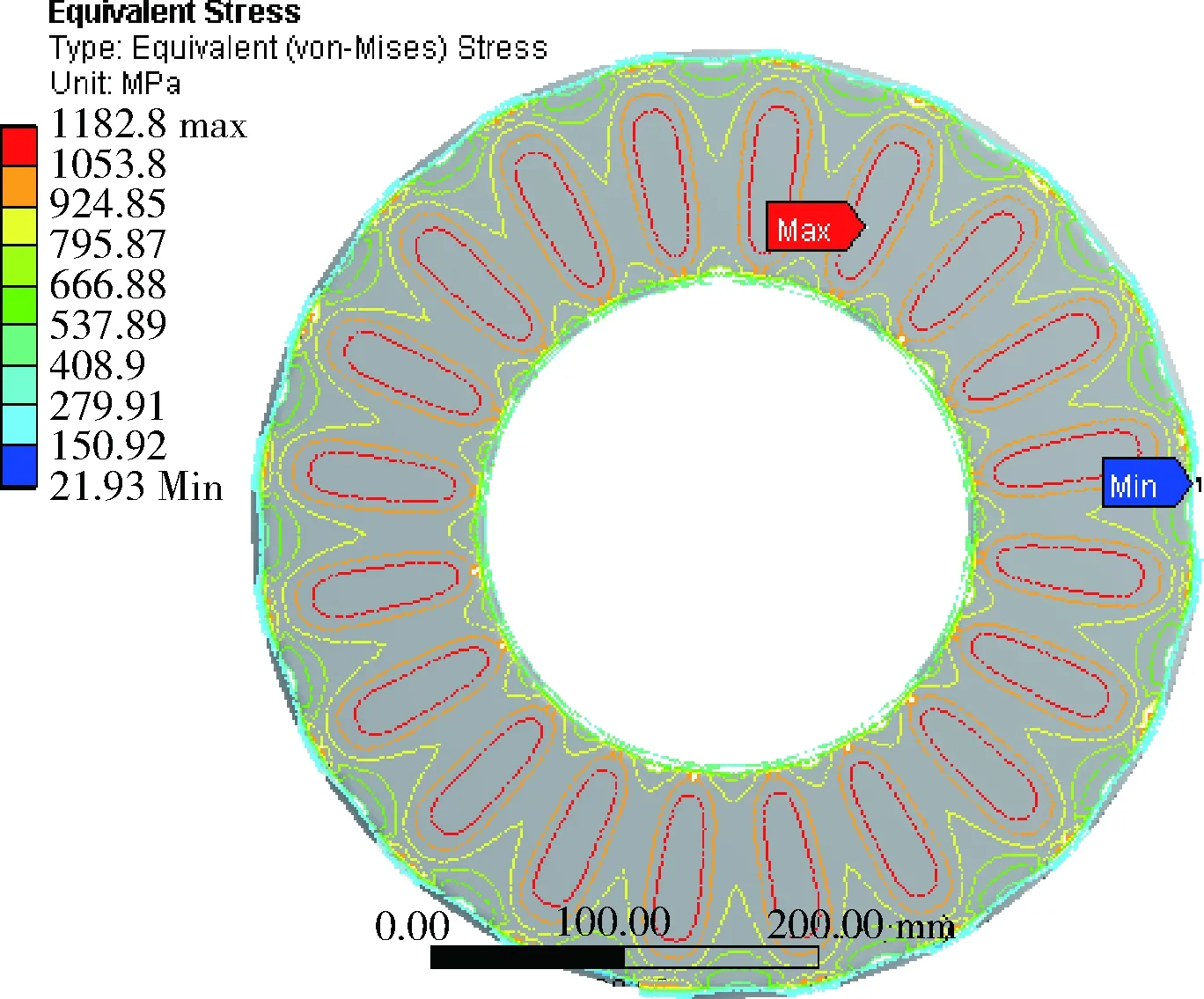
图7 制动盘热应力等值线图
3.3 热变形分析
制动盘在最高温度处受热膨胀后的实体变形如图8所示.单元位置的变化反映了受热后实体各点位置的变化,从图8中可以得到最大变形位移可达0.247 mm.从总位移变化的等值线图9中可以更加清楚地看到热变形位移变化的趋势,内侧由于事先给定了零位移约束,其总位移变化最小,位移等值面由内侧到外侧移动趋势不断增强,并在外侧上方达到最大,与实际制动过程中摩擦片的热应力分布状况相符.
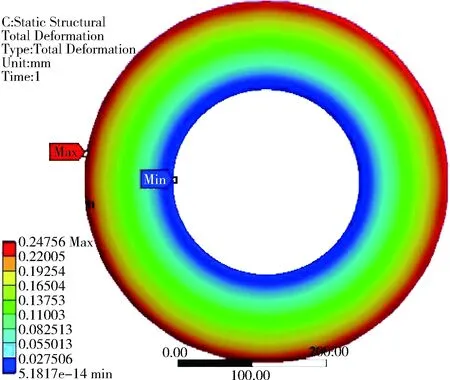
图8 制动盘热变形位移云图
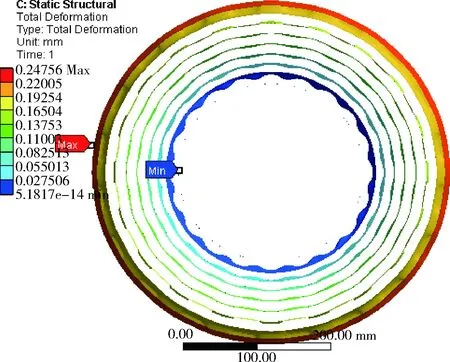
图9 制动盘热变形位移等值面图
4 结 论
首先从理论上通过研究某型履带车辆紧急制动过程中制动盘的热流密度随时间的变化关系、及对流换热系数的计算公式,得到了制动盘表面在制动过程中最高温度随制动时间的变化曲线,然后利用有限元法对制动盘的温度场进行仿真分析,结果发现最高温度的变化曲线与理论研究一致.
同时,利用有限元法还得到制动过程中制动盘温度变化的机理:制动初始阶段,由于相对摩擦速度最大,摩擦产生能量最多,导致制动盘温度急剧上升,随着制动过程的进行,温度上升的速度逐渐降低,这是由于相对摩擦速度降低引起的.制动盘的最高温度达到525.36 ℃.当机械能转化为内能的速度小于对流散热时,制动盘的温度开始逐渐降低.最后根据制动盘工作时的温度场分布,通过有限元仿真分析发现制动过程中制动盘外侧的热应力最大、热变形也最大,最大值为0.247 mm.
[1] 闫清东.坦克构造与设计下册[M].北京:北京理工大学出版社,2007.
[2] 朱永梅,朱玉君,王新国,等.盘式制动器热结构耦合分析[J].江苏科技大学学报(自然科学),2015,29(3):267-271.
[3] 罗继华,杨美传.动车组拖车制动盘有限元热分析[J].铁道车辆,2009,(4):22-25.
[4] 王 营,曹献坤,姚安佑,等.盘式制动器摩擦片的温度场研究[J].武汉理工大学学报,2001,23 (7):22-24.
[5] 马保吉,朱 均.紧急制动过程动态摩擦热源模型[J].机械科学与技术,1998,17 (5):698-700.
[6] Kiple RC, Mackin TJ, and Noe SC. Thermal cracking in disc brakes[J]. Engineering Failure Analysis, 2002(9):63-76.
[7] 周志勇,张 宏,樊启蕴.盘式刹车制动盘的高温失效机理和寿命计算[J].石油机械,1998,(1):29-31.
[8] 管原繁夫.轮对的设计[J].国外铁道车辆,1983,(1):17.
[9] 刘 艳,陈燕峰,吴跃成,等.客车盘式制动器温度场仿真分析[J].浙江理工大学学报(自然科学版),2017,37 (3):389-393.
[10] 宁克焱,李洪武,张洪彦.干片式制动器的研究与发展[J].车辆与动力技术,2004,(1):16-22.
[11] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社,1998.
[12] L.鲁道夫,编.张蔚林,陈名智,译.汽车制动系统的分析与设计[M].北京:机械工业出版社,1985.
[13] 闫安志,徐 晖.ER制动器温度和应力场的ANSYS分析[J].机械科学与技术,2003,22(4):556-557.
[14] 杨 强.列车制动盘温度场和应力场仿真与分析[D].北京:北京交通大学,2009.
[15] 闫清东,李宏才,唐 衍.有限元法在湿式多片制动器温度场研究中的应用[J].汽车技术,2001,(2):13-17.

