履带板三维力解耦算法研究

韩 庆， 魏来生， 贺力朋

(中国北方车辆研究所，北京 100072)

准确获取履带传递的各个方向的力，对于开展整车动力学分析、解决车辆行驶过程脱带问题、匹配行动系统性能、做好行动系统零部件优化设计等均具有非常重要的意义.目前我国还没有进行履带动态力测试的能力.履带式坦克装甲车辆行驶过程中履带所受的三维动态力，包括履带板所承受的横向力、压力以及履带板之间的拉力.

在测试过程中，由于受履带本身的空间尺寸和结构形式限制，组成测量三维力的电桥的应变片只能布置在履带板金属表面上，这就导致了各个电桥输出信号之间相互影响，存在维间耦合，因此通过电桥输出的电压无法直接换算出履带板三维力，这种耦合也会对测量精度产生影响，因此必须想办法消除维间耦合，实质上就是将Ui=f(FXFyFz)关系函数通过各种算法，实现对各分力的准确测量.

消除或抑制耦合的方法主要有两个，一个是消除耦合产生的根源，即传感器的制造工艺等诸多问题，一般很难解决；二是利用标定矩阵，采取模拟或数字信号处理方法消除维间耦合，这种方法被广泛采用.目前国内外对维间耦合问题的研究颇多，但是许多解耦理论由于设计理论和计算过于复杂，很难用于工程化问题，本研究就履带板三维力解耦方法进行论述.

1 多维力传感器的解耦公式及基本形式

1.1 多维力传感器的解耦原理

多维力传感器解耦公式都是多项式形式的，基本分为两个类型，一个是显式公式，传感器的载荷可直接用各分量的信号增量乘以相应系数后相加得到；另一种是隐式公式，公式的两边都有包含载荷的项，需要使用迭代算法计算传感器的载荷值.

显式公式的用法比较简单，因此应用更为广泛.一般将公式用矩阵形式表达，更为直观和易于计算.

公式的拟合方法主要是传统的最小二乘法、高斯消元法和相对较新的多项式响应面法.本研究使用多项式响应面法.

多项式响应面是一种比较成熟的模型，在优化领域、实验数据处理领域应用广泛.假定参数是n维向量，该向量是待求函数的自变量，二者存在的函数关系为y=y(x).尽管待求的函数可能找不出准确的表达式，但是，只要给定了参数值或设计点值，即取定了一个样本点x(j)，总可以通过实体的或数值的试验得到相应的性能值y(j)=y(x(j))，这是对应一个参数值或样本点值的一个响应值.如果做了足够多的试验，例如n个试验，那么我们就可以利用n个样本点及其n个响应，利用待定系数的方法求出函数y=y(x)的近似函数y′=f(x).f(x)为需要构造的响应面函数[1].利用该响应面函数，即可从试验参数值求得待求的参数.本研究中就是利用响应面函数将试验得到的电桥输出电压转换成履带三个方向的载荷.

实际中，根据工程经验，通常选取多项式的形式.通常一阶多项式响应面模型误差较大，而高阶多项式虽然精度较高，但由于其包含较多的项，计算量也随之增长，拟合的计算过程会更复杂.根据响应面函数表达式在能够描述真实函数的前提下应尽可能简单[1]的原则，在很多工程实践中，二阶多项式响应面模型应用最为广泛，因此本研究选取含交叉项的二次多项式的响应面函数形式.即

(1)

根据式(1)可知模型中含有10个待估系数.类似的，对于n元二阶多项式待估参数的个数为：

nrc=(n+1)(n+2)/2.

(2)

待估系数需要ns组试验点来确定(ns≥nrc)，进而确定待估系数值的大小.将式(1)写为向量积形式

f(xi)=Xiβ.

(3)

式中：Xi是由样本点xi构成的行向量；i=1,2,...,n.

由于式(3)要满足如下条件

f(Xi)=yi.

(4)

因此写成矩阵的形式为

X·β=Y.

(5)

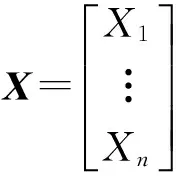
因为响应面函数是近似函数，所以根据式(5)计算的Y值与试验得到的响应值间存在误差.利用最小二乘原理使误差的平方和最小，即

S(β)=‖ε‖2=(Y-Xβ)T(Y-Xβ).

(6)

使S(β)最小的的必要条件为

S(β)=‖ε‖2=
((Y-Xβ)T(Y-Xβ))=
2(Xβ-Y)TX=0.

(7)

可求得

β=XTX-1XTY.

(8)

式(8)为X列满秩时得到的最小二乘解.最终将式(8)代入式(1)可得多项式拟合模型.

1.2 基于响应面法的履带板三维力解耦

履带板三维力响应面函数中，n=3，根据式(1)可知

(9)

设计变量分别为VFx，VFy，VFz，待求函数为

(10)

共进行ns组试验.假设β0=0，将每组标定试验得到的样本点代入式(3),可得到响应函数值：

(11)

根据式(7)利用最小二乘原理使误差的平方和最小，可得

(Xβ-Y)TX=0.

(12)

其中

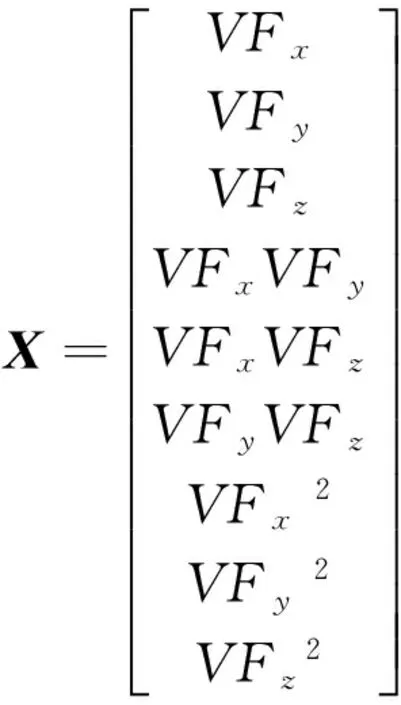
将标定数据代入式(8)，可得到β.

2 履带板三维力静态线性解耦方法

考虑到可测试履带板的解耦算法既要实现消除维间耦合的目的，又要满足可用于实际工程问题中，且可操作性强.所以重点研究了履带板三维力静态线性解耦的方法，即基于静态线性标定和响应面法的解耦算法.

2.1 履带板的标定

最传统的多维力静态解耦方法是基于静态线性标定试验的，因此履带板三维力解耦首先也要开展标定工作.

根据测试范围，选择n个标定点，分别对每个方向施加载荷.具体如下：

1)拉力标定.

试验开始，由履带刚性试验台施加拉力，逐步增加到100 kN拉力，然后再逐步卸载至履带全松(因为有履带自重，所以不能完全卸载到0 kN).测试不少于10个载荷值，读取可测试履带板采集的数据.

2)横向力标定.

试验开始，由履带刚性试验台施加16～17 kN的预拉力，然后通过横向力加载装置从0 kN逐步增加到50 kN的横向力，最后再逐步卸载至0 kN.测试不少于10个载荷值，读取可测试履带板采集的数据.

3)压力标定.

试验开始，由MSP250kN试验台施加压力，从0 kN逐步增加到100 kN的压力，然后再逐步卸载至0 kN，测试不少于10个载荷值，读取可测试履带板采集的数据.

在一个标定点上只施加一个载荷，会同时得到3个通道的输出信号.只有与施加载荷方向一致的那个通道的输出信号，才能反映履带板在该方向上受到的力，其他两个通道的输出信号只反映施加的力在那两个方向耦合的输出结果.

记录每个通道的输出，得到履带板3个方向上标定的时间-电压曲线，如图1、图2、图3所示.

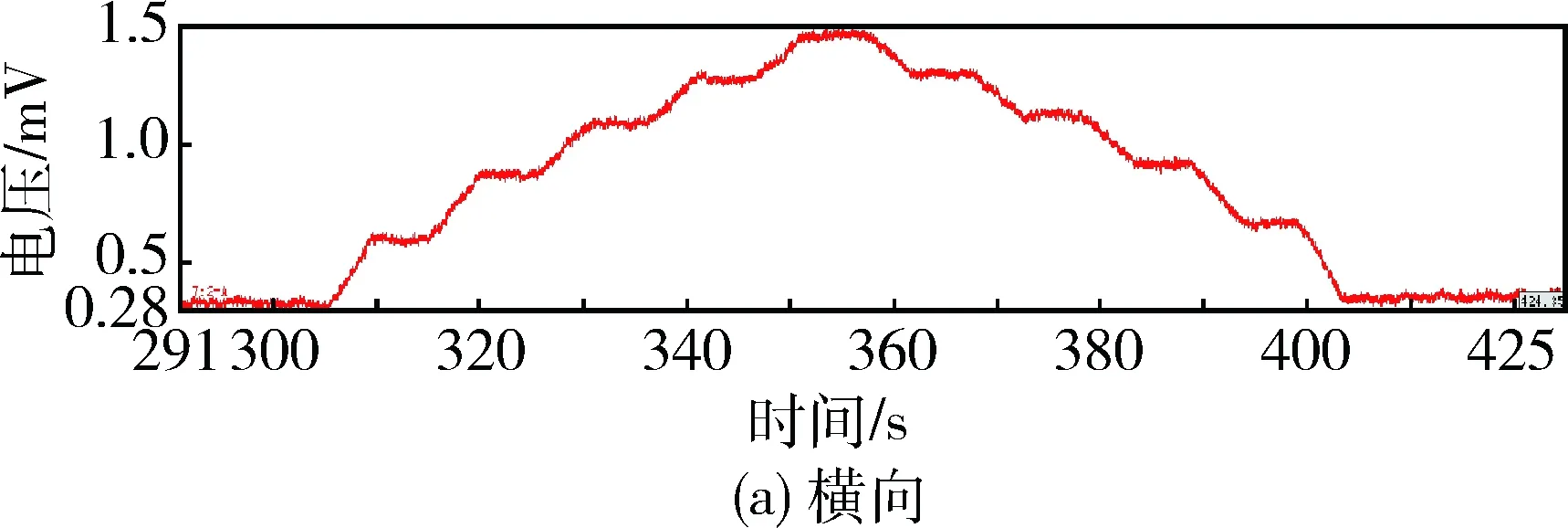
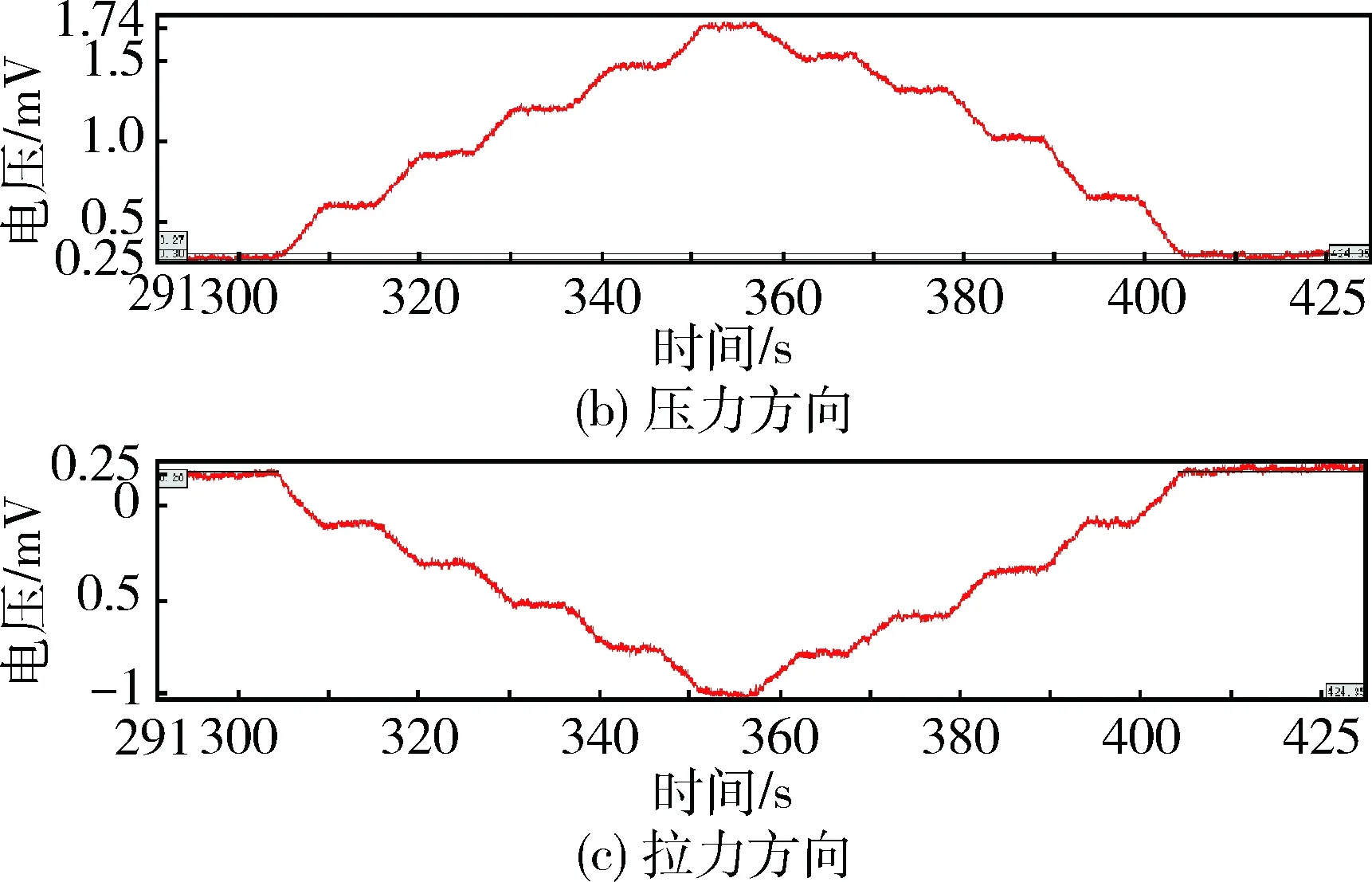
图1 压力方向加载时三个电桥时间-电压曲线

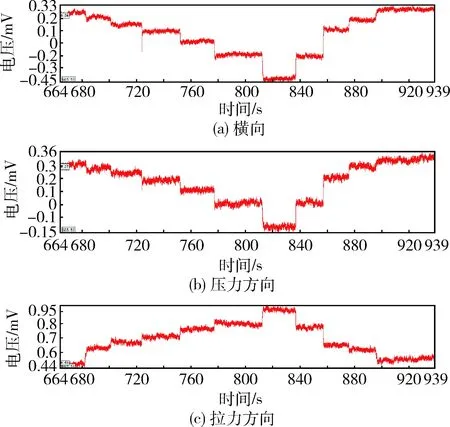
图2 横向力方向加载时三个电桥时间-电压曲线

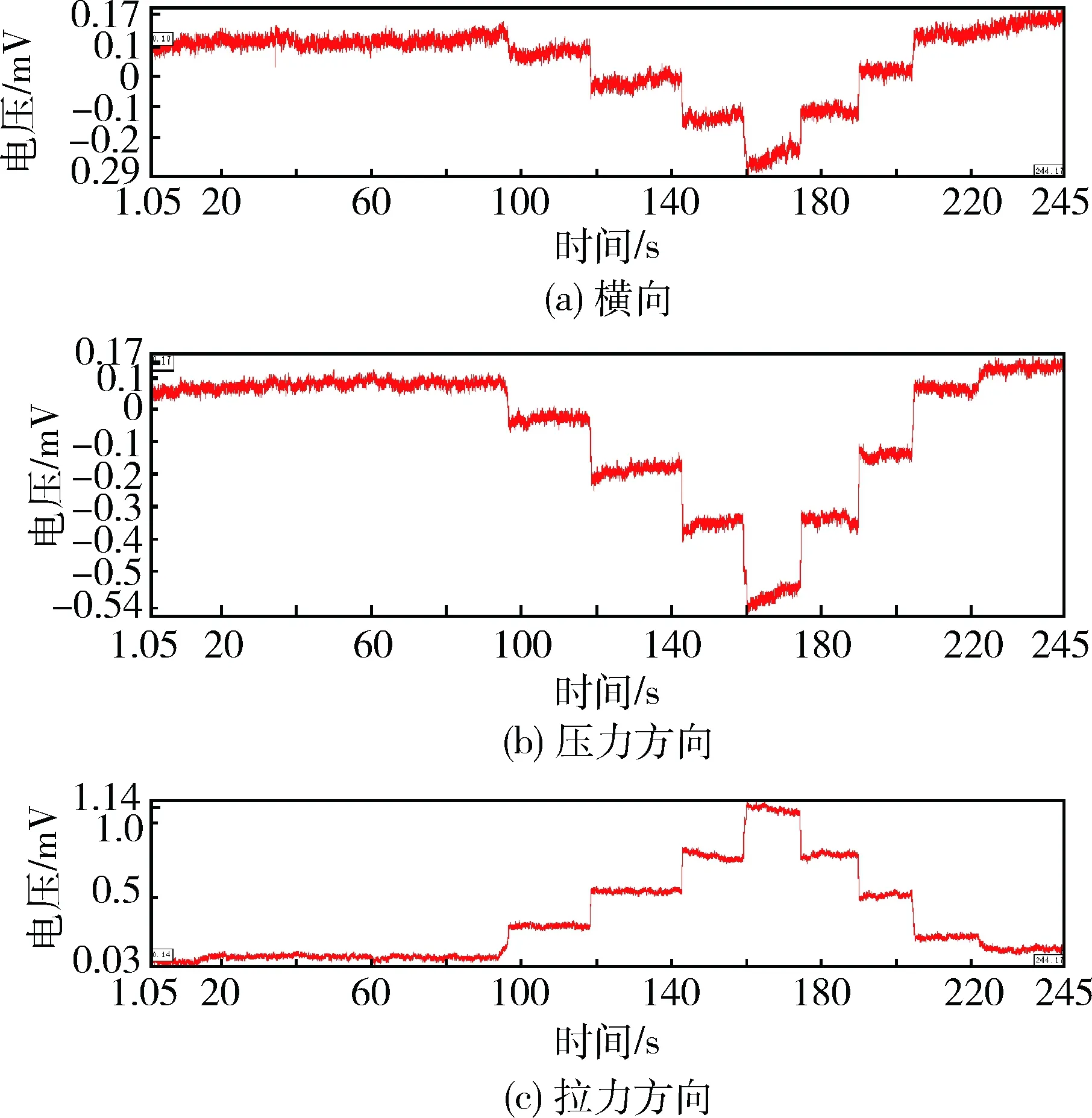
图3 拉力方向加载时3个电桥时间-电压曲线

具体各通道输出电压值和施加载荷数值如表1所示

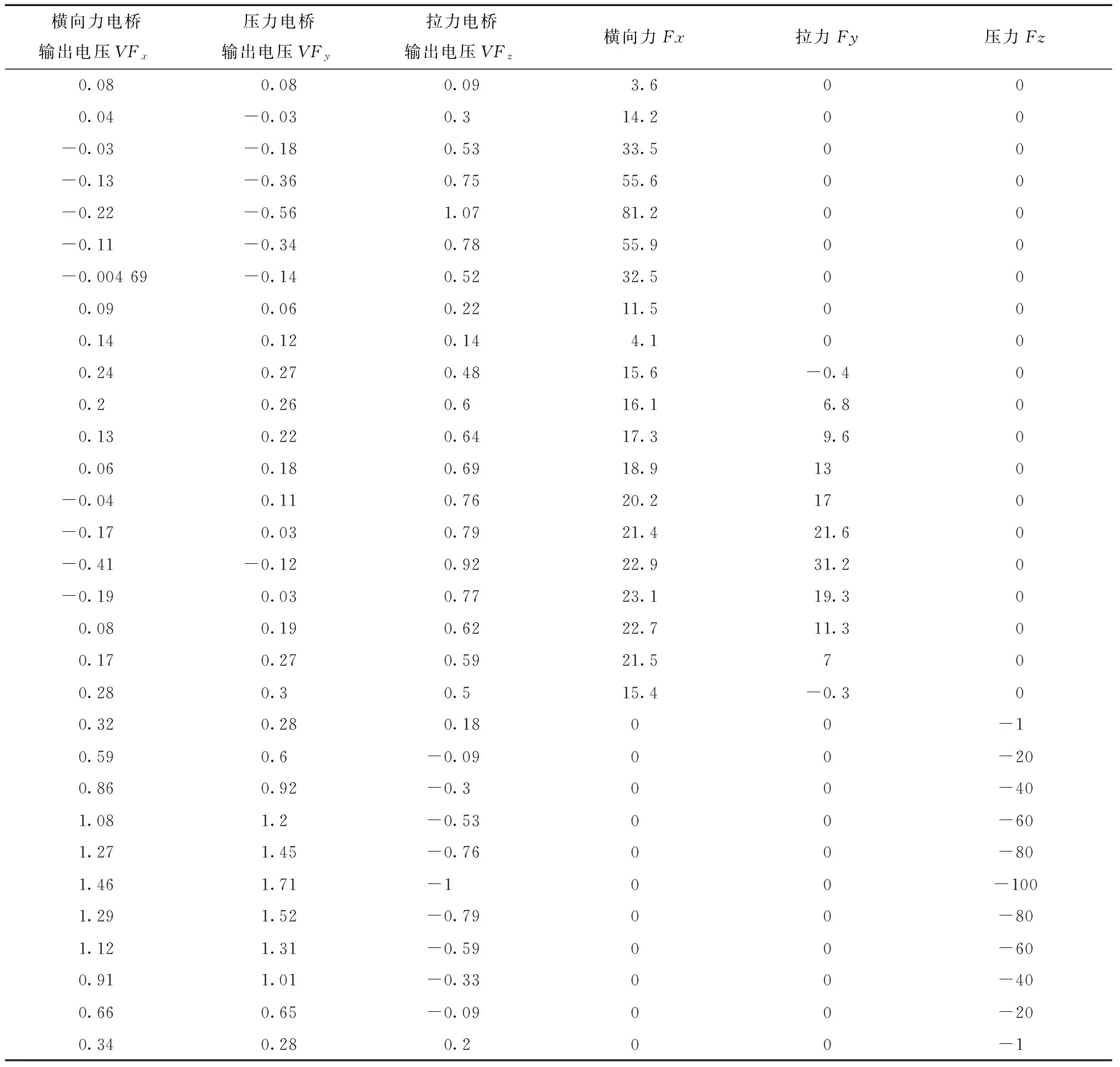
表1 各通道输出电压与相应施加载荷数值

2.2 基于标定结果的耦合矩阵的确定

为了尽可能精确地获得耦合矩阵，从多次标定结果中选择较好的作为计算耦合矩阵的依据.根据1.2节的算法，计算出的耦合矩阵为

得到可测试履带板的耦合矩阵后，代入式(9)可得到解耦后的履带板三维力值：

Fx=43.701×△VFx+42.693×△VFy-54.1938×△VFz+18.257×△VFx△VFy-346.17×△VFx△VFz-15.578×△VFy△VFz+161.68×△VFx2-13.1025×△VFy2+206.9203×△VFz2;

Fy=-3.788×△VFx+3.061×△VFy+1.821×△VFz-64.745×△VFx△VFy+120.892×△VFx△VFz+52.445×△VFy△VFz-54.6×△VFx2+15.8212×△VFy2-67.5484×△VFz2;

Fz= -47.0776×△VFx+10.502×△VFy+34.187×△VFz+59.069×△VFx△VFy-24.459×△VFx△VFz-51.271×△VFy△VFz+10.6595×△VFx2-11.81×△VFy2-11.14×△VFz2.

2.3 实际应用与结果检验

利用通过以上算法得到的可测试履带板的耦合矩阵，可得到实际测试过程中履带所受的实时载荷，如图4、图5、图6所示.实线加载值为实际施加的载荷值，虚线反算值为可测试履带板测试得到的载荷值，

根据测试结果，我们能够将可测试履带板3个方向的耦合关系分解开来，效果显著，误差是满量程的5%.

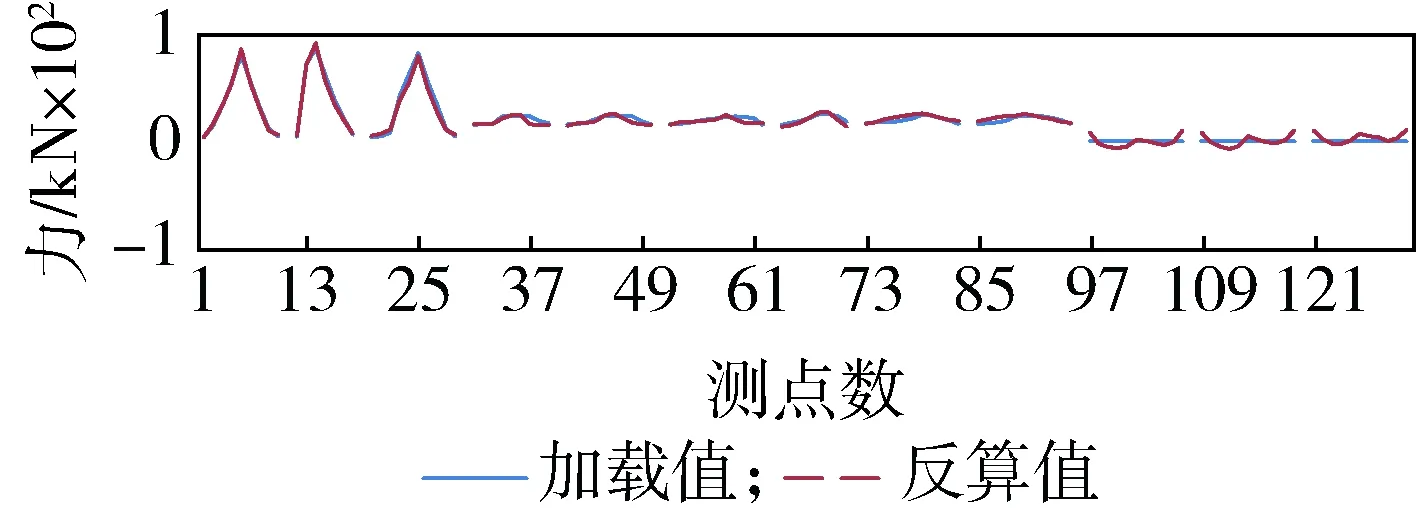
图4 拉力方向时间-载荷曲线(加载值与反算值对比)

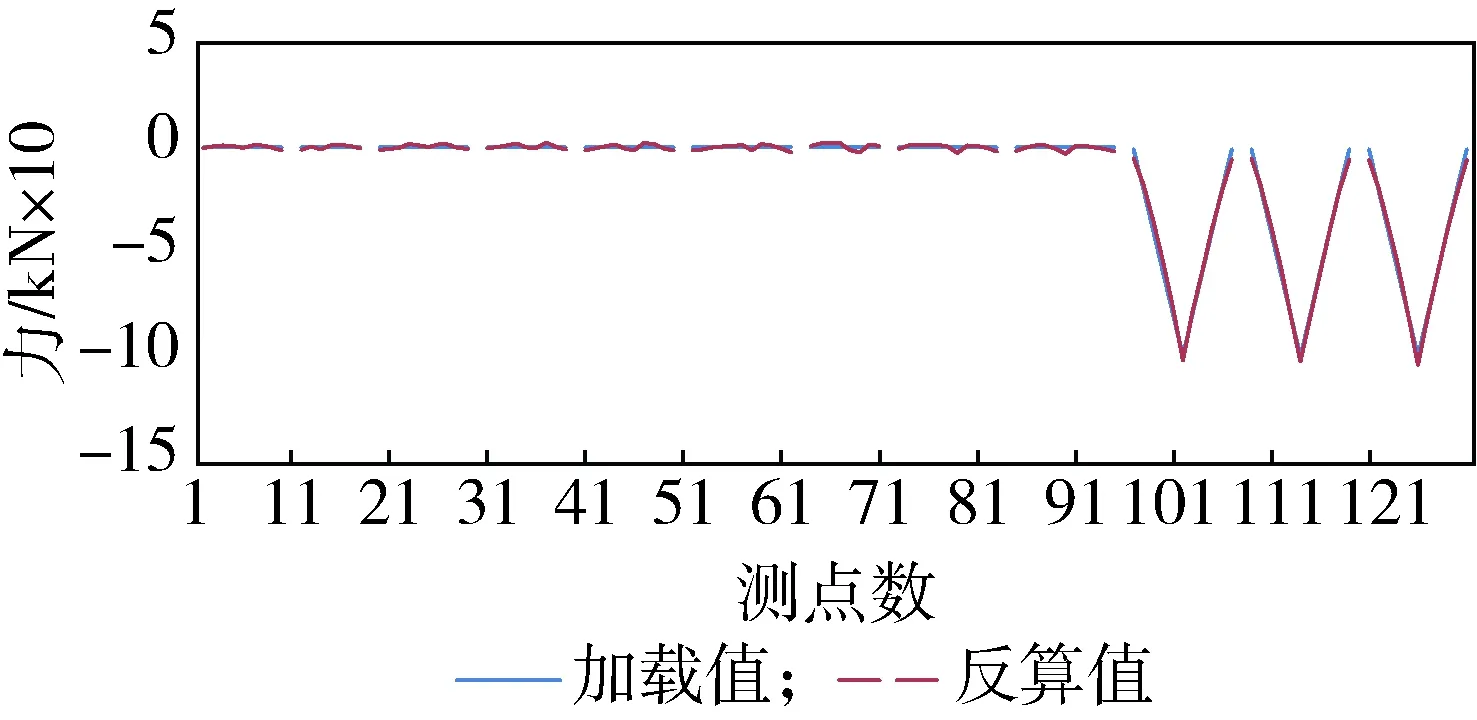
图6 压力方向时间-载荷曲线(加载值与反算值对比)

3 结束语

针对履带三维力测试过程中存在维间耦合的问题，采用基于静态线性标定和响应面法的解耦算法，提出了便于在工程应用中实现的解耦方法，解决了履带三维力之间的维间耦合问题，研究结论如下：

1)该方法是通过标定试验结果，建立近似显函数的形式对履带板三维力进行解耦计算的，易于工程应用;

2)利用该方法对履带板测试数据解耦得到的三维力与试验台施加的标准载荷对比，误差是满量程的5%；

因此，该方法适用于对履带板三维力进行解耦.

[1] 隋允康,宇慧平.响应面方法的改进及其对工程优化的应用[M].北京：科学出版社,2010.