一类欧拉积分公式与广义菲涅尔积分的计算*
邢家省,杨小远
(北京航空航天大学数学与系统科学学院,数学、信息与行为教育部重点实验室,北京 100191)
欧拉积分公式[1-3]是数学分析中的经典结果.费定晖等[1]利用对含参变量积分的求导方法,给出了欧拉公式的证明,但证明过程较为繁琐.华罗庚[3]指出,利用复围道积分方法也可得到欧拉积分公式,但这种证明所用的知识点较多.笔者发现,利用欧拉积分公式可以对几类重要的广义积分[1-14]给出统一的处理,而这几类广义积分在现有文献中是分别给予解决的,并且解决的办法相当复杂.笔者利用积分交换次序定理[1-7],给出了一类广义积分的计算结果,在导出结果的过程中完全是利用数学分析自身已有的理论方法.
1 一类欧拉积分公式的简便证明
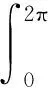
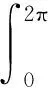
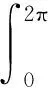
定理1仅出现在文献[4-5]中,原因是证明过程相当复杂,限制了它的传播.笔者给出了其简短的证明过程.

证明记
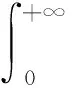

文献[1]中给出了定理2的证明,但证明过程较为繁琐.笔者利用对变量求导的方法,给出了简洁的证明过程,以便于理解和应用.

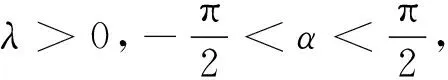
对-1 定理3得证. 利用定理2,可得如下结论: 定理6[1-3]设k>0,λ>-1,则有 定理7[1-3]设k>0,λ>0,则有 证明利用定理8、Γ函数的性质和余元公式,[1-5]可得 证明利用定理10 和Γ函数的性质及余元公式,[1-5]可得 定理12[1-4]设p>1,则有: 定理15[1-4,6]设k>0,-1<λ<1,则有 于是 利用定理15,可得如下结论: 利用积分交换次序的理论方法,可以证明 (1) 利用(1)式,可得如下结论: 定理17[2,15]设k>0,0<λ<1,则有 利用(2)式,可得 于是 证明利用贝塔函数的性质、Γ函数的性质和余元公式,[1-5]可得 文献[11-12]中,实际上是利用复围道积分的理论方法进行两道路上积分的转换,给出了一类广义积分的计算,其严格理论方法可见文献[3]. [1] 费定晖,周学圣.吉米多维奇数学分析习题集题解5[M].济南:山东科学技术出版社,1980:709-751. [2] 黄玉民,李成章.数学分析(下册)[M].2版.北京:科学出版社,2007:518-556. [3] 华罗庚,著.高等数学引论(第三册)[M].王 元,校.北京:高等教育出版社,2009:129-133. [4] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2002:819-831. [5] 常庚哲,史济怀.数学分析教程(下册)[M].北京:高等教育出版社,2003:344-359. [6] 匡继昌.Dirichlet积分九种解法的思路分析[J].高等数学研究,2012,15(4):61-66. [7] 白玉兰,陈述涛.一个二次广义积分的顺序交换问题[J].哈尔滨师范大学自然科学学报,1987,3(3):13-18. [8] FLANDERS H.On the Fresnel Integrals[J].American Mathematical Monthly,1982,89(4):264-266. [9] LEONARD I E.More on Fresnel Integrals[J].American Mathematical Monthly,1988,95(5):431-433. [10] 邢家省,杨小远,白 璐.两无穷区间上积分交换次序充分条件的改进及其应用[J].四川理工学院学报(自然科学版),2016,29(1):87-92. [11] 邢家省,杨小远.广义菲涅尔积分的积分交换次序计算方法[J].四川理工学院学报(自然科学版),2016,29(3):85-92. [12] 邢家省,杨小远,白 璐.菲涅尔积分计算中的一致收敛性的证明方法[J].吉首大学学报(自然科学版),2016,37(5):1-9. [13] 邢家省,杨义川,王拥军.菲涅尔积分的几种计算方法[J].四川理工学院学报(自然科学版),2016,29(5):88-96. [14] 邢家省,杨义川,王拥军.函数列的广义积分的极限定理及其应用[J].吉首大学学报(自然科学版),2016,37(6):1-9.

2 欧拉积分公式的直接应用
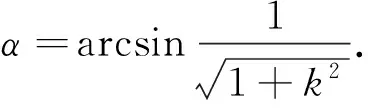
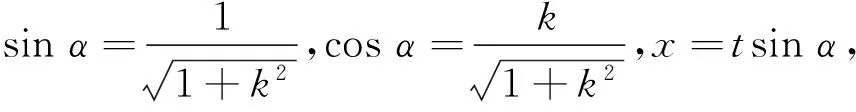

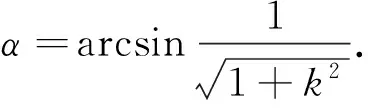
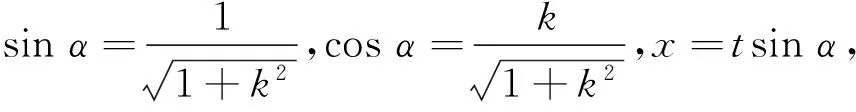


3 欧拉积分公式在广义菲涅尔积分计算中的应用
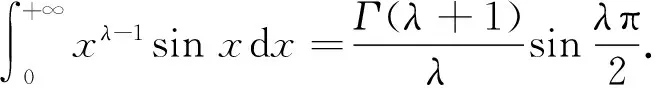

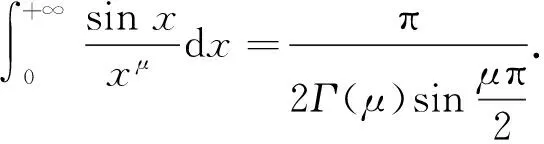



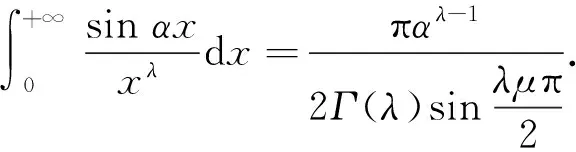

4 欧拉积分公式在一些广义积分计算中的应用