黏弹特性对模内微装配成型热流固耦合变形的影响

周国发，邓其春，江先念，段治锋，李斐斐

(南昌大学资源环境与化工学院，南昌 330031)

0 前言

(a)一次成型 (b)二次注射成型模腔 (c)二次成型 (d)模内装配微运动副图1 聚合物微型机械系统模内微装配成型原理Fig.1 In-mold micro assembly molding principle of polymer micro-mechanical systems

聚合物微型机械系统制造加工的共性技术问题是微装配技术，而微装配工序在夹拿聚合物微型件仍存在夹持面易损伤和易黏附的技术障碍，至今微装配技术仍是规模化微机械加工的技术瓶颈，模内微装配成型新工艺能解决这一瓶颈[1-9]。其成型过程见图1，先一次注射成型微型轴，待其冷却凝固后，移动可变组合模具左右二边的滑块，由微型轴的微装配面与可变组合模具重构二次成型微型块的模腔，再二次注射成型微型块，并在模内将微型块成型与微装配工序集成于一体。二次成型高温熔体流动移动前沿与预成型微型轴的微装配面接触时，在微装配界面会形成黏弹性热流固耦合冲击载荷，由此诱导微型轴变形，严重影响运动副微装配加工精度，导致成型废品率偏高。为此研究准确预测和精密调控其变形的理论与技术，方能实现模内微装配成型加工从目前偶然中求一成功的“摸索制造”向以“科学求质量、以技术保成功” 的全流程综合控制的工业化科学制造”飞跃。

1 黏弹性热流固耦合理论模型

1.1 动力学控制方程

预成型微型件变形的动力学控制方程如式(1)～(2)所示：

(1)

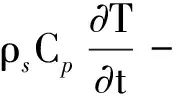
(2)

式中u——位移矢量，m

ρs——固体密度，kg/m3

t——时间，s

σ——应力张量，MPa

Fs——体力，kg·m-3

Cp——定压比热容, J/(kg·K)

T——温度，K

k——热导率，W/(m·K)

二次成型黏弹性熔体充填流动的控制方程如式(3)～(6)所示：

(3)

(4)

σ=-pI+τ

(5)

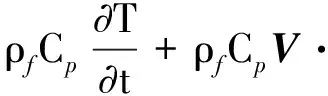
(6)

式中V——速度矢量，m/s

p——压力，MPa

I——单位矩阵

τ——偏应力张量，MPa

ρf——熔体密度，kg/m3

1.2 聚合物熔体与固体的本构关系

1.2.1 二次成型黏弹性熔体本构关系

微型轴产生弯曲变形的驱动力来源于微装配界面承受的黏弹性热流固耦合冲击载荷。在其作用下，微型轴在二次成型高温黏弹性熔体充填流动边界约束作用环境下产生变形。为此如何真实反映周围二次成型高温黏弹性熔体充填流动环境对微装配界面的边界约束作用和黏弹性热流固耦合冲击载荷是准确预测其变形行为的理论前提。

二次成型高温黏弹性熔体充填流动形成的流动弹性正应力τii对微装配界面形成弹性支撑边界约束作用，其剪应力τij则形成黏性拖曳剪切边界约束作用，为了科学刻画这一复杂微装配界面边界约束，二次成型黏弹性熔体充填流动的本构方程需采用黏弹性PPT本构模型[10-12]，如式(1)所示，其模型参数详见表1。

=2(1-ηr)ηD

(7)

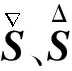
(8)

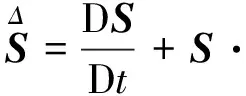
(9)

式中D——应变速率张量

η——聚合物熔体的总黏度，Pa·s

ηr——黏度比

η2——溶剂的牛顿黏度，Pa·s

ζ——材料参数

λ——松弛时间，s

β——材料参数

S——黏弹性偏应力张量

表1 PTT模型参数Tab.1 Parameters for PTT model

1.2.2 预成型微型轴热黏弹性应力应变本构关系

现将微型轴视为黏弹性体，则其热黏弹性本构关系为：

σ=[E](ε-εth)

(10)

(11)

式中 [E]——弹性矩阵

ε——应变张量

εth——热应变张量

E——弹性模量，MPa

X——温度影响因子

Tg——玻璃化转变温度，K

Δ——相变演化温度影响因子，K

式(11)中下标g表示玻璃态，r表示黏弹性高弹态。弹性模量模型参数详见表2。该模型方程(11)所预测的相变演化对PMMA材料弹性模量及泊松比的影响规律与文献[13]的实验结果吻合。

表2 弹性模量模型参数Tab.2 Parameters for elastic modulus model

1.3 边界条件

微装配界面黏弹性热流固耦合边界条件设置如式(12)～(15)：

ps=pf

(12)

(13)

Ts=Tf

(14)

σs·n=τf·n

(15)

式中n——单位矢量

2 黏弹性热流固耦合变形机理研究

2.1 模拟条件

本文以图1所示的典型微型移动机械运动副为研究对象，其有限元模型见图2。一次成型微型轴选用CM-205聚甲基苯烯酸甲酯(PMMA)材料，二次成型微型块选用M-201聚苯乙烯(PS)材料，并通过Arrhenus Law模型修正温度对熔体黏度的影响，其方程见式(16)，Arrhenus Law模型参数详见表3。

(16)

图2 有限元模型Fig.2 Finite element model

表3 Arrhenus Law模型参数Tab.3 Parameters for Arrhenus Law model

2.2 熔体黏度对微型轴热流固耦合变形的影响

现通过人为改变二次成型黏弹性熔体的黏度，研究其对微型轴黏弹性热流固耦合变形行为的影响。图3和图4为二次成型黏弹性熔体黏度对黏弹性热流固耦合诱导微型轴变形影响的模拟结果，研究结果表明微型轴的热流固耦合变形随着二次成型黏弹性熔体黏度的增大而增大，且与二次成型黏弹性熔体黏度呈线性正比关系。

2.3 机理分析

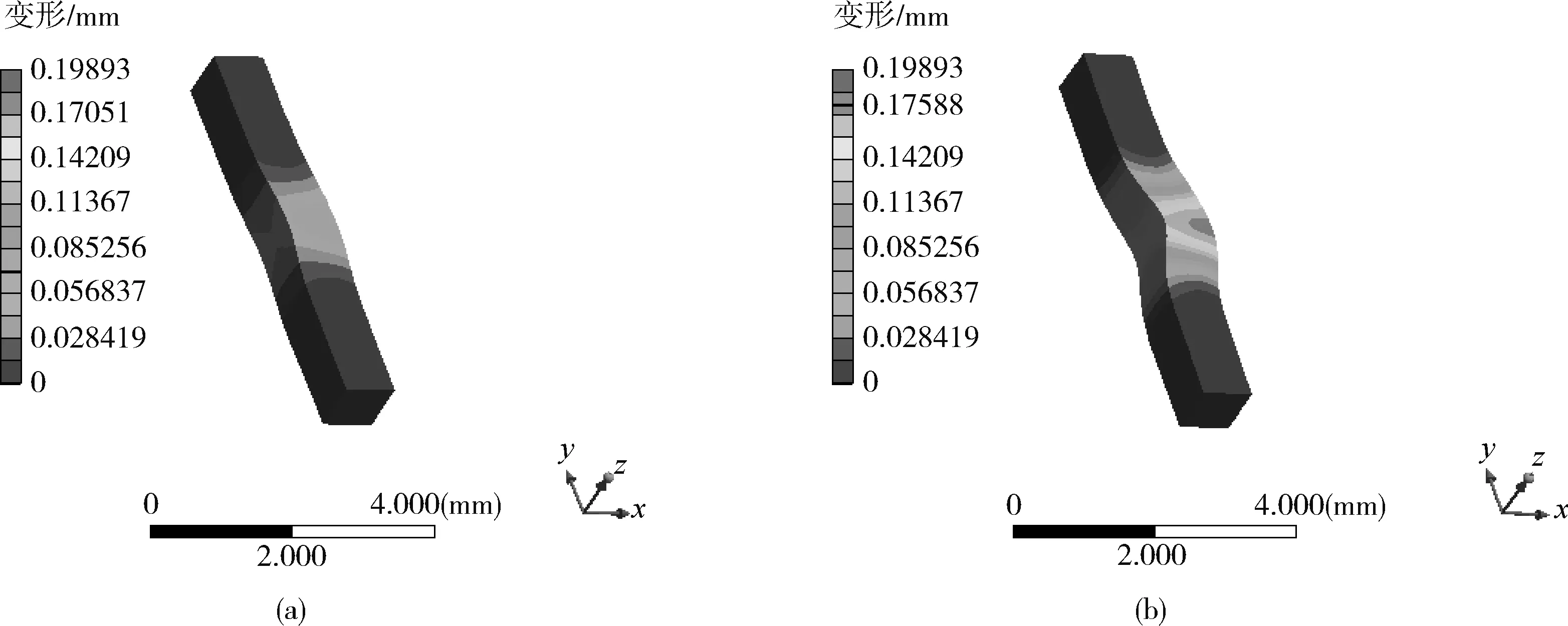
熔体黏度/Pa·s：(a)1 267 (b)3 267图3 熔体黏度对微型轴热流固耦合变形的影响Fig.3 Influence of melt viscosity on micro-shaft thermal-fluid-structure coupling deformation

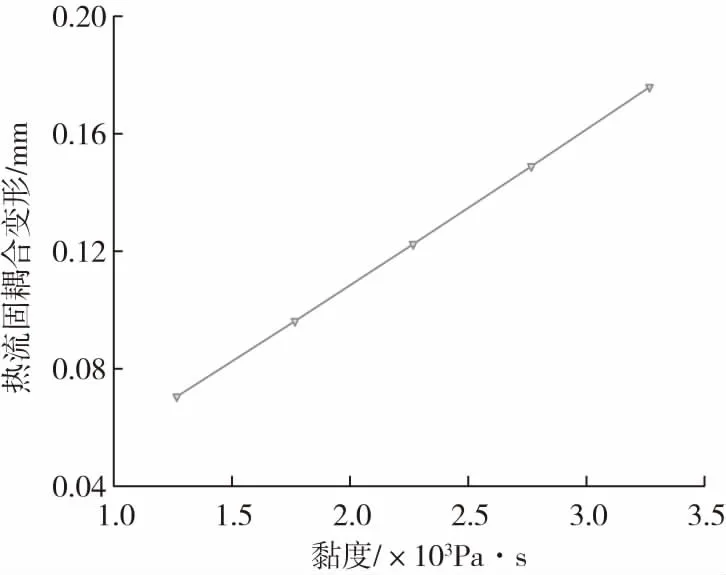
图4 微型轴热流固耦合变形与熔体黏度曲线Fig.4 Micro-shaft thermal-fluid-structure coupling deformation vs. melt viscosity

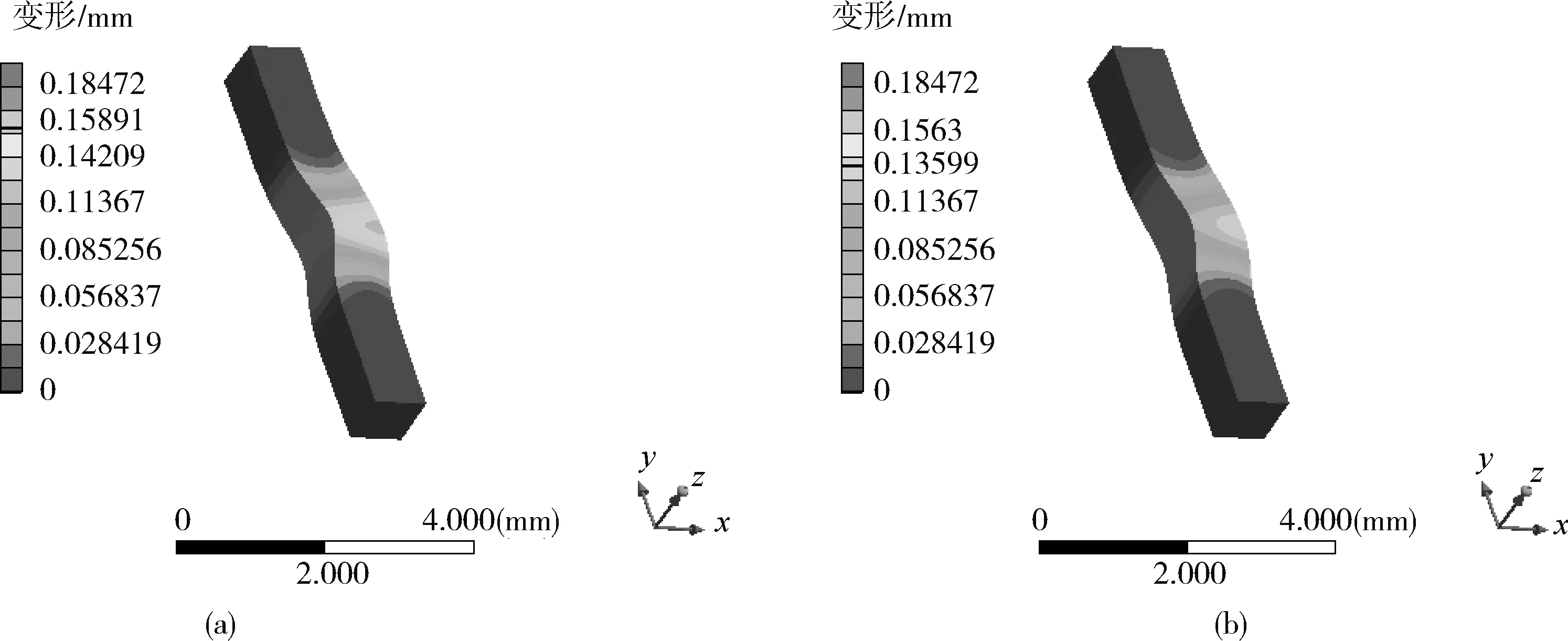
(a)载荷工况1 (b)载荷工况2图5 弹性支撑正应力对耦合变形影响(η=3267 Pa·s)Fig.5 Influence of elastic normal stress on micro-shaft coupling deformation

由工程力学可知，热流固耦合诱发预成型微型轴热流固耦合变形的驱动力来源于二次成型高温熔体充填流动与微装配界面形成的热流固耦合冲击载荷，主要包括：微装配界面的迎流面与背流面的热流固耦合压力，弹性支撑正应力与侧面黏性拖曳剪切应力。为此揭示微型轴热流固耦合变形的机理应从热流固耦合压力差、弹性支撑正应力与黏性拖曳剪切应力三方面加以分析。现需将微装配界面所承受的热流固耦合压力、黏弹性支撑正应力和黏性拖曳剪切应力的作用进行去耦处理。其微装配界面的热流固耦合载荷工况分为载荷工况1： 受承耦合压力差；载荷工况2：受承耦合压力差和弹性支撑正应力；载荷工况3：受承耦合压力和黏性拖曳剪应力。图5为弹性支撑正应力对耦合变形影响模拟结果，图6为黏性摩擦拖曳剪切应力对耦合变形影响的模拟结果，图7为黏弹性热流固耦合载荷工况与微型轴热流固耦合变形的关联关系。图5和图7的载荷工况1和载荷工况2对比分析结果表明：载荷工况1的微型轴变形明显大于载荷工况2，说明二次成型高温黏弹性熔体充填流动诱导的弹性支撑正应力对微装配界面产生弹性支撑边界约束作用，对变形起抑制作用。图6和图7的载荷工况1和载荷工况3对比分析结果表明：载荷工况1的微型轴变形明显小于载荷工况3的变形，说明二次成型高温黏弹性熔体充填流动诱发的黏性摩擦拖曳剪切应力对微装配界面产生黏性摩擦拖曳边界约束作用，对耦合变形起促进作用。

(a)载荷工况1 (b)载荷工况2图6 黏性拖曳剪切应力对耦合变形影响(η=3267 Pa·s)Fig.6 Influence of viscous friction drag shear stress on micro-shaft coupling deformation

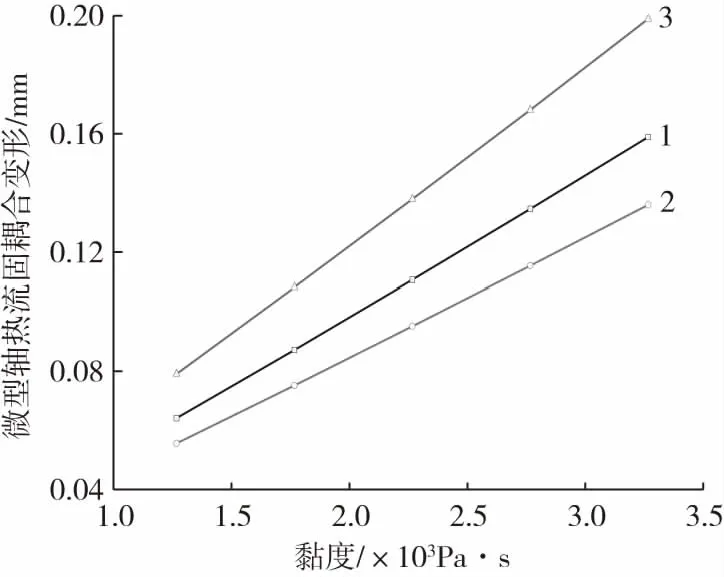
1—载荷工况1 2—载荷工况2 3—载荷工况3图7 黏弹性热流固耦合载荷工况与微型轴变形曲线Fig.7 Viscoelastic thermal-fluid-structure coupling load condition vs. micro-shaft deformation

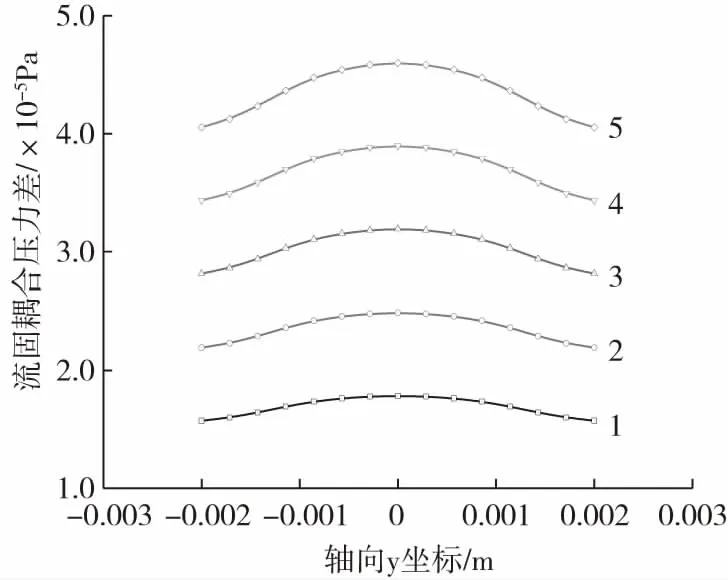
熔体黏度/Pa·s：1—1 267 2—1 767 3—2 267 4—2 767 5—3 267图8 微装配界面所受流固耦合压差与熔体黏度曲线Fig.8 Fluid-structure coupling pressure difference on micro assembly surface vs. melt viscosity

熔体黏度/Pa·s：1—1 267 2—1 767 3—2 267 4—2 767 5—3 267图9 微装配界面所受弹性支撑正应力与黏度曲线Fig.9 Elastic support normal stress on micro assembly surface vs. melt viscosity

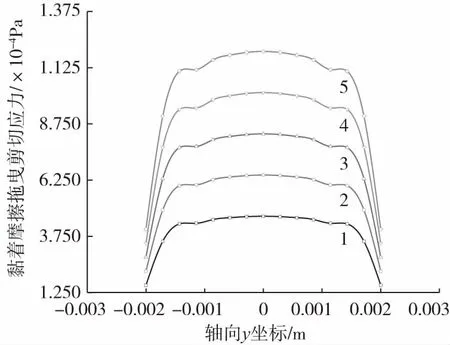
熔体黏度/Pa·s：1—1 267 2—1 767 3—2 267 4—2 767 5—3 267图10 微装配面所受黏着摩擦拖曳剪切应力与黏度曲线Fig.10 Viscous friction drag shear stress on micro assembly surface vs. melt viscosity

为了揭示黏弹性热流固耦合作用诱发热黏弹性变形的机理，本文系统研究了二次成型熔体黏度对微装配面承受的热流固耦合载荷的影响规律。图8、图9和图10分别为二次成型熔体黏度对微装配面所受热流固耦合压力差、弹性支撑正应力和黏性拖曳剪应力影响的模拟结果，研究表明微装配界面沿迎流面与背流面的沿中心线所受耦合压力差、弹性支撑正应力和二侧面所受黏性拖曳剪应力沿轴线均呈抛物线分布，且随着二次成型熔体黏度增大而增加，表明随着二次成型熔体黏性增大，二次成型熔体充模流动与微装配界面的热流固耦合作用增强。微型轴的弯曲变形与微型轴所受的流固耦合压力差和黏性摩擦拖曳剪切应力成正比，而与其所受的弹性支撑应力和弹性模量成反比。当后续成型高温黏弹性熔体的黏度由1 267 Pa·s增大至3 267 Pa·s，微装配界面所受的流固耦合压力差Δp由178 427.2 Pa增大到460 011.9 Pa，增幅为157.8 %；微装配界面所受的黏性摩擦拖曳剪切应力τ13由46 437 Pa增大到119 733.7 Pa，增幅为157.8 %；微装配界面所受的弹性支撑应力τ11由30 891.1 Pa增大到79 652.2 Pa，增幅为157.8 %。由此可见，由于(Δp+τ13-τ11)增大了306 119.9 Pa，微型轴弯曲变形应随二次成型熔体黏度增大而增大。这一推论与图4的微型轴热流固耦合变形随黏度增大而增大的模拟结果完全相吻合，表明本文的理论模型和模拟方法是可靠的。

3 结论

(1)研究建立了综合考虑二次成型黏弹性熔体充填流动约束环境影响的模内微装配成型过程的黏弹性流固耦合变形的机理理论模型；

(2)黏弹性热流固耦合作用诱发的预成型微型轴热流固耦合变形的驱动力来源于二次成型高温熔体充填流动与微装配界面形成的热流固耦合冲击载荷，其主要由热流固耦合压力、弹性支撑正应力和黏性拖曳剪应力构成，黏弹性热流固耦合变形与热流固耦合压力差和黏性拖曳剪应力呈正关联关系，而与弹性支撑正应力呈负关联关系，热流固耦合压力差、弹性支撑正应力和黏性拖曳剪应力均随着二次成型充填流动熔体的黏度增大而增大，表明随着二次成型熔体黏性增大，二次成型熔体充填流动与微装配界面的热流固耦合作用增强；

(3)减小二次成型熔体黏度，可抑制二次成型熔体充填流动与微装配界面的热流固耦合作用，从而导致微装配界面所承受的热流固耦合压力、弹性支撑正应力和黏性拖曳剪应力降低，因而能有效抑制微型轴热流固耦合变形形成，提高模内微装配成型加工的精度。

[1] ANANTHANARAYANAN A, GUPTA S K, BRUCK H A. Characterization of a Reverse Molding Sequence at the Mesoscale for In-mold Assembly of Revolute Joints[J].Polymer Engineering and Science,2010,50(9): 1 843-1 852.

[2] BEJGEROWSKI W. In-Mold Assembly of Multi-Functional Structures[D]. USA: University of Maryland, 2010.

[3] ISLAM A, HANSEN H, Marhöfer M, et al. Two-component Micro Injection Moulding for Hearing Aid Applications[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(5/6/7/8): 605-615.

[4] MICHAELI W, KAMPS T. Micro Assembly Injection Moulding with Plasma Treated Inserts[J]. Microsyst Technol, 2008,14(12):1 903-1 907.

[5] ATTIA U M, HAUATA M, WALTON I, et al. Creating Movable Interfaces by Micro-powder Injection Moul-ding[J]. Journal of Materials Processing Technology, 2014, 214(2): 295-303.

[6] PIOTTER V, PROKOP J, RITZHAUPT H J, et al. Multi-component Microinjection Moulding-trends and Developments[J]. Int J Adv Manuf Technol,2010, 47(1/2/3/4):63-71.

[7] STEVE M, DIETMAR D. Micro Assembly Injection Moulding with variothermal Mould Tempering[J]. Microsystem Technologies, 2017, 23(4):1 017-1 025.

[8] 周国发, 胡 舵, 刘 岑. 剪切变稀效应对微型机械模内组装成型流固耦合变形的影响[J]. 高分子材料科学与工程,2012,28(12): 183-186.

ZHOU G F, HU D, LIU C.Influence of Shear-thinning on Polymer Micromachine Fluid-Solid Coupling Deformation in In-mold Assmbly Molding Process[J]. Polymer Materials Science and Engineering, 2012,28(12): 183-186.

[9] 周国发,王文光,刘 岑. 过程参数对微型机械模内组装成型流固耦合变形影响[J]. 塑性工程学报,2012, 19(1):107-112.

ZHOU G F, WANG W G, LIU C,Influence of Process Parameters on Polymer Micromachine Fluid-solid Coupling Deformation in In-mold Assembly Molding Process[J]. Journal of Plasticity Engineering, 2012, 19(1):107-112.

[10] 周国发，王梅媚，张 宇.聚合物多相分层流动黏弹性包围机制的数值模拟研究[J].复合材料学报, 2014, 31(6): 1 618-1 625.

ZHOU G F, WANG M M, ZANG Y. The Numerical Simulation on the Mechanism of Viscoelastic Encapsulation in Polymer Multiphase Stratified Flows[J].Acta Materiae Compositae Sinica, 2014, 31(6): 1 618-1 625.

[11] RAJAGOPALAN D, ARRMSTRONG R C, BROWN R A. Finite Element Methods for Calculation of Steady Viscoelastic Flow Using Constitutive Equations with a Newtonian Viscosity[J]. Journal of Non-Newtonian Fluid Mechanics, 1990(36): 159-192.

[12] 周文彦,周国发. 聚合物多层气辅共挤精密成型机制的数值分析[J]. 复合材料学报, 2009，26(3):90-98.

ZHOU W Y, ZHOU G F. Numerical Investigation on the Mechanism of Polymer Multilayer Gas Assisted Co-extrusion Precision Molding Process[J]. Acta Materiae Compositae Sinica, 2009, 26(3):90-98.

[13] DIRCKX M E. Demolding of Hot Embossed Polymer Microstructures[D]. USA: Massachusetts Institute of Technology, 2010.