核电站用PE-HD管水压试验压力变化规律研究
秦胤康,施建峰*,侯东圣,郑津洋,郭伟灿
(1.浙江大学化工机械研究所,杭州 310027;2.浙江省特种设备检验研究院,杭州 310020)
0 前言
核电站通常利用海水作为外围冷却回路的冷却剂,但是海水由于盐分和氯离子含量高,腐蚀性很强[1]。PE-HD管道由于优越的耐腐蚀性能,目前已在美国Callaway[2]、中国三门等核电站的冷却水管道系统中应用,其既可以抵抗恶劣使用环境引起的外表面腐蚀,也可以防止流质引起的管内积垢和内表面腐蚀[3-4]。
PE-HD管作为核电站冷却水输送管道,其安全性能备受关注,需从材料、设计、制造、施工检验和无损检测等方面保证其系统安全性。实际使用的PE-HD管通常强度裕量很大,关键需控制制造过程缺陷以及连接后管道系统的严密性。项目组前期利用相控阵超声检测技术已成功实现了三门核电外径762 mm壁厚84.7 mm的核电站用PE-HD管接头内缺陷的无损检测[5-6]。管道连接的严密性方面,水压试验是检验管道严密性的重要手段,为此国内外均制定了水压试验标准用于规范试验流程和验收指标。对比国内外水压试验标准可以发现,虽然水压试验流程各不相同,但均有保压和稳压2个阶段。保压阶段通过不断补水维持管道内压的恒定,稳压阶段不补水以观察压力变化。
PE-HD管材具有黏弹性的特性,管道系统承受内压时,随着时间的增加,材料弹性模量逐渐减小[7],导致管道容积变大,其内部应力应变随之发生变化。该过程介于松弛和蠕变之间,但由于变形量很小,该过程可用松弛过程来描述。由水的状态方程(压力 - 体积 - 温度的关系)可知,当环境温度一定时,水体积变大引起水压变小。因此在PE-HD管承受内压时,即使PE-HD管道无泄漏发生,由于PE-HD管发生应力松弛,管道内压也会不断下降。
项目组前期针对油气输送领域使用的钢丝缠绕增强塑料复合管稳压过程提出了压力变化规律的预测方法,并将理论计算结果与实验结果进行对比,验证了该方法的有效性[8]。但由于管道结构的不同,该方法还不能直接用于核电站用PE-HD管的研究,同时该方法也未考虑管道两端约束类型、保压时间以及温度对压降的影响。本文基于PE-HD管长时力学模型和水的状态方程,提出了一种研究PE-HD管压力变化规律的方法,并讨论了影响管内压力变化规律的因素。
1 理论模型
PE-HD管的状态参数(压力和体积)是管道与水的相互作用结果,任意时刻均处于平衡状态,平衡状态下管道的容积(Vi)、内压(Pi)与水的体积(Vw)、压力(Pw)保持一致。由于黏弹性材料PE-HD的性质,水压试验过程中管道的应力应变会发生变化,管道的容积和内压也会变化,Vi与Pi的关系可用PE-HD管长时力学模型来描述。考虑水的性质,在一定温度下,Vw与Pw的关系可用水的状态方程来描述。因此为了研究水压试验PE-HD管的松弛规律,需描述黏弹性材料PE-HD的应力松弛过程,同时对PE-HD管的长时力学模型和水状态方程进行讨论。
1.1 PE-HD的松弛模量方程
黏弹性材料PE-HD的应力松弛过程可以通过模量方程E(t)来表征,通过模量方程可计算出任一时刻下PE-HD的模量。松弛模量数据可以通过试验获得,大多数材料的应力松弛模量可以用扩展指数型经验公式来表达[9-10],如式(1):
(1)
式中E0——初始模量,MPa
E∞——长期模量,MPa
t——载荷作用时间,h
β、τ——参数,其中0<β<1,τ>0
松弛模量方程确定后,任意时刻PE-HD的模量可知。
PE-HD的模量还与环境温度有关,因此在实际的工程应用中,还需考虑温度对水压试验压降的影响。基于不同温度下的聚乙烯的模量数据[11],拟合出考虑温度影响的PE-HD的松弛模量方程,如式(2):
E(t,T)= (-4.88T+563.58)+(808.26-20.75T+
(2)
式中T——PE-HD管道壁温, ℃
基于该方程可作出不同温度下的PE-HD模量随时间变化曲线,如图1所示。可以看出随着温度的增加,PE-HD的模量不断减小,模量变化率也逐渐减小。
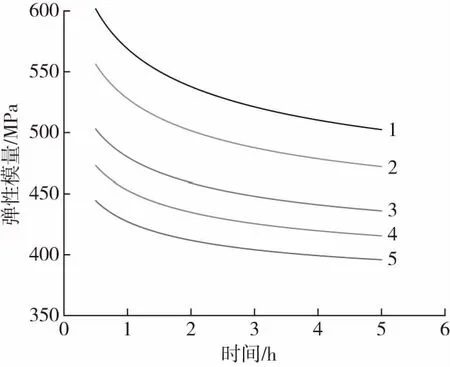
温度/℃:1—23 2—27 3—32 4—35 5—38图1 不同温度下的PE-HD模量随时间变化曲线Fig.1 Modulus of PE-HD at different temperatures
1.2 管道长时力学模型
PE-HD管道长时力学模型用来描述Vi与Pi的关系,为求解PE-HD管道的容积Vi,需要已知管道的结构参数、载荷参数、材料性能和端部约束。在内压Pi作用下,外径Do[内半径(a)、外半径(b)]、壁厚(δ)、长度(l)的PE-HD管道的简化模型如图2所示。管道的长度远大于管道直径,可以认为在离两端足够远处的应力和应变分布沿管道长度方向没有差异。管道的材料性能包括弹性模量和泊松比(v),其中PE-HD任一时刻的模量可通过式(2)计算,泊松比v通常取0.45。管道端部约束介于自由和固定之间,考虑理想情况,分别在端部自由和端部固定约束下,讨论管道Vi与Pi的关系[12]。
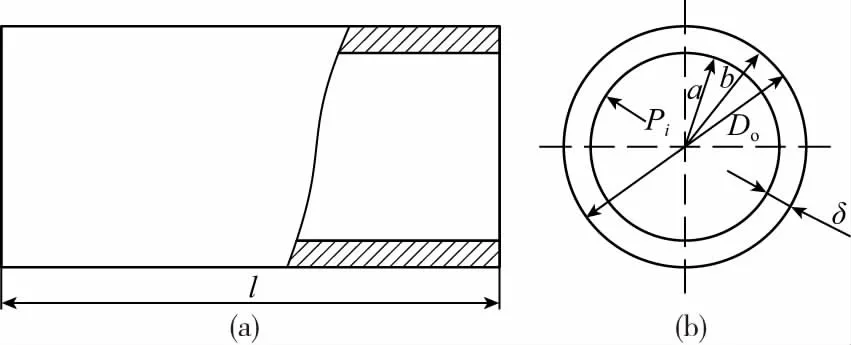
(a)剖视图 (b)截面图图2 PE-HD管简化模型Fig.2 Simplified model of PE-HD pipes
由管道的结构参数,可求出管道的容积Vi:
Vi=πa2l(1+εθ)2(1+εz)
(3)
其中,εθ、εz分别为管道的环向应变和轴向应变(ε),由广义胡克定律得:
(4)
在端部自由条件下,管道内壁处的应力(σ)可表示为:
(5)
将式(5)代入式(4)可求得管道的环向应变和轴向应变的表达式:
⟺APi
(6)

(7)
式中G——材料的切变模量,G=E/[2(1+v)]
则系数A、B可表示为:
(8)
在端部固定条件下,管道内壁处的σθ和σr与端部自由条件下的相同,但轴向应变εz=0,由以上条件可求得管道的环向应变的表达式:
⟺CPi
(9)
则系数C可表示为:
(10)
综上所述,在端部自由和端部固定两种理想条件下,PE-HD管道容积和内压的关系如表1所示,其中A、B、C均是与管道材料和结构有关的系数。

表1 端部自由和端部固定时PE-HD管的Vi-Pi方程Tab.1 Vi-Pi of PE-HD pipes under different types of constraint (free ends and fixed ends)
1.3 水的状态方程
PE-HD松弛模量随时间不断变化,管道从一个平衡状态转变成另一个平衡状态,水的状态也因此发生改变。现已有许多经验公式可以表征水的压力、体积与温度之间的关系[13],最简单有效的是Tumlirz方程,如式(11)所示,其适用范围为:水的温度在0~40 ℃,水压小于300 MPa[14],P0、v0、λ0为关于温度(T,℃)的函数。
(11)
式中Pw——水压(表压),MPa
vw——比体积,mL/g
Vw——水的体积,mL
M——水的质量,g
基于Kennedy水的压力 - 体积 - 温度原始数据[14],拟合出Tumlirz方程中各参数,得到水的状态方程式(12):
=177.950+1.125T-0.007 45T2
(12)
2 平衡状态点的确定
在水压试验过程中,任意时刻PE-HD的模量确定后,都有一定的压力和体积。此压力和体积是该时刻下管道力学性能曲线Vi-Pi与该温度下水状态曲线Vw-Pw交点处的压力和体积,该点称为平衡状态点。显然,该点所代表的压力和体积既满足管道力学平衡的要求,又满足水的状态方程。通过对平衡状态点进行分析可得到PE-HD管水压试验的容积和压力变化。
保压阶段压力P已知,由式(3)可求得保压结束时刻管道的容积V,然后由式(12)可求得方程中关键参数M;稳压阶段水的质量M已知,联立式(3)和式(12)可求得任一时刻的管道内压力P和容积V。据此分析得出各阶段的状态点变化如图3所示。保压阶段对应平衡状态点1向平衡状态点2的变化过程;稳压阶段对应平衡状态点2向平衡状态点3的变化过程。
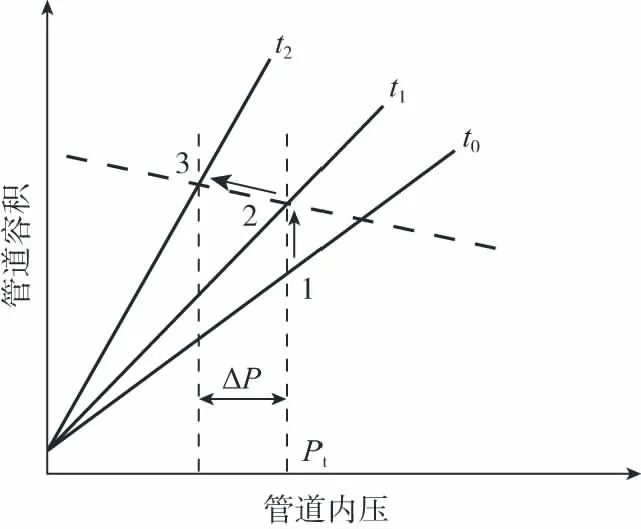
—Vi-Pi —Vw-Pw图3 平衡状态点变化示意图Fig.3 Transformation of the balanced state
3 结果分析与讨论
应用上述方法研究PE-HD管道水压试验松弛规律,由于本文研究对象为核电站PE-HD管道,所以相关结构和载荷参数取自ASME Code Case N-755中的引用标准ASTM F714-13[15],根据计算结果分别讨论管道端部约束、保压时间和温度对压力变化的影响。通常试验过程管道端部不均匀变形部分很小,分析过程可忽略管道端部的影响。
3.1 管道端部约束
通过不同的约束类型会计算得到不同的Vi-Pi方程,从而影响水压试验的压降和压降速率。以管道外径548.64 mm的不同壁厚的PE-HD管为例,不同约束类型下压降计算结果如表2所示。
从表2可以看出,在PE-HD管端部自由和端部固定2种约束类型下,计算得到的压降基本一致,因此约束类型对PE-HD管水压试验压力变化影响较小。进一步分析,由式(4)可以看出,由于材料的泊松比v接近0.5,管道端部自由时,环向应力和径向应力引起的轴向收缩与轴向应力引起的轴向拉伸相抵消,轴向应变εz接近于零,而管道端部固定时,管道轴向应变εz为零;对比式(8)和式(10)可以看出,系数A和系数C基本相同,因此端部自由和端部固定两种约束类型下计算得到的压降基本一致。实际投入使用的PE-HD管道端部约束往往介于自由和固定之间,且偏向于端部固定,因此后文压降采用端部固定约束进行计算。
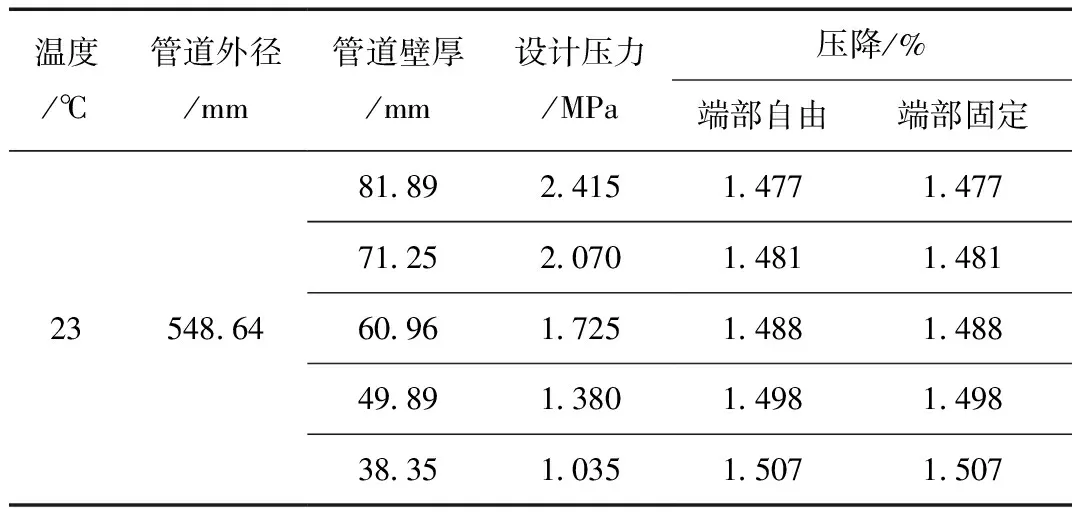
表2 不同约束类型下PE-HD管压降计算结果Tab.2 Pressure drop of PE-HD pipes under different types of constraint
3.2 保压时间
国内外均有相关标准规定了聚乙烯管道水压试验流程及验收指标,通过对比可以发现,试验流程均包含保压和稳压两个阶段,但不同标准规定的保压时间不尽相同,验收指标多采用稳压阶段的压降作为参考依据。常温下,设置保压时间分别为1、2、3、4 h,观察不同保压时间对稳压阶段压降及压力变化的影响,结果如表3和图4所示。
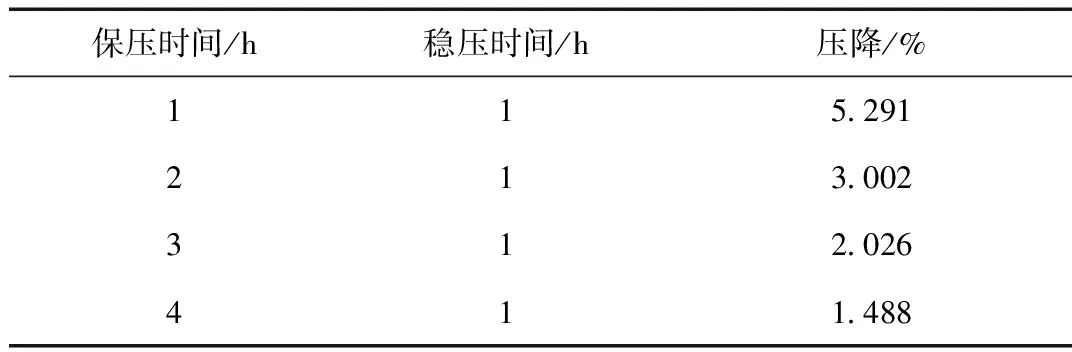
表3 不同保压时间下PE-HD管稳压阶段压降Tab.3 Pressure drop of PE-HD pipes with different pressure holding time
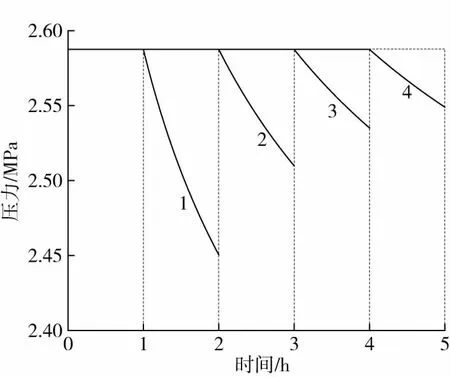
保压时间/h:1—1 2—2 3—3 4—4图4 不同保压时间下PE-HD管压力随时间变化曲线Fig.4 Pressure change of PE-HD pipes with time with different pressure holding time
从表3和图4可以看出,随着保压时间的增加,压降明显降低,压降速率也变慢。进一步分析,结合图1可以看出,随着时间的增加,PE-HD的模量逐渐减小,模量变化率也逐渐降低。保压阶段可以让管道完成初始膨胀,度过材料模量变化较快的时间区域。随着保压时间的增加,稳压阶段材料模量变化减小,因此压降和压降速率均降低,压力变化趋于稳定。
3.3 温度
PE-HD管水压试验都是在现场进行的,保压期间环境温度可能发生变化,因此还需要考虑温度对平衡状态点的影响。温度升高会使PE-HD模量变小,导致变形增大,同时温度升高,会导致水体积膨胀,两者相互作用共同引起压降的变化。
以管道外径548.64 mm、管道壁厚60.96 mm的PE-HD管为例,研究温度对压降的影响,保压4 h,稳压1 h,温度设置分别为23、27、32、35、38 ℃,得到压降随温度变化曲线如图5所示,不同温度下的压力变化规律如图6所示。
从图5可以看出,随着温度的增加,压降逐渐减小,且压降与温度大致呈线性关系。从图6可以看出,当温度一定时,稳压阶段的PE-HD管道存在明显的压降,且下降速率先快后慢。由于环境温度同时影响PE-HD材料性能和水的状态方程,为研究温度对两者的影响,分别改变壁温和水温为23、27、32、35、38 ℃,得到的结果如表4所示。
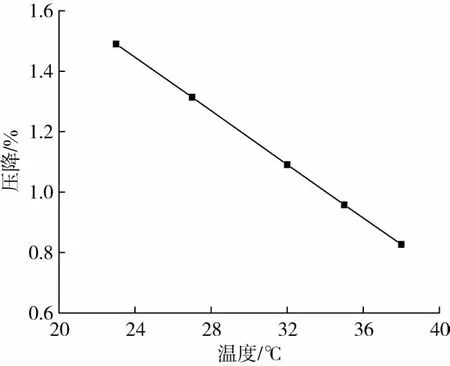
图5 压降随温度变化关系曲线Fig.5 Pressure decline of PE-HD pipes with time
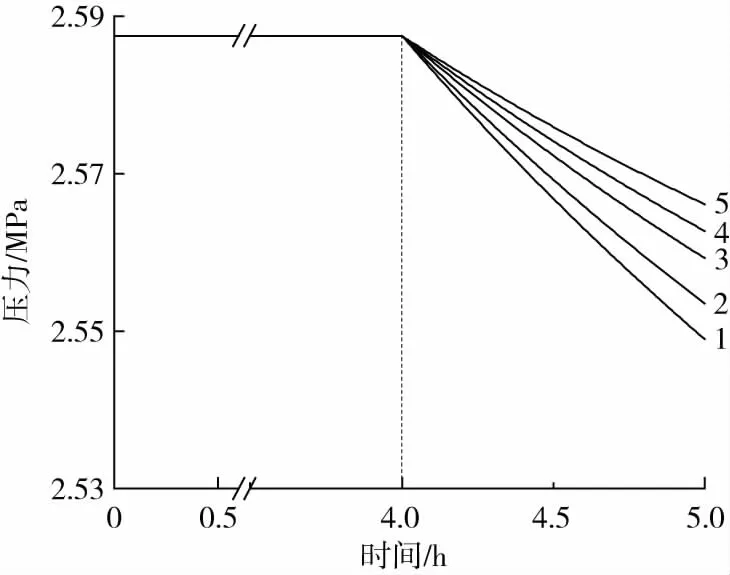
温度/℃:1—23 2—27 3—32 4—35 5—38图6 不同温度下压力随时间变化曲线Fig.6 Pressure change of PE-HD pipes with time at different temperatures
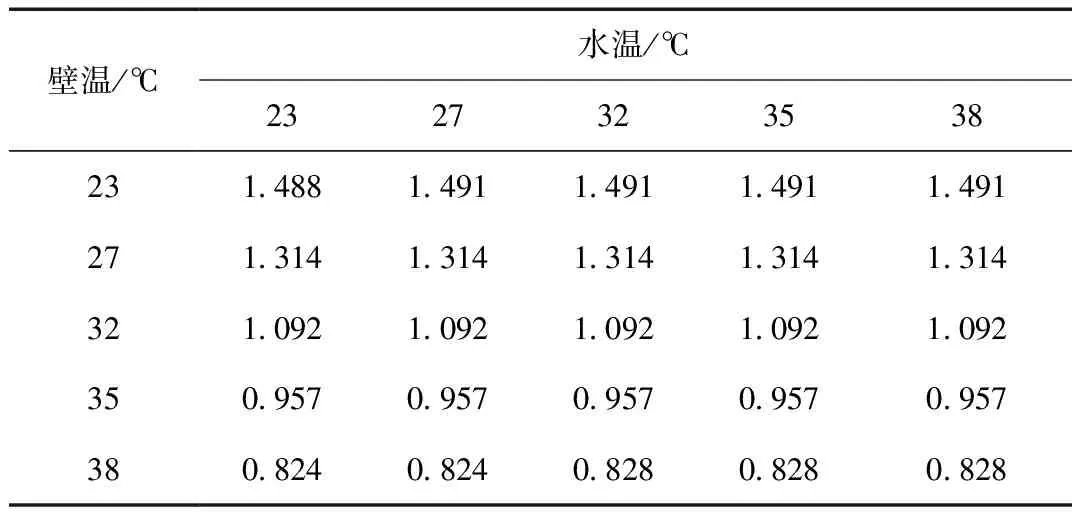
表4 不同壁温和水温下PE-HD管稳压阶段的压降 %Tab.4 Pressure decline of PE-HD pipes under different temperature of walls or water %
从表4可以看出,一定壁温下,水的温度的改变对压降的影响极小。从图7可以看出,壁温一定,各时刻下的Vi-Pi曲线恒定不变。而温度和稳压阶段水的质量M同时改变,导致水的状态曲线由T1转变为T2,对应稳压阶段结束状态点3向3′的变化,压降略有增加,但变化较小。
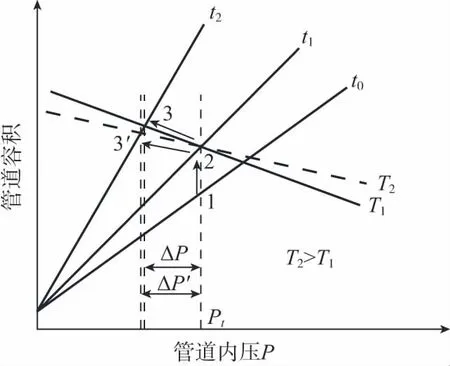
图7 水温变化对压降的影响Fig.7 Effect of water temperature change on pressure decline
而一定水温下,壁温的改变对压降的影响较大,从表4中可以看出,随着壁温的增加,压降不断减小。进一步分析,从图8可以看出,温度减小导致模量增加,稳压阶段初末时刻的Vi-Pi曲线发生变化,由温度T1转化为温度T2时的状态。而壁温一定,水状态方程仅与稳压阶段水的质量M有关。稳压阶段压力变化过程由温度T1时状态点2→3变化为温度T2时状态点2′→3′。
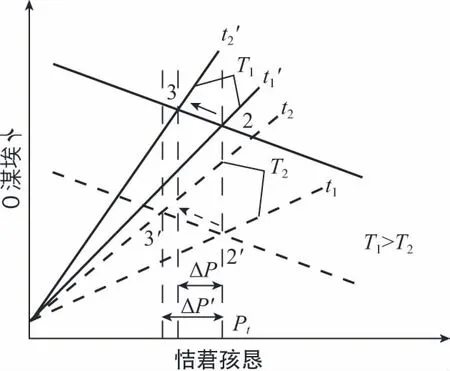
图8 壁温变化对压降的影响Fig.8 Effect of wall temperature change on pressure drop
在实际水压试验时,经过4 h的保压后,管道壁温和水温基本相同。当壁温和水温同时发生变化时,壁温变化的影响起主要作用,随着温度的增加,压降明显降低。
3.4 松弛模量的合理性验证
在水压试验过程中,PE-HD管道产生变形,应力、应变均随时间变化,该过程介于蠕变和松弛之间。由于管道变形量很小,该过程可近似利用松弛过程来描述。基于此,本文利用松弛模量方程来表征PE-HD的黏弹性,因此需对松弛模量的合理性进行验证。
基于上述方法,可以求得PE-HD管内壁环向应力、应变,如图9所示。稳压阶段,管道内壁环向应变由0.019 41变为0.019 42,上升0.052 %;管道内壁环向应力由10.55 MPa下降到10.39 MPa,下降了1.5 %。在考虑整个过程PE-HD的力学性质随时间变化时,可以认为环向应变保持在0.019 4水平不变,应力不断下降,即近似认为PE-HD在稳压过程发生了应力松弛。
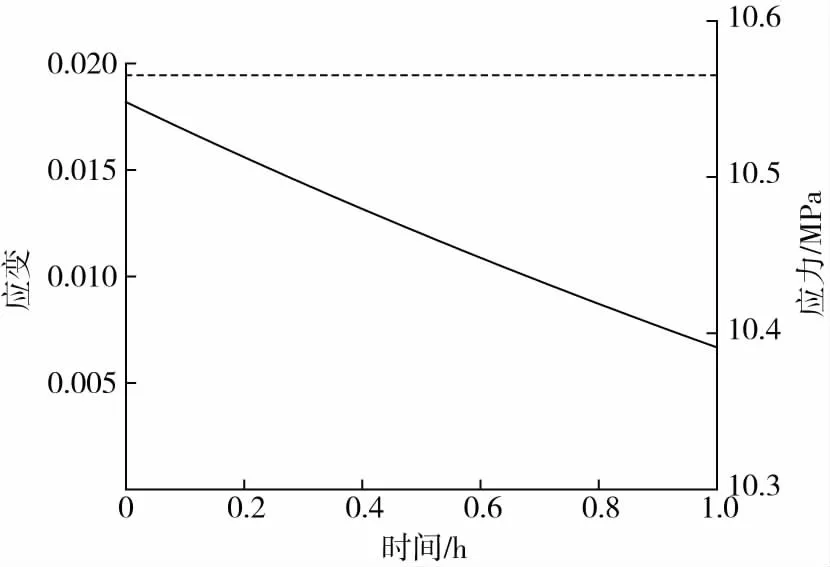
—应力 —应变图9 稳压阶段PE-HD管内壁环向应力 - 应变曲线Fig.9 Hoop stress and hoop strain change with time in inner surface of PE-HD pipes
4 结论
(1)对于水压试验常用的端部自由和端部固定两种约束方法,由于材料泊松比接近于0.5,环向应力和径向应力引起的轴向收缩与轴向应力引起的轴向拉伸相抵消,轴向应变εz接近于零,2种约束类型对压降的影响不超过0.1 %;
(2)保压时间对水压试验压降和压降速率有很大的影响,保压时间增加,水压试验压降和压降速率均下降,有助于提高试验的稳定性;
(3)水温和壁温对压降的影响趋势相反,水温增加导致压降增加,壁温增加导致压降减小;水温对压降的影响小,壁温的影响起主要作用;随着温度的增加,PE-HD管水压试验稳压阶段的压降减小,温度和压降大致呈线性关系。
[1] 刘飞华,任 爱,杨 帆,等. 核电站海水冷却系统的腐蚀与防腐蚀设计[J]. 腐蚀与防护,2007, 28(6): 313-316.
LIU F H, REN A, YANG F, et al. Corrosion and Protection Design of Seawater Cooling System in NPP[J]. Corrosion and Protection,2007, 28(6): 313-316.
[2] ABEL S L, BRANDES M D, Corley L J, et al. Use of HDPE Piping in the Callaway Nuclear Plant Essential Service Water System[C]//ASME 2009 Pressure Vessels and Piping Conference. 2009:1 285-1 293.
[3] FREDERICK C, PORTER A, ZIMMERMAN D. High-Density Polyethylene Piping Butt-fusion Joint Examination Using Ultrasonic Phased Array[J]. Journal of Pressure Vessel Technology,2010, 132(5): 51 501.
[4] 王立娟,王焱鹏,马 丽,等. 管材用高密度聚乙烯树脂研究进展[J]. 中国塑料,2014,28(2): 1-5.
WANG L J, WANG Y P, MA L, et al. Research Progress in High Density Polyethylene Resin for Plastics Pipe[J]. China Plastics,2014,28(2): 1-5.
[5] ZHENG J Y, HOU D S, GUO W C, et al. Ultrasonic Inspection of Electrofusion Joints of Large Polyethylene Pipes in Nuclear Power Plants[J]. Journal of Pressure Vessel Technology, 2016,138(12): 060908.
[6] 王 非,李广忠,卲汉增,等. 聚乙烯管道接头超声检测基础数据库软件开发[J]. 中国塑料,2010,26(6): 86-90.
WANG F, LI G Z, SHAO H Z, et al. Development of Ultrasonic Detection Database of Polyethylene Pipe Joints[J]. China Plastics,2010,26(6): 86-90.
[7] KHELIF R, CHATEAUNEUF A, CHAOUI K. Reliability-based Assessment of Polyethylene Pipe Creep Lifetime[J]. International Journal of Pressure Vessels and Piping,2007, 84(12): 697-707.
[8] ZHENG J, HOU D, ZHONG S, et al. Effect of Viscoelasticity on the Hold Pressure of Plastic Pipe Reinforced by Cross Helically Wound Steel Wires in Leak Test[J]. Composite Structures,2015(133): 756-763.
[9] 张为民. 松弛模量与蠕变柔量的实用表达式[J]. 湘潭大学自然科学学报,1999(3): 26-28.
ZHANG W M. Practical Expressions of Relaxation Modulus and Creep Compliance[J]. Journal of Xiangtan University Natural Science,1999(3): 26-28.
[10] 陈锦裕,朱志彬,杨晓翔. PE80燃气管道的应力松弛模型与实验验证[J]. 中国塑料,2016,30(4): 93-98.
CHEN J Y, ZHU Z B, YANG X X. Viscoelasticity Mechanics Model of Medium Density Polythylene Pipes[J]. China Plastics,2016,30(4): 93-98.
[11] POPELAR C F, POPELAR C H, KENNER V H. Viscoelastic Material Characterization and Modeling for Polyethylene[J]. Polymer Engineering & Science,1990, 30(10): 577-586.
[12] 郑津洋,桑芝富. 过程设备设计[M]. 北京:化学工业出版社, 2015:39-42.
[13] Macdonald J R. Review of Some Experimental and Analytical Equations of State[J]. Reviews of Modern Phy-sics,1969, 41(2): 316.
[14] Eckart C H. The Equation of State of Water and Sea Water at Low Temperatures and Pressures, Part 2 of Pro-perties of Water[J]. American Journal of Science,1958, 256(4): 225-240.
[15] ASTM International. F714-13 Standard Specification for Polyethylene (PE) Plastic Pipe (DR-PR) Based on Outside Diameter[S]. PA: ASTM, 2013.

