基于改进差分进化算法的地下水污染溶质运移时空模拟研究

田金凤

(辽宁省本溪水文局，辽宁 本溪 117000)

对于地下水污染物溶质运移规律的研究和分析有助于对区域地下水污染物进行有效防治和保护，然而地下水污染物溶质运移影响要素较多，多呈现非线性变化影响，为此对于地下水污染物溶质运移规律分析一直是个难点。近些年来，许多学者结合数学解析方法或数学模型的方式对地下水污染物溶质运移的规律进行模拟分析，取得一定研究成果[1- 6]，但这些成果大都集中于对地下水污染物溶质时间过程规律的分析模拟，而对地下水污染物溶质运移时空模拟分析的研究较少。当前，也有学者提出地下水污染物溶质运移的二维模拟方程，并结合数学差分方法对方程进行了求解[7- 9]，但传统差分算法不能调整差分网格的优化计算策略，不能求得优化解，为此有学者对传统差分算法进行改进，引入适度函数对差分网格的优化计算策略进行逐步进化调整，确保取得方程的优化解。本文引入改进的差分求解算法对地下水污染溶质运移的方程进行求解，并以辽宁东部为研究实例，对比分析不同算法对方程求解精度的影响。

1 基于改进差分进化算法的地下水污染溶质运移计算原理

本文采用二维地下水污染物运移方程对地下水污染物溶质运移进行模拟计算，并结合改进的非结构差分方法对方程进行求解，地下水污染物二维运移方程首先需要对地下水水流流动方向进行模拟，计算方程为：

(1)

式中，Kxx—水平方向的渗透系数，LT-1；Kyy—垂直方向的渗透系数，LT-1；h—计算时地下水水头，L；w—单位体积内地下水出流量，L-1；Ss—地下水蓄水系数。

在描述地下水水流方程后，进行地下水污染物溶质运移方程，计算方程为：

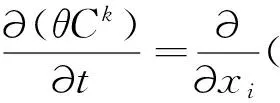
(2)

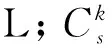
在式(2)中化学反应项可以表述为下列方程：

(3)

对于特征污染物浓度CL-溶质运移计算方程为：

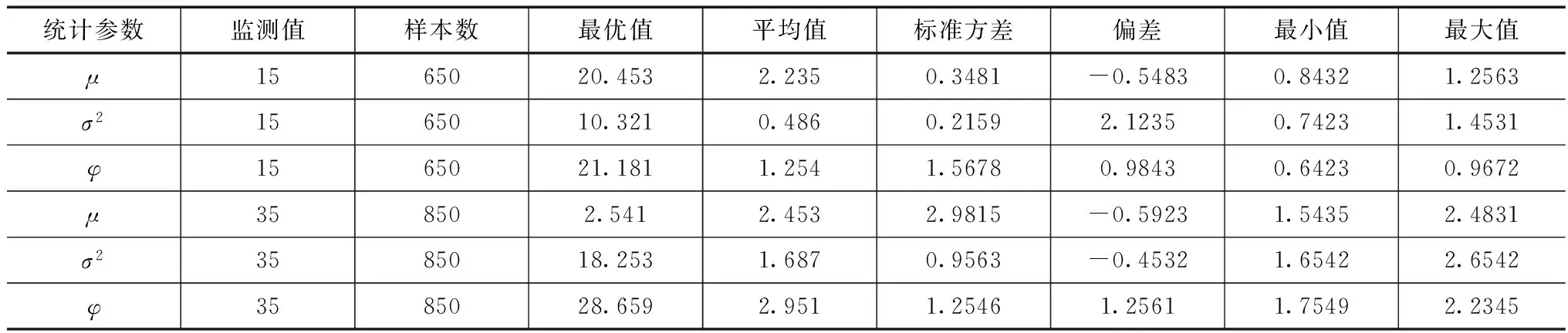
表1 模型统计参数后验分布结果

注：标准参数不是模型的计算参数，而是模型样本序列的统计参数。

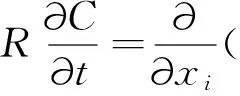
(4)

式中，qs′—瞬态地下水污染运移的速率，LT-1，其他变量含义同式(3)中变量的含义。

其中，式(3)有两个定解计算条件，分别为：

C(x，y，t)|t=0=C0(x，y)

(5)

C(x，y，t)|t=0=C1(x，y)

(6)

式中，R—地下水污染物溶质运移延迟系数；C0—污染物浓度初值，ML-3；C1(x，y)—上边界条件下的污染物浓度函数。

本文采用改进的差分进化算法对地下水污染物溶质运移的二维方程进行差分求解，改进差分进化算法演绎不用新的计算网格单元来对差分进行进化演算，演算方程为：

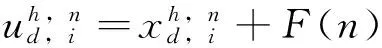
(7)

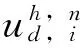
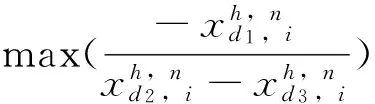
(8)

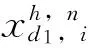
结合改进的差分进化算法对地下水污染物溶质运移的二维方程进行逐单元网格进化演算，实现区域地下水污染物溶质运移的时空分布模拟。

2 模型应用

2.1 区域概况

本文以辽宁东部为研究实例，该区域具有长期的地下水污染物监测数据，并且监测点较多，研究区域的面积为105km2，区域地下水污染物最大浓度均值为0.039mg/L。结合该区域的地下水监测数据，结合不同算法对区域地下水溶度运移进行时空分布的模拟分析。

2.2 模型参数检验

为分析模型进行检验，结合区域内监测点样本数据，对模型进行统计参数后验分布，统计参数后验分布结果见表1，此外对模型不同百分位计算标准值进行了检验，检验结果见表2。

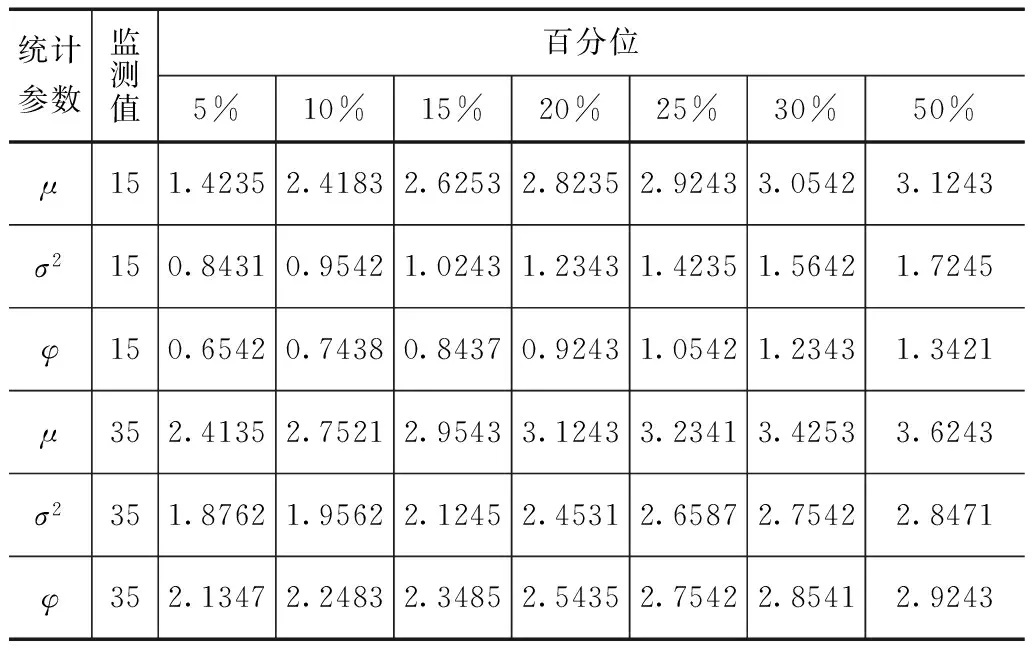
表2 模型不同百分位计算统计参数检验结果

由表1可知，模型统计参数后验分布均不服从均匀分布，地下水污染物溶质运移方程的统计参数随着样本数据的增多，呈现较为明显的振荡变化，模型方程收敛速度逐步加快，统计参数φ较其他参数在模型计算初期有着较为明显的振荡变化现象。模型统计参数后验分布集中度逐步增加而统计标准误差逐步减小，有助于模型寻优求解。由表2可知，当方程百分位点据增加后，方程统计参数值逐步较大，参数置信区间进一步得到扩充。

2.3 渗透系数变动下地下水污染物溶质运移不确定性试验分析

考虑渗透系数变化对地下水污染溶质运移的不确定性影响，结合数据试验方式定量分析了变渗透系数对地下水污染物溶质运移的不确定性影响。分析结果见表3。

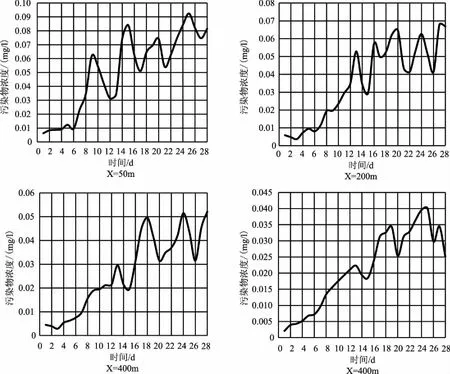
图1 基于改进差分进化算法的地下水污染物溶质运移浓度变化过程

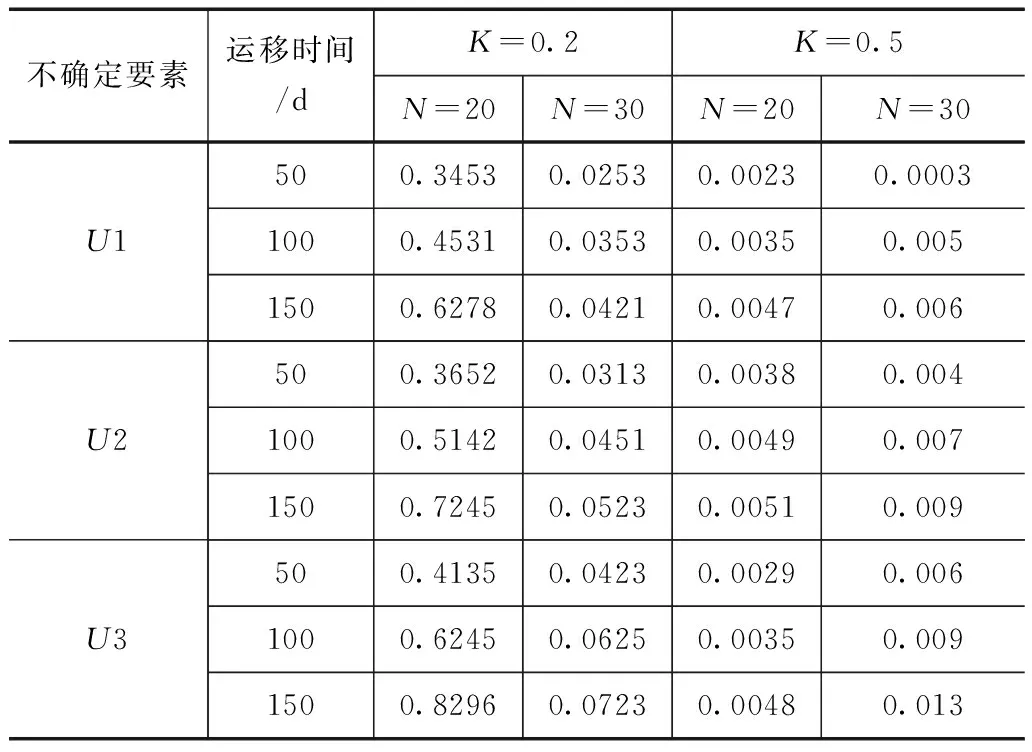
表3 地下水污染物溶质运移不确定试验分析结果

由表3可知，随着地下水污染物溶质运移时间的增加，各渗透系数下随着样本数据系列的增多而污染物溶质运移的不确定性也逐步增加，从表中还可以看出，在相同渗透系数条件下不同确定要素类型对地下水污染物溶质运移影响较小，但渗透系数非均匀性对地下水污染物溶质运移不确定性影响却较为明显。随着运移时间的增加，模型参数不确定性相比于随机模拟不确定要素对方程溶质运移影响较大，为此在进行地下水污染溶质运移模拟时，需要对模型参数的不确定性进行综合考虑。

2.4 地下水污染溶质运移时间过程模拟研究

为对比不同算法对方程求解精度影响，结合区域监测污染运移数据，对比分析了不同算法对方程求解精度的影响，分析结果见表4及图1。

由表4可知，相比于传统差分算法，改进的差分算法对地下水污染物溶质运移方程求解精度有着较为明显的改善，以地下水污染物溶质运移最大浓度误差而言，相比于传统算法，改进的差分进化算法计算误差均值减少14.4%，且不同运移时间和运用距离的最大浓度计算误差都小于传统算法。从图1中可以看出，随着运移距离的增加，地下水污染物溶质浓度逐步降低，可见随着地下水运用距离增加，地下水污染物溶度影响范围也逐步缩小。

表4 不同方法预测地下水污染物溶质运移最大浓度计算对比结果

2.5 地下水污染溶质运移空间分布模拟研究

为分析地下水污染溶质运移空间分布的规律，结合改进差分进化算法对地下水污染物溶质运移方程进行了求解，并以区域上下边界监测的污染物浓度作为边界条件，模拟分析了不同运移时间下地下水污染物浓度的空间分布，结果见图2。

图2 不同运移时间的地下水污染物浓度空间分布模拟结果

从图2中可以看出，随着运移时间的增加，区域地下水污染物浓度低值区域增加，地下水污染物浓度高值区域逐步减少，且呈现由中部有外部逐步弥散的趋势，这主要是地下水污染物随着地下水水流流动，且浓度逐步向外弥散，而在浓度弥散的过程中，地下水污染物的浓度逐步减少。区域中上部地下水污染物高浓度区域随着运移时间推移变化较为缓慢，这主要和区域地形有关，该部分区域地形地势较低，污染物运移较为困难，因此浓度变化较小，可见地下水污染物溶质运移浓度分布不仅受地下水水流流动影响，还受到地形影响。

3 结论

本文结合改进差分算法对地下水污染物溶质运移方程进行求解，实现了辽宁东部某区域地下水污染物溶质运移时空分布的模拟，分析取得以下结论。

(1)采用改进差分算法后，地下水污染物溶质运移方程统计参数随着样本数据的增多，呈现较为明显的振荡变化，模型收敛和寻求速度逐步加快，相比于传统算法，改进算法在，地下水污染物溶质运移模拟精度得到明显改善。

(2)随着运移距离增加，地下水污染物浓度沿程逐步降低；受地下水流弥散作用，随着运移时间增加，区域地下水污染物浓度高值区减少，低值区逐步增多，但地形对地下水污染物浓度分布影响也较大。

[1] 金云龙, 邱锦安, 刘远锋, 等. 地下水污染物运移数值模拟研究及应用综述[J]. 地下水, 2016(03): 21- 23.

[2] 秦鹏飞. 多类型垃圾场地污染地下水风险综合评估[J]. 水利技术监督, 2017(03): 19- 22.

[3] 谢文逸. 基于GMS的某电厂地下水污染物运移研究[D]. 合肥工业大学, 2013.

[4] 米热古丽·麦麦提. 地下水污染现状调查及处理[J]. 水利规划与设计, 2013(11): 35- 37.

[5] 尉鹏翔. Visual Modflow在地下水污染物运移模拟中的应用[J]. 水资源保护, 2011(04): 19- 21+41.

[6] 安秉锋. 沈阳市地下水反应运移特性分析[J]. 水利技术监督, 2017(01): 63- 65+145.

[7] 吴亚楠. 多孔介质溶质运移机理实验研究[D]. 合肥工业大学, 2015.

[8] 胡海珠. 河湖防渗条件下包气带再生水反应运移及其对地下水环境影响研究[D]. 中国农业大学, 2014.

[9] 李华, 吴静, 徐世光, 等. 基于GMS的云南德厚水库下游废弃砒霜厂地下水溶质运移模拟[J]. 水资源与水工程学报, 2014(02): 209- 212+217.