一种快速测试多孔介质声学特征参数的方法

王永华，武海权，刘哲明，玛丽-安妮克加郎，于化东

（1.长春理工大学 机电工程学院，长春 130022；2.里昂中央理工大学 实验流体力学和声学合作实验室，法国 69131）

噪声对人类日常生活的影响越来越重。生活中方方面面都在被噪声干扰。因此，对于噪声的减弱与防止就显得尤为重要。最常用便捷的方法有两种，一种是改变噪声的传播途径，另一种是用吸声材料对噪声进行吸收。吸声材料在生活中随处可见，如建筑、交通、军事、航空领域。它的发展不仅关系着人民生活的环境，与国家军事力量也息息相关。

开孔泡沫作为最常用的吸声多孔材料，其声学性能主要依赖其固有特征。因此，为了达到多孔材料的按需优化以及为特定场合筛选合适的多孔材料的目的，多孔材料特征参数的研究就非常重要。其主要测试方法如下：

流阻的测试主要有直接测试法和比较分析法。直接测量法需要测量厚度为e的多孔材料两侧的压力差ΔP和流体的流速或体积流量u，通过流体的阻力R定义为R=ΔP/u，流阻σ=R/e。比较分析法需要将两个多孔材料串联放置，第一个材料作为参考样本，其对空气的阻力R1已知（可从精确理论模型或现有的直接测量法获得），根据流量恒定，可由参考样本的压降ΔP1和测试样本的测试值ΔP2得到所求阻力R2的值，进而求得流阻。

孔隙率可通过Beranek设计的装置测得。Champoux等提出了一种相似的方法，用电子传感器来精确测量压力，提高了测量精度。其工作原理是通过活塞的压力变化来推导材料孔内的饱和空气体积Vf，应用Boyle-Mariotte定律得到样本中空气体积后，由Φ=Vf/Vt计算孔隙率。

目前，曲率可基于多孔材料内部倾斜的超声波和各种不同入射角度的反射波测量，该方法快速、无损，并可同时获得孔隙率。图1为该方法的原理图，其中P.G为脉冲发射器，H.F.F-P.A为前置放大器和高频滤波器，D.O为数字示波器，C为纵坐标。曲率由以下方程确定：

其中，θ1和θ2为入射角；r1和r2分别为对应入射角的反射系数。

图1 Fellah等确定孔隙率和曲率的方法

黏性特征长度和热特征长度可通过低频的超声波测量同时得到。

以上可看出多孔介质中的声传播需要多个特征参数来表征。Johnson-Allard模型包含5个特征参数，Lafarge-Allard模型有6个参数，这些参数需要分别用不同的设备测试出来，过程繁琐复杂。本文基于多孔材料刚骨架模型Johnson-Allard[1］和Lafarge-Allard[2］模型，设计了一个试验台，该试验台可以同时测定所有的参数。本文首先介绍了多孔介质的理论传播模型、测试原理和搭建的试验台，然后通过对毛毡的各个特征参数的测试过程来介绍测试条件和方法，最后评价测试方法的可靠性。

1 试验原理

（1）理论模型

在声学计算中，通常引入ρe(ω)ejωt来表示单色平面波。可以将多孔介质看成一个虚构的等效流体，那么有效密度和压缩量K(ω)与频率有关[3］。多孔介质中的压力和声速由Helmholtz方程获得：

引入两相介质中的传播常数k(ω)和特征常数Zc(ω)，则：

从上式可看出，多孔介质中的声传播可以通过这两种方法确定，一种是有效密度和动态压缩（ρe，K），另一种是特征阻抗和传播常数（Zc，k）确定。

（2）测试原理

本测试方法的基本原理是多孔材料吸声系数测试的阻抗管法[4］，主声源发出声波，声波通过样本表面，再通过麦克风收集管内声压，估算材料的表面阻抗，这样，本文根据其声传播模型来推导其特征参数，原理示意图见图2。

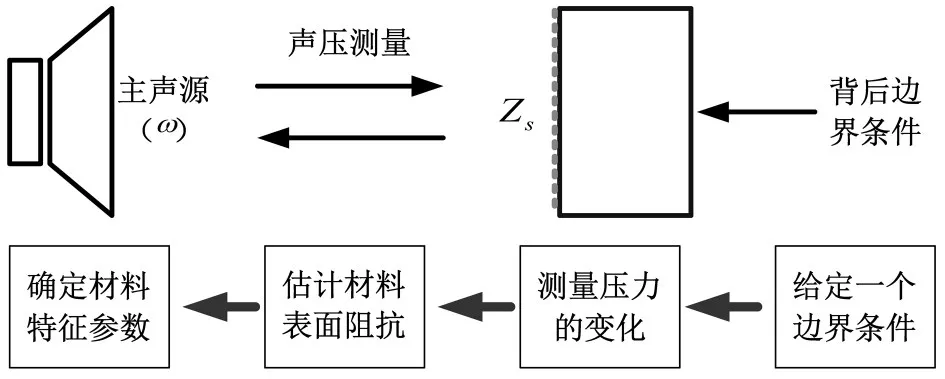
图2 多孔材料特征参数测试原理示意图

当条件为低频，并且多孔材料背后为软边界时，其表面阻抗Zs的实部与流阻σ成正比：

在低频率，背后压力为0的条件下，由下式测试样本的表面阻抗，流阻σ可以确定为：

孔隙率Φ可由基于Lafarge-Allard模型的低频渐进近似法来求得。由于样本的二阶表面导纳受到限制，当频率趋于0时：

背后为刚性壁的多孔材料的表面导纳的求孔隙率就可以求出来：

在Johnson-Allard模型中，有效密度ρe和动态压缩K可以用流阻σ，孔隙率Φ，曲率α∞，热特征常数Λ和粘性特征常数Λ'来表达。黏性效应和惯性[5］为：

在Lafarge-Allard模型中引入了一个参数热渗透性k0'[6］，相比于Johnson-Allard模型，对低频范围的刚性骨架与孔之间的热交换的描述更加精确。k0'是由类似Darcy定律中的黏性渗透性来定义的，可以用多孔材料的诱捕常数Γ来表示：

通过以上方法，可以得到流阻σ和孔隙率Φ的值。在Johnson-Allard模型中，其他三个参数α∞，s，s'的确定则是采用MATLAB编程，采用最小二乘法，将Johnson-Allard模型与测试的样本的表面阻抗（或吸声系数）试验曲线拟合获得。而对于Lafarge-Allard模型，则可以同时确定α∞、Λ、Λ'和k0'。由于四个参数的最小二乘法计算时间长，且优化结果不理想，所以可将其分为（α∞，Λ）和（Λ'，k0'）两组。有效密度仅取决于α∞和Λ，动态压缩包括Λ'和k0'，故可以采用最小二乘法，基于有效密度和动态压缩的拟合求解确定四个参数。

2 测试方法

（1）试验台搭建

本试验设备的主体是横截面为55×55mm2的驻波管，可测试频段50～2500Hz，如图3所示。将主声源放置在驻波管的一侧，驻波管发出的平面波从管内向另一侧的多孔介质传播，在材料后面放置一个金属推杆装置，它的主要作用是用来改变多孔介质背后的边界条件。在管道中心放置一金属杆，金属杆前端连接一个传感器，金属杆可以在管道径向方向移动。测流阻时主声源发出30～300Hz的交变信号，测其他参数时，声源产生50～2500Hz的正弦信号。材料背后的边界条件可以为刚性壁、不同厚度的空气层和软阻抗等，如图4所示。

图3 设计的快速测试试验台

图4 材料背后不同的边界条件

（2）参数测试

①驻波管内声速c0

其中，γ为理想气体常数，这种方法仅仅依赖于环境温度。

②表面阻抗和吸声系数

设阻抗管内两个麦克风之间的距离为s，通过麦克风之间传递函数h12推导材料的表面声阻抗，然后计算垂直入射的反射系数，进而求得吸声系数。

其中，Z0为空气的特征阻抗，l为麦克风1到材料表面的距离。对比研究发现采用一个麦克风在不同位置测试结果最准确。为确定多孔材料整个频段的表面阻抗，采用插值法，麦克风间距为0.15m时测试低频50～500Hz的值，0.1m时测中间频段500～700Hz，0.2m时测高频段700～2500Hz，插值图如图5所示，α1为低频段，α2为中间频段，α3为高频段，可对测量的表面阻抗值在全频段进行整合。

图5 吸声系数和表面阻抗的插值函数

图6 Utsuno法测试特征阻抗和传播常数原理图

③有效密度和动态压缩

有效密度和动态压缩可由特征阻抗Zc和传递常数k确定，而Zc和k可通过Utsuno法测量多孔材料背衬刚性壁和60mm空气层的表面阻抗值来确定，示意图如图6所示。

其中，Zs1和Zs2分别为多孔材料背衬刚性壁和60mm空气层的表面阻抗测量值，Za1和Za2分别为相同条件下计算得到的材料背后的阻抗值，e为材料厚度。对于i=1，2，式14和15可写为：

特征阻抗和传播常数可表示为：

选择正的特征阻抗的实部，为避免两个测量区域太近的阻抗间产生不确定性，d1和d2须满足条件fΔd=f(d2-d1)＜c0/2。当最高频率为2500Hz时，满足条件。最后，由Zc和k的试验值推导ρe，K为：

3 测试过程

选择厚度为0.025m的毛毡多孔样本来阐述整个特征参数确定方法。

（1）流阻

当材料骨架为弹性时，阻抗的实部不会立刻达到渐进值σe[8］，此时前面介绍的流阻的确定原理是不适用的。故需要根据流阻的定义式来确定流阻值。本文设计了一个可以控制多孔材料背后的压力并且使之为零的主动控制系统。通过测得多孔材料表面阻抗的方法来计算流阻，主要是筛选出阻抗的实部并用其接近常数的频率范围，进而算出平均值即为所求。图7所示为背压P=0条件下的毛毡的表面阻抗值，得到流阻为23150rayls/m。

图7 背压P=0时低频表面阻抗及流阻确定（Re为实部，Im为虚部）

（2）孔隙率

毛毡样本对频率的解Φs如图8所示。需要选择固定振幅的均方差最小的频段间隔（至少40Hz）来求解方程6的解，孔隙率的值，即该频段的平均值。通过连续测量证明孔隙率的值，即图中通过计算，在所选择间距内的平均值0.93，证明该方法的可重复性。

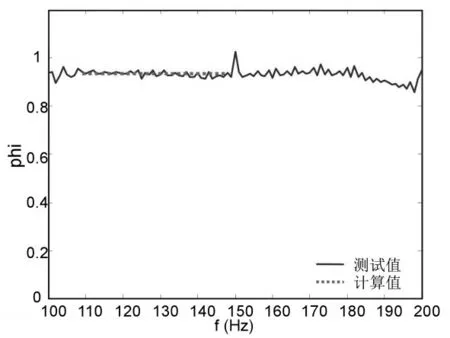
图8 孔隙率求解

（3）曲率和形状因子

选择60mm空气层的背后条件，通过吸声系数的拟合优化，得到α∞=1.1，s=0.5，s'=1.4（图9）。进而求得 Λ=4.34×105m ，Λ'=1.21×10-4m 。预测结果与试验结果吻合良好。

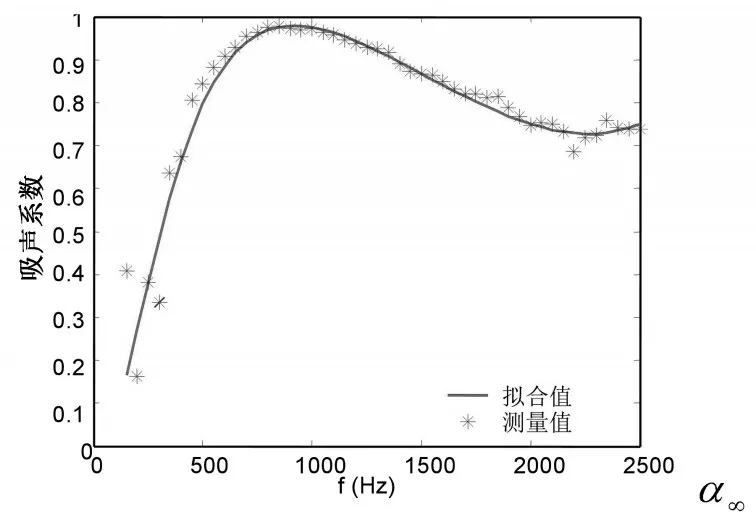
图9 背衬60mm空气层吸声系数的拟合

（4）曲率和特征长度

基于Lafarge-Allard模型，采用Utsuno法确定特征阻抗和传递常数[9］。在50～2500Hz范围内，选择背衬刚性壁和60mm空腔的条件，经过与有效密度拟合优化，得到α∞=1，Λ=3.6×10-5m，s=0.44（图10a）。经过与动态压缩拟合求解得到Λ'=1.78×10-4m ，k0'=3.7×10-9，s'=2.15，M'=1（图10b）。

图10 通过有效密度和动态压缩进行拟合求解（Re为实部，Im为虚部）

（5）测试方法验证

根据上述得到的参数值，可计算得到其他条件（这里选择120mm空气层）下的吸声系数和阻抗曲线，与测试得到的值相比较，如图11所示，证明该方法是否有效的标准是预测值与试验值是否吻合，从图中可以看出，预测值与实验值比较吻合，该方法是有效的。

图11 背衬120mm空气层下吸声系数和阻抗试验值与预测值比较

4 结论

本文设计了一个自制声学装置，能够基于声学测试，可以同时测试多孔介质中声传播的所有特征参数，解决了传统测试耗时，昂贵且需要大量专业设备的缺点。基于Johnson-Allard和Lafarge-Allard两种理论模型，确定流阻、孔隙率、曲率、黏性特征长度、热特征长度和热渗透6个物理参数，该方法有效且具有良好的准确性。

[1]孙少明，任露泉，徐成宇.长耳鸮皮肤和覆羽耦合吸声降噪特性研究[J］.噪声与振动控制，2008，28（3）：119-123.

[2]孙少明.风机气动噪声控制耦合仿生研究[D］.吉林：吉林大学博士论文，2008.

[3]孙敏，张倩索，张荣，等.前置放大器的低噪声设计[J］.长春理工大学学报：自然科学版，2011，34（2）：51-53.

[4]弯艳玲，李守魁，李元宝.附加质量块对某型轿车车内噪声影响的试验研究[J］.长春理工大学学报：自然科学版，2013，36（6）：82-85.

[5]Iain D.J.Dupère，卢天健，Ann P.Dowling.声学多孔材料的孔结构优化[J］.西安交通大学学报，2007，（11）：1251-1256.

[6]王建忠，汤慧萍，敖庆波，等.金属纤维多孔材料复合结构的声学性能[J］.中国材料进展，2017，36（Z1）：550-556，565.

[7]王星博.多孔材料元胞自动机声学建模及高声压激励下材料的声学性能研究[D］.银川：宁夏大学，2016.

[8]王亚南.含多孔层和不同材料层的复合隔墙板的隔声探究[D］.南昌：南昌航空大学，2015.

[9]孙文娟，苏巧平，刘丽.微穿孔板吸声体混合结构的声学性能研究[J］.世界科技研究与发展，2016，38（06）：1165-1169.