一题多解在不定积分中的应用

孟献青

（山西大同大学数学与计算机科学学院,山西大同 037009）

一题多解教学是启发和引导学生从不同的角度，用不同的方法解决同一数学问题的教学形式。一题多解可以帮助学生提高对高等数学的学习兴趣，帮助学生深刻理解定理内在的意义，增强学生对各个方法之间的联系，培养学生从不同角度，不同方面学以致用，使乏味的高等数学活灵活现。下面以求解不定积分为例，充分体现一题多解在高等数学中的作用。

1 理论依据[1]

不定积分的计算必须具有扎实且丰富的基础知识。常用的计算不定积分的方法有基本积分公式，不定积分的第一类换元法和第二类换元法，分部积分法，有理函数的积分。第一类换元法主要是凑微分法和代数换元法，第二类换元法主要是三角换元法。另外在做题过程中，也可以结合加项减项法，三角函数的恒等变形等简化计算。对于不定积分的计算，方法比较多，而且也比较灵活，只有通过较多的练习，才能将各种方法熟练地结合起来，才能更快更好的计算不定积分。

2 应用举例[2-3]

例1计算不定积分

首先，考虑用第一类换元法求解，于是有

解1（凑微分法）

解4（代数换元法）

解5（三角换元法）

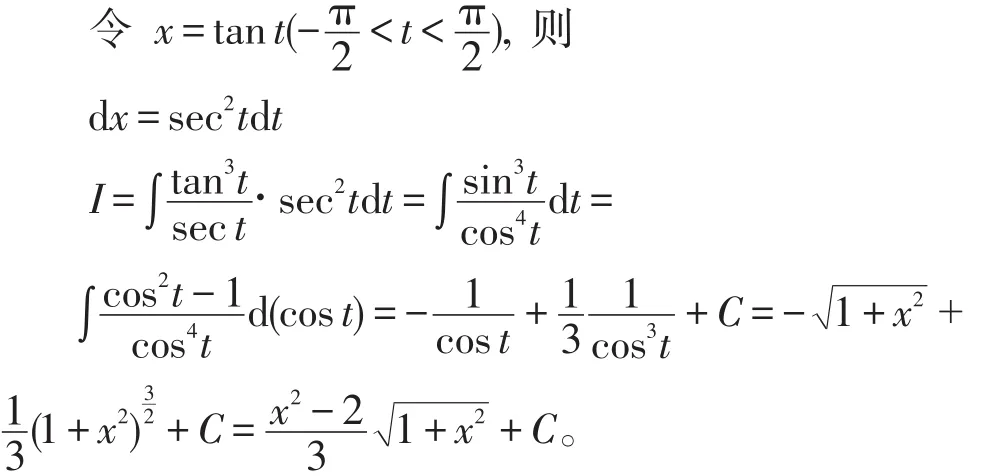
另外，也可以考虑把第一类换元法和分部积分法结合起来进行计算。由解2知，于是

解6（分部积分法）

解7(综合法)

解1（凑微分法）

解2（分部积分法）

解3（换元积分法）

解1（凑微分法）

解3（换元法）令x=t，则x=t2，dx=2tdt

解 4（换元法）令 4-x=t，则x=4-t2，dx=-2tdt，

解5（换元法）令x=2+t，则dx=dt，

解3到解5都是先用换元法，然后再凑微分，但是解5的方法比较巧妙。

解6（三角换元法）

3 结束语[4]

通过一题多解的训练，不仅可以激发学生的学习兴趣，而且还可以开拓他们的解题思路，把学过的知识和方法融会贯通起来。在一题多解的教学过程中，学生的解题思路、方法有机会在其他同学面前展现，这不仅能获得教师的认可，而且还可以增加学生的成就感，这样学生就能更加积极主动地参与到课程的学习中，而不是被动地接受，于是这种积极的心态就能极大地增强学生学好数学的信心，所以一题多解是培养学生发散思维，提高数学兴趣的一种有效教学手段。

[1]同济大学数学系.高等数学(第七版)[M].北京:高等教育出版社,2014.

[2]孟献青,高晓燕.关于曲线积分计算的探讨[J].山西大同大学学报(自然科学版),2017,33（6）：12-13.

[3]龚友运.从不定积分的一题多解浅析高等数学的发散思维[J].教育教学论坛,2011（6）：73-75.

[4]周后卿.积分中的一题多解与思维训练[J].广西教育学院学报,2014(2):158-160.