相邻基坑对拉锚索支护结构参数敏感性分析

吴曙光，韩培宇，宋 康，彭 朋

(1.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045； 2.重庆大学 土木工程学院, 重庆 400045；3.苏州高新景枫投资发展有限公司，江苏 苏州 215010； 4. 长江勘测规划设计研究有限责任公司，湖北 武汉430010)

随着我国城市建设不断深化，高层建筑和超限超高层建筑不断涌现，深基坑工程也越来越密集，不可避免地遇到相邻深基坑等问题。在某些情况下，相邻深基坑之间的坡体由于特殊原因无法进行开挖，且其距离较短，一般桩锚支护结构无法对其进行有效支护。为满足基坑支护要求，就必须考虑桩支护与其他支护相结合的方式。对拉锚固技术是提供一种在满足2个基坑间小净距情况下，可保证支护结构本身安全，保证周围建(构)筑物安全和正常使用的支护方式[1]。

目前，已有学者对对拉锚固结构做了一些有意义的研究工作。欧阳仲春[2]采用弹性土压力来计算拉杆的拉力，并根据弹性理论推导出弹性土压力的表达式；康景文等[3]提出了此种结构破坏状态的一个判别标准和基于此判别标准的一种新设计计算方法；张宏博等[4]设计了室内模型试验，监测并分析了对拉式挡土墙在倾覆破坏和沉降破坏时墙背侧向土压力分布特征及拉筋应力变化规律。对拉锚固技术在桥台加固、桥侧墙加固、隧道加固等方面有较多的应用和研究，但在基坑工程中，特别是结合桩的对拉锚索支护结构则需要进一步研究。

笔者以某一采用桩-对拉锚索支护形式的基坑工程为例，在充分考虑锚索竖向间距、桩直径、相邻基坑间距、锚索预应力、桩间距、桩嵌固段长度等6个因素对桩-对拉锚索支护结构性能影响基础上，利用FLAC3D软件进行支护参数敏感性分析。

1 工程概况

某工程总建筑面积13.8×104m2，地上建筑面积约8.7×104m2，包含2栋高层办公楼，商业裙楼以及相关用房。按设计标高整平场地，在地下室四周将形成高度约20 m基坑边坡。在其基坑东侧与相邻项目的基坑坡后土体地表下约2～5 m范围内埋设有电力管涵和给排水管道。两项目基坑间距约为15 m，基坑间有重庆市江北区主供电电缆箱涵通过，关系到整个江北区的供电和供水问题，坡体不能挖掘。且一旦边坡稳定性不能得到有效保障，整个江北区供电供水将会受到影响。因此必须采取有效的支护形式以确保在基坑施工过程中的安全。若对相邻近距离基坑进行分别单独设置锚索，则会造成其锚索长度过长或者锚固段无法满足要求的情况。

设计采用桩+对拉锚索的支护结构来保证坡体稳定性以及控制变形。基坑支护竖桩为直径1.5 m圆桩，桩中心距为3 m，混凝土强度为C30，锚索竖向间距为2.5 m。采用两侧锚索对拉方案：锚孔直径为180 mm，17根直径为15.2 mm的无黏结预应力锚索。支护结构剖面如图1。土的物理力学性质如表1。

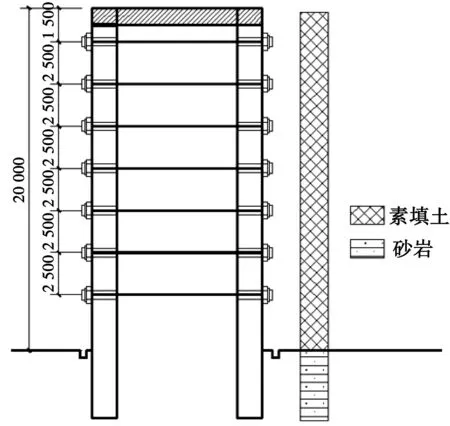
图1 支护结构示意Fig. 1 Sketch of supporting structure

参 数土体名称素填土中风化砂岩黏聚力/kPa302157内摩擦角/(°)20．043．6容重/(kN·m-3)21．324．8变形模量/MPa233932

2 FLAC3D数值模拟

2.1 模型建立

为简化计算，模型宽度方向(Y轴)取两倍桩间距；一般可取下截断边界至坑底的距离为最终开挖深度的3～4倍[5-7]，基坑深度20 m，因此模型高(Z轴)取80 m；长度方向(X轴)考虑基坑开挖影响，两侧各取70 m，即X轴取140 m与相邻基坑间距之和。土体本构模型选用Mohr-Coulombr模型，弹性-理想塑性模型计算结果要好于线弹性模型，适合一般岩土力学分析，如边坡稳定、地下开挖[5]。预应力锚杆采用FLAC3D中的Cable单元，桩采用Pile单元，锚索和桩单元连接采用删除-建立Link的办法建立[8]。由于采用无黏结预应力锚索，所以Cable单元的gr_coh、gr_fric和gr_k均取0，其他参数按工程概况中实际采取方案取值。Pile单元参数分别如表2[9-12]。计算分析的整体思路为：首先完成初始应力场平衡，然后开挖，再进行桩、锚杆等施工。FLAC3D数值计算模型见图2。

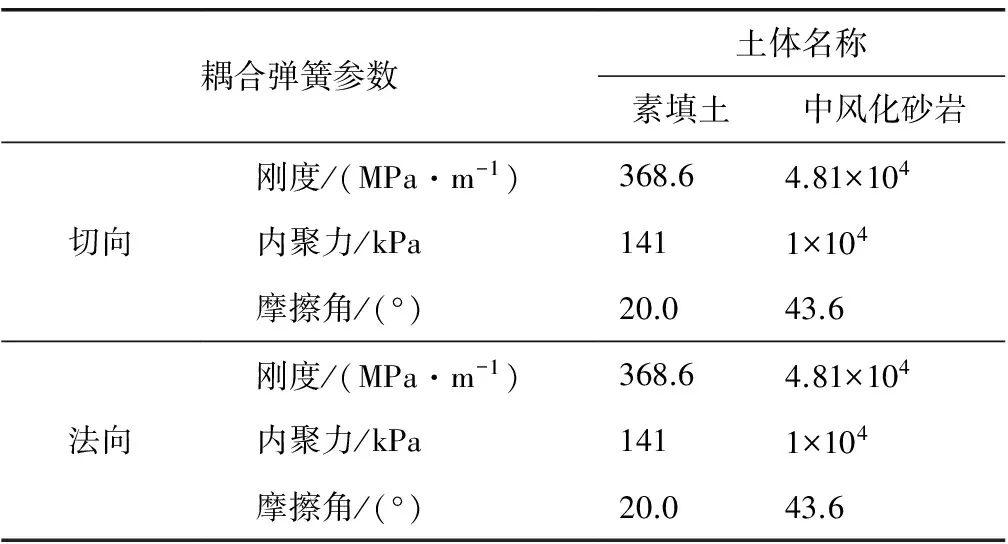
表2 桩单元参数Table 2 Parameters for pile unit

图2 FLAC3D数值计算模型Fig. 2 Numerical calculation model of FLAC3D

由于模型较多，为优化计算，笔者采用参数化建模的思想，设置6个核心参数，即笔者关注的6个影响因素。其他参数，如惯性矩、截面积、周长等通过FLAC3D自动计算。因此每次计算只需改变核心参数，可节约时间与精力。

2.2 分析方案

笔者考虑锚索竖向间距(因素A)、桩直径(因素B)、相邻基坑间距(因素C)、锚索预应力(因素D)、桩间距(因素E)、桩嵌固段长度(因素F)这6个因素对桩-对拉锚索支护结构性能的影响，具体为桩身弯矩、锚索轴力、桩后土体位移等3方面。选定一种方案为基本方案，每次改变一个参数取值。基本方案为锚索竖向间距2.5 m、桩直径1.5 m、桩间距3 m、锚索预应力500 kN、相邻基坑间距15 m、桩嵌固段长度7 m。各参数的取值见表3。

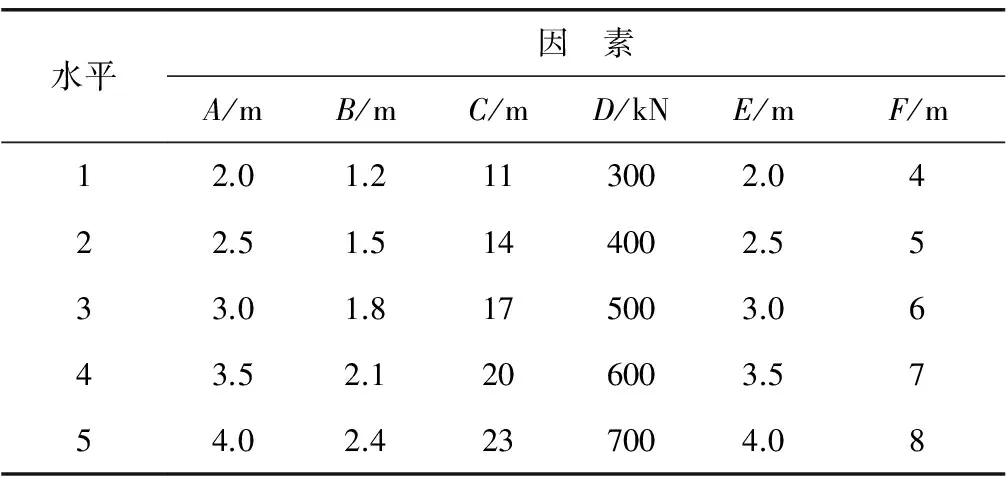
表3 影响因素和水平Table 3 Influence factors and levels

3 结果及分析

3.1 锚索竖向间距对性能的影响

保持其他参数同2.2节中所述基本方案一致，仅调整锚索间距，建立锚索间距为2.0、2.5、3.0、3.5、4.0 m这 5种工况下的计算模型，分别获得沿桩深度方向的桩身弯矩、锚索轴力、桩后土体水平位移(X方向位移，下同)变化曲线(图3)。

由图3(a)可知：桩身弯矩呈“波浪形”，锚索间距越大，起伏越大。波峰点即为锚索位置，这意味着在锚索作用下，桩身弯矩局部减小，锚索起到了控制弯矩的作用；计算中还发现：锚索面积越大，弯矩曲线呈“波浪形”这一特点也越明显。锚索竖向间距由2 m增大到4 m，桩身最大弯矩由1 498 kN·m增长为2 967 kN·m，增长值1 469 kN·m，最大弯矩值为2 m时的1.98倍。

由图3(b)可知：锚索轴力的最大值出现在下部的锚索当中。锚索竖向间距由2 m增大到4 m，锚索最大轴力由597 kN增长为815 kN，增长值218 kN，最大轴力为2 m时的1.36倍。

由图3(c)可知：桩顶后土体位移并不是偏向基坑一侧，而是出现反向位移。出现这种现象的原因是：一方面是预应力存在引起的；另一方面也与对拉锚索远端固定在桩上，而不是锚固在土体当中有关，这种支护形式大大增强了锚索锚固能力。随着锚索间距增大，上部桩后土体位移变小，下部桩后土体位移变大。桩后最大土体位移在接近基坑中下部最大，然后快速减小。增大锚索间距，位移变大，但增大的量有所减小。

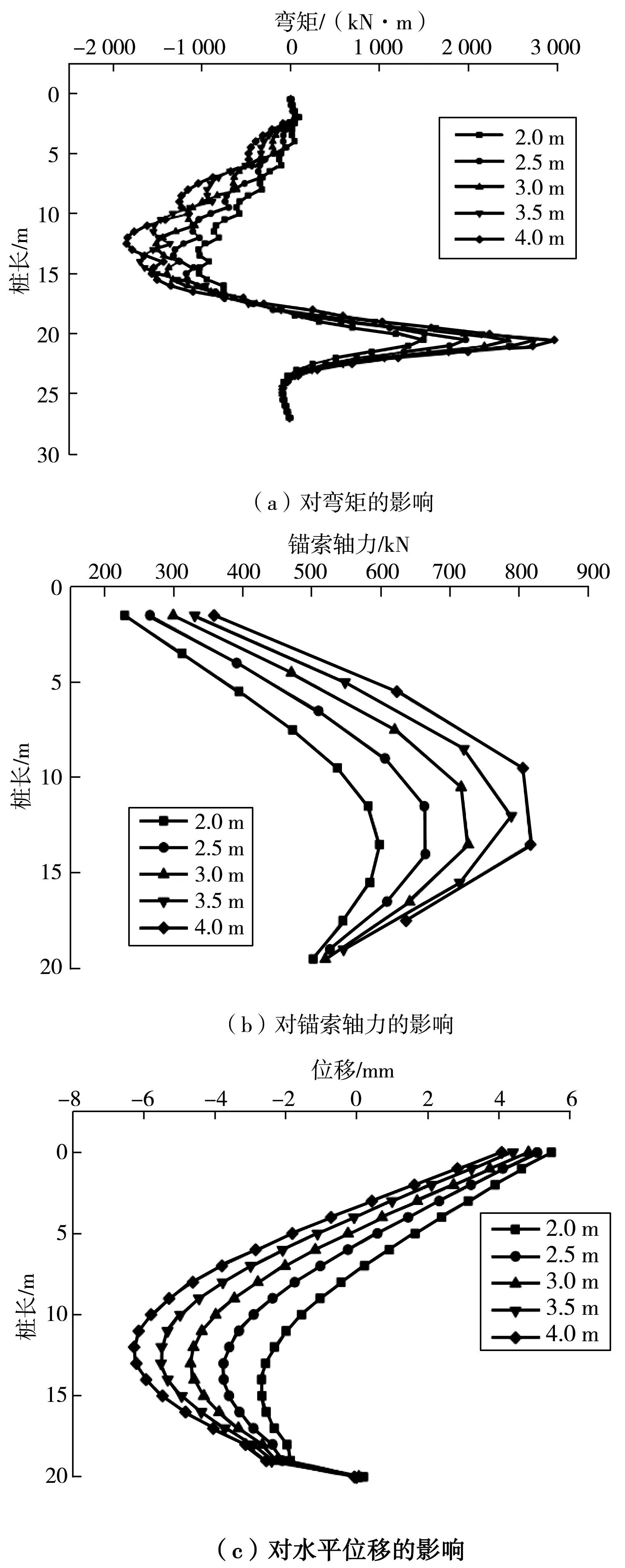
图3 锚索间距对性能的影响Fig. 3 Influence of the spacing of anchor cables on performance

3.2 桩直径对性能的影响

保持其他参数同2.2节中所述基本方案一致，仅调整桩直径，建立直径为1.2、1.5、1.8、2.1、2.4 m这5种工况下的计算模型，分别获得沿桩深度方向的桩身弯矩、锚索轴力、桩后土体水平位移变化曲线(图4)。

由图4(a)可知：桩身弯矩仍然呈现出“波浪形”，但随着桩直径的增大、桩身抗弯能力的提高，这一特点逐渐变弱，锚索局部减小弯矩的作用被弱化。另外可看出：随着桩直径增大，嵌固段弯矩“零点”从22.5 m处逐渐转移到25 m处，即桩的有效抗弯长度随着桩径增大而变长，因此桩嵌固长度的选择要充分考虑桩径影响。桩直径由1.2 m增大到2.4 m，桩身最大弯矩由1 272 kN·m增长为2 754 kN·m，增长值1 482 kN·m，最大弯矩值为1.2 m时的2.16倍。

由图4(b)可知：锚索轴力并没有呈现类似图4中整体变大或变小的趋势。随着桩直径增大，上部锚索轴力变大，下部锚索轴力变小，各排锚索轴力分布因桩直径的增大而变得更加“均匀”，即不同锚索间轴力差值变小，有利于充分发挥材料性能。桩直径由1.2 m增大到2.4 m，锚索最大轴力由702 kN减小为545 kN，减小值为157 kN，最大轴力为1.2 m时的0.78倍。

由图4(c)可知：桩后土体位移变化规律较图5有所变化。随着桩直径增大，上部桩后土体位移变小，下部桩后土体位移也变小，桩后土体位移分布更加“均匀”。当桩直径小于1.5m时，桩后土体位移没有得到有效控制，建议桩径不小于1.5 m。

3.3 相邻基坑间距对性能的影响

保持其他参数同2.2节中所述基本方案一致，仅调整相邻基坑间距，建立间距为11、14、17、20、23 m这5种工况下的计算模型，分别获得沿桩深度方向的桩身弯矩、锚索轴力、桩后土体水平位移变化曲线(图5)。

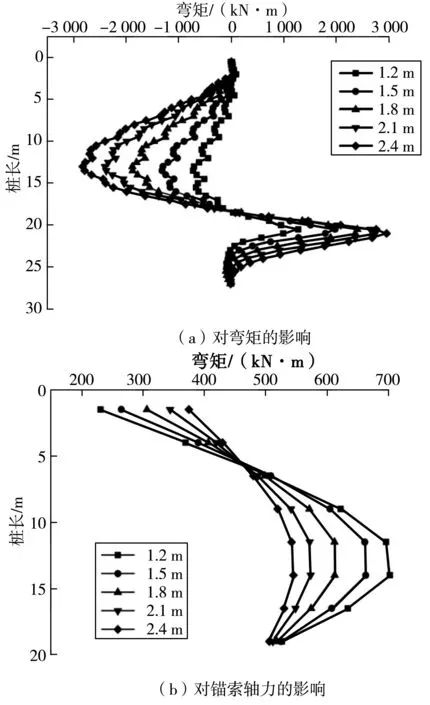
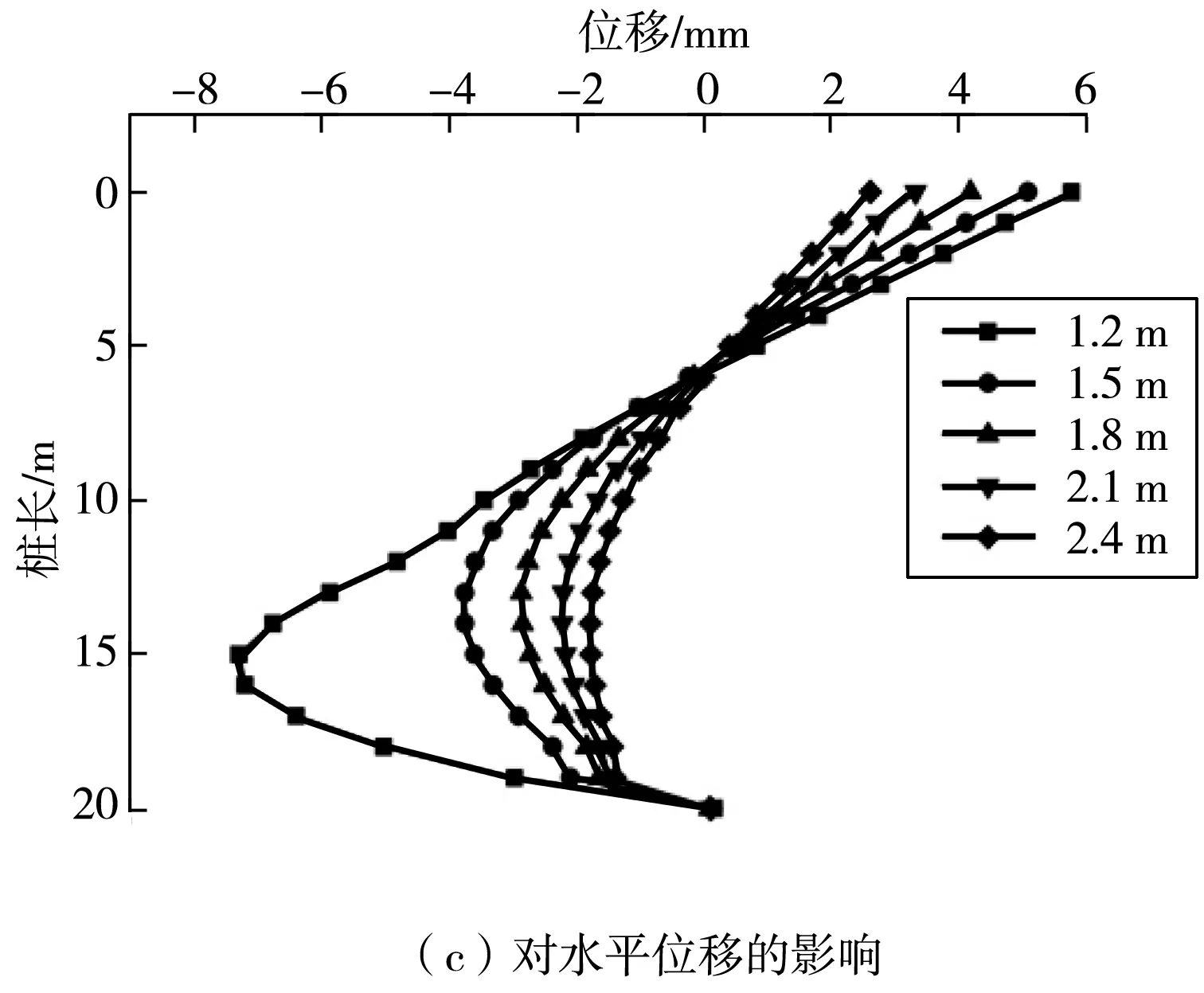
图4 桩直径对性能的影响Fig. 4 Influence of the pile diameter on performance

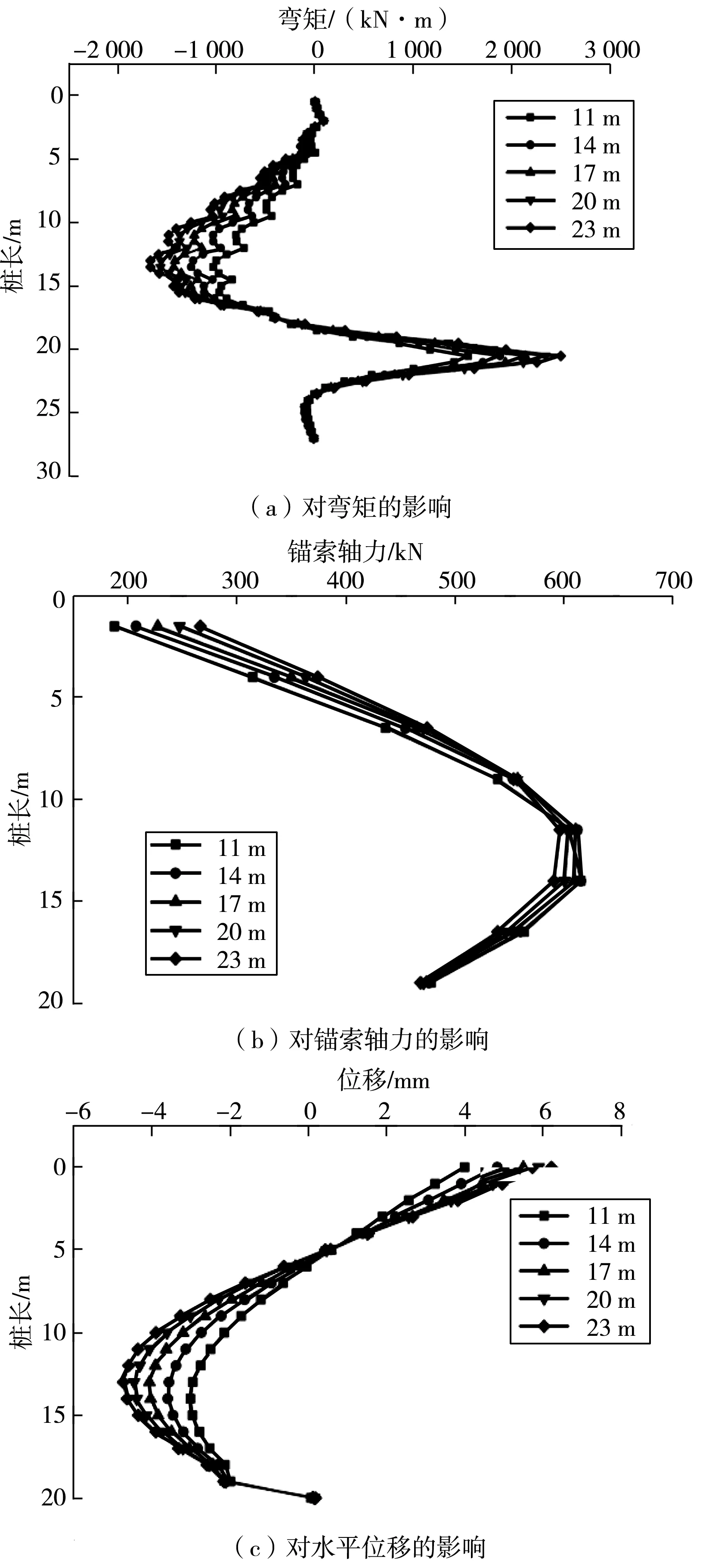
图5 相邻基坑间距对性能的影响Fig. 5 Influence of the spacing of adjacentfoundation pits on performance

由图5(a)可知：随着基坑间距增大，桩身弯矩呈增长趋势，但随着基坑间距增加，弯矩的增长趋势逐渐变缓，间距23、25 m情况相差不大。不同间距下弯矩值的差异主要体现在基坑底面两侧最大极值点处，而其他位置差异较小。相邻基坑间距由11 m增大到23 m，桩身最大弯矩由1 556 kN·m增长为2 497 kN·m，增长值941 kN·m，最大弯矩值为11 m时的1.6倍。

由图5(b)可知：相邻基坑间距由11 m增大到23 m，锚索最大轴力由665 kN减小为646 kN，总体上基坑间距的变化对锚索轴力的影响不大。

由图5(c)可知：随着基坑间距增大，桩后土体位移呈增长趋势，但随着基坑间距增加，位移的增长速度逐渐变缓，同样桩身弯矩也存在这一现象，这是由于当基坑间距大于破裂线水平投影长度后，桩后土压力增加缓慢的原因引起。

3.4 预应力对性能的影响

保持其他参数同2.2节中所述基本方案一致，仅调整锚索预应力，建立锚索预应力为300、400、500、600、700 kN这 5种工况下的计算模型，分别获得沿桩深度方向的桩身弯矩、锚索轴力、桩后土体水平位移变化曲线(图6)。

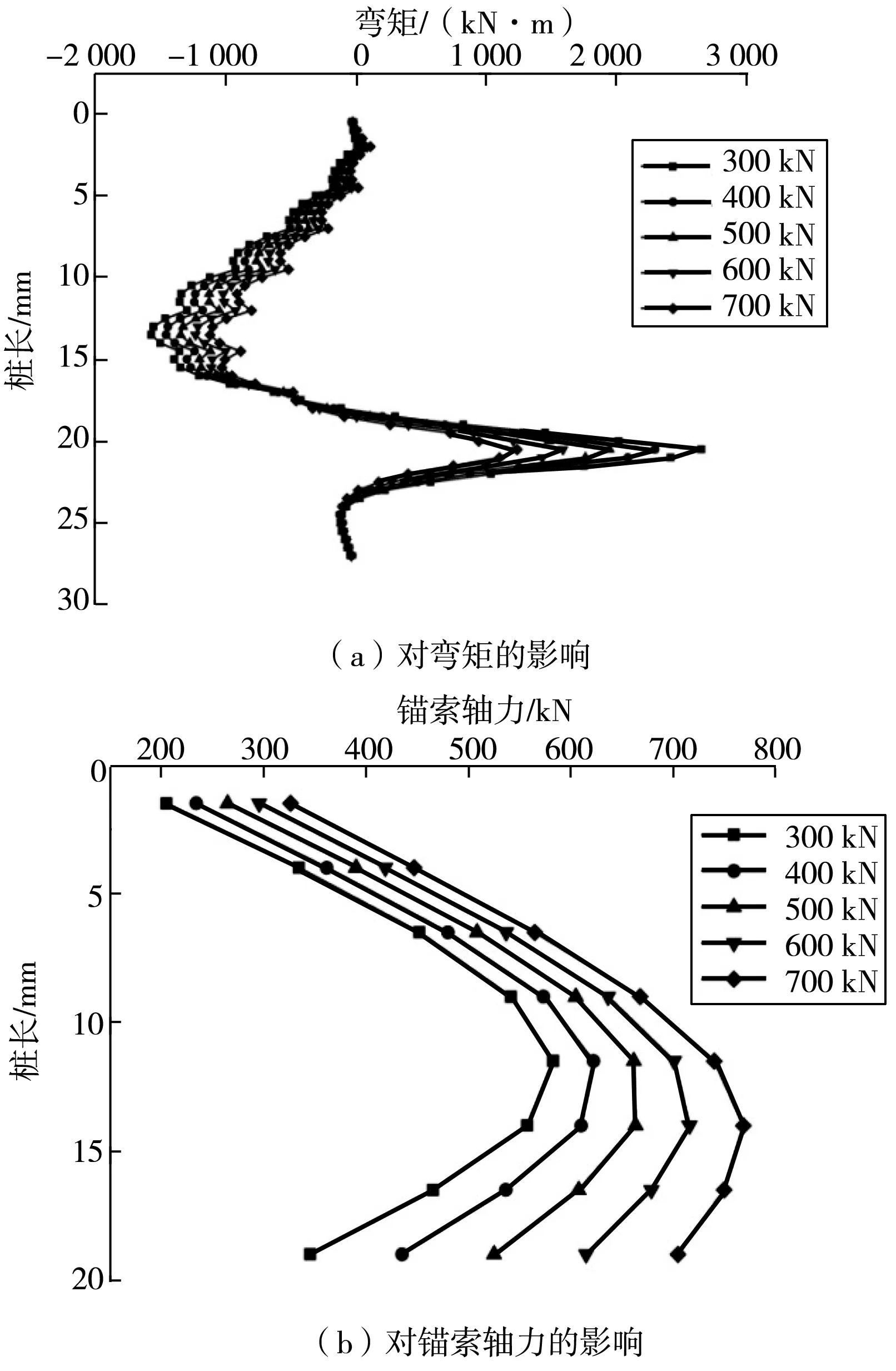
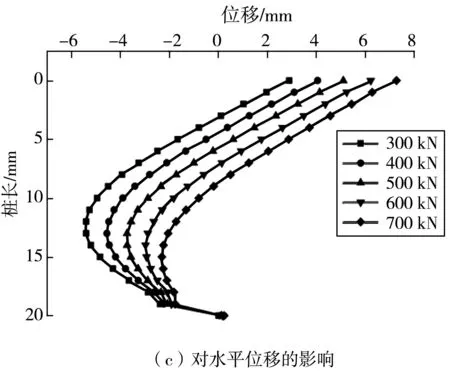
图6 锚索预应力对性能的影响Fig. 6 Influence of the prestressed anchor cable on performance

由图6(a)可知：桩身弯矩随着锚索预应力增加而变小，特别是基坑底面以下的弯矩极值大幅减小。锚索预应力由300 kN增大到700 kN，桩身最大弯矩由2 679 kN·m减小为1 263 kN·m，减少值为1 416 kN·m，最大弯矩值为300 kN时的0.47倍。这意味着可通过增大预应力方式，显著减小桩身的控制弯矩，从而减少桩的配筋，有效节约工程造价。

由图6(b)可知：随着锚索预应力增大，锚索轴力呈增长趋势，越接近基坑底部增长的幅度越大。锚索预应力由300 kN增大到700 kN，锚索最大轴力由583 kN增大为769 kN，增大值为186 kN，最大轴力为300 kN时的1.32倍。

由图6(c)可知：不同预应力作用下，桩后土体位移并不是简单地变大或变小，而是呈现一种整体向基坑外侧偏移的趋势。

3.5 桩间距对性能的影响

保持其他参数同2.2节中所述基本方案一致，仅调整桩间距，建立桩间距为2.0、2.5、3.0、3.5、4.0 m这5种工况下的计算模型，分别获得沿桩深度方向的桩身弯矩、锚索轴力、桩后土体水平位移变化曲线(图7)。

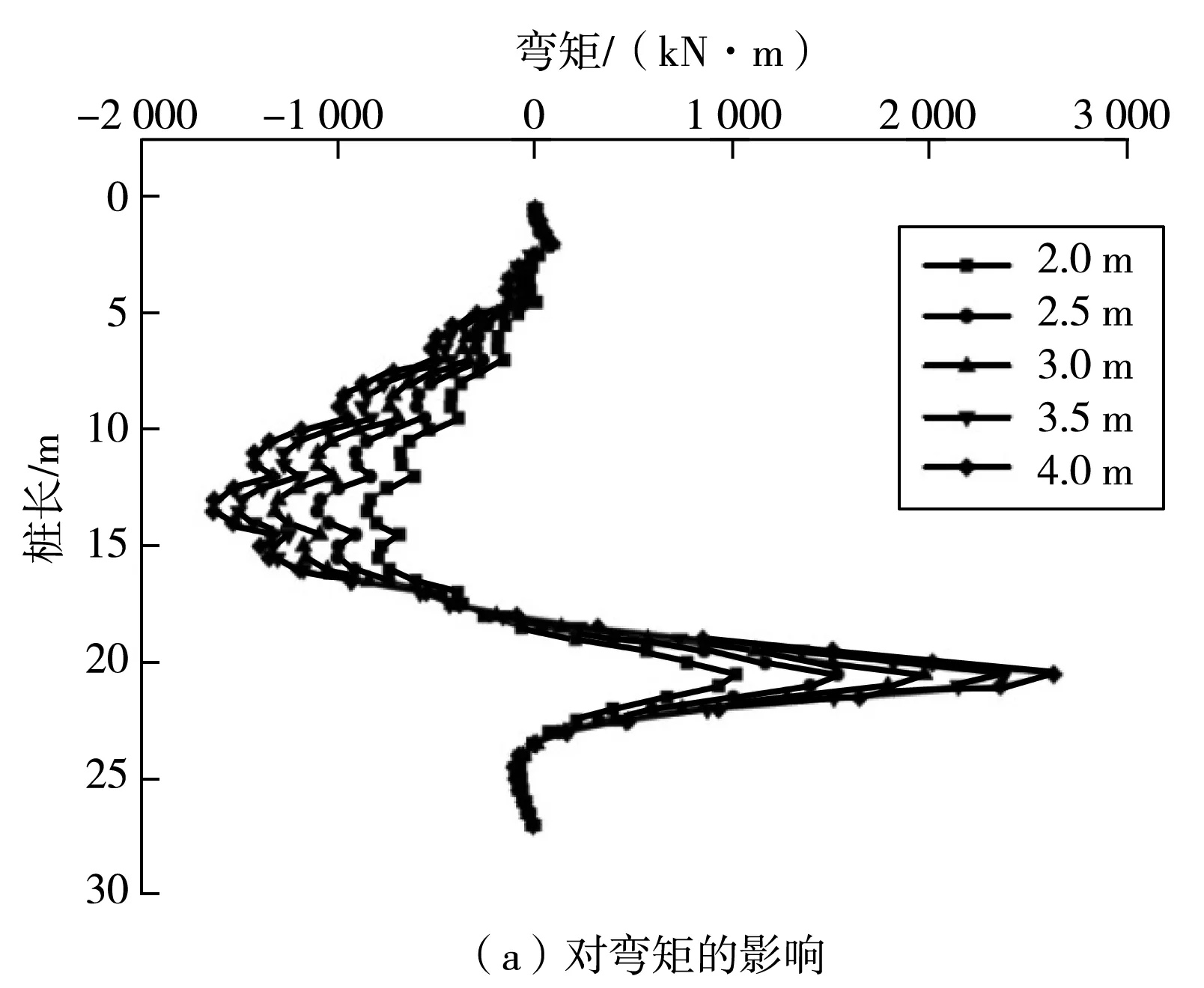
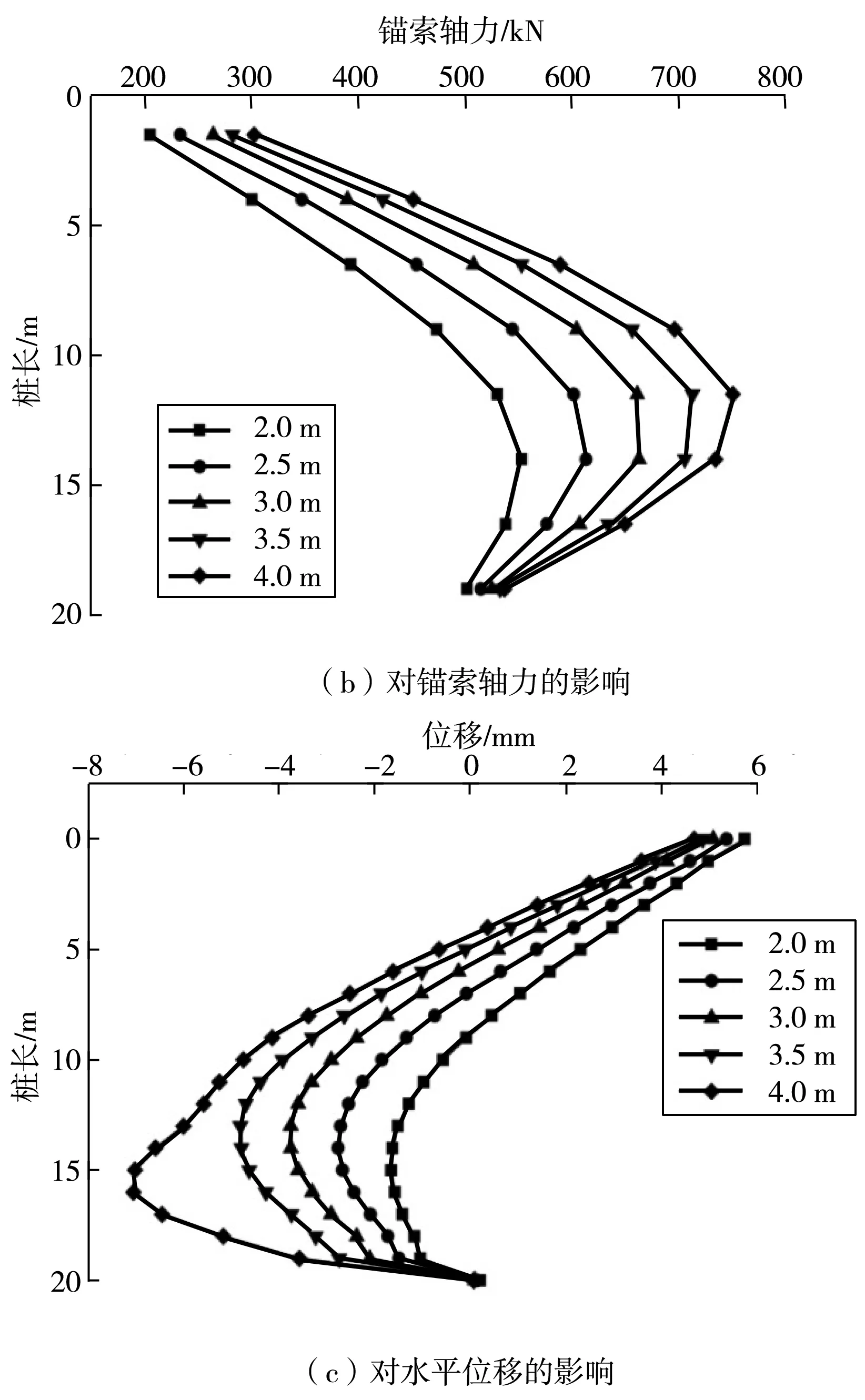
图7 桩间距对性能的影响Fig. 7 Influence of the pile spacing on performance

由图7(a)可知：桩身弯矩沿桩深度方向呈“S形”，且控制弯矩都位于嵌固段。桩间距由2 m增大到4 m，桩身最大弯矩由930 kN·m增大为2 359 kN·m，增大值为1 426 kN·m，最大弯矩值为2 m时的2.54倍。可见桩身弯矩对桩间距比较敏感，因此要综合考虑造价和支护效果等因素，选择合理桩间距。

由图7(b)可知：由于基坑底部位移较小，最下一排锚索轴力基本和预加轴向拉力值保持一致。桩间距由2 m增大到4 m，锚索最大轴力由553 kN增大为751 kN，增大值为198 kN，最大轴力值为2 m时的1.36倍。

由图7(c)可知：随着桩间距增大，桩后土体位移呈现一种整体向基坑内侧偏移的趋势，当间距大于3.5 m时位移增长迅速，建议桩间距不宜大于3倍桩径。

3.6 桩嵌固段长度对性能的影响

保持其他参数同2.2节中所述基本方案一致，仅调整桩嵌固段长度，建立嵌固段为4、5、6、7、8 m这5种工况下的计算模型，获得沿桩深度方向的桩身弯矩、锚索轴力、桩后土体水平位移曲线没有变化。这意味：当嵌固长度满足一定深度后，嵌固长度变化对桩身弯矩、预应力锚索轴力、桩后土体位移没有影响，嵌固长度可取3倍桩径。在实际工程要合理选择桩嵌固段长度，节约工程造价。

4 结 论

1)预应力锚索的设置使桩身弯矩局部呈“波浪形”。锚索锚固在桩上和预应力的存在使桩顶后土体位移并不是偏向基坑一侧，而是出现反向位移。

2)随着桩直径增大、桩身抗弯能力提高，桩身弯矩呈现出“波浪形”这一特点逐渐变弱。桩的有效抗弯长度随着桩径增大而变长。各排锚索轴力分布因桩直径的增大而变的更加“均匀”。桩后土体位移分布也更加“均匀”，建议桩径不小于1.5 m。

3)随着基坑间距增大，桩身弯矩和桩后土体位移呈增长趋势，但随着基坑间距增加，增长速度逐渐变缓，这是由于当基坑间距大于破裂线水平投影长度后，桩后土压力增加缓慢的原因引起的。

4)可通过增大预应力方式，显著减小桩身的控制弯矩，从而减少桩的配筋，有效节约工程造价。

5)桩身弯矩沿桩深整体呈“S形”，且控制弯矩都位于嵌固段，建议桩间距不宜大于3倍桩径。

6)当嵌固长度满足一定深度后，嵌固长度变化对桩身弯矩、预应力锚索轴力、桩后土体位移没有影响，故嵌固长度可取3倍桩径。

[1]刘芳玲，陈文峰，李安元.预应力对拉锚杆技术在深基坑工程中的研究与应用[J].施工技术，2016，45(7)：34-36.

LIU Fangling, CHEN Wenfeng, LI Anyuan. Research and application of pulling anchor prestressed technology in deep foundation excavation engineering[J].ConstructionTechnology, 2016, 45(7): 34-36.

[2]欧阳仲春.对拉式挡土墙拉杆的内力分析[J].土木工程学报，1986，19(2)：65-69.

OUYANG Zhongchun. Analysis of tension in tie rods in tied double retaining walls[J].ChinaCivilEngineeringJournal, 1986, 19(2): 65-69.

[3]康景文，朱丹，王亨林.对拉式挡土墙极限状态设计法[J].西部探矿工程，2004(4)：21-23.

KANG Jingwen, ZHU Dan, WANG Henglin. Limit state design on pulling anchor supporting structure[J].West-ChinaExplorationEngineering, 2004(4): 21-23.

[4]张宏博，解全一，岳红亚，等.对拉式挡土墙稳定性模型试验研究[J].混凝土与水泥制品，2016(4)：85-89.

ZHANG Hongbo, XIE Quanyi, YUE Hongya, et al. Research on stability of pulling anchor supporting structure based on laboratory model test[J].ChinaConcreteandCementProducts, 2016(4): 85-89.

[5]孙书伟，林杭，任连伟.FLAC3D在岩土工程中的应用[M].北京：中国水利水电出版社，2011：182-194.

SUN Shuwei, LIN Hang, REN Lianwei.TheApplicationofFLAC3DtoGeotechnicalEngineering[M]. Beijing: China Water & Power Press, 2011: 182-194.

[6]任秀文，谭亮，冯樊.竖向荷载作用下预制管桩桩土共同作用的数值分析[J].重庆交通大学学报(自然科学版)，2011，30(增刊1)：550-554.

REN Xiuwen, TAN Liang, FENG Fan. Numerical analysis on pile-soil interaction of precast pipe pile under vertical loading[J].ChongqingJiaotongUniversity(NaturalScience),2011,30(Sup1): 550-554.

[7]吴珺华，杨松.超固结膨胀土抗剪强度特性及边坡稳定研究[J].重庆交通大学学报(自然科学版)，2016，35(4)：70-74.

WU Junhua, YANG Song. Study on shear strength property of over-consolidated expansive soil and slope stability[J].ChongqingJiaotongUniversity(NaturalScience), 2016, 35(4): 70-74.

[8]陈育民，许鼎平.FLAC/FLAC3D基础与工程实例[M].北京：中国水利水电出版社，2013：176-177.

CHEN Yumin, XU Dingping.FundamentalsofFLAC/FLAC3DwithEngineeringExample[M]. Beijing: China Water & Power Press, 2013: 176-177.

[9]吴润泽，周海清，胡源，等.基于FLAC3D的锚索抗滑桩滑坡推力分布规律研究[J].防灾减灾工程学报，2013，33(5)：548-555.

WU Runze, ZHOU Haiqing, HU Yuan, et al. Research on distribution law of landslide thrust of anchored anti-slide pile based on FLAC3D[J].JournalofDisasterPreventionandMitigationEngineering, 2013, 33(5): 548-555.

[10]刘赪炜，韩煊.单桩数值模拟参数与方法的研究[J].岩土工程学报，2010，32(增刊2)：204-207.

LIU Chengwei, HAN Xuan. Method and parameters of numerical simulation on single pile[J].ChineseJournalofGeotechnicalEngineering, 2010, 32(Sup2): 204-207.

[11]肖昭然.单桩分析的双曲线模型及相应参数的确定[J].土工基础，2002，16(3)：60-63.

XIAO Zhaoran. Determination of hyperbolic model and its corresponding parameters in single-pile analysis[J].SoilEngineeringandFoundation,2002,16(3):60-63.

[12]杜晓霞.上部结构-桩筏基础-地基共同作用的非线性数值模拟[D].南京：南京理工大学，2005.

DU Xiaoxia.NonlinearNumericalModifyofUpperStructure-PiledRaftFoundation-SoilInteraction[D]. Nanjing: Nanjing University of Science and Technology, 2005.