液压式动力反共振隔振器带宽分析
肖 晗, 董兴建, 彭志科, 孟 光
(上海交通大学 机械系统与振动国家重点实验室振动与冲击、噪声研究所,上海 200240)
动力反共振隔振是一种新型隔振技术,其突出优势是在不降低系统静刚度的条件下实现线谱振动的隔离,并且在反共振频率上具有非常高的隔振效率,通常可达95%以上[1]。这一优势使得动力反共振隔振成功地解决了直升机主减-机身的低频隔振问题:既隔离了主减到机身的线谱振动,又不降低主减与机身之间的静刚度。动力反共振隔振的惯性放大机制主要由机械杠杆或液压杠杆来实现。Flannelly等[2-5]给出了不同形式的机械式动力反共振隔振器,并成功应用在NH90、BO105等轻中型直升机中。1980年,Braun[6-7]提出了一种液压式动力反共振隔振器,并在EC135等直升机上得到应用,显示出良好的隔振性能。相比机械式动力反共振隔振器,液压式动力反共振隔振器具有结构对称,安装方便,低阻尼和低噪声等优点[8],应用前景广阔。
动力反共振隔振器具有较强的频率选择性,限制了其应用的范围。为了在较宽的频带内实现动力反共振隔振,有必要分析动力反共振隔振器的带宽并对其进行优化设计,为动力反共振隔振器的宽频带设计提供理论指导[9-10]。在某种意义上,动力反共振隔振器可以看作一种陷波滤波器,其带宽定义为隔振器在给定传递率下实现有效振动衰减的频率范围[11-12]。对于液压式动力反共振隔振的带宽设计,目前鲜见文献报导。建立了两种液压式动力反共振隔振器模型,讨论了隔振带宽与惯性元件质量、放大比等参数的关系;给出了一种双层隔振器设计思路,以实现宽频带反共振隔振。
1 液压式动力反共振隔振器带宽
液压式动力反共振隔振器由弹簧、大小波纹管和惯性质量块构成。当给基座施加激励时,金属波纹管内的流体会发生往复运动,在特定激励频率下,由流体运动产生的动压力与弹簧提供的弹性力相平衡,阻断了振动向隔振对象的传递,从而使得隔振对象位移为零。这一频率即为反共振频率。
相比传统的动力吸振器,反共振隔振器通过引入惯性放大机构,能以较小的附加质量实现较好的隔振效果。机械式动力反共振隔振器通过机械式杠杆来实现惯性放大,液压式动力反共振隔振器通过两个不同截面积的金属波纹管来实现惯性放大。根据波纹管的安装形式,提出了两种类型的液压式动力反共振隔振器,Ⅰ型和Ⅱ型,分别讨论了它们的隔振带宽。
1.1 Ⅰ型液压式反共振动力隔振器
图1为Ⅰ型动力反共振隔振器的原理图,隔振器置于基座和隔振对象之间,其中Ap为大波纹管有效横截面积;As为小波纹管有效横截面积;k为弹簧刚度;x为隔振对象位移;y为基座位移;z为惯性质量位移;m为隔振对象质量;mis为惯性元件质量,定义放大比为α=Ap/As且α>1,假设水不可压缩,流体体积不变。根据流体连续性方程,得到位移关系
(1)
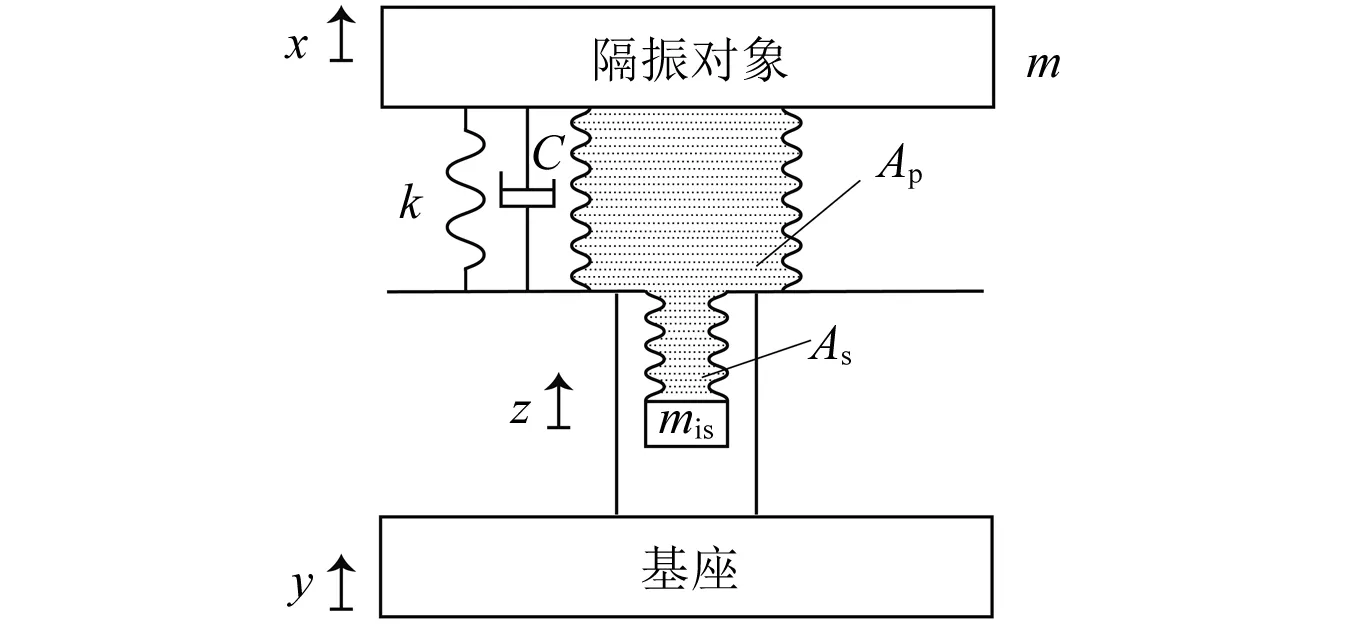
图1 Ⅰ型液压式动力反共振隔振器Fig.1 Type Ⅰ hydraulic anti-resonant vibration isolator
动力学方程可以写为
(2)
(3)
对基座施加简谐激励, 记x=Xeiωt,y=Yeiωt, 根据式(2)和式(3)可以得到系统的极点
(4)
以及系统的零点
(5)
系统的位移传递率为
(6)
更进一步,可以得到
(7)
仅要求系统在反共振点具有隔振特性是不够的,一般情况下,我们更关心隔振器在多大的频率范围内具有良好的隔振性能。对基座施加位移激励,如果允许的最大位移传递率为T0, 那么将位移传递率绝对值小于T0的频率范围称为隔振带宽(Bandwidth)。将隔振带宽的中心频率定义为系统零点ωz, 记N=ω0/ωz。
在给定最大位移传递率T0的情况下, 对式(6)取绝对值并令其等于T0, 可以得到两个解,即系统的下截止频率ωs1和上截止频率ωs2(ωs1<ωs2)。进行归一化处理,定义隔振带宽为
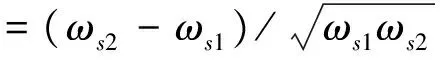
(8)
为了便于求解截止频率,引入以下关系
(9)
进一步,确定式(8)中的l和m即可确定截止频率。
由式(5)可得
(10)
由式(4)、式(5) 和式(10)得到零极点的关系
(11)
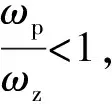
将式(10)代入式(6)并令之为-T0,可以得到
(12)
同样地,将式(10)代入式(6)并令之为T0,可以得到
(13)
由式(8)和式(9)有
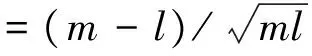
(14)
将式(12)、式(13)代入式(14),即可得到隔振带宽的表达式
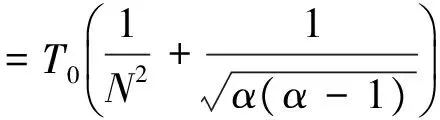
(15)
对于低频隔振,那么N>1。最大位移传递率与隔振要求有关,一般应满足T0≪1。但是,如果T0过小,会使得隔振频带过窄,这样就难以满足实际的隔振要求,在实际的应用中过低的最大位移传递率并没有必要。根据式(15),可以计算出一定质量比和频率比条件下的隔振带宽。
记f=ω/ω0, 给定N=2,μ=0.1, 作出传递率绝对值随f的变化图。图2为Ⅰ型隔振器位移传递率绝对值图。
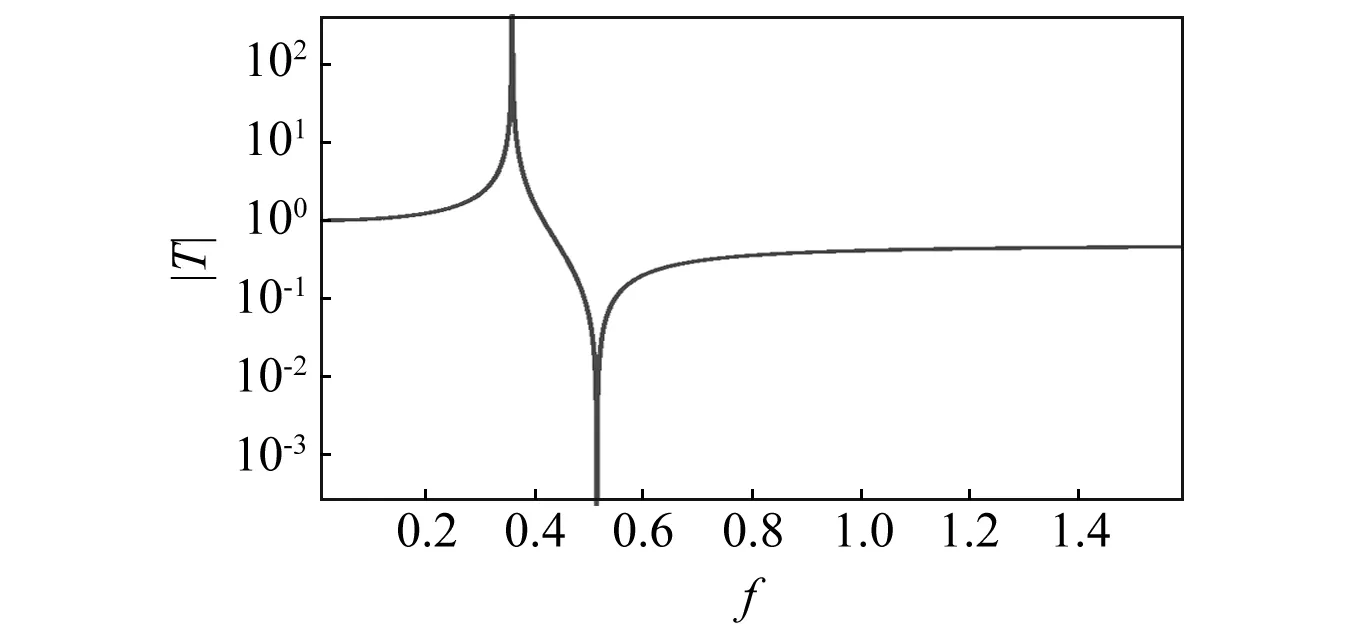
图2 Ⅰ型隔振器位移传递率绝对值图Fig.2 Transmissibility plots showing the bandwidth of a type Ⅰ isolator
从图2中可见,Ⅰ型液压式反共振隔振器在反共振点周围一定频率范围内形成隔振带宽,如果位移传递率为0.1,则隔振带宽为0.042 2。
1.2 Ⅱ型液压式反共振动力隔振器
图3是Ⅱ型液压式反共振隔振器形式,它与Ⅰ型隔振器原理相同,但惯性质量和和隔振对象具有不同的相对运动方向,忽略阻尼,其动力学方程为
(16)
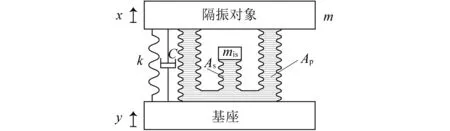
图3 Ⅱ型液压式动力反共振隔振器Fig.3 Type Ⅱ hydraulic anti-resonant vibration isolator
系统的位移传递率为
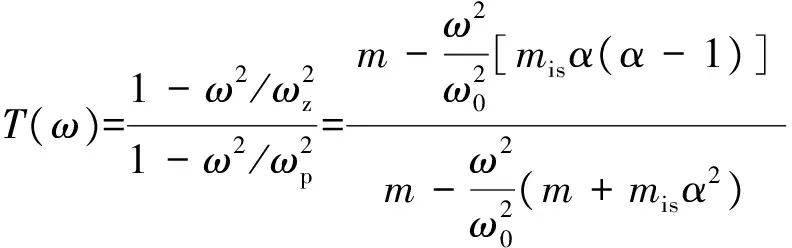
(17)
根据式(16)可以得到Ⅱ型隔振器零极点位置关系
(18)
从式(17)可以看出,Ⅱ型液压式反共振隔振器的零极点大小关系并不明确,选取不同的放大比α,零极点的大小关系将会发生变化。
采用同样的方法,可以得到Ⅱ型隔振器隔振带宽表达式
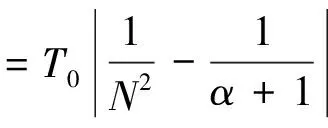
(19)
同样,在N=2,μ=0.1时, 作位移传递率绝对值图。图4为Ⅱ型隔振器位移传递率绝对值曲线。
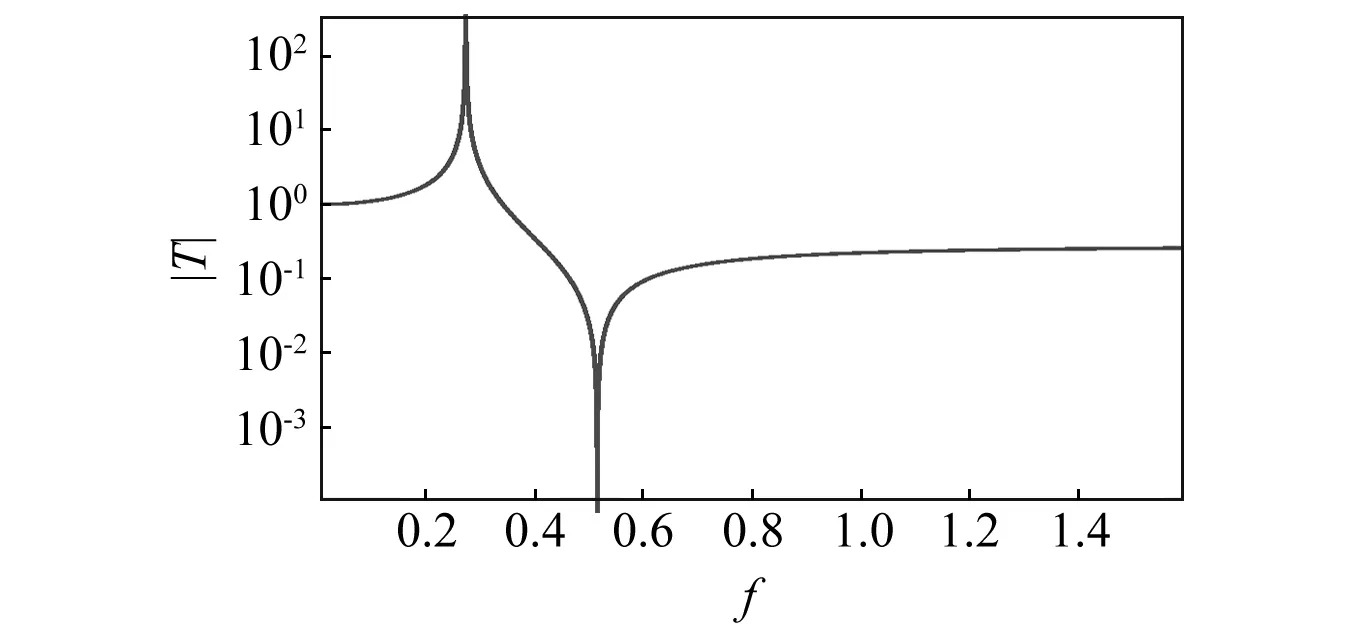
图4 Ⅱ型隔振器位移传递率绝对值图Fig.4 Transmissibility plots showing the bandwidth of a type Ⅱ isolator
图2和图4表明,Ⅰ型和Ⅱ型隔振器具有相同的隔振原理,如果位移传递率为0.1,Ⅱ型隔振器的隔振带宽为0.010 2,比Ⅰ型隔振器带宽要小。
2 隔振器带宽分析
下面对Ⅰ型和Ⅱ型液压式反共振隔振器带宽进行比较。
图5是T0=0.05时,带宽随放大比α以及N的变化关系图。可以看出,对Ⅰ型和Ⅱ型液压式动力反共振隔振器,在α和N取一定值的时候,都会出现隔振带宽最小的情况。从图中还可以看出,隔振带宽可以无限大,但此时需要很小的α或者N,在工程设计中没有意义。
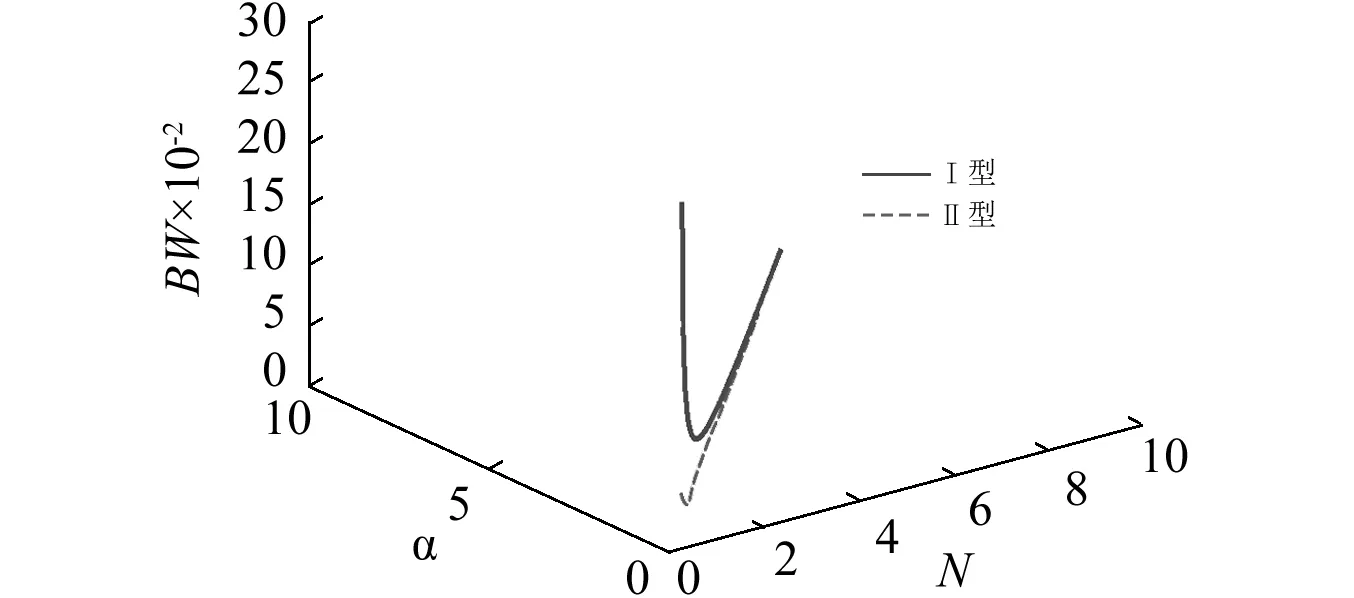
图5 带宽随α,N变化图Fig.5 Bandwidth versus α and N comparisons
取位移传递率T0=0.05, 图6为N=2时隔振带宽与放大比α的关系, 图7是隔振带宽与N的关系。
从图6可以看出,在固定N为2 的时候,Ⅰ型隔振器比Ⅱ型隔振器具有更大的带宽。Ⅰ型隔振器的带宽随着放大比增大而降低,Ⅱ型隔振器不同,在放大比为3的时候带宽为0,也即没有隔振效果,接着随着放大比增加带宽增加。理论上,取较小的放大比可以得到较大的带宽,但由式(10)可以看出,放大比和质量比呈负相关关系,如果α→1, 则μ→∞。 这意味着,如果采取很小的放大比,则需要非常大的惯性质量,这在工程设计中也是没有意义的。
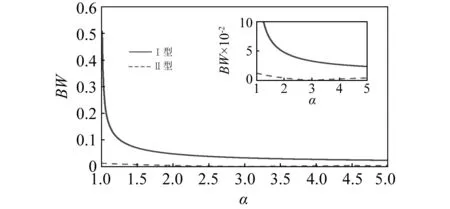
图6 带宽随放大比α变化图Fig.6 Bandwidth versus α comparisons
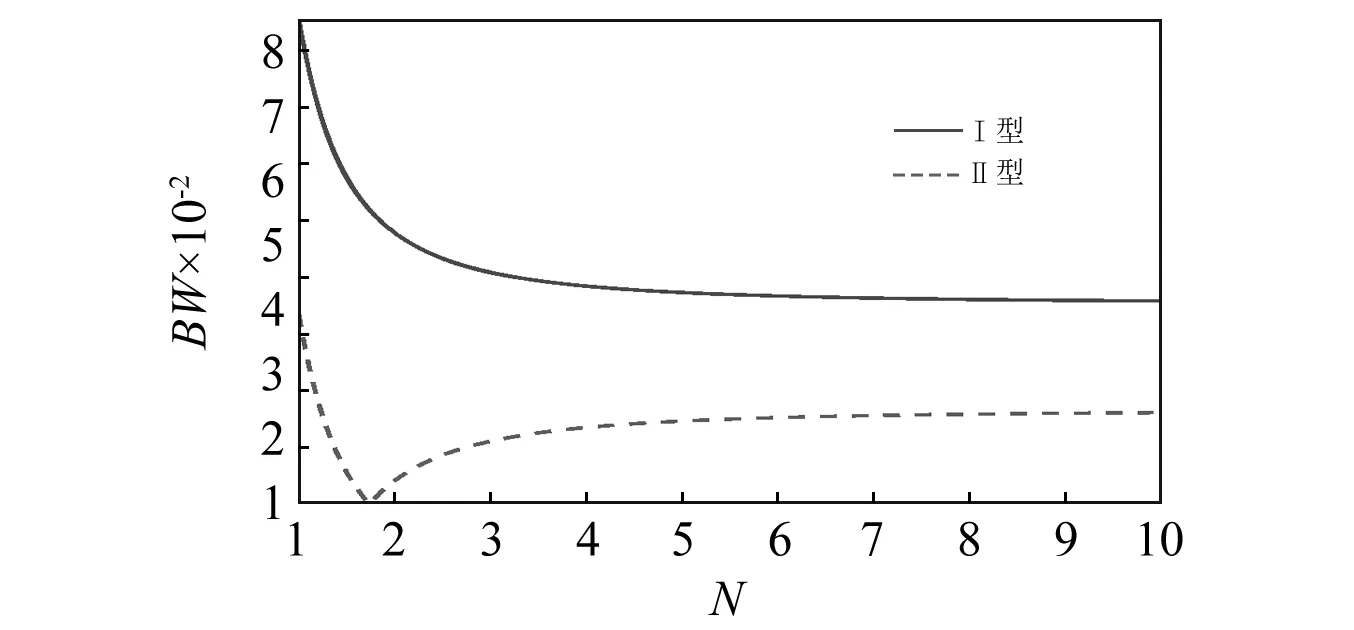
图7 带宽随频率比N变化图Fig.7 Bandwidth versus N comparisons
同样,从图7可以看出,在固定放大比α为2的时候,Ⅰ型隔振器带宽随着频率比增大而减小,而Ⅱ型隔振器仍会出现带宽为0的情况。类似地,取较小的频率比可以得到较大的带宽,但是由于低频应用的条件,希望反共振频率要适当小于系统无阻尼自然频率,这时可根据实际需要确定相应的频率比。
对于不同的放大比和频率比,Ⅰ型隔振器的隔振带宽总是大于Ⅱ型隔振器的隔振带宽。在单自由度隔振系统中,采用Ⅰ型隔振器比Ⅱ型隔振器具有更好的效果。
3 双层液压式反共振隔振器设计
3.1 动力学模型
前面已经讨论了两种单自由度液压式反共振隔振器,可以看到,隔振器在反共振频率周围形成了隔振带宽。如果再引入其它的反共振点,并且使这些反共振点接近,则可以进一步扩大带宽。理论上,可以引入尽可能多的反共振点,考虑到实际情况,只讨论2自由度的情况。
图8为一种双层液压式反共振隔振器的设计。它分为上下两层,下层为Ⅱ型液压式反共振隔振器,上层为Ⅰ型液压式反共振隔振器。记Ⅰ、Ⅱ型隔振器零点分别为ωz Ⅰ和ωz Ⅱ,极点分别为ωp Ⅰ和ωp Ⅱ。为了得到较大的带宽,可以使Ⅱ型隔振器满足ωz Ⅱ<ωp Ⅱ, 而Ⅰ型隔振器始终满足ωp Ⅰ<ωz Ⅰ,从而实现
ωp Ⅰ<ωz Ⅰ<ωz Ⅱ<ωp Ⅱ
(20)
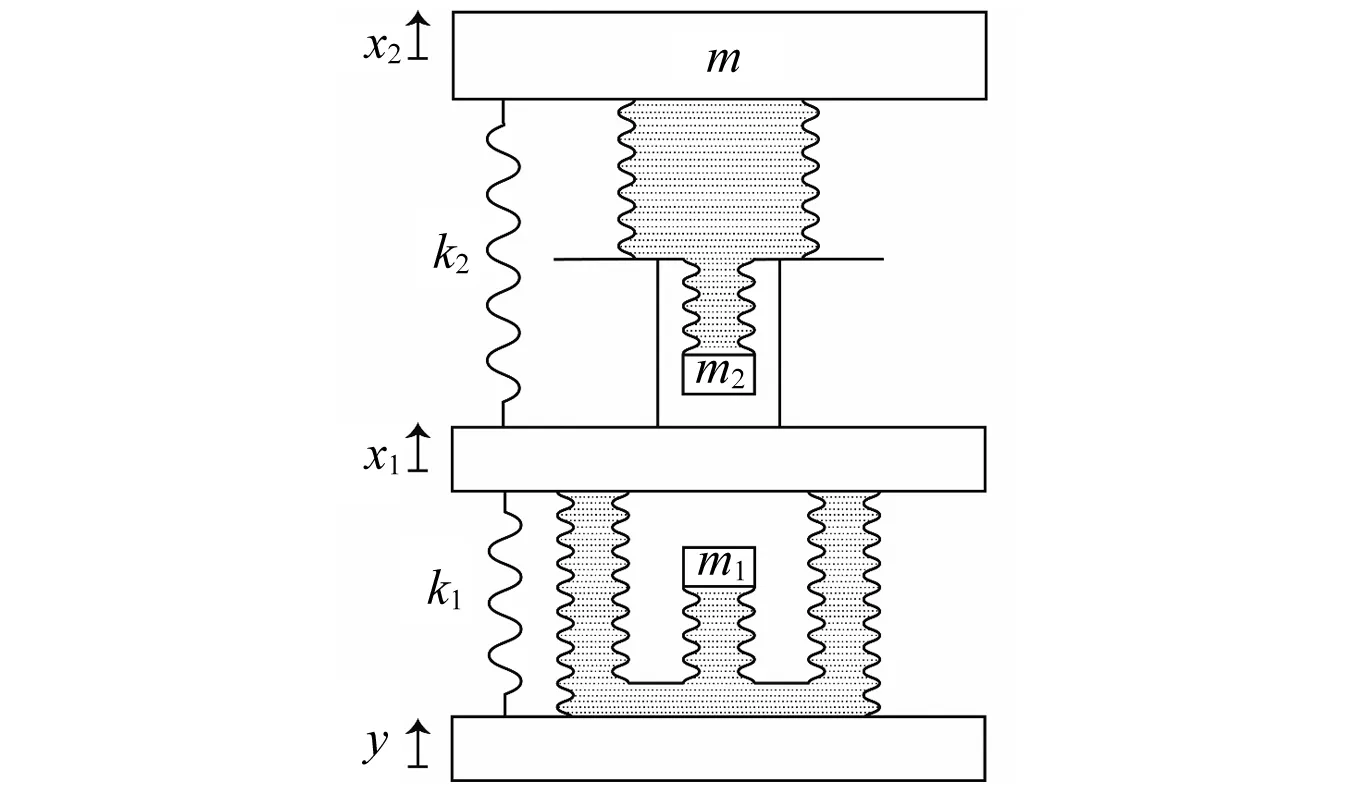
图8 双层液压式反共振隔振器Fig.8 2-dof hydraulic anti-resonant vibration isolator
该系统的动力学方程为
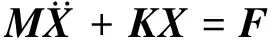
(21)
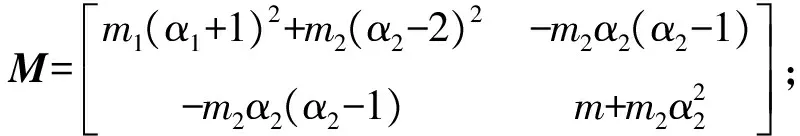
系统的位移传递率为
(22)
其中,
进一步,可以将式(22)改写成
(23)
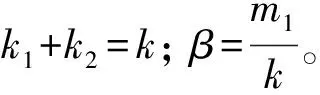
从式(21)可以看出,双层隔振器的零点表达式与单层一样,但极点形式发生了变化。记系统零极点为ωz1,ωz2,ωp1,ωp1。则为
ωz1=ωz Ⅰ,ωz2=ωz Ⅱ
(24)
记较小的极点为ωp1, 下面比较ωp1和ωp Ⅰ的大小。 考虑ωp Ⅰ时,可将第一层隔振器和基座看作一个整体,隔振器工作时,系统弹簧处于同时拉伸或压缩的状态,此时作用在上层上的力减小,从而有ωp1<ωp Ⅰ。
另一方面,比较ωp2和ωp Ⅱ的大小。 考虑ωp Ⅱ时,可将上层隔振器和隔振对象看做一个整体,隔振器工作时,上下层弹簧状态不同,这将导致作用在下层上的力增加,因而有ωp Ⅱ<ωp2。
由以上讨论可以得到双层液压式反共振隔振器的零极点位置关系
ωp1<ωz1<ωz2<ωp2
(25)
3.2 隔振带宽优化设计
确定系统允许的最大传达率T0后, 由T(ω)=-T0可以得到隔振带宽的截止频率ωs1和ωs2。由于在系统带宽范围内存在两个零点,因此在带宽内存在使得传递率绝对值取最大值的频率,记该频率为ωm。优化目标函数为
约束条件
k1,k2≥k,m1,m2≥0,α1,α2≥1
在优化过程中,有6个变量,m1,m2,k1,k2,α1,α2。将m2,k2,α1,α2称为过程变量,剩下的m1,k1称为决策变量。根据h2和h3可以解得m2和k2。通过h1和h4确定α1和α2。 给定μ,N,T0,m和k均取为1。根据设定的初始条件,采用遗传算法进行优化,得到m1和k1,从而得到4个过程变量,结果见表1和表2。

表1 μ=0.1, N=2, T0=0.05时,优化结果
从图9可以看出,双层隔振器有两个反共振点,给定最大位移传递率时,利用两个反共振点附近的频率范围得到隔振带宽。双层隔振器相比于Ⅰ型隔振器具有更大的带宽,将近2.26倍。图9中的局部最大值即为给定的最大位移传递率。

表2 μ=0.5, N=2, T0=0.05时,优化结果
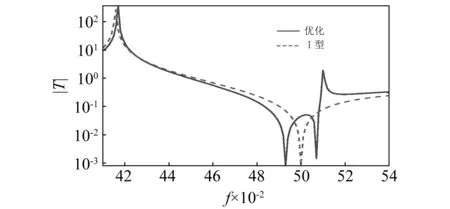
图9 优化结果与Ⅱ型隔振器比Fig.9 Bandwidth comparison of the 2-dof optimum design and a type Ⅱ isolator
图9和图10表明,较大的质量比可以得到更大的带宽。然而,提高质量比会增加系统负担,实际设计过程中应该综合来考虑。
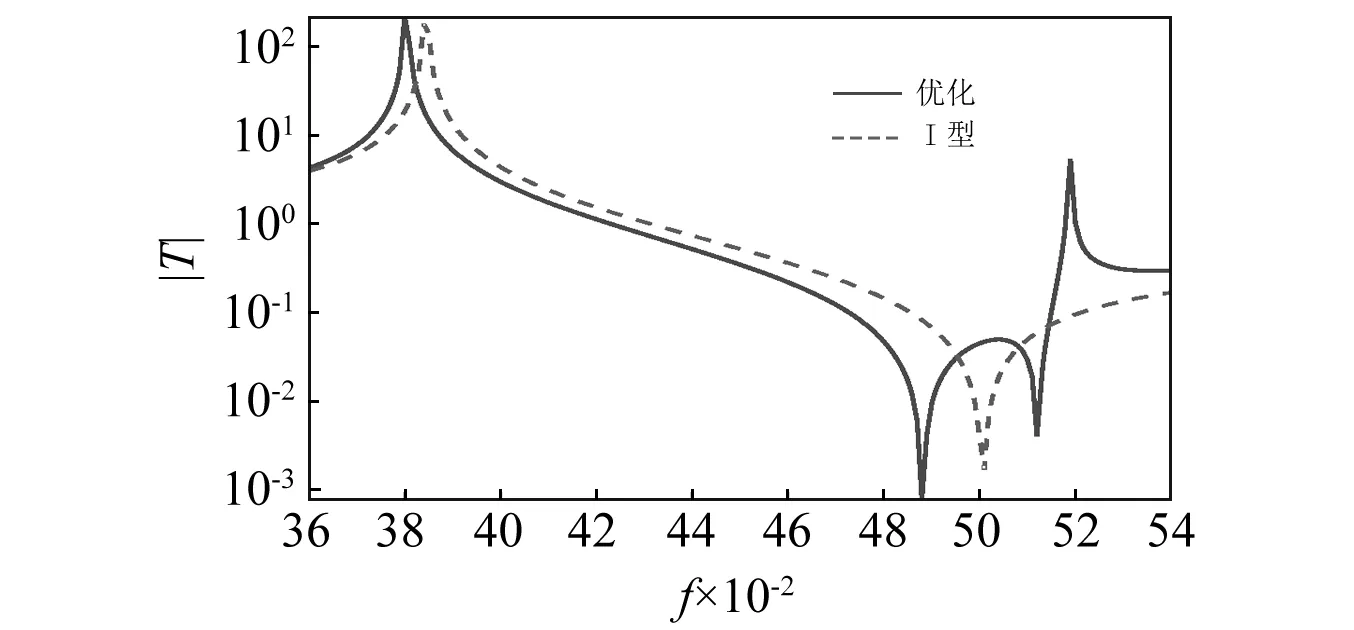
图10 优化结果与Ⅱ型隔振器比较Fig.10 Bandwidth comparison of the 2-dof optimum design and a type Ⅱ isolator
4 结 论
建立了液压式动力反共振隔振器的带宽表达式, 带宽随α的增加而减小, 随N的减小而增加。选择尽可能小的放大比可以得到较大的带宽,但此时隔振系统所需的惯性质量过大,这在实际设计中是要避免的。同时,N的减小与通常低频隔振的要求相违背,因此,在液压式动力反共振隔振器的带宽设计中,要综合考虑α和N对带宽的影响,并避开使得带宽最小的α和N的取值。最后,提出了一种双层液压式动力反共振隔振器,优化分析表明,在给定最大位移传递率时,通过选取隔振器的参数,可以获得最大的隔振带宽。与Ⅰ型隔振器相比,双层隔振器比单层隔振器具有更大的隔振带宽。
[ 1 ] 顾仲权. 动力反共振隔振[J]. 噪声与振动控制, 1989(6): 36-40.
GU Zhongquan. Dynamic anti resonance vibration isolation [J]. Noise and Vibration Control, 1989(6): 36-40.
[ 2 ] FLANNELLY W G. Dynamic antiresonant vibration isolator: U.S. 3,322,379 [P]. 1967-05-26.
[ 3 ] RITA A D, MCGARVEY J H, JONES R. Helicopter rotor isolation evaluation utilizing the dynamic antiresonant vibration isolator [J]. Journal of the American Helicopter Society, 1976, 23(1): 22.
[ 4 ] DESJARDINS R A. Vibration isolation system: U.S. 4,140,028 [P]. 1979.
[ 5 ] DESJARDINS R A, HOOPER W E. Antiresonant rotor isolation for vibration reduction [J]. Journal of the American Helicopter Society, 1980, 25(3): 46-55.
[ 6 ] BRAUN D. Development of antiresonance force isolators for helicopter vibration reduction [J]. Journal of the American Helicopter Society, 1982, 27(4): 37-44.
[ 7 ] BRAUN D. Vibration isolator particularly of the antiresonance force type: U.S. 4,781,363 [P]. 1988-11-01.
[ 8 ] 孙忠池. 反共振理论在动力吸振器设计中的应用[J]. 应用力学学报, 1993, 10(4): 97-103.
SUN Zhongchi. The application of anti-resonance theory in design of vibration absorbers [J]. Chinese Journal of Applied Mechanics, 1993, 10(4): 97-103.
[ 9 ] YILMAZ C, KIKUCHI N. Analysis and design of passive band-stop filter-type vibration isolators for low-frequency applications [J]. Journal of Sound and Vibration, 2005, 291(3): 1004-1028.
[10] YILMAZ C, KIKUCHI N. Analysis and design of passive low-pass filter-type vibration isolators considering stiffness and mass limitations [J]. Journal of Sound and Vibration, 2006, 293(1): 171-195.
[11] 刘春嵘,冀建飞,徐道临. 反共振流体浮筏的隔振特性研究[J]. 力学与实践, 2012, 34(2): 49-53.
LIU Chunrong, JI Jianfei, XU Daolin. Vibration isolation of fluid-type anti-resonance floating raft system [J]. Mechanics in Engineering, 2012, 34(2): 49-53.
[12] HUANG Xiuchang, JIANG Aihua, ZHANG Zhiyi, et al. Design and optimization of periodic structure mechanical filter in suppression of foundation resonances [J]. Journal of Sound and Vibration, 2011, 330(20): 4689-4712.

