一种结合交互多模型的多机动扩展目标跟踪算法
葛建良,葛洪伟,2,王 冬,杨金龙,2
1(江南大学 物联网工程学院,江苏 无锡 214122) 2(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
1 引 言
传统目标跟踪算法中目标与量测为一一对应关系,因为目标轮廓大小相比于传感器分辨率可忽略不计.而随着传感器分辨率的逐渐提高,这一假设不再适合.在实际场景中,单个目标每帧可能有多个量测,这样的目标称为扩展目标[1,2].扩展目标问题一经提出便成为当前目标跟踪领域的一个研究热点[3-5].
近年来,由于Mahler[6]提出的基于随机有限集合(Random Finite Set,RFS)的多目标跟踪算法可以避免传统多目标跟踪算法中的数据关联过程,因而受到国内外学者的广泛关注.目前,该类算法主要包括概率假设密度滤波、势均概率假设密度滤波器和多伯努利滤波器等[7-9].Vo等分别在非线性条件和线性高斯条件下给出了PHD滤波器的序贯蒙特卡洛(Sequential Monte Carlo)实现和高斯混合(Gaussian mixture)实现:SMC-PHD滤波器[10]和GM-PHD滤波器[11].由于可以避免数据关联过程,基于RFS的多目标跟踪算法尤其适用于多扩展目标跟踪.Gilholm等提出了扩展目标泊松量测模型[12],在此基础上,Mahler根据有限集合统计(FISST)推导出扩展目标概率假设密度(ET-PHD)滤波器[2].随后,Granström等人将ET-PHD滤波器在线性高斯条件下采用GM实现[13].该算法可以有效地实现对多扩展目标的跟踪,但针对多机动扩展目标跟踪时性能将下降,且不能给出各个目标的航迹估计.
机动目标的跟踪中,交互多模型算法是最常使用的方法.Blom和Bar Shalom等人于1988年在广义伪贝叶斯算法的基础上提出一种具有马尔可夫切换系数的交互多模型算法[14],该算法具有超高的高效费比,因而被广泛应用于工程领域.正因为IMM算法的优越性,多国学者又对IMM算法进行深入的研究,如Jilkov等在IMM的基础上提出了自适应交互多模型[15](AIMM);Johnston和Krishnamurthy提出了重新计算权重的交互多模型[16](RIMM)算法;Li和Bar Shalom提出了变结构交互多模型[17](VSMM),这种模型增加了总的模型数,但并未明显增加计算量,具有较好的效果,但由于结构过于复杂,实现起来有很大难度.
上述交互多模型算法主要是应用于机动点目标的跟踪,为了解决多扩展机动目标的跟踪问题,想到在扩展高斯混合概率假设密度滤波算法的框架下,引入交互多模型思想[18],提出一种新的多机动扩展目标跟踪算法,即交互多模型扩展高斯混合概率假设密度(IMM-ET-GMPHD)滤波算法.由于扩展目标区别于传统的点目标,因此引用交互多模型时,文中对算法的结构也进行了推导和改进.该算法采用3个不同模型(匀速运动模型、恒速率左转模型及恒速率右转模型)滤波及更新模型概率,进行交互融合来实现对多机动扩展目标跟踪实现有效地跟踪.在此基础上,考虑到原始的多扩展目标跟踪算法中不能获取各个扩展目标的完整轨迹问题,进一步提出一种高斯分量标识方法,实现了对多机动扩展目标的航迹管理.
2 扩展目标高斯混合概率假设密度滤波器
扩展目标与传统点目标的区别在于在每一时刻可产生多个传感器量测,因此,扩展目标的似然函数模型区别于点目标的似然函数模型,单个扩展目标的伪似然函数可采用泊松模型来描述[12]:
LZk(x)=1-(1-e-γ(x))pD(x)+
(1)
其中,γ(x)表示泊松均值,即:每一时刻量测产生的泊松比,(1-e-γ(x))表示状态为x的扩展目标至少产生一个量测的概率,pD(x)表示传感器的检测概率,则(1-e-γ(x))pD(x)表示有效的检测概率.φzk(x)表示单个目标的似然函数,λkck(zk)表示杂波强度,Zk表示目标的量测集合,P表示量测集合Zk所有的划分,W为每个划分P的单元集,ωp,dW分别为划分集P和单元集W的权值系数.
假设扩展目标的运动模型服从线性高斯分布,扩展目标高斯混合PHD滤波算法递推如下:
1) PHD预测
假设k-1时刻,扩展目标的PHD函数可表示为:
(2)
则k时刻,扩展目标状态的预测PHD函数可表示为:
vk|k-1(x)=rk(x)+vS,k|k-1(x)
(3)
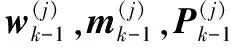
2) PHD更新
k时刻,经过量测更新后的后验PHD函数可表示为:
vk|k(x)=LZk(x)vk|k-1(x)
(4)
其中,LZk(x)为式(1)所示的量测伪似然函数.
3 IMM-ET-GMPHD滤波算法
原始ET-GMPHD算法虽然可以实现对复杂环境下多扩展目标的跟踪,但当目标发生机动时,跟踪性能将下降,甚至出现跟踪不上的问题.交互多模型[19]作为目前机动目标跟踪中比较优越的混合估计式算法,在给定合理的运动模型集合的前提下,IMM可以跟踪目标的任意机动.因此,本文在扩展高斯混合概率假设密度滤波算法的框架下,引入交互多模型的思想,来解决多机动扩展目标的跟踪问题.
在模型上,本文主要采用了三个经典的模型,即:匀速运动模型、恒速率左转模型及恒速率右转模型.三个模型之间的交互主要体现在不同的模型分别匹配目标的不同运动状态,模型间的转换为一个马尔可夫过程,模型间的转移概率是一个马尔可夫链,最终的滤波结果为各个模型的滤波估计的加权和.可以看出,当目标发生机动时,通过模型的切换可实现对其跟踪滤波.
3.1 交互多模型
交互多模型的思想[20]是用不同的模型来匹配目标不同的运动状态,不同模型间的转移概率是一个马尔科夫链,目标状态的总计估计是各个模型的状态估计值的加权和.交互多模型的原理如图1所示.
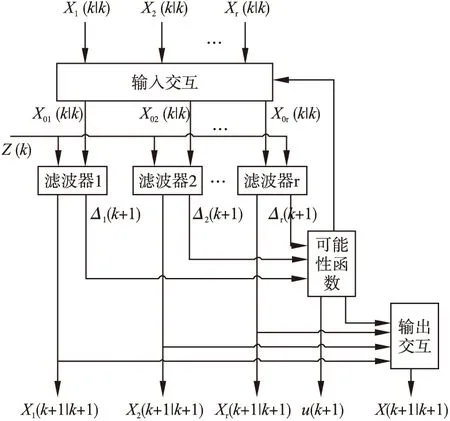
图1 交互多模型原理Fig.1 Interacting multiple model theory
从图1可以看出,交互多模型算法步骤为:1)交互输入估计;2)各模型滤波;3)模型概率更新;4)输出交互.交互多模型主要是通过并行处理多个模型下的目标跟踪并计算该模型当前概率,最后按模型的概率权重对各模型下的估计结果进行融合.
3.2 IMM-ET-GMPHD滤波递推
假设任意时刻每个模型下的ET-GMPHD包含相同数量的高斯分量,且每个模型的每个高斯分量具有一一对应关系,分别计算每个模型下ET-GMPHD以及每个高斯分量模型的条件概率,最终将ET-PHD得到的滤波结果进行融合,这样可以建立具有封闭解的IMM-ET-GMPHD算法的递归模型.提出的IMM-ET-GMPHD算法具体步骤为:
步骤1.模型条件初始化.
计算扩展多目标状态随机集合的混合转移概率
(5)
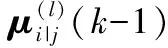
(6)
pij为模型i到模型j的先验转移概率.
步骤2.输入交互和滤波估计.根据上一步得到模型混合概率进行交互,即:输入值为各模型得到的值与模型混合概率的加权和.
状态估计为:
(7)
协方差估计为:
(8)
步骤3.各模型滤波.这里本文采用了三个经典模型分别为匀速模型、恒速率左转模型以及恒速率右转模型,各模型都采用ET-GMPHD滤波算法,根据得到的交互状态以及协方差,利用划分的量测进行更新,求得相应的状态估计及误差协方差.
1)条件PHD预测.多机动扩展目标PHD预测步骤类似于点目标的PHD预测,假设k-1时刻扩展目标的PHD函数为vk-1(xaug),则k时刻,目标状态的PHD预测函数为:
vk|k-1(xaug)=γk(xaug) +vS,k|k-1(xaug)
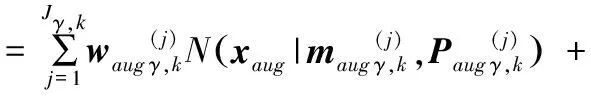
(9)
其中,γk(xaug)表示新生目标集的强度函数,vS,k|k-1(xaug)表示存活目标集的强度函数,每个高斯分量的状态预测均值和协方差可通过卡尔曼滤波[21]进行计算.
2)条件PHD更新.设k时刻的预测PHD函数满足高斯混合分布即:
(10)
则k时刻更新PHD函数为:
(11)
该函数主要包含两部分,漏检更新以及量测更新.漏检更新处理为:
(12)
量测更新为:
(13)
(14)
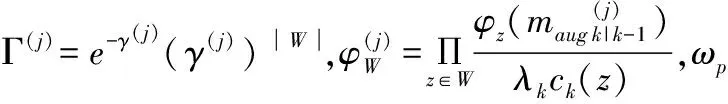
步骤4.低概率高斯的分量的删减.这一步非常关键,这里因为扩展目标的量测为泊松分布,在量测更新时各个模型都产生了大量的高斯分量,因此在交互输出前,我们先删除在各模型中概率很低的高斯分量.即:
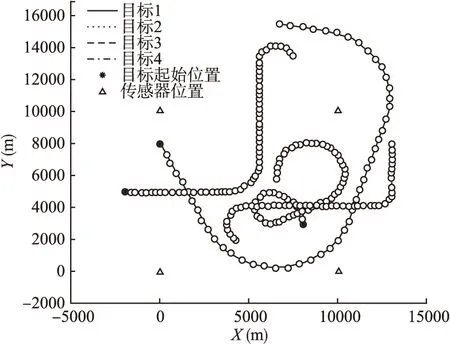
ifw{1}(j) deletexfilter(j) 上述式中w{1}(j)表示第1个模型中第j个高斯分量的概率,Td为修剪阈值. 步骤5.模型概率更新.首先计算量测的似然函数: (15) 模型的概率更新为: (16) 步骤6.交互输出.根据各模型的滤波值进行加权求和输出.即: 目标状态输出: (17) 协方差输出: (18) 步骤7.高斯分量修剪与合并.由于滤波算法更新步骤产生大量的高斯分量,为了保持一个合理的高斯分量数,降低计算代价,需对高斯分量进行修剪与合并.设τ为剪枝阈值,Jmax为允许的最大高斯分量数.对更新得到的Jk个高斯分量进行剪枝,即对小于剪枝阈值得到高斯分量直接删除,同时删除对应标签.此外,设置一个合并阈值U,当高斯分量由于彼此接近程度达到该阈值时,对这些高斯分量进行合并处理,同时对其对应标签进行处理. 步骤8.目标状态估计.目标的数目估计是通过融合后PHD的各高斯分量的权值求和取整得到,目标的状态估计则是根据给出的权值门限Thead[11],提取出权值大于门限的高斯分量及对应标签. 基于概率假设密度滤波器的多目标跟踪算法虽然可以避免在复杂数据关联[22]的情况下实现对未知数目的多目标进行跟踪,但无法获得各个目标的完整航迹,从而给一些后续处理,如目标行为识别、身份识别等带来困难.因此,文中进一步提出一种高斯分量标识方法来实现对多机动扩展目标的航迹进行管理,高斯分量标识方法可以通过树形结构的概念来解释. (19) 图2 高斯分量标识法Fig.2 Gaussian component labeling method 1)初始化.在k时刻,给每一个高斯分量分配标识,即: 2)预测.串联新生目标标签和预测标签构造新的集合: 3)更新.对于每一个更新的高斯分量分配与其前一时刻相同的标签,即保持标签的一致性,对于同一目标来说所有的高斯分量都分配到了相同的标签.并计算其权重函数W. 4)修剪与合并.对于小于剪枝阈值的高斯分量删除的同时,删除对应的标签,对分布接近的高斯分量合并时,新的高斯分量的标签与合并的高斯分量的标签相同. 5)航迹估计.筛选出最大权重的高斯分量的标签,即为跟踪目标的标签. 扩展目标的生存概率和检测概率分别为PS=0.99和PD=0.99,状态向量方差为: Q=B×diag([sigma_a2sigma_a^2])×BT, 量测向量的方差为:R=diag([sigma_ex2sigma_ex2]). 其中,sigma_ex=5.杂波量测数目服从均值为50/((xMax-xMin)×(yMax-yMin))的泊松分布,在监控区域均匀分布.这里的xMax,xMin,yMax,yMin分别表示监控区域的边缘值.每个扩展目标每一时刻产生量测的个数服从均值为10的泊松分布.高斯分量的剪枝阈值τ=1×e-4,合并阈值U=4. 交互的多模型主要是采用了经典的三个模型:匀速运动模型、恒速率左转模型和恒速率右转模型. 匀速运动模型: 恒速率左转模型: 右转弯模型: 场景设定为:目标1的初始状态为[-2000,5,5000,0,0],第1~20s做匀速直线运动,第21~30s做角速度为ω=9π/10800的左转弯运动,第31~50s做匀速直线运动,第51~60s做角速度ω=18π/10800的右转弯运动;目标2的初始状态为[1300,0,8000,-5,0],第1~10s做匀速直线运动,第11~15s做角速度ω=18π/10800的右转弯,第16~40s做匀速直线运动,第41~50s做角速度ω=15π/10800的左转弯运动;目标3初始状态[8000,0,3000,5,0],第1~10 s做角速度为ω=9π/10800的左转弯运动,第11~ 22s做角速度为ω=18π/10800的左转弯运动,第23~32s做匀速直线运动,第33~50s做角速度ω=9π/10800的右转弯运动,第51~60s做匀速直线运动;目标4初始状态[0,5,8000,-10,0],第11~20 s做匀速直线运动,第21~ 35s做角速度为ω=9π/10800的左转弯运动,第36~45s做匀速直线运动,第46~56s做角速度ω=18π/10800的右转弯运动,第57~60s做匀速直线运动. 在上述设置的场景下分别对原始ET-GMPHD算法和提出的IMM-ET-GMPHD算法进行了仿真实验,并进行了对比分析,主要从复杂环境下的跟踪效果,100次蒙特卡洛实验的平均OSPA距离以及平均目标数这三个方面进行了分析.图3-7为得到的仿真实验结果,图3和图4分别为提出的IMM-ET-GMPHD算法和原始ET-GMPHD算法对多机动扩展目标位置的估计结果,图中圆圈对应的是根据滤波算法得到的位置估计结果,可以看出当目标发生机动时,原始的ET-GMPHD算法对目标的跟踪性能明显下降,甚至出现跟踪不上的情况,而IMM-ET-GMPHD算法对多机动扩展目标具有良好的跟踪性能. 图3 IMM-ET-GMPHD滤波估计Fig.3 IMM-ET-GMPHD filter estimation 图4 ET-GMPHD滤波估计Fig.4 ET-GMPHD filter estimation 图5是100次蒙特卡洛仿真实验的IMM-ET-GMPHD算法和原始ET-GMPHD算法对每一时刻目标数估计的平均结果与目标真实数对比,可以看出当目标发生机动时原算法的目标数估计出现漏估情况,而提出的算法能够很好地估计多机动扩展目标的目标数. 图6所示为经过100次Monte Carlo仿真实验,提出的IMM-ET-GMPHD算法和原始ET-GMPHD算法的OSPA距离均值对比.从OSPA距离的对比可以看出,当目标发生机动,即转弯时(对应图中21s以及36s)原始ET-GMPHD算法跟踪不上OSPA距离急剧增大,而提出的IMM-ET-GMPHD算法的OSPA距离比较平稳,说明其对多机动扩展目标跟踪具有更高的精度. 图5 目标数估计Fig.5 Number of target estimation 图7所示为每个多机动扩展目标的航迹管理,图中实线表示每个机动扩展目标的x方向和y方向的真实轨迹,另外,通过IMM-ET-GMPHD的高斯分量标识方法得到了每个多机动扩展目标的航迹,在图中分别用*,△,□,◇表示,可以看出提出的IMM-ET-GMPHD高斯分量表标识方法在每一时刻能够有效地估计各个机动扩展目标的航迹,实现对多机动扩展目标的航迹管理. 图6 OSPA距离Fig.6 OSPA Distance 图7 IMM-ET-GMPHD航迹管理Fig.7 IMM-ET-GMPHD track management 从上述仿真结果分析不难看出本文提出的IMM-ET-GMPHD算法能够对多杂波环境下的多机动扩展目标的状态和目标数进行准确估计,实现对多机动扩展目标的跟踪.但由于需对多个模型进行处理,增加了时间复杂度,对此,本文做了进一步的研究,在同等条件下,原始扩展目标跟踪算法所需的运行时间为340.231s,而本文提出的方法则需989.393s,可以看出,本文的方法在牺牲一定时间复杂度的基础上提升了对多扩展机动目标跟踪的精度. 本文针对传统的ET-GMPHD跟踪算法不能有效解决扩展目标的机动问题,引入交互多模型的思想,提出了IMM-ET-GMPHD算法.该算法主要融合了三个经典模型,通过三个模型的交互实现了对复杂场景下多机动扩展目标的跟踪.同时为了解决扩展多目标跟踪算法下无法获取各个目标的完整航迹问题,本文在所提出的算法基础上引入高斯分量标识的方法,实现了对多机动扩展目标的航迹管理,仿真结果表明,本文提出的算法对于多机动扩展目标的跟踪具有更高的准确性和鲁棒性. [1] Baum M,Hanebeck U D.Random hypersurface models for extended object tracking[C].IEEE International Symposium on Signal Processing and Information Technology,2009:178-183. [2] Mahler R.PHD filters for nonstandard targets,I:extended targets[C].12th International Conference on Information Fusion,2009:915-921. [3] Lian Feng,Han Chong-zhao,Liu Wei-feng.Convergence analysis of the Gaussian mixture extended-target probability hypothesis density filter[J].Acta Automatica Sinica,2012,38(8):1343-1352. [4] Beard M,Reuter S,Granstrom K,et al.Multiple extended target tracking with labeled random finite sets[J].IEEE Transactions on Signal Processing,2016,64(7):1638-1653. [5] Wahlstrom N,Ozkan E.Extended target tracking using Gaussian processes[J].IEEE Transactions on Signal Processing,2015,63(16):4165-4178. [6] Mahler R.PHD filters of higher order in target number[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(4):1523-1543. [7] Mahler R P S.Multitarget Bayes filtering via first-order multitarget moments[J].IEEE Transaction on Aerospace and Electronic Systems,2003,39(4):1152-1178. [8] Hauschildt D.Gaussian mixture implementation of the cardinalized probability hypothesis density filter for superpositional sensors[C].International Conference on Indoor Positioning and Navigation,2011:1-8. [9] Pasha S A,Vo B N,Tuan H D.A Gaussian mixture PHD filter for jump Markov system models[J].IEEE Transactions on Aerospace & Electronic Systems,2009,45(3):919-936. [10] Angelova D,Mihaylova L.Extended object tracking using Monte Carlo methods[J].IEEE Transactions on Signal Processing,2008,56(2):825-832. [11] Vo B N,Ma W K.The Gaussian mixture probability hypothesis density filter[J].IEEE Transaction on Signal Processing,2010,54(11):4091-4104. [12] Gilholm K,Godsill S,Maskell S,et al.Poisson models for extended target and group tracking[C].Signal and Data Processing of Small Target,2005:230-241. [13] Granström K,Lundquist C,Orguner O.A Gaussian mixture PHD filter for extended target tracking[C].13th International Conference on Information Fusion,2010:1-8. [14] Blom H A P,Bar-Shalom Y.The interacting multiple model algorithm for systems with Markovian switching coefficients[J].IEEE Transactions on Automatic Control,1988,33(8):780-783. [15] Jilkov V P,Angelova D S,Semerdjiev T A.Design and comparison of mode-set adaptive IMM algorithms for maneuvering target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(1):343-350. [16] Johnston L A,Krishnamurthy V.An improvement to the interacting multiple model(IMM) algorithm[J].IEEE Transactions on Signal Processing,2001,49(12):2909-2923. [17] Li X R,Bar-Shalom Y.Multiple-model estimation with variable structure[J].IEEE Transactions on Automatic Control,1996,41(4):478-493. [18] Mazor E,Averbuch A,Bar-Shalom Y,et al.Interacting multiple models in target tracking:a survey[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):103-123. [19] Li X R,Jilkov V P.Survey of maneuvering target tracking.Part V.multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1255-1321. [20] Ho T J.A switched IMM-extended viterbi estimator- based algorithm for maneuvering target tracking[J].Automatica,2011,47(1):92-98. [21] Long Hui,Fan Xiao-ping,Liu Shao-qiang.Research on scalable consensus algorithm of target tracking for wireless sensor network[J].Journal of Chinese Computer Systems,2012,33(11):2429-2434. [22] Panta K,Clark D E,Vo B N.Data association and track management for the Gaussian mixture probability hypothesis density filter[J].IEEE Transaction on Aerospace & Electronic Systems,2009,45(3):1003-1016. 附中文参考文献: [3] 连 峰,韩崇昭,刘伟峰.高斯混合扩展目标概率假设密度滤波器的收敛性分析[J].自动化学报,2012,38(8):1343-1352. [21] 龙 慧,樊晓平,刘少强.无线传感器网络可扩展一致性目标跟踪算法研究[J].小型微型计算机系统,2012,33(11):2429-2434.

3.3 航迹维持
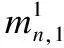
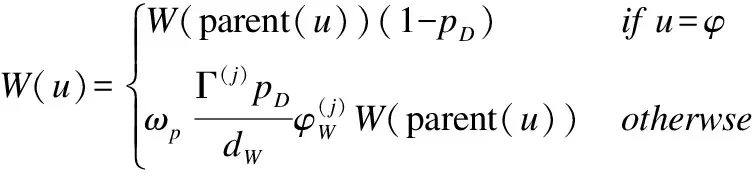



4 实验结果与分析
4.1 仿真场景设置
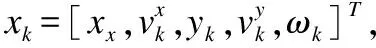

4.2 仿真结果分析




5 结束语

