公平交换协议的信道可信度形式化验证方法

杨晋吉,申涵瑞,陈清亮

1(华南师范大学 计算机学院,广州 510631) 2(暨南大学 计算机科学系,广州 510632)

1 引 言

随着电子商务技术的发展,越来越多的电子商务应用进入人们日常生活,电子商务的安全性问题也变得更加重要.公平交换协议作为一种重要的电子商务安全协议,在保障电子商务应用的安全性方面扮演了非常重要的角色.公平性、有效性和时限性是电子商务安全的核心属性,设计出公平安全的公平交换协议是电子商务发展的迫切要求,针对公平交换协议进行分析验证具有十分重要的意义.但由于公平交换协议的复杂性,公平交换协议的形式化验证领域仍存在许多问题,例如简易有效的针对安全属性的分析方法和符合现代工业要求的公平交换协议等.

信道问题是公平交换协议分析中一个重要问题.在开放的网络环境下,消息在信道传输的过程中会由于信道错误或恶意实体的主动攻击,导致消息的丢失、错误或延迟[1].因此基于信道可信度对公平交换协议的核心属性进行定量分析在实际工程中具有重要的作用.

目前国内外已有很多关于公平交换协议的研究.文献[2]对Ray协议进行安全性分析,验证该协议为一个使用在线可信第三方的公平交换协议.文献[3]基于交替时态逻辑对公平交换协议的安全属性进行了定性分析.文献[4]证明了Ben-Or等协议存在针对协议参与者的攻击策略,并分析了攻击者的成功概率和需要的信息时延.

形式化验证是对公平交换协议进行分析的重要方法.文献[5]基于线性时态逻辑,使用模型检测工具SPIN对普通文件传输协议进行建模和验证.文献[6]使用归纳法对不可否认性协议进行了分析.文献[7]使用工具PRISM对分布式实时操作系统任务的可调度性问题进行了量化分析.

目前关于公平交换协议的许多形式化方法目的是发现更多的攻击路径,定性判断协议是否满足给定性质.为了分析信道环境对协议执行的影响,本文提出了基于信道可信度对公平交换协议进行形式化验证的方法,重点对公平交换协议中的信道问题进行定量分析.

本文第2节介绍了概率模型检测相关的基本理论,给出本文使用的概率模型检测框架,第3节基于信道可信度对公平交换协议进行了形式化验证,使用PRISM模型检测工具对协议进行建模并对协议核心属性进行定量分析,最后对全文进行总结.

2 概率模型检测

自从20世纪80年代起,模型检测(modelchecking)[8,9]已经成为了一项验证计算机系统各项性质的重要技术.通过给定计算机系统的形式化模型和描述计算机系统性质的时序逻辑命题,模型检测技术可以实现自动化验证该计算机系统是否满足给定的性质.模型检测工具可以通过遍历计算机系统的所有相关状态来确定计算机系统是否满足所给性质.

随着计算机系日趋庞大和复杂,很多实际的系统被赋予随机行为特征[9,10].这样的系统可以通过对状态之间的转换概率进行建模.概率模型包括离散时间马尔可夫链(discrete-time Markov Chain,DTMC)、连续时间马尔科夫链(continuous-time Markov Chain,CTMC)和马尔可夫决策过程(Markov decision processes,MDP)等.通过概率模型描述具体的计算机系统,用模型检测的方法对随机系统进行自动化的形式验证,定量分析系统满足用户的功能或非功能需求性质的程度,即概率模型检测(probabilistic modelchecking).

本文通过离散时间马尔可夫链对公平交换协议进行形式化建模,然后通过概率计算树逻辑对公平交换协议的核心属性进行定量分析.

2.1 离散时间马尔可夫链

离散时间马尔可夫链(discrete-time Markov Chain,DTMC)是最常见的概率模型.

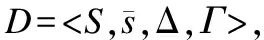
S是有限状态集;

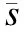
Δ:S×S→[0,1]是迁移概率函数;

Γ:S→2AP是标记函数.

图1是一个离散时间马尔可夫链的实例.

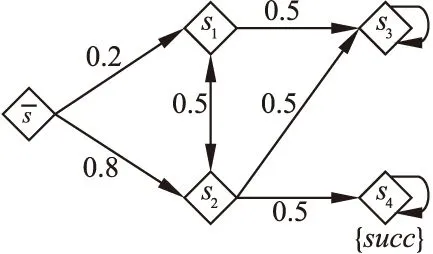
图1 离散时间马尔可夫链实例Fig.1 A simple DTMC

2.2 概率计算树逻辑

概率计算树逻辑(Probabilistic Computation Tree Logic,PCTL)由Hansson和Jonsson最先提出,是一个对计算树逻辑(Computation Tree Logic,CTL)的概率扩展,用概率运算符P～p定量地扩展了计算树逻辑的路径量词A(all)和E(exists),能够描述概率模型的定量属性.

定义2.关于原子命题集合AP的PCTL状态公式Φ可定义为Φ∷=true|a|Φ∧Φ|Φ|P～p(Ψ),路径公式Ψ可定义为Ψ∷=XΦ|ΦUΦ|ΦU≤nΦ,其中:

a∈AP,是原子命题;

X(next)表示下一状态;

U(until)表示直到某状态;

U≤n是U的变体,要求n次迁移或小于n次迁移内满足U的语义;

～∈{≤,<,≥,>};

p∈[0,1]是概率界限值.

以图1所示的离散时间马尔可夫链为例,可以描述其最终达到成功状态的概率.

P=[Fsucc]

可以通过集合S中各状态的迁移概率值求解上述公式.

xs1=0.5·xs2+0.5·xs3

xs2=0.5·xs3+0.5·xs4

xs3=0

xs4=1

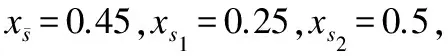
P=[Fsucc]=0.45

3 基于信道可信度的概率模型检测

本文提出基于信道可信度对公平交换协议的核心属性进行定量分析.为了实现定量分析公平交换协议的核心属性,本文首先针对公平交换协议的实体分别进行了形式化建模,在建模过程中设计信道可信度对协议的影响,然后基于信道可信度定量分析公平交换协议的核心属性.

3.1 公平交换协议形式化建模

公平交换协议(Fair Exchange Protocols)是使用最为广泛的电子商务协议,本文选用了一个电子合同签署协议(Contract Signing Protocols)[11]为例,对其进行形式化建模与验证.协议实体主要包含参与者A、参与者B与可信第三方(Trusty Third Party,TTP),通过对协议实体进行建模可以分析协议是否满足公平交换协议的主要安全属性:公平性(Fairness)、有效性(Effectiveness)和时限性(Timeliness).在电子合同签署的过程中,参与者之间难免会出现争端的情况,因此,一个完备的电子合同签署协议通常需要有一个主协议和一个争端解决协议.主协议用来处理普通的电子合同签署过程,争端解决协议用来处理在电子合同签署过程中出现的争端.

为了实现对公平交换协议的核心属性进行自动化验证,本文使用模型检测工具PRISM[12]对选用的电子合同签署协议进行形式化建模.首先通过离散时间马尔可夫链对协议的主协议和争端解决协议进行描述.

电子合同签署协议的主协议及争端解决协议分别为:

1)电子合同签署协议的主协议:

Step1.A→B:MSG1=SIGA(IDB,C,ETTP(IDA,RA))

Step2.B→A:MSF2=SIGB(IDA,MSG1,ETTP(RB))

Step3.A→B:MSG3=RA

Step4.B→A:MSG4=RB

其中,IDA为A的ID信息,C为合同内容,ETTP为加密后的信息,RA为A的密钥.

表1 符号表示
Table 1 Symbols′ expression

符 号含 义SendMessagei二值变量，false表示消息i未被发送，true表示消息i已被发送．checkMessagei变量，0表示消息i未检验，1表示消息i通过检验，2表示消息i未能通过检验．stopX二值变量，false表示模块X正常运行，true表示模块X选择终止协议reliabilityAB参与者A与参与者B间信道可信度reliabilityTTP参与者A、B与TTP间信道可信度

每一步的信息接收方在接收信息后,通过检查信息是否完备选择下一步操作.例如,在第二步时,当B收到A发送的消息1后,先检查消息1是否完备.如果消息1完备,那么B向A发送消息2,消息2中包含A的ID信息、消息1、加密后B的密钥以及B的签名;如果消息1不完备,那么B选择终止协议.

[] !stopB & sendMessage1 & (checkMessage1=0) & !sendMessage2->reliabilityAB:(checkMessage1′=1)+(1-reliabilityAB):(checkMessage1′=2);

[] !stopB & sendMessage1 & (checkMessage1=2) & !sendMessage2->1:(stopB′=true);

[] !stopB & sendMessage1 & (checkMessage1=1) & !sendMessage2->1:(sendMessage2′=true);

2)争端解决协议:

Step5.A,B→TTP:MSG5=msg1+msg2

msg1=SIGA(IDB,C,ETTP(IDA,RA))

msg2=SIGB(IDA,MSG1,ETTP(RB))

Step6.TTP→A:MSG6=MSG2,RB

Step7.TTP→B:MSG7=MSG1,RA

TTP初始状态为终止状态,当协议出现争端的情况时,由A或B发起争端解决协议.当TTP收到消息5后,先检查消息5是否完备.如果消息5完备,那么TTP就会把消息6发送给A,把消息7发送给B.其中,消息6包含B的密钥,消息7包含A的密钥.如果消息5不完备,那么TTP选择终止协议.

[] stopTTP & sendMessage5B & (checkMessage5B=0)->1:(stopTTP′=false);

[] stopTTP & !sendMessage5B & sendMessage5A & (checkMessage5A=0)->1:(stopTTP′=false);

[] !stopTTP & sendMessage5B & (checkMessage5B=0)->reliabilityTTP:(checkMessage5B′=1)+(1-reliabilityTTP):(checkMessage5B′=2);

……

[] !stopTTP & !sendMessage5B & sendMessage5A & (checkMessage5A=0)->reliabilityTTP:(checkMessage5A′=1)+(1-reliabilityTTP):(checkMessage5A′=2);

图2 电子合同签署协议模型Fig.2 Model of contract signing protocols

3.2 协议性质验证和分析

目前国内外已有很多针对公平交换协议进行定性分析的研究,但随着现代工业的发展,实际项目对相关数据有了进一步的要求,因此本文对公平交换协议的公平性、有效性和时限性进行了定量分析.

公平性(Fairness)保证了电子合同签署协议的签署双方要么都能够获得对方签署过的合同,要么都无法获得对方签署过的合同.因此如果电子合同签署协议满足公平性,那么系统不存在这样的状态:在协议结束的时候,只有A签署了合同,而B没有签署合同.因此可以把协议不满足公平性描述为:

label "unfair"=stopA & stopB & stopTTP & ((sendMessage3 & checkMessage3=1) | sendMessage7) & ((sendMessage4 & checkMessage4=2) | (!sendMessage4 & !sendMessage6))

其中,stopA & stopB & stopTTP是协议结束的标志;sendMessage3 & checkMessage3=1和sendMessage7是A签署合同的两种情况;sendMessage4 & checkMessage4=2和!sendMessage4 & !sendMessage6是B没有签署合同的两种情况.

通过定义reliabilityAB和reliabilityTTP可以描述参与者A、B和TTP之间的信道可信度.假设参与者A、B间信道可信度为0.8.首先验证当参与者A、B与TTP间的信道可信度为0.8时,电子合同签署协议是否满足公平性,因此将reliabilityAB和reliabilityTTP都设置为0.8.

当使用PRISM验证模型属性时,默认情况下,将返回模型初始状态的值.但由于实际需要,可以通过设置filters过滤器同时计算模型所有状态的值.通过PRISM计算协议不满足公平性的状态概率可以描述为:

filter(state,P=? [ F "unfair" ],"init")

检验属性,得到结果:0.08192.同理,通过设置reliabilityAB,得到当参与者A、B与TTP信道可信度为0.8时,参与者A与参与者B信道可信度取不同值条件下协议不满足公平性的状态概率.

检验结果如图所示,横轴代表参与者A、B间信道可信度,纵轴代表协议不满足公平性的状态概率.由检验结果可以得出,只有当reliabilityAB取值为0或1时,协议不满足公平性概率为0,即协议满足公平性;当reliabilityAB取值为0.7时,协议不满足公平性的概率接近最大值,为0.08232.

图3 协议不满足公平性的概率Fig.3 Probability that the protocol does not satisfy the fairness

在传统安全协议中,通常假设协议在不安全的信道上进行,所有在信道上传输的消息都有可能被拦截或篡改.而在公平交换协议中,如果协议只在不可靠信道上进行,发往 TTP的消息可能丢失,这就等同于没有TTP[11].因此本文针对TTP的信道可信度进行了验证分析.首先验证当TTP的信道可信度为1时,电子合同签署协议是否满足公平性.

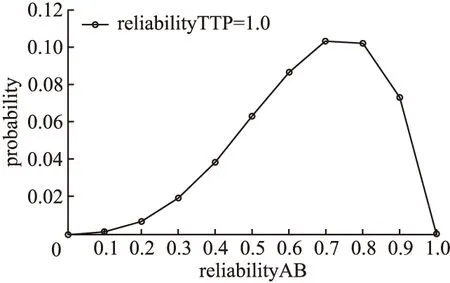
图4 协议不满足公平性的概率Fig.4 Probability of the protocol does not satisfy the fairness

通过设置reliabilityAB得到在不同信道可信度的条件下协议不满足公平性的状态概率.由检验结果可以得出,当reliabilityAB取值为0.7时,协议不满足公平性的概率接近最大值,为0.10290.相较于reliabilityTTP取值为0.8时概率更大.

图5 协议不满足公平性的概率Fig.5 Probability of the protocol does not satisfy the fairness

通过同时为reliabilityTTP和reliabilityAB设置不同值,得到协议不满足公平性的概率与信道可信度的变化关系.

有效性(Effectiveness)保证了电子合同签署协议的签署双方在满足协议设计者所设定的通信信道质量,并且签署双方都诚实的条件下,协议签署双方都能获得对方签署过的合同.Kremer依据强度不同定义了两种有效性[13]:弱有效性和强有效性.弱有效性是在排除了协议签署主体不诚实和信道质量不可靠这两项不利因素后,协议应当满足的属性.强有效性是在排除协议签署主体不诚实这项不利因素后,协议应当满足的属性.因此可以把协议满足有效性描述为:

label "effective"=stopA & stopB & stopTTP & ((sendMessage3 & checkMessage3=1) | sendMessage7) & ((sendMessage4 & checkMessage4=1) | sendMessage6)

首先验证协议是否满足弱有效性,将reliabilityAB和reliabilityTTP都设置为1,得到协议满足若有效性的概率为1.因此可以判定协议满足弱有效性.

然后验证协议是否满足强有效性,通过为reliabilityAB和reliabilityTTP设置不同值,得到当A、B与TTP间信道可信度为不同值时,协议满足强有效性的概率.

图6 协议满足强有效性的概率Fig.6 Probability of the protocol satisfy the strong effectiveness

由检验结果可知,协议满足强有效性的概率随reliabilityAB取值增大而增大;当reliabilityAB为0时,概率为0;当reliabilityAB取值为1时,概率为1.协议是否满足强有效性与参与者A、B与TTP间信道可信度取值无关.

时限性(Timeliness)保证了电子合同签署协议能够在A提出终止协议执行后,能够及时有效的终止协议.如果此时A已经获得了B签署的合同,那么电子合同签署协议应该在B也获得A签署的合同之后终止协议.如果此时A还没有获得B签署的合同,那么电子合同签署应该保证在协议结束时,B也没有获得A签署的合同.因此如果电子合同签署协议满足及时性,那么系统不存在这样的状态:当A请求终止协议时,如果此时B还没有签署合同,那么系统在未来的某个状态中出现了A签署了合同而B没有签署合同的状态.因此可以把协议不满足及时性描述为:

label "untimely"=(stopA & ((!sendMessage4 & !sendMessage6) | (sendMessage4 & checkMessage4=2))) => (stopA & stopB & stopTTP & ((sendMessage3 & checkMessage3=1) | sendMessage7) & ((!sendMessage4 & !sendMessage6) | (sendMessage4 & checkMessage4=2)))

通过为reliabilityAB和reliabilityTTP设置不同值,得到当A、B与TTP信道可信度为不同值时,协议不满足时限性的状态概率.

由检验结果可知,只有当reliabilityAB取值为0或1时,协议不满足公平性概率为1;当reliabilityAB取值为0.7时,协议不满足时限性的概率接近最小值,为0.75.协议是否满足时限性与参与者A、B与TTP间信道可信度取值无关.

综上所述,电子合同签署协议满足核心属性的概率随信道可信度的变化而变化.其中,协议满足公平性的概率随参与者A、B和TTP间的信道可信度增大而减小,协议满足有效性和时限性的概率与参与者A、B和TTP间的信道可信度无关;协议满足公平性、有效性和时限性的概率随参与者A和参与者B间的信道可信度变化而变化,当信道可信度取0.7时协议满足公平性概率接近最小为0.89710,协议满足有效性的概率随信道可信度的增大而增大,当信道可信度取0.7时协议满足时限性概率接近最大为0.25.由检验结果可知,协议各实体间信道可信度对协议的公平性、有效性和时限性有不同程度的影响,因此对相应信道进行控制或改善,可以提高协议的安全性.

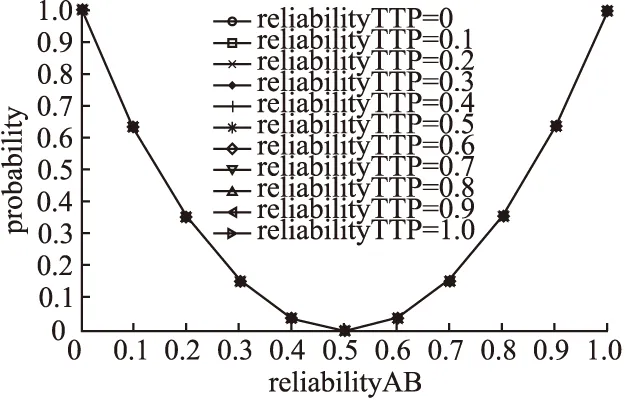
图7 协议不满足时限性的概率Fig.7 Probability of the protocol does not satisfy the timeliness

4 总 结

本文提出基于信道可信度对公平交换协议的核心属性进行定量分析,运用概率模型检测的形式化验证方法,以一个电子合同签署协议为例,对公平交换协议的核心属性进行分析验证.首先基于离散时间马尔可夫链对协议参与者A、B和TTP进行抽象建模,然后8在协议进行的过程中,添加了信道可信度对协议进程的影响,在状态迁移中加入了信道可信度,最后针对公平交换协议的核心属性进行定量分析.本文对公平交换协议的公平性、有效性和时限性等核心属性进行了量化分析,利用检验结果,可以对应用环境进行具体分析,对相应信道进行控制或改善,使得概率在可控的范围内,提高协议的安全性.同时将不同信道可信度条件下协议满足核心属性的概率在同一坐标下进行对比,可以使设计人员做出更直观的判断,有利于对系统的设计.定量形式化分析结果可以为开发人员提供参考依据,进一步增加系统的可靠性和正确性,此方法同样适用于其他安全协议.在下一步的研究中可以将此方法推广应用于其他安全协议及分布式系统的形式化验证等领域.

[1] Asokan N.Fairness in electronic commerce[M].University of Waterloo,1998.

[2] Xu Jing-fang,Cui Guo-hua,Cheng Qi,et al.Security analysis and improvement of fair exchange protocols using the theory of cross validation[J].Journal of Chinese Computer Systems,2009,30(2):

345-348.

[3] Li Qun,Chen Qing-liang.Formal verification of fair exchange protocols based on alternating-time temporal logic[J].Computer Engineering and Applications,2015,51(19):32-36.

[4] Norman G,Shmatikov V.Analysis of probabilistic contract signing[C].Formal Aspects of Security,First International Conference,FASec 2002,London,UK,DBLP,2002:81-96.

[5] Alrabaee S,Bataineh A,Khasawneh F A,et al.Using model checking for trivial file transfer protocol validation[C].Fourth International Conference on Communications and Networking,2014:1-7.

[6] Bella G,Paulson L C.Accountability protocols:formalized and verified[J].Acm Transactions on Information & System Security,2006,9(2):138-161.

[7] Huo Yan-yan,Guan Yong,Li Xiao-juan,et al.Formal verification of distributed real-time operating system task scheduling based on PRISM[J].Journal of Chinese Computer Systems,2015,36(9):2125-2129.

[8] Clarke E M,Emerson E A.Design and synthesis of synchronization skeletons using branching time temporal logic[C].DBLP,2008:196-215.

[9] Baier C,Katoen J P.Principles of model checking (representation and mind series)[M].The MIT Press,2008.

[10] Liu Yang,Li Xuan-dong,Ma Yan,et al.Survey for stochastic model checking[J].Chinese Journal of Computers,2015,38(11):2145-2162.

[11] Wang Zhi-ling,Zhang Yu-qing,Yang Bo.Design of a fair contract signing protocol[J].Computer Engineering,2006,32(19):159-161.

[12] Kwiatkowska M,Norman G,Parker D.PRISM 4.0:verification of probabilistic real-time systems[C].In Ganesh Gopalakrishnan,Shaz Qocleer,Computer Aided Verification,Proceeding of 23rd International Conference,CAV2011,Snowbird,UT,USA,2011:585-591.

[13] Kremer S.Formal analysis of optimistic fair exchange protocols[D].Brussels:Université Libre de Bruxelles,2004.

附中文参考文献：

[2] 许静芳,崔国华,程 琦,等.关于公平交换协议中使用正交验证理论的安全性分析及改进[J].小型微型计算机系统,2009,30(2):345-348.

[3] 李 群,陈清亮.基于ATL的公平交换协议的形式化验证[J].计算机工程与应用,2015,51(19):32-36.

[7] 霍燕燕,关 永,李晓娟,等.基于PRISM的分布式实时操作系统任务调度的形式化验证[J].小型微型计算机系统,2015,36(9):2125-2129.

[10] 刘 阳,李宣东,马 艳,等.随机模型检验研究[J].计算机学报,2015,38(11):2145-2162.

[11] 王芷玲,张玉清,杨 波.一个公平电子合同签署协议的设计[J].计算机工程,2006,32(19):159-161.