光电稳定平台神经网络自抗扰控制方法
朱启轩, 张红刚, 高军科
(1.光电控制技术重点实验室,河南 洛阳 471000;2.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000)
0 引言
在飞机飞行过程中,光电稳定平台探测器视轴指向会受到各种扰动的干扰,影响视轴稳定精度,进而影响成像清晰度和信息获取准确性。提高扰动隔离度是提高视轴稳定精度的关键[1-2]。
传统的控制策略受到了机械谐振频率的严格限制,使得系统在扰动作用频段的增益无法得到进一步提高[3],进而限制了稳定精度的提高。为解决传统控制策略的内在矛盾提出了自抗扰控制(Active Disturbance-Rejection Control,ADRC),利用扰动补偿控制来抑制扰动影响。扩张状态观测器(Extended State Obser-ver,ESO)是自抗扰控制的核心,对系统中的“总和扰动”进行实时观测,并加以补偿,从而大幅度提高系统的扰动隔离度,提高光电平台稳定精度[4-5]。
ESO的参数整定对于扰动观测器的性能影响至关重要,通常用菲波纳奇数列、基于带宽概念的单参数化[6]等设计方法设定扩张状态观测器系数,这些方法具有较好的鲁棒性,经调整后可适应各类模型。
自适应调整参数的智能算法可以在保持系统较好的鲁棒性的同时提高自抗扰控制系统性能指标,因此受到重视,有些文献已经尝试使用类似BP神经网络整定PID的方式整定自抗扰控制器[7],但多数仅整定其中非线性控制律的两个参数[8-9]。事实上,扩张状态观测器的参数整定方法更为复杂,由于系统精确模型难以获得,目前主要依靠经验公式试凑对其进行调整,这种方法不仅费时而且难以确定最优参数,因此使用BP神经网络对其进行自适应调整对于提升ESO性能具有深远的意义。
1 自抗扰控制理论
自抗扰控制技术首先由中科院数学与系统科学研究院的韩京清研究员于20世纪80年代后期提出,其核心思想为“主动抗扰”,它最突出的特点就是把所有的外界扰动和系统“未建模动态”称为“总和扰动”,然后通过扩张状态观测器对该“总和扰动”进行实时估计,从而实现对扰动的直接前馈补偿控制,达到提高扰动隔离度的目的。
自抗扰控制器分为跟踪微分器、扩张状态观测器和非线性控制律三部分。
1.1 跟踪微分器
跟踪微分器的主要作用是根据控制目标和对象承受能力安排合适的过渡过程,解决系统的快速性和超调之间的矛盾。本文用的最速跟踪微分器为
(1)
式中:x1为指令的跟踪值;x2为指令微分的跟踪值;fhan(x1(k)-v(k),x2(k),r,h)是系统的最速控制综合函数,其具体算法为
(2)
式中:r为速度因子,r的值越大,跟踪速度越快;h为采样时间,其余均为中间变量。
1.2 扩张状态观测器
本文以带扰动的二阶非线性被控系统为研究对象,对扩张状态观测器的原理进行讨论,建立三阶离散扩张状态观测器,即
(3)
式中:βi(i=1,2,3)为待调整参数,后文将采用BP神经网络方法对该3个参数进行整定;fal(e1,αi,δi)为非线性函数,这是韩京清总结出来的扩张状态观测器非线性函数,即
(4)
通过调整合适的αi,δi可以得到合适的非线性函数,相比于线性ADRC,非线性ADRC具有更好的扰动估计和补偿能力,同时由于待调整参数增加,非线性ADRC的调整也就更为复杂。
1.3 非线性控制律设计
本文采用指令信号与观测信号相结合的方式生成控制律,类似于PD控制,采用的非线性控制律为
u0=k1·fal(e1,α3,δ3)+k2·fal(e2,α4,δ4)
(5)

2 基于BP神经网络的ADRC参数整定方法
2.1 基于BP神经网络的ESO参数整定方法结构
ESO的参数整定是自抗扰控制器设计的重要环节,由于自抗扰控制不依赖系统精确模型的特点,ESO参数的选择往往采用经验公式的调整方法,利用BP神经网络在线整定ESO参数,可以使ESO随扰动变化及系统自身变化而进行自适应参数调整,相当于进行了自动调整的系统辨识,可以在提高自抗扰控制系统鲁棒性的同时提高ESO观测值精确性,进而提高系统的稳定精度。图1所示为基于BP神经网络整定ESO参数的ADRC结构框图。
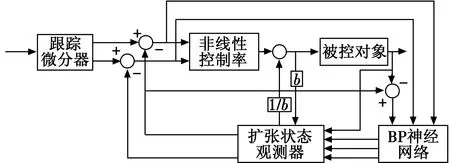
图1 BP神经网络整定的ADRC结构框图Fig.1 ADRC based on BPNN
使用基于BP神经网络整定ESO参数β1,β2,β3,方法是采用三层BP神经网络,神经网络的输入应选择与ESO观测精度关系最为密切的几个信号,经试验,选择以信号误差E1、信号微分误差E2、观测值误差eerror这3个信号和偏置值1作为神经网络的4个输入节点,隐含层节点数一般比输出层节点数稍多,输出层节点为3个ESO参数β1,β2,β3,结合特定被控对象并经过试凑选择5个隐含层节点, 由此得出图2所示的BP神经网络内部结构。
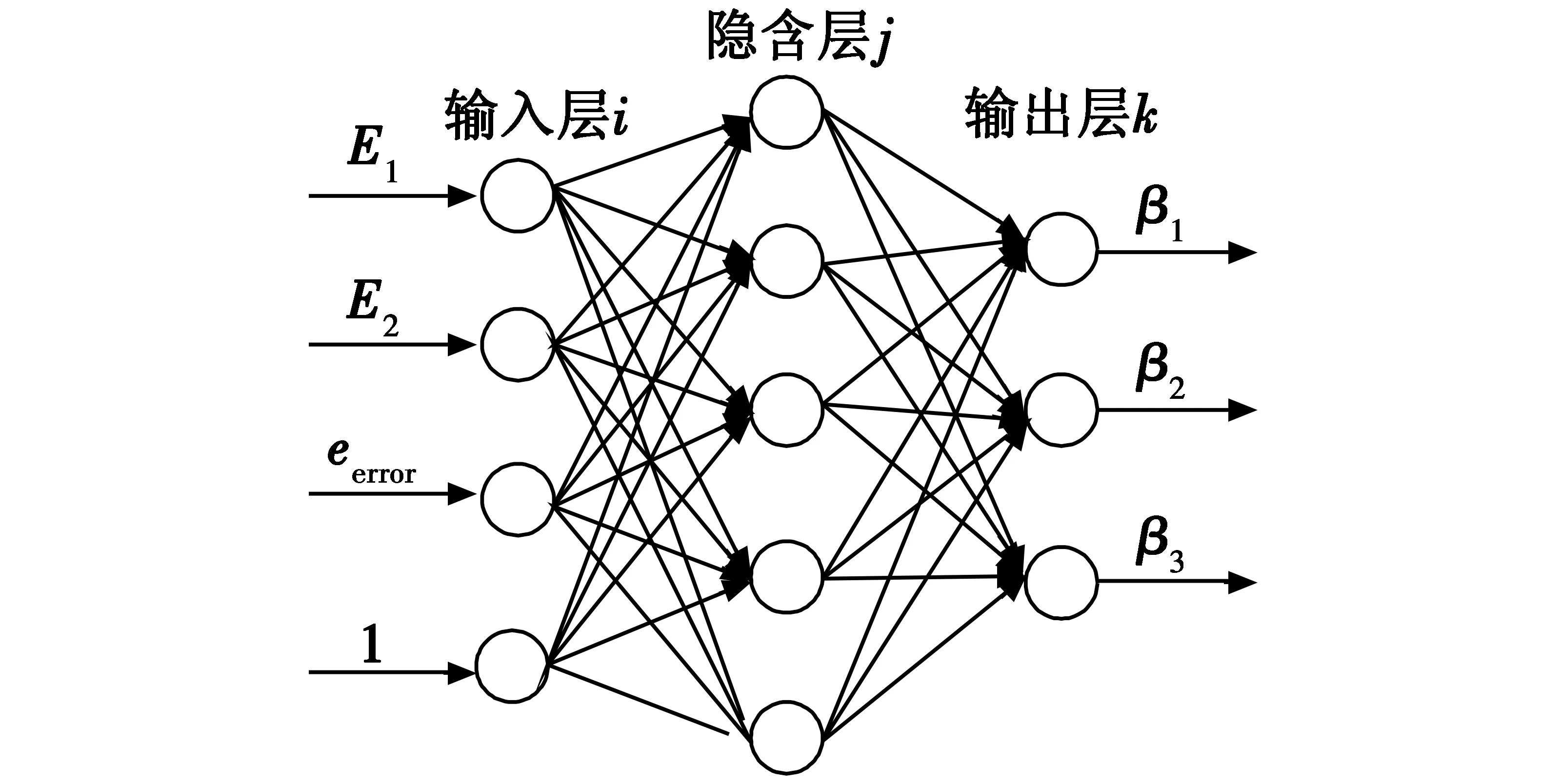
图2 BP神经网络整定的ESO内部结构图Fig.2 Internal structure of ESO based on BPNN
由于神经网络输出层的激活函数往往选择sigmoid函数,其特性是输出值非负且小于等于1,而ESO的参数并不在此范围内,因此在使用BP神经网络对ESO进行参数整定时需要对BP神经网络的输出值进行调整再作为ESO的参数使用,否则自抗扰控制器将无法收敛。由于BP神经网络是按照梯度下降法修正网络的权值系数,这种方法的缺点是如果输出值与理想输出偏差过大很容易发散,因此需要选取比较合适的输出层系数,使神经网络更好地收敛。
2.2 用于整定ESO参数的BP神经网络简述
上文确定的神经网络输入层的输出为

(6)
隐含层输入、输出分别为

(7)
隐含层神经元激活函数采用双曲正切函数

(8)
输出层的输入输出
(9)
输出层输出节点分别对应3个ESO参数β1,β2,β3,Ak为输出层系数,输出层神经元激活函数采用非负的sigmoid函数,即

(10)
定义系统的代价函数为

式中:rin()是系统的指令值;yout()是系统的输出。
BP神经网络的反向传播算法应用已经很成熟,在此不再赘述。
2.3 ESO参数迭代输出层系数选取方法
提出一种将输出层激活函数输出乘以由BP神经网络训练得出的相应输出层系数再作为ESO参数使用的方法,如图3所示。

图3 输出层系数选取方法流程图Fig.3 Flow chart of coefficient selection for output layer
首先用基于带宽概念的单参数化设计方法[6]选择一组初始系数[3ω,3ω2,ω3]的基值,其中,参数ω与系统带宽有关,ω数值越大,ESO的带宽越高。
ESO中扩张状态的收敛性和ESO参数h,β1,β2,β3密切相关[12]。由于采样间隔h受到处理器的限制,无法进一步提高,要使ESO的收敛性更好,则需要调整β1,β2,β3这3个参数,使其更加适用于被控对象。上文所述的系数选取方法通过迭代,使ESO参数从一个较优的初始值开始,在系统工作过程中神经网络会根据系统的性能再对ESO参数进行进一步的调整优化,这样的方法比传统的试凑法调整ESO参数要快捷,并且观测性能更好。
3 仿真分析
3.1 光电稳定平台构型
光电稳定平台伺服控制系统以陀螺、旋转变压器/光电编码器、图像跟踪器等作为反馈元件,通过控制器处理输入信号及反馈信号并驱动电机对平台负载进行控制。控制器通过调整PWM波信号实现对方位俯仰电机的控制,从而调整视轴的指向;通过陀螺视轴反馈在惯性空间中的速度变化情况;通过码盘反馈反射镜相对于载机的角度变化情况;通过图像跟踪器反馈目标脱靶量,对视轴指向进行精确控制。其工作原理如图4所示。

图4 两轴稳定平台工作原理示意图Fig.4 Operating principle of dual-axis stabilization platform
单轴稳定回路的伺服控制系统流程如图5所示。

图5 单轴稳定回路结构框图Fig.5 Diagram of a single-axis stabilization loop
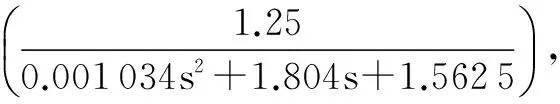
3.2 扰动分析与建模
当载机在惯性空间内运动时,会对光电稳定平台伺服系统产生惯性空间中的速度扰动。实验中通常采用角振动台产生的正弦扰动来模拟这种扰动。仿真中,将这种正弦扰动等效为 “总和扰动”加入到电压输入端,即加入如图6所示的幅值为1 V,频率为1.6 Hz的正弦电压扰动。
机载光电稳定平台的控制系统由于轴系间摩擦力矩、质量不平衡力矩、绕线力矩等扰动作用,往往存在单方向变化的干扰力矩,加入随时间线性变化的电压扰动w(k)=0.000 8×k+1来模拟这些力矩的 “总和扰动”,k随时间变化,每0.001 s增大1,即在仿真时间10 s内,扰动电压由1 V增大至9 V,如图7所示。

图6 正弦电压扰动Fig.6 Sine voltage disturbance
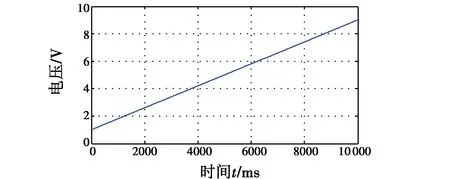
图7 线性电压扰动Fig.7 Linear voltage disturbance
3.3 仿真方法及结果
为研究基于BP神经网络的自抗扰控制器的性能特点,利用Matlab对基于BP神经网络的自抗扰控制器在机载光电稳定平台中的应用进行了仿真。
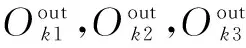
自抗扰控制器的非线性控制率有2个需要调整的参数k1,k2,本文也是用类似整定ESO参数的方式对这2个参数进行调整,其输入输出与前文所述的调整ESO参数的神经网络不同,输入分别为系统输入、系统输出、反馈误差和偏置值1,输出为k1,k2,输出系数也使用前文所述输出系数确定方法使用[25 000,250]。
为验证基于BP神经网络的自抗扰控制器的抗扰动效果,采用非线性自抗扰控制器作为对照,比较两者的性能差异。
得到的输出幅值对比如图8所示,图8a为自抗扰输出结果,图8b为BP神经网络自抗扰的输出结果。 图8a幅值约为6×10-4rad/s,图8b幅值约为2.4×10-4rad/s。可以看出,加入了BP神经网络的自抗扰控制器相对于传统自抗扰控制器的正弦扰动隔离效果提升了1.5倍。


图8 有正弦扰动的稳定精度曲线Fig.8 Stabilizing accuracy curves with sine disturbance
图9a为自抗扰输出结果,图9b为BP神经网络自抗扰的输出结果。
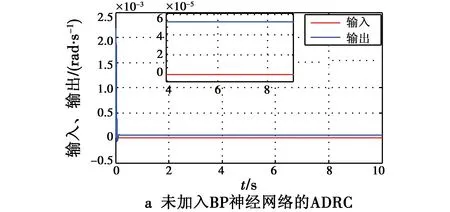
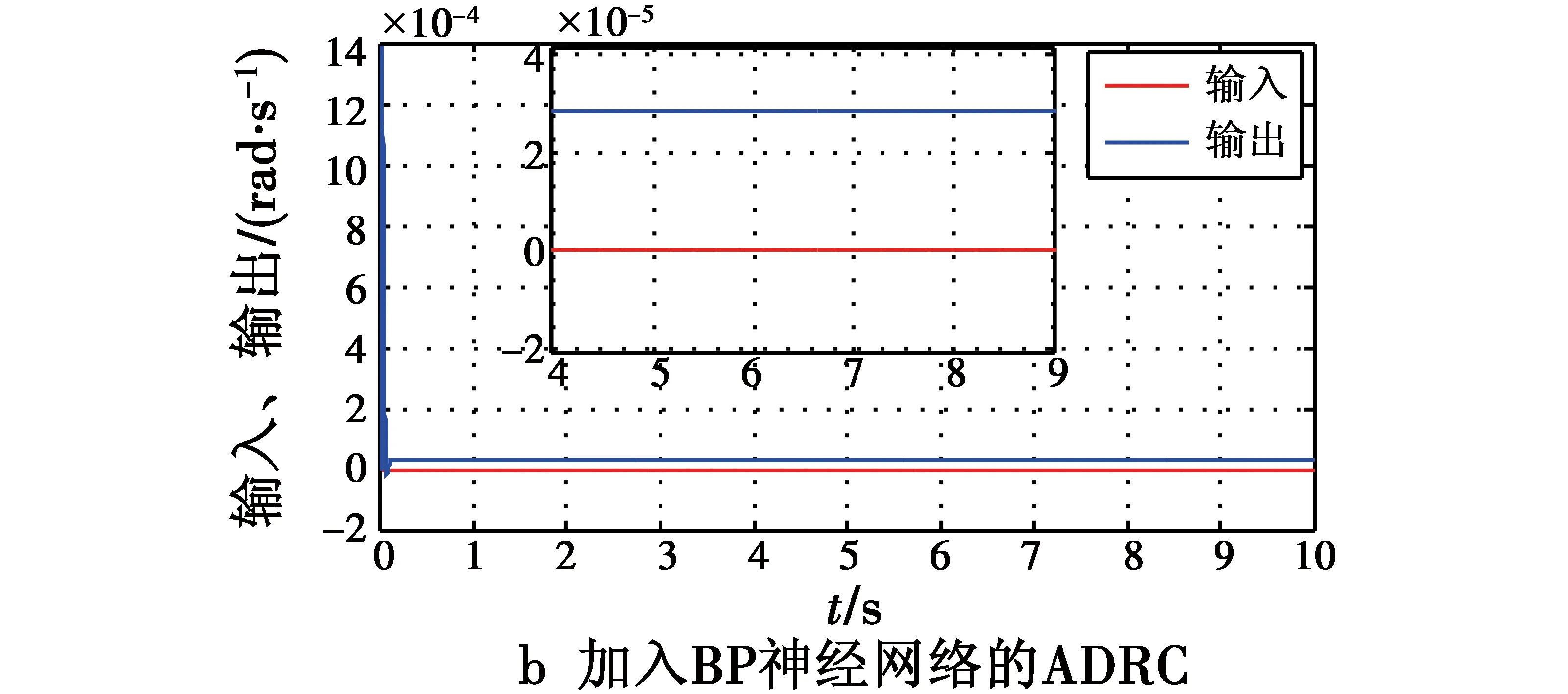
图9 加入线性变化扰动的稳定精度曲线Fig.9 Stabilizing accuracy curves with linear disturbance
图9a偏差峰值约为2.1×10-3rad/s,偏差稳态值约为5×10-5rad/s,图9b偏差峰值约为1.4×10-3rad/s,偏差稳态值约为3×10-5rad/s。可以看出,加入了BP神经网络的自抗扰控制器相对于传统自抗扰控制器的力矩扰动隔离效果提升了67%。
加入BP神经网络的自抗扰控制器性能比传统的自抗扰控制器更好,产生这样的仿真结果的原因主要有两点:1) BP神经网络迭代得到参数的方法快捷准确,有人工试凑参数无法比拟的优势;2) BP神经网络在迭代过程中会在线实时修改参数,使系统鲁棒性更强。
4 结语
本文以机载光电稳定平台的基于BP神经网络的自抗扰控制器为研究重点,对稳定回路及其扰动进行了分析和建模。对基于BP神经网络的自抗扰控制器调参方式进行了分析,提出了得出ESO参数迭代初值的方法,有效地提高了BP神经网络自抗扰控制器的收敛性,并与传统的自抗扰控制方法在机载光电稳定平台的应用进行分析、仿真,比较了这两种自抗扰控制器应用于机载光电稳定平台的性能优劣。仿真结果表明,基于BP神经网络的ADRC参数整定方法可以显著提高机载光电稳定平台自抗扰控制器的扰动隔离度,控制效果较传统的自抗扰控制方法有较大提升,对提高机载光电稳定平台的视轴稳定精度具有重要意义。
[1] 刘向.线加速度计在平台稳定系统中应用的理论研究[D].长春:中国科学院长春光学精密机械与物理研究所,2004.
[2] 张葆.《航空光电成像平台关键技术》专题文章导读[J].光学精密工程,2007,15(8):1280.
[3] 赵秀元,张新立,耿乐.扩张状态观测器的抑制扰动性分析[J].辽宁师范大学学报:自然科学版,2011,34(3):262-265.
[4] 郑颖.某集束火箭炮位置伺服系统自抗扰方法研究[D].南京:南京理工大学,2015.
[5] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2009.
[6] GAO Z Q.Scaling and bandwidth-parameterization based controller tuning[C]//American Control Conference, IEEE,2003:4989-4996.
[7] 齐晓慧,李杰,韩帅涛.基于BP神经网络的自适应自抗扰控制及仿真[J].兵工学报,2013,32(6)776-782.
[8] 段慧达.一类不确定高阶非线性系统的级联自抗扰控制策略研究[D].长春:吉林大学,2012.
[9] 李贤涛.航空光电稳定平台扰动抑制技术的研究[D].长春:中国科学院长春光学精密机械与物理研究所,2014.
[10] HILKERT J M,PAUTLER B.A reduced-order disturbance observer applied to inertially stabilized line-of-sight control[C]//Defense,Security,and Sensing,SPIE, 80520H (2011). doi: 10.1117/12.884123.
[11] 郑春艳,张红刚,冯兴伟,等.机载光电稳定平台自抗扰控制研究[J].电光与控制,2017,24(2):51-54.
[12] 邵立伟,廖晓钟,夏元清,等.三阶离散扩张状态观测器的稳定性分析及其综合[J].信息与控制,2008,37(2):135-139.

