量子粒子群优化的人工蜂群算法*

杜康宇, 毛 力, 毛 羽, 杨 弘, 肖 炜

(1.江南大学 物联网工程学院,江苏 无锡 214122;2.中国水产科学研究院 淡水渔业研究中心,江苏 无锡 214081)

0 引 言

人工蜂群(artificial bee colony，ABC)算法[1]具有结构简单、鲁棒性强、控制参数少、易于实现的优点，近年来受到越来越多国内外学者的关注，成为求解函数最优化问题的热点之一。但文献[2～6]表明与其他群智能算法一样，ABC算法在求解函数优化问题中具有收敛速度慢、局部搜索能力低的缺点。针对上述问题，葛宇等人[7]给出了一种新思路，针对跟随蜂的局部搜索行为提出了新方案，即基于极值优化策略高效率的寻优机制；文献[8]对传统ABC算法在自种群分组、种群架构、种群淘汰和步长更新方面进行了创新，引入了小生境技巧即时淘汰落入局部最优的蜜蜂个体，利用种群交叉的Z型分组方式，同时结合均匀设计理论建立初始种群；文献[9]利用逻辑运算创新地提出了离散人工蜂群算法，通过引入一系列的逻辑运算，不但成功避免了目前离散ABC算法中面临的解不更新问题，并且高效地保证了搜寻进程的中心解和最后解均封锁在原离散封闭集内，使算法的搜索效率大幅提高，成功地解决了实数集与离散集间的映射问题。以上方法在一定程度上使算法的精度提高了，改进了ABC算法在求解函数优化问题中的局部搜寻能力，对增强算法的性能和扩展其应用范围起到了重要的研究意义。

针对传统ABC算法中局部搜索能力较差，收敛速度慢等问题，本文提出了一种基于量子粒子群优化(quantum-behaved particle swarm optimization,QPSO)的人工蜂群算法,即QPSOABC算法。将QPSO算法中粒子位移的更新方法引入到了跟随蜂的搜索策略中，大幅提高了人工蜂群的局部搜索能力，同时算法的收敛速度和精度明显提高。

1 人工蜂群算法

人工蜂群算法是一种新的随机搜索方法，模拟了蜂蜜的行为模式，并成功地应用于函数优化问题[10～12]。算法的具体描述如下：

1)初始化：在规定的上下界中随机生成SN个可行解(蜜源)Xi=(Xi1，Xi2，…，XiD)，每个解与蜜源、雇佣蜂和跟随蜂一一对应。

2)雇佣蜂搜索阶段：随机选择蜜源中的任意一维分量按式(1)进行变异，搜索新蜜源

vi,j=xi,j+rand(-1,1)(xi,j-xk,j)

(1)

式中Vi,j为新蜜源的位置；xi,j为个体Xi的第j维分量；xk,j为个体Xk的第j维分量。进入采蜜过程，雇佣蜂通过贪婪选择策略对新蜜源进行筛选，选取适应度较高的蜜源。

3)跟随蜂搜索阶段：搜索过程完成后，雇佣蜂将传递蜜源信息给跟随蜂，根据式(2)、式(3)计算出选择跟随蜂的概率，并通过轮盘赌的形式对适应度值较高的优质蜜源进行更新，其中，跟随蜂的更新公式和式(1)相同

(2)

(3)

式中fi为目标函数f(Xi)的适应度值；fiti为蜜源Xi对应的适应度。

4)侦查蜂搜索阶段：如果蜜源在连续循环的规定时间后没有改善，即转化为侦察蜂。侦察蜂根据式(4)随机生成一个新解取代当前解，并记录新蜜源适应度

Xi=Xmin+rand(0,1)(Xmax-Xmin)

(4)

式中Xmax和Xmin为解空间的上、下边界。

2 改进人工蜂群算法

在算法的寻优过程中，雇佣蜂负责全局搜索，侦察蜂由进化停滞的雇佣蜂转化而来，处理进化停滞的个体，也属于全局搜索，该算法全局搜索能力较强；原始ABC算法中，跟随蜂的更新公式和雇佣蜂的跟随公式相同，即算法局部搜索能力较差，因此，将其他算法中的局部更新方式与跟随蜂的局部更新方式进行结合即可相应提高算法的精度和收敛速度。

2.1 基于QPSO的跟随蜂局部搜索策略

在传统的ABC算法中，雇佣蜂与跟随蜂的搜索策略完全相同，因此,跟随蜂的全局搜寻能力非常强大，但局部搜寻能力相对较弱。在改进的算法中，为了提高跟随蜂的局部搜寻能力，利用雇佣蜂个体极值和全局极值进行局部寻优，且在每次迭代中逐维更新蜜源每一维度的值，以确定蜜源是否改进。

该算法融合量子能够遍历整个解空间的行为特性，根据蜜源位置的波函数与概率密度函数，基于量子δ势阱模型进行位移更新，QPSO中的位移操作实质上是一种局部搜索策略，跟随蜂按照式(5)～式(7)更新位置

P=aPbest+(1-a)Gbest

(5)

b=1.0-g/maxg×0.5

(6)

(7)

式中a,u为(0，1)之间的随机数；Pbest为个体极值；Gbest为全局极值；b为收缩膨胀系数；g为当前进化代数；maxg为规定的最大进化代数。

传统的ABC算法每次都只修改一个维度的值，这样做改变的内容较少。

2.2 QPSOABC算法流程

对于最小值优化问题Minf(X)，改进ABC算法实现的具体步骤如下：

1)初始化算法参数，随机产生SN个解，每个解Xi=(Xi1，Xi2，…，XiD)为一个D维向量，最大迭代次数MCN，并指定控制参数limit的值，用于确定个体是否更新停滞。

2)对种群中每个雇佣蜂Xi在D维空间中利用式(1)逐维搜索，若新个体较原个体优秀则更新；否则，保留Xi。

3)记录雇佣蜂变化之后的个体极值Pbest和全体极值Gbest，并将其代入式(5)得到的结果代入式(2)和式(3)，并计算每个食物源被选择的概率。

4)跟随蜂遵循轮盘赌的方式在部分优质蜜源附近局部搜索，选择部分适应度值较高的蜜源，然后每个跟随蜂在D维空间内利用式(7)更新种群中的所有蜜源。

5)当蜜源在连续limit次迭代后未更新时，根据式(4)随机生成一个新蜜源替代原蜜源。

6)记录当前的最优解。

7)判别是否达到最大迭代次数MCN，如果满足，则输出最优解；否则，转到步骤(2)。

3 仿真实验分析

为评估QPSO算法的性能，本文采用6个典型的测试函数[13]对QPSOABC算法、ABC算法以及文献[14,15]中改进ABC算法的稳定性、收敛速度和寻优精度进行对比实验。

3.1 测试函数选择

表1列出了6个测试函数的搜索范围和理论最优值。其中：f1～f3为单模态函数，在定义域内只有一个极值点，主要用于测试函数的收敛速度和寻优精度；f4～f6为非线性多模态函数，存在多个局部极值点，用于测试算法的全局寻优性能和避免早熟的能力。

表1 测试函数的搜索范围和理论最优值

6种函数形式如下：

Penalized2函数

3.2 实验结果与分析

在QPSOABC，Best-so-far ABC，ABC 3种对比算法的实验中，参数设置如下：种群规模SN=50，确定是否落入停顿的循环控制参数limit=10，维度D=30，最大迭代次数MCN=1 000。

为了测试该算法的性能，采用上述3种算法对6个测试函数在30维的条件下进行30次独立实验，记录其所对应的最优值、最差值、平均值、标准差和平均耗时，平均耗时即6个测试函数在单独运行30次到达收敛稳定精度所需要的时间的平均值。

表2中的数据表明：传统的ABC算法具有收敛速度慢、收敛精度不高、算法稳定性较差的缺点；Best-so-far ABC算法采用当前最优解及其对应的适应度值改良跟随蜂的邻域搜寻方式，从而提高了算法的局部搜寻能力，使算法的质量有了较大提高。QPSOABC算法将量子粒子群优化算法中粒子位移的更新方法引入到了跟随蜂的局部搜索策略中，大幅提高了人工蜂群的局部搜索能力，使该算法的收敛速度和精度明显提高。

在测试函数f1,f2中，由于Best-so-far ABC算法陷入局部最优解，因此出现了方差较小的结果。针对单峰函数sphere函数f1、多峰Schwefel函数f2、The Rotated Elliptic函数f4以及Griewank函数f5，由于传统ABC的随机性问题，收敛速度明显较其他2种算法慢，而Best-so-far ABC算法中虽然最终效果相对原算法较好，但是前期收敛速度慢，并且后期由于部分个体落入局部最优解的问题，使得算法精度并未达到理想的效果。本文算法可以有效地避免局部优化，收敛速度快，可以收敛到理想的精度。针对单峰Rosenbrock函数f3，多峰Penalized2函数f6，传统ABC算法和Best-so-far ABC算法的收敛速度和收敛精度均很不理想，本文改进的算法收敛速度和收敛精度明显改进，不过未克服易陷入局部最优的问题，算法仍有改进空间。

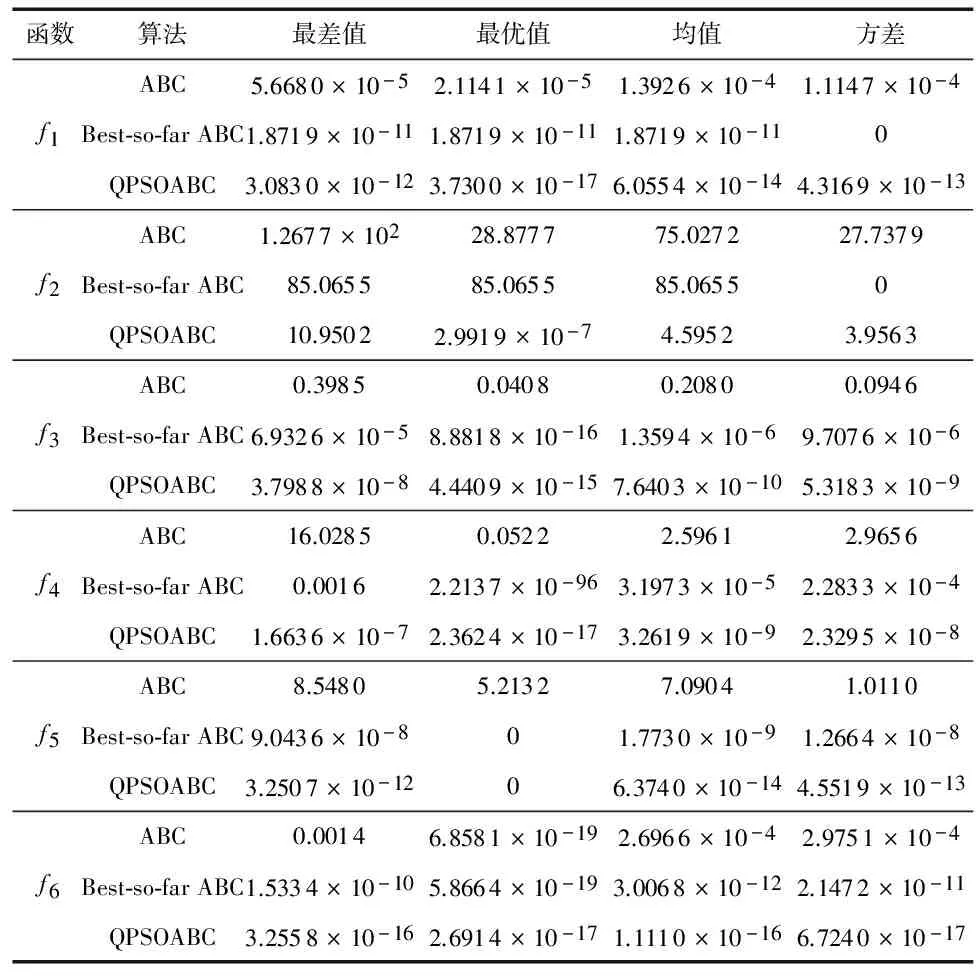
表2 30维函数测试结果

上述实验结果表明：与传统ABC算法和Best-so-far ABC算法相比，QPSOABC算法具有更快的收敛速度和更高的收敛精度。QPSOABC算法将量子粒子群优化算法中粒子位移的更新方法引入到跟随蜂的局部搜索策略中，大幅提高了人工蜂群的局部搜索能力，使算法的收敛速度和精度明显提高。

4 结束语

根据传统ABC算法的不足，提出了一种针对跟随蜂局部搜索能力的具体改进方案。算法将量子粒子群优化算法中粒子位移的更新方法引入到跟随蜂的局部搜索策略中，大幅提高了人工蜂群的局部搜索能力，使该算法的收敛速度和精度明显提高。仿真实验结果表明：在求解函数最小值优化问题时，本文算法不仅可以有效避免函数陷入局部最优，而且具有较好的鲁棒性，进而提高了算法的收敛速度和寻优精度。

[1] Karaboga D,Basturk B.On the performance of artificial bee colony(ABC)algorithm[J].Applied Soft Computing,2008,8(1):687-697.

[2] Sarangi P P,Sahu A,Panda M.Training a feed-forward neural network using artificial bee colony with back-propagation algorithm[J].Advances in Intelligent Systems & Computing,2014,243:511-519.

[3] Karaboga D,Ozturk C.Neural networks training by artificial bee colony algorithm on pattern classification[J].Neural Network World,Neural Network World,2009,19(3):279-292.

[4] Banharnsakun A,Sirinaovakul B,Achalakul T.Job shop scheduling with the best-so-far ABC[J].Engineering Applications of Artificial Intelligence,2012,25(3):583-593.

[5] 孙凌宇,冷 明,朱 平.一种基于贪心策略的启发式云计算任务调度算法[J].井冈山大学学报:自然科学版,2015(6):56-61.

[6] 丁婷婷,高美凤.改进粒子滤波的无线传感器网络目标跟踪算法[J].传感器与微系统,2016,35(7):140-142.

[7] 葛 宇,梁 静,王学平,等.求解函数优化问题的改进的人工蜂群算法[J].计算机科学,2013,40(8):252-257.

[8] 臧明相,马 轩,段奕明.一种改进的人工蜂群算法[J].西安电子科技大学学报:自然科学版,2015,42(2):65-70.

[9] 邱剑锋.人工蜂群算法的改进方法与收敛性理论的研究[D].合肥：安徽大学,2014.

[10] Banharnsakun A,Achalakul T,Sirinaovakul B.The best-so-far selection in artificial bee colony algorithm[J].Applied Soft Computing,2011,11(2):2888-2901.

[11] Li X,Yang G.Artificial bee colony algorithm with memory[J].Applied Soft Computing,2016,41:362-372.

[12] Li X,Yin M.Parameter estimation for chaotic systems by hybrid differential evolution algorithm and artificial bee colony algo-rithm[J].Nonlinear Dynamics,2014,77(1-2):1-11.

[13] 张银雪,田学民,曹玉苹.改进搜索策略的人工蜂群算法[J].计算机应用,2012,32(12):3326-3330.

[14] Banharnsakun A,Achalakul T,Sirinaovakul B.The best-so-far selection in artificial bee colony algorithm[J].Applied Soft Computing,2011,11(2):2888-2901.

[15] 罗 浩,刘 宇.一种强化互学习的人工蜂群算法[J].计算机工程与应用,2016,52(16):23-29.