融合密度峰值和模糊C-均值聚类算法*

任新维， 张桂珠

(江南大学 物联网工程学院 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

0 引 言

各类聚类分析的算法中，模糊聚类可以描述样本类的中介性，从而更客观地反映真实的世界，成为非监督模式识别的一个重要分支，其中模糊C—均值(fuzzy C-means,FCM)聚类算法是运用最广泛的模糊聚类算法[1～3],但算法也存在着很多不足，如：对初始值过于敏感，容易陷入局部最优，整体效率不高等[4,5]。密度峰值聚类[3](density peaks clustering,DPC)算法是Alex Rodriguez和Alessandro Laio提出的一种新的基于密度的聚类算法，其基本思想简单且效率高，对于任意形状的数据集，能够快速发现其密度峰值点，但算法聚类效果在某种意义上依赖于用于计算局部密度的截断距离dc，而文献[6]并没有给出dc的计算方法；其次，对同一个类存在多密度峰值的情况，该算法聚类效果并不理想。

针对FCM算法和DPC算法存在的上述缺点，本文提出了DPC-FCM算法。实验结果表明DPC-FCM算法具有更好的聚类效果。

1 DPC算法及其改进

1.1 算法基本思想[6]

理想的类簇中心周围有局部密度较低的相邻点围绕，且与更高密度的任何点有相对较大的距离。为了准确找到上述条件的类簇中心，需要计算每个数据点i的两个量：局部密度ρi和数据点i到更高局部密度点j的最短距离δi，以刻画聚类中心。ρi有Cut-off kernel和Gaussian kernel两种计算方式，Cut-off kernel为

(1)

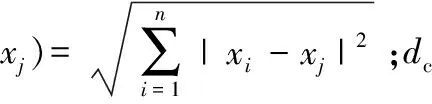
(2)

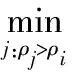
(3)

分别计算出样本数据集中所有数据点xi的ρi，δi。然后再计算一个将ρ值和δ值综合考虑的量γ

γi=ρiδi,i∈Is

(4)

将余下的数据点分配到与其距离最近且密度较其更高的点所属的簇。然后算法定义每个簇的边界区域密度ρb：属于某个簇并且与属于其他簇的数据点之间的距离小于截断距离dc的数据点总数。密度较ρb高的点视为核心点，其余的点视为噪声点，由此得到聚类的最终结果。

1.2 算法的局限性[6]分析

1)关于数据集规模的大小判断没有确切的衡量标准，导致样本密度计算方式的选取可能影响聚类的结果。

2)如果有一个样本数据的聚类中心归类出现了错误，即导致最终的聚类结果千差万别。

3)对于比较复杂的数据集，由于不同类簇之间密度可能会有较大的差异，此时DPC算法如果继续在欧氏距离测度下进行聚类[7,8]，取值不同的截断距离dc就会产生不同的聚类结果，很容易得到错误结果。

1.3 DPC算法的改进

本文采用了一种新的自适应度距离来对DPC算法进行改进。在现有多种相似度度量中，自调节相似度[9]计算方法考虑到了邻域数据分布对两点相似度的影响，准确反映复杂结构数据集的分布特点

(5)

式中σi=d(si,sk)，其中点sk为si的第K个近邻点;σi为点si与sk的欧氏距离，根据文献[9]令K=7，可以在高维数据的条件下得到较好的结果。在自适应相似度测度下查看Jain数据集，设点a处在高密度簇中而点c处在低密度簇中，显然σa<σc，可以推出σaσb<σcσb，从而得到Aab>Abc，由此可以看出,采用自适应相似度的计算方法可以更好地度量不同密度簇之间点的相似度。本文将自适应相似度转换为权值加入到欧氏距离公式中，生成了一种新的加权欧氏距离公式

(6)

式中Aij∈[0,1]为点i和点j的自适应相似度。

权值wi=1-Aij

(7)

在采用具有加权欧氏距离公式计算相似度后，各个对象之间的差异可以更准确地算出来，DPC算法可以基于此公式计算每个数据点的局部密度ρi和点i到局部密度更高点的最近距离 ，从而更准确地选取聚类中心点，提高聚类结果的准确率。

2 FCM聚类算法

FCM聚类算法描述为：

1)确定类的个数k，指数权重α，初始化隶属度矩阵U(0)。令m=1表示第一步迭代。

2)计算聚类中心。给定C(m)，计算U(m)。

3)重新计算隶属度。给定U(m)，计算C(m)。

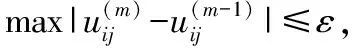
经过上述4步的多次迭代，可以得到最终的隶属度矩阵U和聚类中心V，使得目标函数J(U,V)最小，再根据隶属度矩阵U划分样本的最终分类。

3 DPC和FCM的融合算法

3.1 算法思想

算法分为2个阶段：1)对每个数据计算两个量ρi和δi,刻画聚类中心，ρiδi值越大，该点越可能是聚类中心；2)运用标准的FCM算法进行迭代，获得更好的聚类结果。

3.2 算法步骤

DPC-FCM算法总体如下：

阶段一:执行DPC算法，确定初始聚类中心。

输入:样本数据集X

输出:聚类中心ci(k)。

1)根据加权欧氏距离公式计算数据点之间的距离；

2)根据步骤(1)计算的m=n(n-1)/2个距离进行升序排列，设得到的序列为d1≤d2≤…≤dM,取该序列前2 %的数据，确定截断距离dc;

3)在步骤(1)得出的距离基础上，计算每个数据点的局部密度ρi和数据点到局部密度较其大且距其最近的点的距离δi；

4)计算γi=ρiδi，绘制决策图，γ越大越有可能是聚类中心，由此得到ci(k)。

阶段二:执行FCM算法。

输入:迭代终止条件ε、模糊指数α、样本数据集X、聚类中心ci(k);

输出:隶属度矩阵U、聚类中心C。

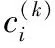
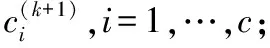
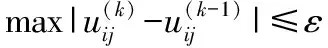
5)在完成上述4步的多次迭代后，根据最终得到的隶属度矩阵U划分样本的最终分类。

4 实验分析

为了证明DPC-FCM算法的有效性，采用Iris数据集和Wine数据集以及一组人工数据集Dataset对2种算法进行仿真实验。使用MATLAB R213a进行实验，表1为用于实验的各个数据集构成。

表1 实验数据集的构成描述

选取UCI中的Iris数据集进行验证，此数据集包含150个样本，来自于三类莺尾花的花朵样本，每一类包含50个样本，每个样本又包含4个属性：sepal length，sepal width，petal width，petal length，利用改进的DPC算法选取聚类初始中心，然后与Iris实际的数据集进行对比，如表2所示。

可以看出，本文提出的改进算法选取的聚类初始中心与Iris数据集实际的中心非常接近，验证了本文算法有效性。

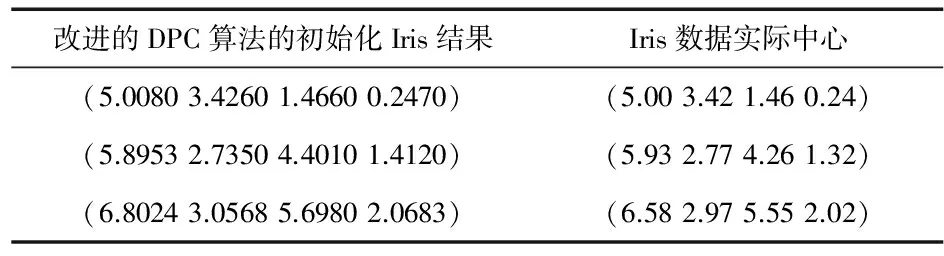
表2 初始聚类中心选取对比

在MATLAB仿真实验中，对原始的FCM算法、DPC-FCM算法在Dataset，Wine，Iris数据集逐个进行50次试验，计算聚类正确数的平均值，得到的实验结果如表3所示。

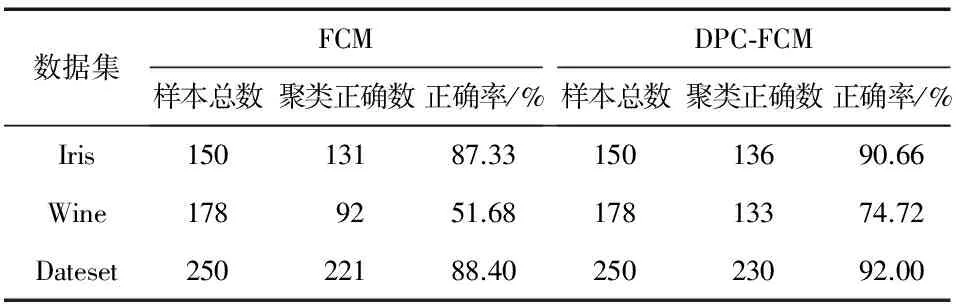
表3 聚类正确结果对比

可以看出，FCM算法对初始值比较敏感，聚类效果比较差，尤其是在Wine这种相对复杂的数据集上，随机选取聚类中心导致最终聚类结果不理想；而DPC-FCM算法将DPC与FCM结合，利用了DPC算法的选取聚类中心较为准确的优势，与传统的FCM算法相比，聚类效果得到了提升。

图1为对Iris，Wine和自定义数据集Dataset分别应用FCM，DPC-FCM算法的收敛速度对比。由图可知，FCM寻优能力较差，过分依赖于初始的聚类中心。而DPC-FCM算法，能更准确地得到聚类中心，收敛速度更快，在寻优效果和全局搜索能力上均有较好的表现。

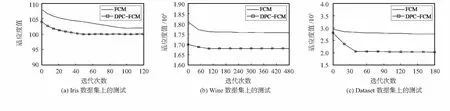
图1 在不同数据集上的测试

采用F-measure指标、Rand指数和Jaccard系数对聚类结果进行评估。

F-measure计算公式如下

(8)

式中P为精确率；R为召回率。F-measure指标取值范围为[0,1]，值越大表明聚类效果越好。

此外，Rand指数可以反映出聚类结果与最初数据集之间的分布；而Jaccard系数越大代表聚类效果越好。

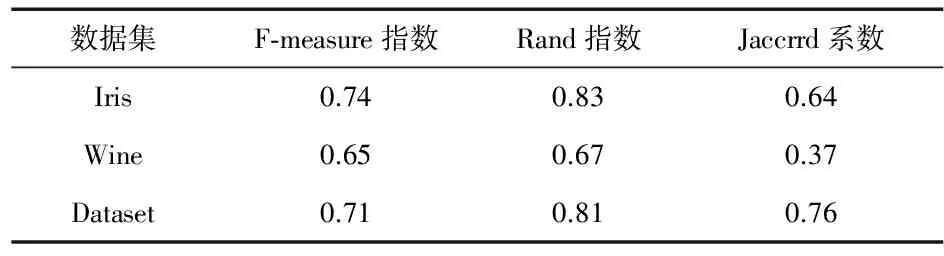
表4 FCM算法实验结果

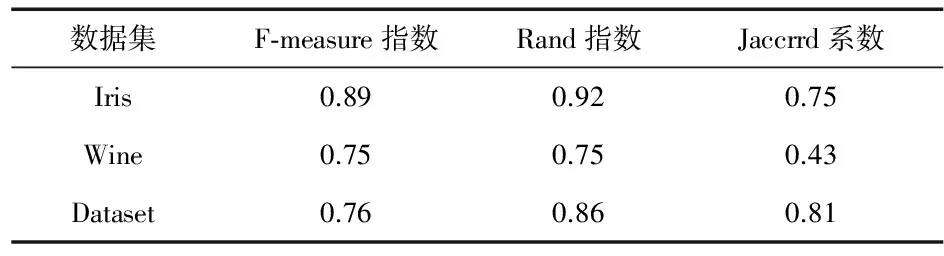
表5 DPC-FCM算法实验结果

从表4和表5可以看出，DPC-FCM算法的聚类结果优于FCM算法。

5 结 论

通过实验数据的分析可知，DPC-FCM算法提高了聚类正确率、全局收敛速度和优化精度，有效地提高了聚类的稳定性和准确性。

[1] 付争方,朱 虹.基于模糊理论的低照度彩色图像增强算法[J].传感器与微系统,2014,33(5)：121-124.

[2] 张国锁,周创明,雷英杰.改进FCM聚类算法及其在入侵检测中的应用[J].计算机应用,2009,29(5):1336-1338.

[3] Rodriguez Alex,Alessandro Laio.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[4] Zelnik-Manor L,Perona P.Self-tuning spectral clustering[J].Advances in Neural Information Processing Systems,2004,17:1601-1608.

[5] 李文杰，廖晓纬，束仁义，等.基于ZigBee和模糊C均值聚类算法在火警中的应用[J].传感器与微系统，2012,31(10):143-152.

[6] 杨 燕，靳 蕃，Kamel M. 聚类有效性评价综述[J].计算机应用研究,2008,41(6):1631-1632.

[7] 韩晓慧，王联国.一种基于改进混合蛙跳的聚类算法[J].传感器与微系统，2012,31(4):137-139.

[8] 高孝伟.权熵法在教学评优中的应用研究[J].中国地质教育,2008,17(4):100-104.

[9] 华 漫,李燕玲,魏永超.基于自适应相似度距离的改进FCM图像分割[J].电视技术,2016,40(2):33-36.