非饱和区扩展的RNN算法优化*

张 尧， 沈海斌

(浙江大学 超大规模集成电路设计研究所，浙江 杭州 310027)

0 引 言

循环神经网络(recurrent neural network,RNN)是目前最流行的人工神经网络之一，具有处理历史信息和建模历史记忆的功能特点，适用于处理时间、空间上有关联的信息，如语音识别、实时翻译以及计算机视觉等[1～3]。在标准的RNN结构中，随着序列数据的不断输入，覆盖之前的序列数据信息，导致序列梯度消散问题[4], Karpathy A等人采用了长短时记忆(long short-term memory，LSTM)单元解决该问题[5]。LSTM型RNN使得激活函数的数量增加，激活函数一般为S型函数，如Sigmoid, Tanh等[6]。LSTM型RNN隐含层一般采用2层结构，单层网络训练效果不佳，多层网络训练难度较大。采用反向传播算法进行训练时，S型函数容易进入导数趋近于0的饱和区导致收敛速度慢。Glorot X等人采用了修正线性单元(rectified linear units,ReLU)训练具有稀疏特性的数据，解决S型激活函数饱和区难以收敛的问题[7]。ReLU是分段线性非饱和函数，随着x的增大，函数发散，训练时容易导致梯度爆炸，无法完成训练。

本文提出了扩展激活函数非饱和区的方法解决了S型激活函数饱和区收敛速度慢和ReLU激活函数梯度爆炸的问题，加快了LSTM型RNN的训练收敛速度。

1 LSTM型RNN训练

1.1 LSTM型RNN的前向传播

前向传播过程从t=1时刻依次经过输入层、隐含层和输出层。

Input Gate

(1)

(2)

Forget Gate

(3)

(4)

Cell

(5)

(6)

式中wic,whc分别为输入层、隐含层与Cell单元的连接权值。

Output Gate

(7)

(8)

Cell Output

(9)

1.2 LSTM型RNN的后向传播

Cell Output

(10)

式中G为隐含层输入的个数，包括LSTM单元之间的连接和不同门之间的连接。

Output Gate

(11)

State

(12)

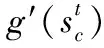
Cell

(13)

Forget Gate

(14)

Input Gate

(15)

2 非饱和区扩展的RNN算法优化

LSTM单元中的Input Gate,Output Gate和Forget Gate一般采用Sigmoid函数作为激活函数，Net Input单元和Cell单元一般采用tanh函数作为激活函数[8,9]。Sigmoid函数和tanh函数具有类似的函数特征，即非线性、饱和性

(16)

(17)

不同系数的Sigmoid和tanh函数及其导数图像如图1、图2所示。Sigmoid函数和tanh函数的系数不同时，函数的非线性、饱和性不同。系数变大时，非饱和区变窄，非饱和区的导数变大；系数变小时，非饱和区变宽导数变小。

图1 k-Sigmoid函数及其导数

图2 k-tanh函数及其导数

3 实验结果与分析

不同系数激活函数的LSTM型RNN训练过程中训练时间和训练误差如图3所示，k为激活函数的系数。实验结果表明:当激活函数系数为1/8时，训练速度最快。激活函数系数较大时，非饱和区较窄；系数过小时，非饱和区导数较小，因此,选择激活函数系数为1/8。同等误差水平下，RNN的训练时间减少了21 %(k=1的训练时间为26 129 s，k=0.125的训练时间为20 520 s)。

图3 参数化激活函数的RNN训练过程

4 结束语

基于S型激活函数的性质，提出了参数化激活函数方法，有效地扩展了激活函数非饱和区范围，通过实验证明了非饱和区扩展的RNN算法优化方法加快了训练的收敛速度。实验中，不同的初始化权值以及神经元结点数，对训练的误差和速度影响不同，如何选择最优的LSTM型RNN的参数是今后的研究方向。

[1] Zen H.Acoustic modeling in statistical parametric speech synthesis-from HMM to LSTM-RNN[J].Middle East Policy,2008,15(1):125-132.

[2] Kim J,Kim J,Thu H L T,et al.Long short term memory recurrent neural network classifier for intrusion detection[C]∥2016 International Conference on Platform Technology and Service(PlatCon),IEEE,2016:1-5.

[3] 李幸超.基于循环神经网络的轨迹位置预测技术研究[D].杭州：浙江大学,2016.

[4] Graves A.Neural networks[M].Berlin Heidelberg:Springer， 2012:15-35.

[5] Karpathy A,Johnson Justin,Li F F.Visualizing and understan-ding recurrent networks[C]∥International Conference on Learning Representations(ICLR),San Juan:2016.

[6] 李宏伟,吴庆祥.智能传感器中神经网络激活函数的实现方案[J].传感器与微系统,2014,33(1):46-48.

[7] Glorot X,Bordes A,Bengio Y.Deep sparse rectifier neural networks[J].Journal of Machine Learning Research,2014,33(1):46-48.

[8] Krizhevsky A,Sutskever I,Hinton G E.ImageNet classification with deep convolutional neural networks[J].Advances in Neural Information Processing Systems,2012,25(2):2012.

[9] Soleymani M,Asghari Esfeden S,Fu Y,et al.Analysis of EEG signals and facial expressions for continuous emotion detec-tion[J].IEEE Transactions on Affective Computing,2016,7(1):1.