晶面偏角对利用Voigt函数法计算硅单晶本征晶格应变的影响∗

朱杰 姬梦 马爽

(同济大学物理科学与工程学院,精密光学工程与技术研究所,先进微结构材料教育部重点实验室,上海 200092)

1 引 言

随着科技的日益发展,Si作为半导体工业最主要的材料已经广泛应用于我们生活中各个方面,从太阳能、计算机芯片到手机通信处处可见Si的身影.由于Si单晶材料优异的半导体特性、稳定的性能以及低廉的价格在我们的日常生活以及科研领域扮演着不可或缺的角色,如集成电路基片、偏振镜、X射线单色器、聚焦镜等.Zaprazny等[1]应用具有大晶面偏角的硅锗单晶进行了X射线成像研究;Guigay和Ferrero[2]发现具有晶面偏角的硅弯晶比平晶有着更好的聚焦效果;杨德仁等[3]应用单晶体X射线衍射半高全宽研究了Si晶片切割造成的损伤层微观应力;赵炳辉和陈立登[4]应用双晶衍射曲线半高全宽研究了硅片的机械强度;朱南昌等[5]应用衍射曲线研究了晶体表面畸变.由于Si应用广泛,研究Si单晶材料的物理特性显得非常重要.通常情况下,晶体研究最常用的方式是X射线衍射,通过衍射曲线的半高全宽、积分宽度、峰值位置或者衍射强度等物理参数可以获得晶体晶向、质量、应力、缺陷、衍射效率等重要信息.除了表面加工质量、粗糙度、晶向、内部缺陷等因素之外,晶面偏角也是影响衍射曲线线形及宽度的重要因素之一.很多有关Si单晶的研究都需要考虑偏角的影响[6].单晶Si在从定向、切割、加工到成品过程中,其实际表面与晶体内部晶面之间必然会存在一定夹角,称之为晶面偏角(asymmetry angle).用作基片的Si单晶其晶面偏角通常在0.5°左右,一些其他样品达到了1°甚至更高的偏差.通常的研究均将晶体样品当作近完美单晶或镶嵌块(mosaic)结构,很少考虑晶面偏角对晶体物理性能的影响.而当晶体存在一定偏角时入射光线和衍射光线与实际样品表面的夹角不再对称相等,晶体的X射线衍射曲线将发生变化,特别是衍射曲线半峰宽和积分宽度这两项物理参数有较大改变,如果忽略晶面偏角将会使晶体X射线测量分析误差增加.本文以Si(111)晶面的晶格微观应变ε为例来分析晶面偏角在Si单晶X射线衍射测量中的影响.

由于晶体在生长、加工制造过程中,要经过高温生长、提拉、搬运、切割、研磨抛光、退火等诸多工序,在外力作用下其内部不可避免地存在残余应力应变,通过对晶体应力应变的测量可以很好地了解其内部物理特性和质量好坏.如Huang等[7]研究了Si单晶的动力学形变,孙云等[8]应用高分辨X射线衍射技术研究了KDP晶体的晶格应变,从而可以在加工KDP晶体时注意容易开裂的Z轴[001]方向.应力应变的研究对晶体的制备加工与应用有十分重要的意义和研究价值.单晶材料的应力应变测量方法有很多,一般采用双晶X射线衍射的Bond法,或者需要知道理论上无应力时理想晶体的晶面间距d值进行计算[9−11],d值的精确测定影响着应力应变的准确性,日本学者Suzuki等[12]提出了线性回归方法较好地改进了d值不可靠所带来的影响.其中最为简便的是Langford[13]提出的Voigt函数法,该方法认为晶体内部微观应变引起的宽化可以用Gauss函数近似,晶粒尺寸所引起的线形宽化可以用Cauchy函数来近似,通过对衍射曲线进行Voigt函数拟合,得到半高全宽ω、积分宽度β以及形状因子φ,计算出Gauss成分的积分宽度βG,代入相关公式即可求出微观应变ε.因此利用X射线衍射(XRD)技术测定晶体的应力应变时半高全宽值以及积分宽度成为非常重要的物理参数,这些物理参数又同晶面偏角密切相关.这里着重针对Voigt函数法分析晶体微观应变时不同晶面偏角对测量值的影响来进行分析.

2 基本原理

2.1 晶格应变的计算原理

晶体内应力按性质可分为三大类[14]:在宏观范围内的第一类应力使晶面间距发生改变导致X射线衍射谱线的位移;而在晶粒范围内的第二类内应力则使晶面发生弯曲变形导致谱线展宽;在单位晶胞内的第三类内应力是由点缺陷、线缺陷和面缺陷使衍射强度下降,因此通过X射线晶体衍射的方法可以研究晶体内应力以及应变.研究不同类型的内应力时应该消除其他因素的影响,以免实测衍射曲线为多种因素的叠加从而增加分析难度.晶格的应变伴随着晶面间距d值的变化,根据弹性力学理论这种变化是由内应力产生的弹性应变,测量这种应变最直接的方法是利用X射线衍射.入射X射线以一固定波长入射到晶体时,当入射角度满足布拉格条件,X射线将会在晶格点阵组成的规则晶面上发生衍射增强的现象,可以用公式2dsinθB=nλ表示(d为晶面间距,θB为布拉格角,λ为入射X射线波长,n为衍射级次).当内应力的存在改变了晶面间距d值时,其变化量为Δd,布拉格角也会产生微小的偏移ΔθB(布拉格偏离角),修正后的布拉格方程可以表示为

通常情况下,只考虑一级衍射,n=1,在衍射分析中可以简化成,进行微分可以得到

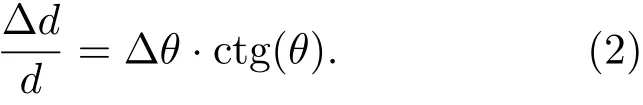
晶格点阵的应变ε即可以写成ε=Δd/d=ΔθBctg(θB),当布拉格角有偏移时其衍射曲线也必将发生变化(包括的峰型、半高全宽和积分宽度).

2.2 衍射曲线峰型与应变的关系

影响晶体实测X射线衍射曲线峰型的因素有很多,测量得到的衍射曲线主要是由本征结构峰和展宽卷积而成[15].晶体衍射的本征衍射峰型接近Gauss分布,而其他各种因素导致的线形展宽接近Cauchy分布,如果测量峰型为h,本征结构峰为g,展宽为f,那么衍射曲线的峰可以用下面公式描述:

其中下标C和G分别代表Cauchy分量和Gauss分量,二者在不同比例下卷积得到Voigt峰型函数(即本文实测峰型).我们可以通过下面的表达式获得Cauchy分量和Gauss分量的曲线积分宽度,分别为βC和βG,2ω和β分别为衍射曲线的半高全宽和积分宽度:

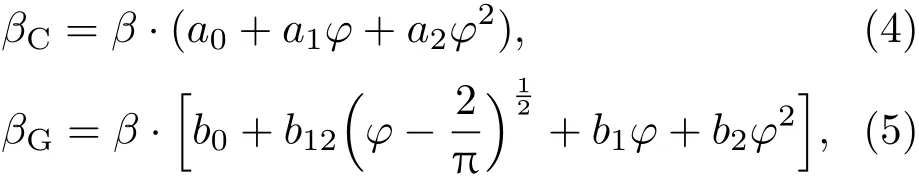
式中φ =2ω/β为形状因子,a0=2.0207,a1=−0.4803,a2=−1.7756,b0=0.6420,b12=1.4187,b1=−2.2043,b2=1.8706.

Langford的研究[13]表明,对单一的衍射曲线而言,可以认为晶粒尺寸大小提供了Cauchy分布的线形,而Gauss分布来源于晶体内部的应变ε.那么对晶体而言内部晶粒尺寸大小D和应变ε就可以用下面的公式表示:

(7)式给出了应变与Gauss分量积分宽度之间的关系,如果测量实际晶体的衍射曲线,根据峰型求得半高全宽2ω和积分宽度β,再通过(5)式就可以计算出内部微观应力积分宽度βC和βG,然后根据(6)和(7)式求出晶粒尺寸和微观应变ε.需要注意的是,由于Voigt函数法对其中的系数k非常敏感[16],在不同线形组合时所求得的晶粒尺寸相差甚大,必须经过修正才能得到较为准确的数值,而微观应变对此不是很敏感,特别是当衍射曲线基本接近Gauss分布时计算结果和理论值相差不大,可以接受[17].因此实验所用Si单晶均研磨抛光至近完美晶体水平,排除晶粒细化所带来的峰型展宽,从而使结果更加准确.

2.3 带有晶面偏角的晶体衍射曲线半高全宽理论计算

根据Darwin所给出的完整理想晶体在全反射范围内单晶反射曲线的半高全宽(以弧度表示)ω的计算公式[18]:

式中N为单位体积(1cm3)内的晶胞数1/Ω,Ω为晶胞体积;Fg为反射晶面的结构振幅(也称结构因子);C为偏振因子

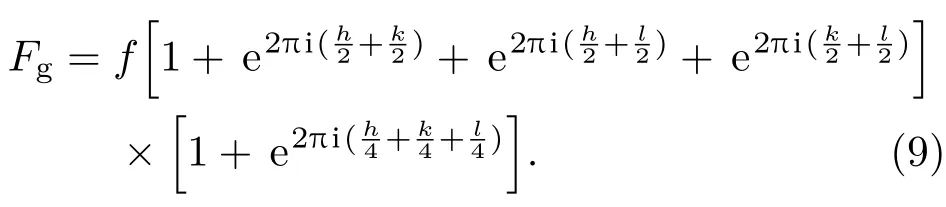
本文以Si(111)为例,将晶面指数(111)代入(9)式可得结构因子为

代入(8)式即可得出理想Si单晶(111)晶面的衍射峰半高全宽为

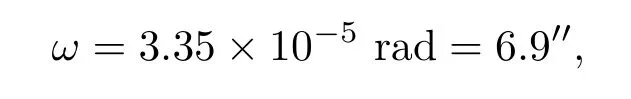
这是理想情况下所得到的半高全宽值,实测中由于晶体本身的不完美,内部缺陷以及光源和仪器的展宽导致实际晶面的衍射曲线半高全宽测量值变大(如双晶衍射条件下Si单晶(111)面半高全宽约为12′′[18]).除此之外,晶体在切割过程中因为设备和加工工艺的原因不可避免会导致晶体表面与实际晶格产生一定的偏差,偏离角从精度较高的秒量级到较差的度量级均存在,这个偏离即晶面与实际表面之间的夹角(asymmetry angle).当存在晶面偏角时,实际光线的入射与晶格结构的关系如图1所示.

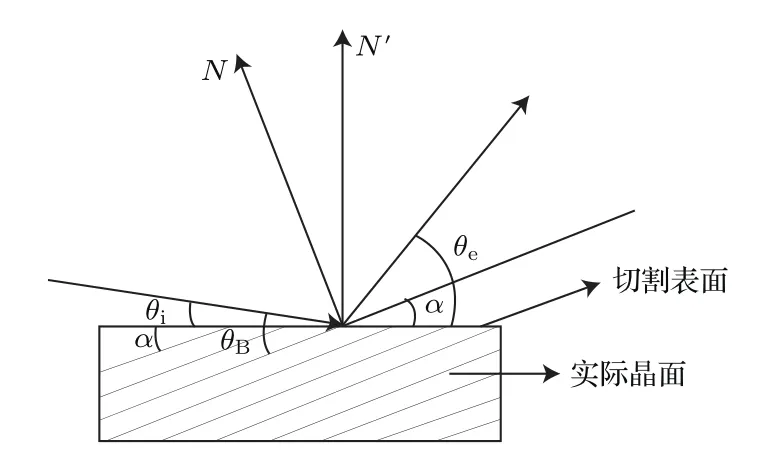
图1 具有一定偏离角的晶格结构示意图Fig.1.The schematic diagram of asymmetrically cut crystal.

图1中N为真实晶格表面的法线,N′为实际切割表面法线,θi为入射光与切割表面夹角,θe为出射光与切割表面夹角,α为切割表面与实际晶面夹角,θB为晶体的布拉格角.晶面偏角与入射光存在如下对应关系:

根据衍射动力学,有晶面偏角的晶体衍射的X射线反射束的半高全宽可以表示为

其中γ0,γg分别为入射X射线光束和反射X射线光束与晶片表面法线的方向余弦:

3 实验及结果

实验中选取了Czochralski法生长的Si(111)单晶作为实验材料,为了能够接近理想单晶状态,选取缺陷尽可能少的Si单晶,位错密度应该小于103/cm−2.材料的切割采用沈阳科晶仪器厂生产的STX-602型金刚石线切割机,最小切割厚度为0.1 mm.将Si单晶沿着(111)面切割,通过改进切割机的样品台,可以控制样品晶向角度到30′′以内,分别切割出20 mm×20 mm见方的五块Si单晶片,厚度控制在1.5 mm,不能过小,否则后续工序将会影响偏离角的准确性.样品上盘后在双轴研磨机上用标号分别为W40,W20,W10,W5,W3.5的碳化硅磨料进行研磨,通过粗磨到精磨的流程去除掉切割损伤,并逐步减少表面及亚表面损伤层.随后使用纳米SiO2抛光液在进口罗门哈斯抛光垫上进行粗抛和精抛处理,抛好的Si单晶在布鲁克Veeco轮廓仪上进行面型和粗糙度的测定,同时用原子力显微镜(AFM)进行对比测试,具体结果如图2所示.

图2 Veeco轮廓仪和AFM粗糙度检测结果Fig.2.The surface and roughness results of Veeco and AFM.

Veeco轮廓仪结果显示抛光后的硅片表面达到超光滑水平,无划痕,粗糙度Ra在3–4 Å左右(125µm×94µm),AFM测试结果(10µm×10µm)为2.04 Å左右,接近完美晶体表面水平.精密抛光后的样品在Bede公司生产的D1高精度X射线衍射仪上进行衍射曲线的测试(图3),波长为Cu靶的Kα线,该衍射仪具有锗和硅两块晶体单色器,在高分辨模式下(high resolution mode),通过8次反射得到单色性非常好的X射线.

图3 双晶X射线衍射示意图Fig.3.Schematic diagram of double crystal diffraction.

探测器面积为1cm2,单色器后设置0.05 mm宽狭缝,以进一步阻挡出射光源中的杂散光,获得更小的发散度,也能使晶体的垂直接收效率尽可能地接近1,提高测量的准确性.首先利用布拉格衍射精确测定了晶面偏角以及不同晶面偏角条件下的Si单晶摇摆曲线如图4所示.

经过测定,五块样品抛光后的角度偏离分别为0.008°,0.374°,0.749°,1.187°和5.306°. 图4中理论衍射曲线的晶面偏角是按实测的单晶Si样品进行计算的,实测值和理论曲线走势一致,由于测量过程中采样点数量原因,实测曲线的非对称性略小于理论计算值.曲线半高全宽随着晶面偏角的增大而减小,由于偏角的逐渐增大,入射角度和衍射角度的差值也在不断增加,衍射曲线的不对称性很明显地表现出来.同时X射线在晶体中的行程不断变化,在吸收的作用下峰值反射率随之下降[20].为后续应用Voigt函数法进行晶格应变测量,我们用探测器扫描方式针对不同晶面偏角的Si单晶样品进行了衍射曲线测量,作为对比,在实验过程中也用X射线衍射测量了不同研磨抛光阶段的衍射曲线以比较半高全宽的变化情况.具体见图5.

图5(a)是具有10.751°晶面偏角的样品在研磨和粗抛后衍射曲线对比,可以看出研磨阶段的半高全宽(223′′)远远大于抛光阶段,这是因为在切割、研磨过程中会在晶体的表层内产生裂纹、位错等缺陷[21−23],同时伴有一定程度的相变和晶粒细化,不可避免地出现亚表面损伤层,这将影响到晶体镶嵌结构中晶粒的大小及分布,也将会产生不同的应力效果[24],从而直接影响晶体的衍射曲线峰形和半高全宽.对于没有晶面偏角的晶体同样如此,图5(b)中是两块具有不同晶面偏角的样品在研磨和抛光阶段的半高全宽值对比,一块偏角为10.751°(图中标为Asy-cut 10.751°),另一块为0.008°(标为Sym-cut 0.008°), 后者可以视作无晶面偏角样品.二者作为同种材质在相同工艺条件下半高全宽的变化规律相一致,由于晶面偏角相差约10°,前者的半高全宽小于后者.从大小的绝对值可以看出,研磨阶段所带来的衍射曲线宽化是非常惊人的(超过200′′).因此消除晶体制作过程中的缺陷使晶体尽可能地接近完美晶体,才能使所测量的曲线更接近于本征衍射曲线.

图4(a)不同晶面偏角晶体衍射理论计算值;(b)不同偏角摇摆曲线实测值Fig.4.(a)The calculated rocking curve under different asymmetrical angles;(b)the measured value of rocking curve under different asymmetrical angles.

图5(a)研磨和抛光条件下衍射曲线对比(10.751°偏角);(b)晶面偏角为10.751°和0.008°(无偏角)的Si(111)单晶在粗磨、精磨、粗抛、精抛四种不同情况下衍射曲线半高全宽的变化Fig.5.(a)Diffraction curves under grinding and polishing with 10.751°asymmetrical angle;(b)the plots of full width at half maximum with asymmetrical angles of 10.751° and 0.008° under four different surface states.

表1 不同晶面偏角下Si(111)衍射曲线峰型实测数据与应变值Table 1.The measured data of Si(111)rocking curves with different asymmetrical angles.

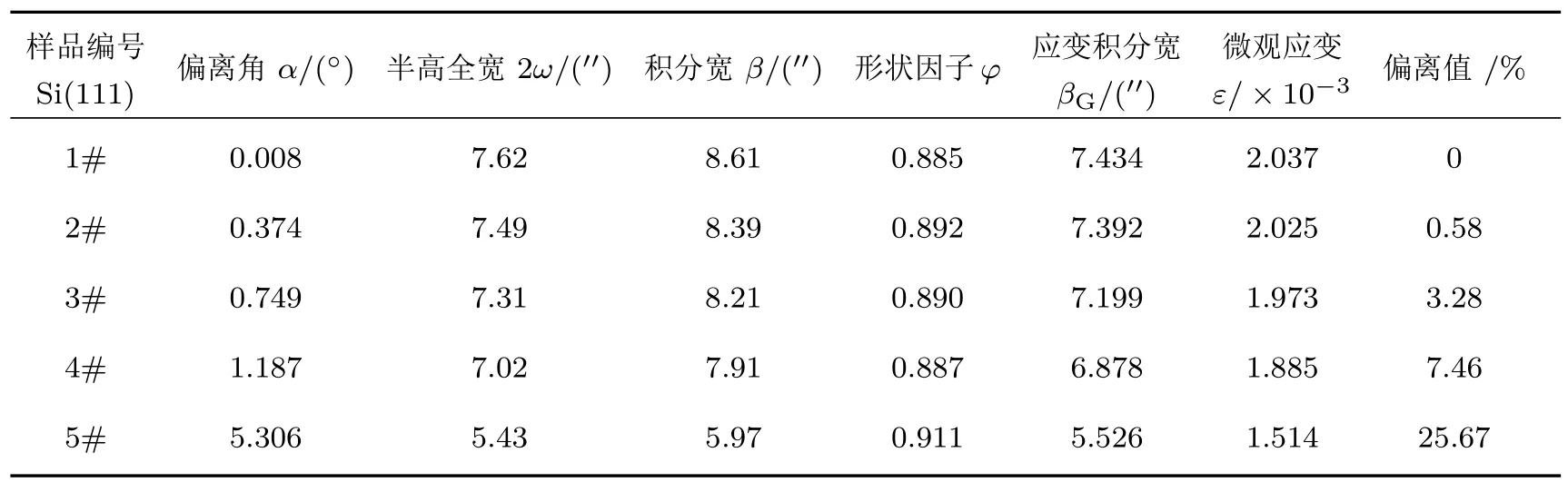
表2 不同晶面偏角下Si(111)衍射曲线峰型理论计算数据与应变值Table 2.The theory data of Si(111)rocking curves with different asymmetrical angles.

根据所测量晶体的衍射曲线峰型数值(表1),进行了拟合并计算了在不同晶面偏角情况下的半高全宽、积分宽度与应变值,其中应变偏离值是以0.008°(视作无偏角)时的应变作为零偏离如表2所列.

从表2的理论计算值可以看出,随着晶面偏角的增大,微观应变值随之减小,当偏离角达到1.187°时,理论计算出的应变相较于0.008°偏角(视为零偏角)的应变值小了7.46%.实际测量值也比零偏角数值小了6.81%,表现出相同的规律.无论是理论计算还是实际测量,当偏离角超过5°时,应用Voigt峰型函数法计算晶体内部微观应力应变将会有超过20%的误差.实际上,国内外利用衍射曲线峰型计算微观应力应变本身并不会产生这么大的误差,研究应变均是默认晶体本身为无晶向偏角的单晶,在没有考虑晶面偏角的情况下这种计算方法的误差在2.5%以内[25].由于Voigt峰型函数分析法需要用到衍射曲线的半高全宽和积分宽度,而这两项物理参数对晶面偏角非常敏感,因此如果忽略切割加工时所产生的偏角影响,当偏角大于1°时,计算结果的偏差将会大于5%以上,此时的实验数据超过可允许的误差范围.具体的半高全宽值和晶格应变偏差随晶面偏角的变化趋势如图6(a)所示.

在前面的理论分析中,晶格应变可视作衍射角的微变量与布拉格角正切的函数之积,对比公式ε= Δθ·ctg(θB)和ε=βG/4tgθB,二者具有相似之处.因此,除了Voigt函数法计算晶格应变,本文尝试用晶面偏角的非对称因子代替Voigt函数法中的Gauss分量积分宽度βG做近似处理,估算晶格应变大小.应用Voigt函数法计算出的理论值和实测晶格应变偏差与应用近似处理的数据如图6(b)所示.蓝色三角形数据为用非对称因子近似处理的应变偏差,和Voigt函数法相比,偏角为1°以内时相差不大可以替换.当晶面偏角增大到5.306°时,其计算出的晶格应变偏差达到43.33%,远远偏离Voigt函数法所得数值25.6%和29.7%,不再适用.

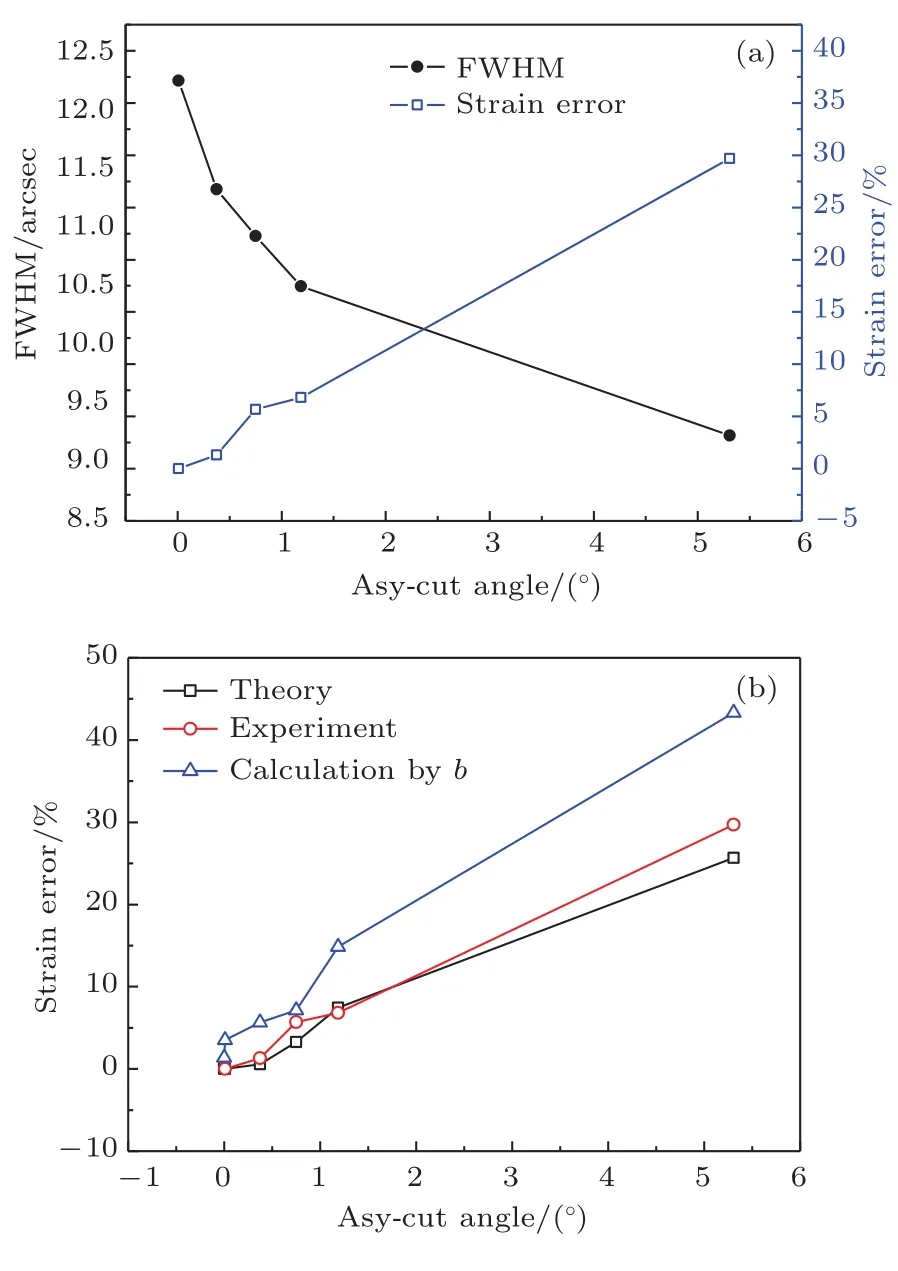
图6(a)不同晶面偏角下半高全宽值与应变误差之间的关系;(b)应用Voigt函数法得到的理论结果、实验数据与非对称因子计算数据对比Fig.6.(a)Plots of full width at half maximum vs.calculated stain error with different asymmetry angles;(b)comparison among theory data obtained by using Voigt function,measured data,and calculated values by asymmetry faction.

4 分析与讨论

根据理论计算,完美晶体在有晶面偏角和无偏角时晶体衍射曲线半高全宽相差系数实验中无偏角的Si(111)单晶在研磨抛光后,其衍射曲线半高全宽值为12.27′′,代入系数计算出晶面偏角为10° 时样品半高全宽为5.19′′,实测为6.76′′,与理论相符得比较好,说明抛光后的晶体接近理想单晶状态.而其他状态下的衍射曲线半高全宽最小都有27.56′′(粗抛),甚至到粗磨状态的223′′(如图5所示),特别是在研磨阶段,半高全宽非常大以至于有晶面偏√角与无晶面偏角的样品之间不再满足理论系数b之差,此时晶粒带来的展宽超过了晶面偏角的影响,已不能用衍射曲线半高全宽去测量晶格应变.通过研磨抛光工艺去除掉样品表面的损伤层以及亚表面损伤层,消除晶粒细化与缺陷所造成的衍射峰展宽之后,测量得到的晶体衍射曲线半高全宽基本为本征半高全宽,而晶面偏角成为影响峰宽的主要因素.应用Voigt函数法研究晶格应变可以看出,当晶面偏角超过0.7°时,理论计算应变偏差值达到3.28%,实际测量数据计算结果达到5.68%,况且实验和计算过程中还存在其他误差,也就是说如果希望计算结果偏差在5%以内的话,晶面偏角至少需要小于0.5°.因此,根据不同晶面偏角的Si单晶进行理论计算和实验测量可以看出:

1)晶体X射线衍射曲线半高全宽对晶面偏角非常敏感,Si(111)单晶的理论计算表明,在近完美状态下,晶面偏角从0°增加到0.5°,衍射曲线半高全宽值减小5.12%;对于其他相关物理研究,如需应用衍射曲线半高全宽数值时,必须考虑偏角的影响或尽可能减小晶面偏角;

2)晶面偏角对采用Voigt峰型函数法分析晶体本征内部微观应变结果有很大影响,偏角在0.749°以上时计算出的应变值误差超过5%,如要精确定量计算ε值晶面偏角至少要小于0.5°;

3)应用Voigt函数法分析晶体本征内部微观应变时应该去除表面及亚表面损伤层,消除晶粒细化等缺陷带来的展宽,晶体必须进行研磨和抛光至近完美晶体状态;也可应用此方法研究晶体的切割损伤造成的应变(不研磨抛光,无晶粒细化展宽影响);

4)在晶面偏角不大于1°情况下研究晶格应变ε时,如果做粗略测算,可以用半高全宽值与非对称因子之积代入公式直接计算.

5 结 论

本文采用高分辨X射线衍射技术测量了在不同晶面偏角条件下Si单晶(111)的晶格衍射曲线,并应用Voigt峰型函数法计算了晶体本征内部微观应变,结果表明,当晶面偏角大于0.749°时,应变计算误差超过了5%,达到5.68%,因此应用Voigt函数法研究晶格应变必须考虑晶面偏角的大小.对其他涉及衍射曲线半高全宽值的应用问题同样需要考虑晶面偏角对物理参数的影响.

感谢中国科学院高能物理研究所郑雷副研究员给予的帮助和讨论!

[1]Zaprazny Z,Korytar D,Siffalovic P,Jergel M,Demydenko M,Mikulik P,Dobrocka E,Ferrari C,Vagovic P,Mikloska M 2014 Advances in X-Ray/EUV Optics and Components IX 9207 920701Y

[2]Guigay J P,Ferrero C 2016 Acta Cryst.A 72 489

[3]Yang D R,Fan R X,Yao H N 1994 Mater.Sci.Eng.12 33(in Chinese)[杨德仁,樊瑞新,姚鸿年 1994材料科学与工程12 33]

[4]Zhao B H,Chen D L 1991 J.Zhejiang Univ.-Sci.A 25 538(in Chinese)[赵炳辉,陈立登 1991浙江大学学报 25 538]

[5]Zhu N C,Li R S,Chen J Y,Xu S S 1990 Acta Phys.Sin.39 770(in Chinese)[朱南昌,李润身,陈京一,许顺生1990物理学报39 770]

[6]Cembali F,Fabbri R,Servidori M,Zani A 1992 J.Appl.Cryst.25 424

[7]Huang J Y,E J C,Huang J W,Sun T,Fezzaa K,Xu S L,Luo S N 2016 Acta Mater.114 136

[8]Sun Y,Wang S L,Gu Q T,Xu X G,Ding J X,Liu W J,Liu G X,Zhu S J 2012 Acta Phys.Sin.61 210203(in Chinese)[孙云,王圣来,顾庆天,许心光,丁健旭,刘文洁,刘光霞,朱胜军2012物理学报61 210203]

[9]Dickey E C,Drivid V P,Hubbard C R 1997 J.Am.Ceram.Soc.80 2773

[10]Yoshiike T,Fujii N,Kozaki S 1997 J.Appl.Phys.36 5764

[11]Ward Iii A,Hendricks R W 1997 Proceding 5th International Conference Residual Stresses Lynköping,Sweden,June 16–18,1997 p1054

[12]Suzuki H,Akita K,Misawa H 2003 Jpn.Soc.Appl.Phys.42 2876

[13]Langford J I 1978 J.Appl.Cryst.11 10

[14]Macherauch E,Wohlfahrt H,Wolfstieg U 1973 Hart.Tech.Mitt.28 201

[15]de Kerjser Th H,Langford J I,Mittemeijer E J,Vogels A B P 1982 J.Appl.Cryst.15 308

[16]Chang M,Xu S L 1993 Acta Phys.Sin.42 446(in Chinese)[常明,许守廉 1993物理学报 42 446]

[17]Chang M,Xing J H,Xu S L 1994 Mater.Sci.Technol.2 21(in Chinese)[常明,邢金华,许守廉 1994材料科学与工艺2 21]

[18]Xu S S,Feng D 1987 X Ray Diffraction Topography(Beijing:Science Press)p168(in Chinese)[许顺生,冯端1987 X射线衍衬貌相学(北京:科学出版社)第168页]

[19]Fan Q C 2012 Mater.Sci.2 106(in Chinese)[范群成2012材料科学2 106]

[20]Chen H F,Liu K J 2006 J.Changshu Institute Technol.20 39(in Chinese)[陈惠芬,刘克家2006常熟理工学院学报20 39]

[21]Wang C C,Fang Q H,Chen J B,Liu Y W,Jin T 2016 Int.J.Adv.Manuf.Technol.83 937

[22]Buchwald R,Frohlich K,Wurzner S,Lehmann T,Sunder K,Moller H J 2013 Energy Procedia 38 901

[23]Fukumori T,Futagami K,Kuroki K 2004 Jpn.J.Appl.Phys.43 8331

[24]Zhang Y X 2006 Ph.D.Dissertation(Dalian:Dalian University of Technology)(in Chinese)[张银霞 2006博士学位论文(大连:大连理工大学)]

[25]Langford J I,Wilson A J C 1978 J.Appl.Cryst.11 102