年金标准组合收益率与组合规模关系

■文／李斌 张娅萍

企业年金作为我国养老保险体系的第二支柱，在加强养老保障、提高退休人员生活水平方面发挥着重要的作用。截至2018年6月底，全国企业年金经历10余年发展总规模达到1.31万亿元。自《职业年金基金管理暂行办法》下发后，各省职业年金相关工作也正式启动，预计未来职业年金规模将获得较快增长。

公募基金规模与收益率之间的关系受到广大投资者的重点关注，与此类似，年金标准组合收益率与其规模之间的关系亦受到广大年金委托人及代理人的关注。根据人社部公开数据，从2012年底至2018年6月末，单一计划组合的平均规模由2.12亿元增长至3.59亿元，集合计划组合平均规模由3.57亿元增长至7.17亿元。

研究背景

分散化投资理论。在宏观经济下行的形势下，信用违约高发，且股票市场波动较大。分散化投资可对冲不同资产类别、不同行业个股、个券的投资风险从而减小组合波动，然而，规模较小的组合由于投资难以做到充分分散化，抵御市场风险能力受到更大挑战。

规模效应。组合规模大小直接影响年金管理机构的重视程度、管理费的优惠程度。在产品配置方面，规模较大的组合获得优质资产配置的机会更多。在投资团队配备方面，规模较大的组合更容易获得机构专业投资团队力量的投入，从而更好地发挥规模效应。

政策要求。当资金规模较低时，标准组合无法有效进入某些市场。银行间债券市场交易的特点为单笔交易量大，买卖成交面额一般不低于1000万元。而根据《企业年金基金管理办法》第五十条规定“单个投资组合的企业年金基金财产，投资于一家企业所发行的债券等资产，按照公允价值计算，不得超过该投资组合企业年金基金财产净值的10%”，意味着组合规模如果达不到1亿元，则无法进入银行间债券市场。

由于沪深两市新股网下合格投资者至少需要1000万元的市值，且目前在实践中发行人和主承销商事先确定的市值要求提高到6000万元。根据《企业年金基金管理办法》第四十八条规定“投资股票等权益产品以及股票基金、混合基金的比例，不得高于投资组合企业年金基金财产净值的30%”，意味着权益上限为30%的标准组合规模至少在4亿元以上，才能参与两市新股网下首次公开募集（IPO），获得较高无风险收益。

当前的研究基本上聚焦公募基金规模与收益率之间的关系，且无定论。有人认为基金规模总体上与基金业绩呈现一种负相关的关系，即基金规模越小其业绩越好，小盘基金业绩显著好于大盘基金业绩。也有人对我国开放式基金规模与业绩之间的关系进行了相关性分析及显著性检验，实证分析表明，开放式基金的规模与业绩之间并不存在某种特定的关系。还有人利用特征基准组合法（DGTW），通过实证检验发现，开放式股票型基金规模对基金选股能力、基金收益存在倒U型的影响，进一步得出我国股票型基金的最佳规模（资产净值）在4.98亿—23.48亿元之间。

当前的研究结果均以市场上公募基金为样本，但公募基金与年金标准组合在资金性质、运作模式、考核机制等方面有较大差别，本文将以A公司企业年金基金标准组合为样本，着重考察标准组合规模与收益率之间的关系。截至2018年上半年，A公司建立了197个标准组合，组合最大规模27.44亿元，最小规模0.27亿元，平均规模7.15亿元。

描述性分析

标准组合平均规模与其相对收益的关系（假设各投管人投资能力相同）。在运作满5年的170个标准组合中，选取43个权益仓位上限为20%—30%的标准组合（与实际仓位基本一致），为剔除市场对标准组合收益率的影响，将各标准组合的收益率除以A公司企业年金当年平均收益率得到标准组合相对收益。以相对收益为纵坐标，标准组合规模为横坐标，用43个标准组合当年平均规模和相对收益来制作散点图，并用Excel进行拟合，选取使得可决系数最大的趋势线。2013年的散点图及趋势线见图1：

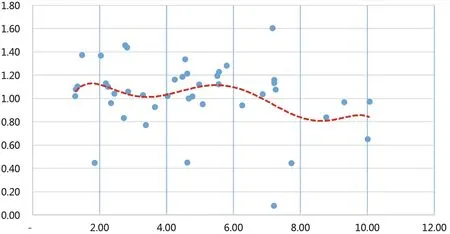
图1 2013年A公司年金权益上限在20%—30%之间的标准组合相对收益与规模散点图

由图1观察得到，2013年，标准组合规模接近1.75亿元，或者5.1亿元时，相对收益达到极大值。与此类似，2014—2017年每年的散点图也显示出相似的特征，比如：2014年，当标准组合规模为2.3亿元、7亿元、12亿元左右时，相对收益达到极大值；2015年，当标准组合规模为3.5亿元、11亿元左右时，相对收益达到极大值；2016年，当标准组合规模为3亿元、11亿元左右时，相对收益达到极大值；2017年，当标准组合规模为4亿元、11亿元、19亿元左右时，相对收益达到极大值。由于已经剔除了市场对标准组合收益率的影响，可以将上述2013—2017年的数据作为截面数据分析，显示出，当规模在2.5亿元、13亿元左右时，相对收益达到极大值。

综上，当控制标准组合权益上限在20%—30%且剔除市场因素的影响时，可以得到以下结论：使得可决系数最高的拟合趋势方程为一元六次线性方程，即至少存在两个规模使得收益率达到极大值。具体来看，当标准组合规模在2亿—5亿元时，相对收益率达到一个极大值，当标准组合规模在10亿—13亿元时，相对收益率会出现另一个极大值，该极大值往往会超过前一个极大值达到最大值。随着时间推移，随着组合规模自然增长，2013—2017年的峰值在右移。从波动角度出发，当标准组合规模较小时，组合收益率的波动、尤其是向下波动的程度较大。

标准组合平均规模与组合相对收益的关系（假设各投管人投资能力不同）。在实践中，不同投资管理人的投资制度、投资风格差异较大，一定程度上影响了组合收益率。因此，在这一部分，假设各投资管理人投资能力不同，但同一投资管理人不同投资经理的投资能力相同。将2013—2017年215组数据按照投资管理人进行分类，M基金、N养老、O养老的样本量大于等于30， M基金管理标准组合的规模与收益散点图见图2：

从图2可以看到，当把投资管理人的投资能力考虑进去以后，出现两个峰值的趋势更为明显。对于M基金所管理的标准组合，规模大于2亿元后，相对收益率提升，在4亿元时达到极大值，后下降。在规模约为10亿元时达到极大值，后下降。N养老、O养老所管理的标准组合规模与收益之间也呈现出类似的规律，对于N养老所管理的标准组合，当规模为2亿元、4亿元、10亿元时，相对收益率达到极大值。对于O养老，当规模为5亿元、15亿元左右时，标准组合相对收益率达到极大值。

2017年组合平均规模与超额收益率的关系。随着A公司企业年金运营管理进一步精细化、系统化，从2017年起考察各标准组合各类资产的全年平均仓位与收益率情况。2017年A公司运作满年度的标准组合为197个，将各组合的收益率进行调整，在每个标准组合收益率中剔除2017年中证100收益率乘以该组合股票平均持仓、2017年中债总全价指数收益率乘以该组合市值计价类固收资产平均持仓、A公司企业年金所持成本计价类资产2017年平均收益率乘以该组合成本计价类资产平均持仓、A公司企业年金所持混合型养老金产品2017年平均收益率乘以该组合混合型养老金产品平均持仓，以及A公司企业年金所持流动类资产2017年平均收益率乘以该组合流动类资产平均持仓，得到组合的超额收益。

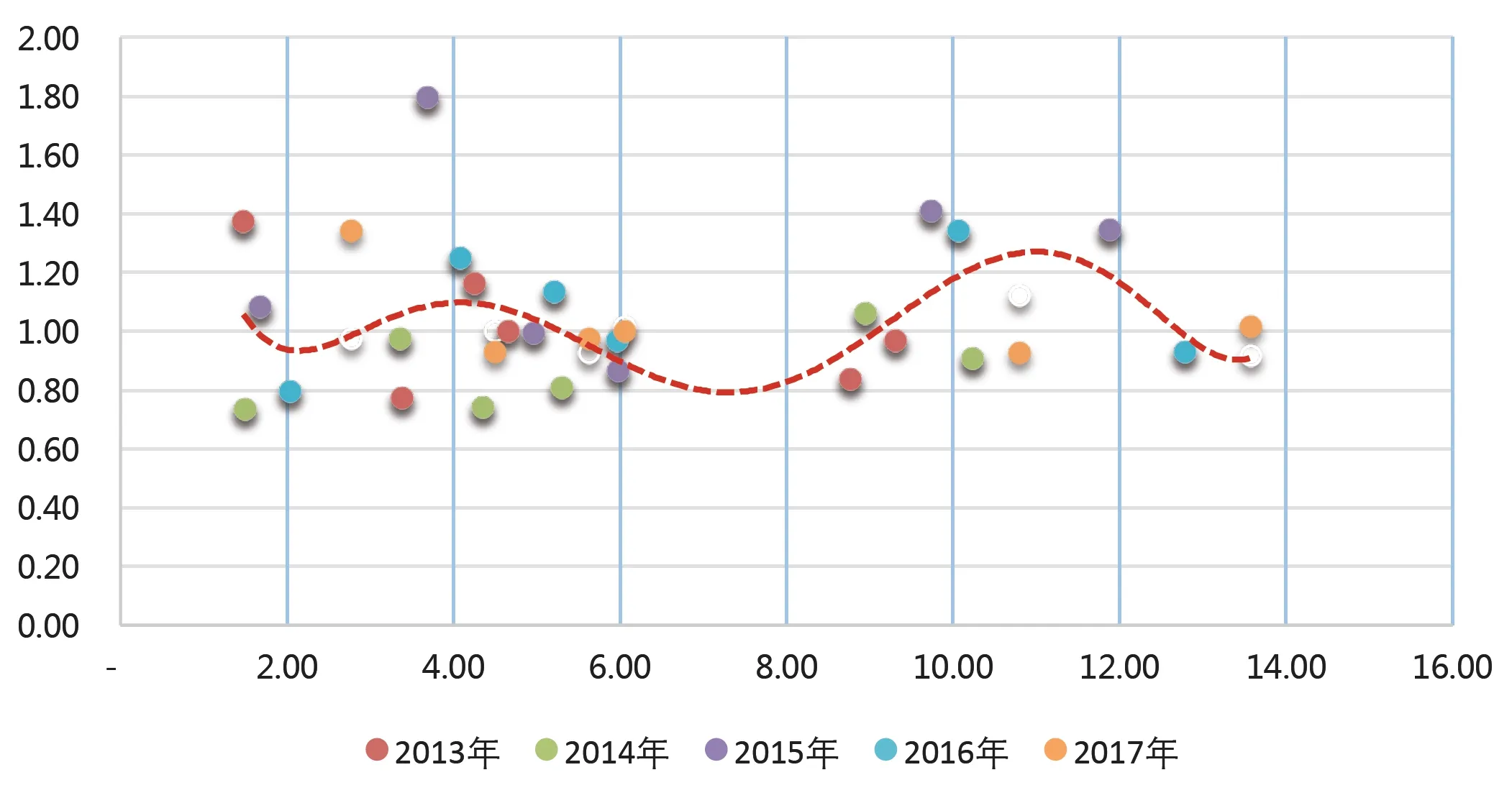
图2 2013—2017年A公司年金权益上限在20%—30%之间且投管人为M基金的标准组合相对收益与规模散点图

将197个标准组合收益率调整为超额收益率后，既剔除市场对组合收益率的影响又剔除策略对组合收益率的影响，通过描述性统计的方法得出结论：组合规模与收益率的关系不是简单的线性或倒U型关系，面对较多的不确定性因素，基本符合存在两个极大值的趋势。第一个极大值的出现是由于组合规模2亿—5亿元能够顺利参与各市场，此时相对收益率会达到极大值。下一个极大值的出现则将会在10亿元以后。

实证分析

根据上述分析，组合收益率与组合规模的六次方、当前资本市场情况、组合的投资策略、投资管理人的管理能力有关。因此本文选取恰当变量，建立回归模型。

样本选取。本文选取A公司2017年运作满年度的197个标准组合作为研究样本。

变量选取。在考虑标准组合平均规模对收益率的影响外，还应当考虑2017年的资本市场情况、组合投资政策、投资管理人投资能力等因素，所选取的自变量为标准组合2017年累计收益率r，因变量包括标准组合2017年权益资产平均仓位乘以2017年中证100指数收益率stock、标准组合2017年市值计价类债券平均仓位乘以2017年中债总全价指数收益率bond、标准组合2017年混合型产品平均仓位乘以2017年A公司所有标准组合混合型养老金产品平均收益率hybrid、标准组合2017年成本计价类资产平均仓位乘以2017年A公司所有标准组合成本计价类资产平均收益率alternative、标准组合2017年流动类资产平均仓位乘以2017年A公司所有标准组合流动类资产平均收益率money、标准组合的投资管理人所管理的A公司全部组合2017年平均收益率除以A公司企业年金基金2017年收益率score以及标准组合2017年平均规模的六次方scale6。

模型假设。本文旨在考察企业年金标准组合收益率与规模之间的关系，根据描述性统计部分分析，假设标准组合规模的六次方对组合收益率有显著影响。

模型建立。本文建立多元线性回归方程如下：

ri=ai+b1stocki++b2bondi+b3hybridi+b4alternativei+b5moneyi+b6scorei+b7scale6i+ei

其中： ri为组合i2017年累计收益率； stocki为组合i2017年权益资产平均仓位乘以2017年中证100指数收益率；bondi为组合i2017年市值计价类债券平均仓位乘以2017年中债总全价指数收益率；hybridi为组合i2017年混合型产品平均仓位乘以2017年A公司所有标准组合混合型养老金产品平均收益率；alternativei为组合i2017年成本计价类资产平均仓位乘以2017年A公司所有标准组合成本计价类资产平均收益率；moneyi为组合i2017年流动类资产平均仓位乘以2017年A公司所有标准组合流动类资产平均收益率；scorei为组合i的投资管理人所管理的A公司全部组合2017年平均收益率除以A公司企业年金基金2017年收益率；scale6i为组合i2017年平均规模的六次方, ui为随机项。

模型结果。本文使用stata做模型回归，回归结果如下：

ri=0.0331**+0.303***stocki+0.720**bondi- 0.264hybridi- 0.0655alternativei- 0.182moneyi+0.0253****scorei+7.33e-11*scale6i+ei

其中：*在10%的显著性水平下显著，**在5%的显著性水平下显著，***在1%的显著性水平下显著，****在0.1%的显著性水平下显著。

从模型结果可知，标准组合规模的六次方在10%的显著性水平下，显著影响组合收益率，且本模型不存在多重共线性。

结论及建议

通过上述分析，可以得到如下结论：标准组合规模对组合收益率的影响不是简单线性或者倒U型，而是在10%的显著性水平下，标准组合规模的六次方显著影响组合收益率。当组合规模在2亿—5亿元时，由于能够达到市场准入资格，所以收益率达到极大值。当组合规模超过10亿元时，由于对于投资管理人来说引起足够重视，组合收益率会出现另一个极大值，该极大值往往会超过前一个极大值达到最大值。标准组合规模较小时，由于组合投资资产分散化程度较低，风险无法充分对冲，因此组合收益率的波动性较大。

建议在年金资产实际投资运作过程中，资金分配不宜过于分散，分配给各标准组合的规模不宜过小，初期至少各组合应满足进入各市场的最低门槛，后期随着组合规模逐渐增大，也会使得投资管理人倾斜更大资源。当然也可考虑使用集约化程度更高的养老金产品进行投资，较小的资金量就可参与规模可观、收益良好、充分分散、投资管理人倾注资源更多的优秀养老金产品，在申购赎回、调整配置策略、更换投资管理团队方面更为灵活。■