剖析学生物理解题误区的策略

陈建忠

（普宁市梅峰中学，广东 普宁）

物理学不仅充满了趣味性，也是一门实用性很强的自然学科，很多学生从初步接触物理学科阶段就知道学好物理的必要性和重要性，但是物理确实让人头疼，不少学生反映物理很难学，具体表现为“一听就懂，一看就会，一做就错”。当然，学生觉得难学的确是有很多原因的，但是在解题时容易陷入误区也是一个不容忽视的重要原因。搞清学生解题误区的具体表现和原因，这对于提高学生的解题能力，提高教学质量是有所帮助的。笔者根据自己长期的教学工作实践经验，针对排除学生解题误区提出以下观点：

一、排除干扰，滤取有用信息

其实有时候题目看似给出了很多的条件，实则在解题过程中并不是必需的，有些可能就是命题者设置的陷阱或者是故意干扰，有些则是题目的“引子”，因此学生在解题时要准确识别各个条件的作用，找出与问题真正有关的条件，排除干扰。例如：

短跑运动员在100 m竞赛中，测得8 s末的速度为9.4 m/s，10 s末到达终点的速度是10.2 m/s，求运动员在全程内的平均速度。

【小结】解题时不要只是简单地类比平时接触过的相似题目，生搬硬套解题模板。这要求学生对于物理概念和规律的特征、适用范围、思维方式等有一个清析的认识，因此，在教学过程中，让学生领会一些科学的思维方法，在领会这些方法时，不是将其当作知识向学生灌输，而应注意在“潜移默化”中逐步渗透，使学生真正掌握知识，应用自如，方能摒弃干扰，滤取有用信息。

二、注意理清物理问题中的临界状态，避免陷入误区

临界状态就是当某种物理变化从一种现象变化为另一种现象，或者某个物体从一种状态转变为另一种状态时，发生的这种质的飞跃的转折状态。临界问题能有效考查学生多方面的能力。因此，很多的物理问题都设置在这种临界状态下，是解决问题和转变思路的关键所在，但是又往往很隐蔽，不容易被发现，稍不留神就容易解错题。例如：

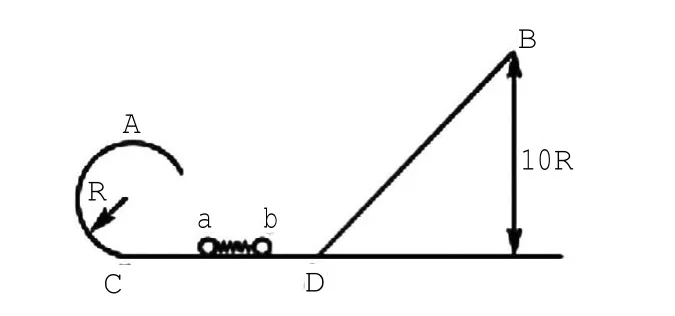
如图所示，半径为R的光滑圆环轨道与高为10R的光滑斜面安置在同一竖直平面内，两轨道之间由一条光滑水平轨道CD相连，在水平轨道CD上一轻质弹簧被两小球a、b夹住（不连接）处于静止状态，今同时释放两个小球，a球恰好能通过圆环轨道最高点A，b球恰好能到达斜面最高点B，已知a球质量为m，求释放小球前弹簧具有的弹性势能为多少。

【错解】设这两个小球释放时的速度分别为va、vb，弹簧的弹性势能为Ep。

【正确解答】设这两个小球释放时的速度分别为va、vb，弹簧的弹性势能为Ep。

a球正好能够通过圆环轨道的最高点A需要满足：mag=

对a、b球组成的系统，根据动量守恒定律得：0=mava-mbvb④

由①～⑤联立解得：Ep=7.5 mgR

【小结】许多学生对题意“a球恰好能通过圆环轨道最高点A”不理解，造成无法求解，类似题目叙述中出现一些特殊词语如“恰好”“刚好”“最大”“最高”“至少”这就是临界问题。所以，在解决这种问题时，要认真审题，分析系统的物理过程，尤其是要注意对临界状态的分析，找出问题的转折点，抓住起承上启下作用的物理量，准确锁定临界点，只要抓住这一关键，问题的解决就会事半功倍。

总之，教师只有通过分析和总结学生在解题过程中出现误区的原因，切实从学生的实际出发进行教学，在紧扣课程标准的前提下精选一些有典型性和针对性的习题，在课堂中给学生示范和启发，既把应试中所要解决的问题转移到课堂上来，也避免了“题海战术”，能够收到以少胜多的成效。从而让学生把书本知识掌握得更扎实，让课堂教学更精彩。