初中几何证明的典型错误及其应对策略
□海南省东方市八所中学 吴东翔
初中平面几何的学习是几何学的入门学习。若学生掌握该学科的学习方法,则会激发他们对数学学科的学习兴趣。因此培养学生自觉、主动地探求平面几何的解题问题,不仅是铸造学生优质的思维品格的基础、是培养学生严密的逻辑推理能力的有效途径,也决定着学生往后能否向更广更深的领域学习,关系着学生的成长发展。为了让学生的数学基础牢固,提升他们的逻辑推理能力,在几年的教学中,我观察到了学生在学习初中几何的种种情况。如,平面几何学习中几何证明是学生的痛点,几何证明问题往往让学生理不清头绪,不知如何下手,久而久之,学生对几何证明产生畏惧心理,对几何的学习也失去兴趣。“几何证明难”是学生不想学平面几何的原因,要想从源头上解决问题,我们必须找出问题的根源,以问题为主线,通过对问题的研究分析,寻找出现问题的原因,从而“对症下药”,寻找解决问题的方法,使教师的教学引导更加高效,学生的学习更加科学,为学生获取更多的“数学素养”、为学生未来的发展奠定基础。
一、典型错误
经过多方面的经验积累及调查分析,总结出几何证明的典型错误主要表现在以下几点:
1.概念定理,理解不透。
(1)学生对几何的概念、判断定理的识记与理解流于表面,容易忽略定理的内在含义,在应用时不考虑它的适用条件和范围。
在线段的垂直平分线的性质学习中,学生没有完全理解“线段垂直平分线上的点到线段两个端点的距离才相等”的内在条件,在证明时,容易出错。
例:如图,在△ABC中,AB=AC,点D是BC的中点,求证:(1)△ABD≌△ACD ;(2)BE=CE。
错误分析:对于(2)的证明,很多学生都认为D是BC的中点,所以BE=CE,没有去探讨DE是BC的中垂线。
(2)在三角形全等的证明中,按照题目给出的已知条件,很多学生都会找出“边边角”的条件,然后就直接利用“边边角”直接得出两个三角形全等了,错误原因就是“无中生有,自创定理”。
2.隐含条件,不善挖掘。
在初中几何证明中,有一些题目,证明结论所需要的已知条件,不是直接给出来的,而是隐含的。对于这类题目,如果学生不善于挖掘这些条件,就没有足够的条件逐步推导出结论。这类题目学生共同的感觉就是“缺少条件”。
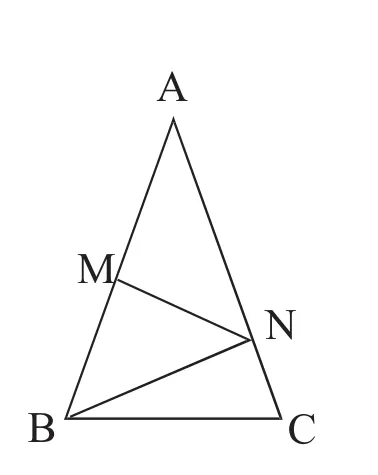
例:如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点N,交AB于点M,求证:△ABC∽△BCN。
分析:本题的关键在于抓住∠A=36°,AB=AC这
两个已知条件,由∠A=36°,AB=AC可得到∠ABC=∠C=(180-36)/2=72°,进而就可得所要证明的结论。但在实际证明中,很多学生都没有挖掘出这个隐含条件,所以结论也就无法求证。

3.推理混乱,缺乏规范。
表达混乱,条理不清是属于证明过程书写不规范的问题,对于初学者来说,这种现象尤为常见。这种现象,常见的有两种:
(1)不知如何下笔,是学生觉得“几何证明难”的共同心病,拿到一个几何证明题目,学生看了,心里明白怎么得到需要证明的结论,但下笔书写时,不知怎么表达推理过程或者推理混乱,逻辑不严密。
(2)几何证明的书写要求有它的独特性:书写表达必须规范,然而在几何证明中,学生表达不规范比比皆是。常见的情况有前因后果逻辑推理不严密、画图不规范、几何符号语言应用不规范等等。
4.添线助证,无从下手。
众所周知,很多几何题的证明,往往利用原图现有的“线”是难于证明的,这就需要添加辅助线。添加辅助线可以使复杂的几何证明问题变得简单,然而,因为没有掌握添加辅助线的要领,证明时,没有找到证明的突破口,题目也就无法得证。添加辅助线解决几何问题是几何证明的一大技巧,题目需要添加辅助线辅助证明时,学生没有找到添加辅助线的切入口,因此无法进行解题,这也是学生解决几何问题感到“无从下手”的原因。
5.文字命题,茫然无策。
在教学中,学生最难于应对的是文字命题的证明,对于此类问题,学生无法理解命题的含义,未能从中找出命题的题设和结论,不仅如此,学生还难于根据题意规范画图、不懂得用几何符号语言写出已知条件和求证。
6.生活问题,不善建模。
数学是来源于生活,又为生活服务的一门学科,生活中的很多现象,我们都可以把它归纳为数学问题,并用数学思维进行解决,然而,对于现实生活中的实际问题,学生往往不能把它进行建模,把生活问题转化为数学问题。几何尤其如此,学生没有耐心理解实际问题和数学的关系,没有更好地把实际问题归纳成几何问题,没有更好地画图加以直观理解,从而就没有达到解决实际问题的目的。
二、应对策略
以上是初中几何教学中学生证明常见的几类典型错误,在教学中如何有效应对呢?通过思考探索和与同伴探讨交流,总结出以下几点体会:
1.夯实基础、强化应用。
学生几何解题一切错误的原因都是基础不扎实,如果基础扎实了,而不善于应用,那就是平时缺少解题应用训练。在平常教学中,老师必须帮助学生理清几何定义、几何定理、公理条件和结论之间的逻辑思维关系、掌握应用范围,在解题实践中,放手让学生大胆尝试,要知道“只有让学生在实践中发现自己解题存在的不规范及漏洞错误,学生才能体会深刻及更好纠正”。“夯实基础、加强应用”是学生熟练运用的基础,也只有基础夯实,学生对几何的学习才更有兴趣,学生对学好几何才更有信心。
2.深入挖掘,突破瓶颈。
几何证明中,综合题目都有“瓶颈”,题目中设置的“瓶颈”往往让学生找不到解题的突破口,如果“瓶颈”突破了,学生证明也会豁然开朗,有一种“柳暗花明又一村”的感觉,此时的学生会无比兴奋,也会很享受那种成就感,这给学生学习几何带来多大的兴趣啊!何乐而不为呢?然而,几何证明中的“瓶颈”如何突破呢?课堂教学中必须做好以下几点:
(1)培养学生认真阅题、审题的良好习惯,在审题中能充分挖掘题目中的显性和隐性已知条件的意识。几何结论的证明,碰到最多的问题就是“结论的推导缺少条件”,然而题目给的条件肯定是足够的,有显性的,也有隐性的,只是学生不善于挖掘或利用而已。只有充分利用题目中的显性和隐性已知条件,结论的证明才能顺利推导出来。
(2)引导学生逆向分析,证明几何问题时,要让学生懂得从要证明的结论开始,逆向分析,结论的得出需要哪些条件,再从题目中去寻找这些条件,逐一突破。
(3)几何结论的证明,学生心里往往明白由这些条件可以得出这个结论,但要书写时却不知如何下笔。对于这样的问题,在教学中我们可以让学生多模仿例题的书写过程,让学生多尝试,学生之间相互纠正,这样他们体会到的知识会更深刻。
(4)几何文字命题的证明,学生的难点是:①无法找出命题的题设和结论,即找不出已知条件和需要证明的结论;②画简图,不懂得用几何符号语言写出已知和求证,针对这样的情况我们可以采取“化整为零,逐一突破”的策略。即要让学生懂得把问题分成几个步骤:第一,理清题意,画出草图;第二,根据题目中的条件和结论,用几何符号写出已知和求证;第三,从已知条件开始,逐一规范写出推导过程。
(5)数学文化的精华就是“化为数学”和“数学化为”,生活中的几何问题,要把它化为数学问题去求解,需要学生有良好的“建模”能力,在教学中,我们要注重数学“建模”思想的参透,多设置生活实例让学生练习,老师和学生一起探讨如何把“生活问题”化为“数学问题”之间的过渡关系。
3.方法归纳,形成思维。
方法归纳需要多思考,只有多思考才能找到不同问题的解决规律,例如添加辅助线证明问题时,不同类型的题目有不同的添加方法,但它们是有规律的,需要老师引导学生多思考、多体会、多总结。在几何证明的训练中,教师要多引导、帮助学生进行解题方法、解题技巧及分析思路的整理和归纳,只有这样,学生才能把老师的分析思路、解题技巧和证明思维转变为自己的方法,也就是要让学会收“渔”而不是收“鱼”,学生才能更好地开启几何证明的智慧之门。
解决问题的对策是很多的,在教学实践中,师生只有“持之以恒”,“几何证明难”的问题才能有效解决。

