型材拉弯成形过程的参数化有限元建模方法

张学广

（中车长春轨道客车股份有限公司工程规划发展部，130062，长春∥工程师）

近年来，型材因其具备重量轻、强度高及成形性好的优势，在轨道交通车辆车体结构件中得到了广泛使用［1］。拉弯工艺是型材的主要成形方式，成形效果与拉弯过程中的加载参数密切相关。受材料、工艺及设备等众多因素的影响，成形后型材常出现截面畸变、扭曲及精度不足等缺陷［2-4］。在实际生产中，工件试制之前一般多通过数值仿真方式进行工件成形模拟，以达到先期预测工件成形缺陷的目的，并针对性地调整工件拉弯成形工艺参数［5］。因此，拉弯成形过程的有限元模型的准确性与适用性，对于分析工件的成形效果具有决定性作用。

1　型材拉弯成形

型材实际生产中多选用张壁式拉弯机，主要结构包括工作台、机架、双侧转臂、拉伸缸、夹钳等，其结构如图1所示。张壁式拉弯机原理是将拉弯胎固定在工作台上，依靠拉弯机两侧转臂旋转带动型材绕模具转动，实现工件成形。在进行拉弯时，首先将型材放在台面上，两端由夹钳夹紧，启动拉伸缸，型材开始进行预拉伸，达到屈服极限；随后进行包覆拉伸，转臂在油压缸拉杆作用下绕台面开始旋转，实现边拉伸边弯曲；最后机床上的液压缸停止运作，型材只在拉伸缸的作用下进行补拉。

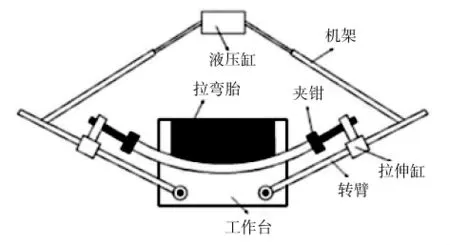
图1　张壁式拉弯机结构示意图

2　型材拉弯建模方法

在型材成形过程的有限元模拟中，多采用预拉-弯曲-补拉（P-M-P）方式将工件的成形过程分解为3个独立的阶段，通过调控夹钳的轨迹实现型材拉弯成形［6］。在整个成形过程的仿真中，只需要根据工件目标形状、预拉量、补拉量3个参数即可计算出每个阶段结束时夹钳的空间坐标，并结合夹钳的拉伸速度和转臂旋转速度实现整个成形过程中夹钳轨迹的跟踪［7-8］。

这种方式的优势是可适用于不同目标形状和尺寸的型材成形，只需通过几何尺寸计算即可获取加载轨迹，建模过程简便。然而，此方式和型材的实际生产加工方式存在一定差别。首先，在P-M-P方式分析中，型材弯曲阶段只发生纯弯曲，忽略了弯曲贴模过程中夹钳的拉伸作用，而实际生产中夹钳对型材作用为边弯曲边拉伸；其次，P-M-P方式分析一般假定夹钳的拉伸和旋转中均为匀速加载，而实际生产中，型材在弯曲贴模阶段，为减小卸载回弹量，多根据工件的圆弧半径设定非均匀的拉伸量和旋转量，这种工况会导致P-M-P方式分析中夹钳轨迹计算及其复杂［9-10］。

由于P-M-P方式分析中夹钳的运动轨迹和实际生产中夹钳的运动轨迹存在一定差异，导致有限元模拟的精度难以保证。因此，建立一种便捷、精确的参数化有限元模型，对于型材拉弯成形效果的分析和预测具有重要意义。

3　拉弯成形参数化模型

以轨道交通车辆车顶弯梁作为研究对象，采用有限元模拟方式预测工件拉弯后成形缺陷，并优化主要工艺参数。工件的目标形状和截面形状如图2所示。由图2可以看出，工件为对称结构，由两段曲率半径不同的圆弧和延长段组成。工件材质为SUS301LN不锈钢。如图3所示，工件主要成形缺陷为拉弯后型材截面缩口和帽檐翘曲，这些缺陷给后续的车体骨架组配工作带来较大困难。生产中主要依赖调控拉弯过程中的型材变形量，以降低工件的回弹，并减小截面畸变。

本文采用有限元分析软件Abaqus建立了型材拉弯的有限元模型，如图4所示。模型中采用了梁单元简化拉弯机的转臂，梁一端铰接，为了避免模拟中梁单元的变形，在材料属性赋予时设置一个较大的弹性模量。模型中将夹钳简化为刚体壳，夹钳中心点和梁共线。在夹钳中心点和梁另一端建立转换器连接。使用转换器连接单元的主要优势是可以保证在整个成形过程中夹钳的运动始终沿转臂方向，不受转臂运动的影响，从而可以实现贴模过程中型材的边拉边弯。

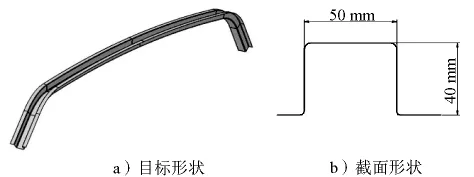
图2　车顶弯梁工件的目标形状

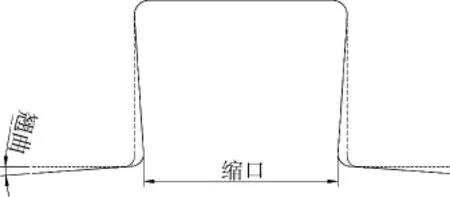
图3　车顶弯梁工件的主要成形缺陷

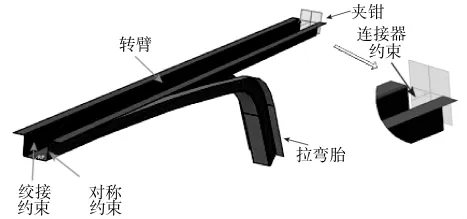
图4　车顶弯梁工件的拉弯成形有限元模型

在有限元仿真中，使用梁的旋转等效拉弯机转臂的运动，使用连接器单元的运动等效夹钳的运动。则有限元模型中，只需设置梁的转角和连接器的位移两个参数，无需计算夹钳在整个成形过程中的空间坐标。

4　模型验证

为了验证本文建立的型材拉弯成形过程参数化有限元仿真模型的适用性和准确性，选用P-M-P方式分析的仿真结果及试验结果与参数化有限元模型仿真结果进行对比。在有限元模拟中设置了不同的拉弯工艺参数，并对比了工件成形后的成形缺陷。

由于实际生产中主要依赖调控拉弯过程中的拉伸量抑制产品的工艺缺陷，因此在有限元模拟中，依据生产经验，设置了4组不同的拉伸量。并以成形后工件的回弹量、缩口量和翘曲量作为量化指标。不同拉伸量下的工件成形后的工艺缺陷如表1所示。

由表1可以看出，随着拉伸量的增加，工件成形后的塑性变形量增加，工件成形后的回弹量呈现降低趋势，同时，工件的缩口量和翘曲量均增加。有限元模拟结果和试验结果呈现一定的差异。文中定义了偏差比δi，用于衡量仿真结果的准确性：

表1　不同工艺参数下车顶弯梁工件拉弯工艺缺陷

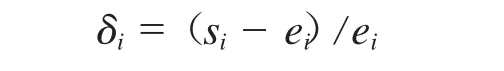
式中：

si——工艺参数为i的仿真结果；

ei——工艺参数为i的试验结果。

对上述偏差比进行数理统计可知，P-M-P方式的仿真结果平均偏差比为28.9%，参数化模型的平均偏差比为10.8%。结果表明：相比于采用P-M-P模型进行型材拉弯成形仿真，采用本文中提出的参数化模型可以降低仿真偏差，模拟结果更接近试验结果。

5　结语

提出了一种基于连接器单元的型材拉弯成形模拟方法，通过定义型材拉弯过程中的伸长量，实现了拉弯过程中的边拉边弯有限元模式。相较于传统的P-M-P模型，该模型可以避免有限元建模过程中夹钳轨迹的计算，简化了有限元仿真模型的建立过程。以轨道车辆车顶弯梁为例，采用该模型验证了不同工艺参数下工件的成形效果，仿真结果和试验数据贴合。本项研究成果在结构件制造领域具有一定的工程应用价值。

［1］金朝海，周贤宾，刁可山，等.铝合金型材拉弯成形回弹的有限元模拟［J］.材料科学与工艺，2004，12（4）：394.

［2］CLAUSERN A H，HOPPERSTAD O S，LANGSETH M.Stretch bendingofaluminumextrusions：Effectofgeometryandalloy［J］.JournalofEngineeringMechanics，1999，125（4）：392.

［3］王胜满.用于地铁车辆的不锈钢型材拉弯成形缺陷［J］.吉林大学学报（工学版），2013（6）：1546.

［4］谷诤巍，刘化民，刘玉梅，等.不锈钢型材拉弯成形工艺模拟研究［J］.模具工业，2006，32（8）：42.

［5］刘志军，金朝海，李东升，等.基于PSBPD的T型材拉弯夹钳加载轨迹设计及有限元模拟［J］.塑性工程学报，2012，19（6）：109.

［6］李小强，周贤宾，金朝海，等.基于有限元模拟的三维型材拉弯轨迹设计［J］.航空学报，2009，30（3）：544.

［7］李小强，周贤宾，金朝海，等.型材拉弯数值模拟夹钳边界条件的一种等效模型［J］.塑性工程学报，2009，16（1）：64.

［8］刘天骄，王永军，夏晓娇，等.型材拉弯数值模拟轨迹建模方法［J］.锻压技术，2014，39（7）：132.

［9］HOPPERSTAD O S，LEIRA B J，REMSET H S，et al.Reliability-based analysis of a stretch-bending process for alumini-m extrusions［J］.Computers&Structures，1999，71（1）：63.

［10］金朝海，周贤宾，谷诤巍，等.基于位移控制的型材2D张臂式拉弯加载轨迹设计及数控代码生成［J］.塑性工程学报，2009，16（2）：66.