某新型动车组网侧电流谐波特性测试分析

赵海波

（中车长春轨道客车股份有限公司总体研发部，130062，长春∥高级工程师）

随着高铁运行里程的大幅增长，高铁列车与接触网之间的供电耦合关系特别是高铁列车的网侧电流谐波对整个牵引供电系统的影响日益明显。在武广高铁、京沪高铁等客运专线开通运行时，均发生过因动车组网侧电流谐波原因造成接触网供电异常并导致事故发生等情况，因此，有效控制动车组的网侧电流谐波质量对高铁列车安全运行有着重要的意义。本文通过对某新型动车组的网侧电流谐波测量和计算，阐明在应用谐波抑制的措施后，该动车组的网侧电流谐波含量符合相关要求，同时对其牵引特性未产生影响，满足动车组运用的要求［1-2］。

1　动车组网侧电流谐波分析

图1为动车组单牵引单元主电路图。由于在牵引变流器中使用了大量电气电子元件，因此造成了较宽的谐波频谱（3～200 Hz）。因有大量的动车组在同时运行，很容易引起动车组和接触网供电之间的谐波振荡，在特定频段引发谐波电流共振及谐振过电压，最终导致动车组和牵引供电设备被击穿和烧毁的事故。因此，必须对动车组的谐波进行有效的控制。

图1　动车组单牵引单元主电路图

动车组变流器器件开关频率的限制及整列动车组的四象限整流器的配合控制是解决谐波问题的重点和难点。目前，通常采用以下两种方式处理该问题［3］：

（1）在硬件电路上通过三电平方式或者设置谐波滤波器的方式降低谐波；

（2）在变流器控制软件控制策略上采用基于平均电流反馈、基于原边电流反馈两种优化的瞬态电流控制策略和多重四象限载波移相控制技术等方式降低谐波。

硬件电路和软件控制策略两种处理方式在工程实践中往往均被采用，以达到最经济和最优良的控制效果［4-5］。

2　计算方法

2.1　网侧电流谐波计算方法

2.1.1网侧电流频谱分析

网侧电流可以用以下周期函数来表示［6］：式中：

k——不为0常数；T——函数周期。

将式（1）展开为一个收敛的傅里叶级数

其中：

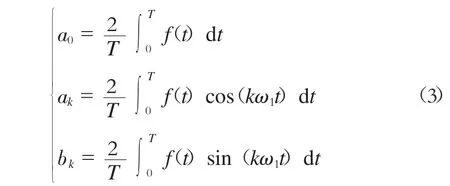
式（2）可进一步简化为

其中：

先根据式（3）计算 a0、ak、bk，再将其代入式（5）中求得A0、Akm，最终得到网侧电流的频谱。

2.1.2等效干扰电流计算

等效干扰电流计算公式如下［11］：

式中：

JP——等效干扰电流，A；

In——n次谐波电流有效值，A；

Sn——国际电报咨询委员会规定的杂音评价系数。

2.1.3功率因素计算

功率因素计算公式如下：

式中：

λ——功率因素；

U——网侧电压有效值，kV；

I——网流有效值，A；

P——网侧有功功率，kW。

2.2　轮周牵引力计算

2.2.1加速度法

瞬时加速度按下式计算［8-9］：

式中：

a——瞬时加速度，m/s2；v0、v1——瞬时速度，m/s；

t——动车组从v0加速到v1所用的时间，s。

根据各速度下的瞬时加速度，计算该速度下的加速力为：

式中：

F0——动车组加速力，kN；

a——瞬时加速度，m/s2；

m——动车组定员质量，t；

γ——动车组回转质量系数，通常取0.06。

动车组轮周牵引力为：

式中：

F——动车组轮周牵引力，kN；

W0——基本运行阻力，kN。

基本运行阻力一般采用下式计算：

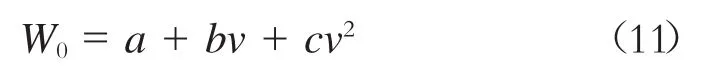
式中参数a、b和c根据动车组车型确定。

2.2.2电功率法

动车组轮周牵引力按式（12）计算［10］：

式中：

N——动车组牵引电机总台数，N=16；

n——被测电机台数；

Pi——第i台牵引电机有功功率，kW；

v——被测动车组瞬时速度，km/h；

ηm——速度v对应的电机效率，取0.947；

ηg——机械传动效率，取0.975。

3　线路试验

3.1　试验方法

试验正式开始前，动车组已持续运行不少于30 min，以使轴温及各运转部分状态接近实际运用状况。动车组以满级牵引和满级制动工况运行，运行时对各工况数据进行连续采样［11-12］。

3.2　试验设备

3.2.1数据采集设备

数据采集设备采用工业级测试模块。模块工作温度为-45～+85℃（允许结露），配置16或24个电压、电流采集通道，最高采样率频可达到200 kHz，主机内置128 G固态硬盘，通过以太网实现数据传送［13］。

3.2.2电压和电流传感器

采用的电压传感器共有两种。电机电压采用高压差分探头，量程可达±7 000 V，需单相220 V电源给适配器供电。另一种为无源电压传感器，量程可达±200 V，用于测试动车组网压压互二次侧电压。交流电流采用无源开合式电流互感器，量程为0～1 000A，精度等级均可达0.5级。

3.3　试验记录

试验记录以下数据：列车网侧电压，V；列车网侧电流，A；列车速度信息，km/h；牵引电机输入电压，V；牵引电机输入电流，A。

4　试验结果分析

4.1　网侧电流谐波特性

4.1.1满级牵引工况

动车组在平直轨道起动加速到350 km/h。动车组起动后网流平稳上升，直至动车组进入恒功率阶段，此时网流稳定在460 A上下，拐点速度大约为160 km/h，谐波成分中3次谐波含有量最高，但是含有率不超过0.6%。图2为动车组在此过程中的网侧电流有效值曲线及其频谱。

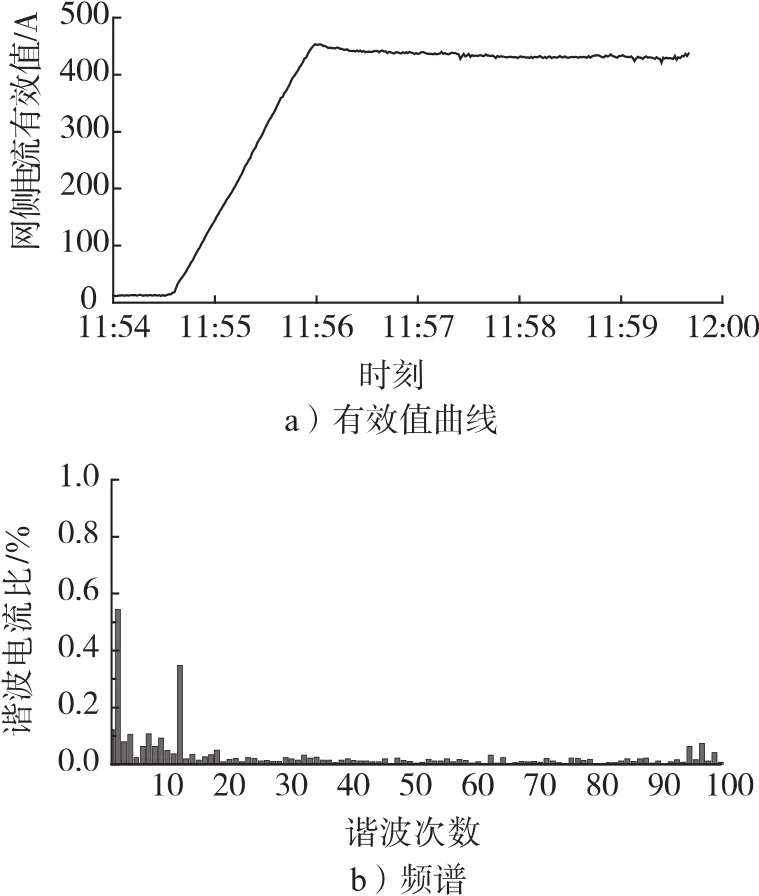
图2　网侧电流有效值曲线及其频谱

动车组在牵引过程中，功率因素随着取用有功功率的增大而变大，即功率发挥越大，功率因数越高（见图3）。功率发挥超过5 MW时，功率因数达0.98以上。

图3　功率因数与取用有功功率的关系

图4为动车组网侧电流总谐波畸变率、等效干扰电流与取用功率的关系曲线。网侧电流有效值越大（牵引功率越大），网侧电流总谐波畸变率越低。功率发挥超过5 MW时，网侧电流总谐波畸变率在3%以下，等效干扰电流在1.5 A以下。

4.1.2满级制动工况

图4　牵引工况下总谐波畸变率、等效干扰电流与取用功率的关系

图5　网侧电流有效值曲线及其频谱

图5为动车组在制动过程中的网侧电流有效值曲线及其频谱。动车组制动前速度为350 km/h，在15∶52∶22 开始制动后，动车组网侧电流突然变大，并保持在400 A上下波动，此时为恒功率制动。当速度减小到160 km/h后，随着再生制动功率的减小，网侧电流平稳下降直至动车组停止。谐波成分中3次谐波含有量最高，但含有率不超过0.8%。

由于动车组在制动过程中向牵引网反馈能量，故功率因素是负的，如图6所示。但是，与牵引过程相一致，功率因素绝对值随着取用有功功率的增大而变大，即功率发挥越大，功率因数越高。功率发挥超过5 MW时，功率因数达0.98以上。

图6　功率因数与取用有功功率的关系

图7　制动工况下总谐波畸变率、等效干扰电流与取用功率的关系

图7为动车组制动过程中网流总谐波畸变率、等效干扰电流与取用功率的关系曲线。网流有效值越大（制动功率越大），网流总谐波畸变率越低。制动功率超过5 MW时，网流总谐波畸变率在3%以下，等效干扰电流在1.5 A以下。

4.2　牵引特性

牵引特性分为两个区，即恒力矩区和恒功率区，如图8所示。在恒力矩区牵引力随着速度升高缓慢下降，这与动车组的黏着特性随速度变化趋势是相适应的。在高速区，因受电机电压或功率所限，输出功率基本不变，牵引力随速度升高而呈双曲线关系下降。恒功率区的起点大概为160 km/h。

5　结语

新型动车组采用移相技术有效地控制了谐波，无论处于牵引工况还是制动工况，功率超过5 MW时，网侧电流谐波成分都很低，各次谐波含有率不超过1%，网侧电流总谐波畸变率在3%以下，等效干扰电流在1.5 A以下，功率因数在0.98以上。因此，该新型动车组满足运用要求。

图8　动车组牵引特性曲线

［1］曹建猷．电气化铁道供电系统［M］．北京：中国铁道出版社，1983：23．

［2］王晖，吴命利．电气化铁路低频振荡研究综述［J］．电工技术学报，2015，30（19）：70．

［3］杨栋，王思明，许建玉．CRH3型动车组牵引制动模式曲线的算法研究［J］．城市轨道交通研究，2013，16（12）：94．

［4］李强.电气化铁路车网电气匹配问题［J］．电气化铁道，2014，25（3）：13．

［5］杨少兵，吴命利．基于实测数据的高速动车组谐波分布特性与概率模型研究［J］．铁道学报，2010，32（3）：33．

［6］LEE H，LEE C，JANG G，et al.Harmonic analysis of the Korean high-speed railway using the eight-port representation model［J］．IEEE Trans on Power Delivery，2006，21（2）：979．

［7］何正友，胡海涛，方雷，等．高速铁路牵引供电系统谐波及其传输特性研究［J］．中国电机工程学报，2011，31（16）：55．

［8］孟志强．高次谐波对牵引网保护的危害及改进措施［J］．电气化铁道，2006，17（增刊 1）：131．

［9］周晶杰，文秧林．动力分散型动车组牵引特性的在线测量［J］．电力机车与城轨车辆，2014，37（4）：54．

［10］朱颖，吕希奎，许佑顶.动车组牵引计算与仿真系统［M］．北京：中国铁道出版社，2015：56.

［11］王正，潘高强．三相逆变电源输出电压的谐波抑制综合方法［J］．电气技术，2010（1）：89.

［12］张民，何正友，胡海涛，等．高速动车组再生制动下网侧电流谐波特性分析［J］．电网技术，2012，36（9）：257．

［13］郭蕾，李群湛，解绍锋，等．交-直-交高速动车组机车的谐波模型及仿真分析［J］．系统仿真学报，2012，24（5）：943．