非同轴两轮机器人的自平衡分析与控制策略

李亚锋 ，王卫军 ，2，张 弓 ，侯至丞 ，杨 根

（1.广州中国科学院先进技术研究所，广州 511400；2.深圳中科德睿智能科技有限公司，深圳 518109）

两轮平衡机器人是载人移动机器人领域的研究热门之一，有同轴两轮（左右布置）和非同轴两轮（前后布置）两类。同轴两轮机器人采用被动平衡方式，即需要依靠前后运动来实现动态平衡（类似倒立摆系统），已取得很多研究成果和应用如大名鼎鼎的Segway[1]。非同轴两轮机器人是一个欠驱动、非线性、侧向不稳定系统，其动力学与控制研究极具挑战性，目前仍处在实验室研发阶段[2]。1998年俄罗斯莫斯科国立大学，利用陀螺效应产生的进动力矩实现侧平衡，设计了一款具有自平衡功能的自行车[3]。2005年日本村田公司推出了会骑自行车的“村田男孩”，依靠安装在其胸部的一个垂直惯性轮实现左右平衡[4]。2011年美国LIT汽车公司，申请了利用2个飞轮的陀螺效应来保持平衡的载人摩托车专利[5]。2014年美国俄亥俄州立大学以拉格朗日方程建立系统动力学方程，设计一阶滑模控制器并在自行车上开展试验，具有较好的鲁棒性[6]。

与同轴两轮机器人相比，非同轴两轮机器人具有动作灵活，良好的爬坡和越障能力，安全性好等优点，有望应用于载人交通工具、自主巡逻、侦查等领域。目前非同轴两轮机器人车仍面临一些技术问题：平衡鲁棒性欠佳；抗撞击能力弱；高速行驶、小半径转向、爬坡等运动的稳定性不高[7-8]。在此，介绍一种载人非同轴两轮自平衡机器人，依靠一对陀螺转子同步进动产生的陀螺力矩实现自平衡。

1 原理与结构

单个陀螺转子进动产生的陀螺力矩τ，如图1所示，满足的公式[9]为

式中：Jz为陀螺转子的转动惯量；ωz为陀螺转子自转角速度；ωy为陀螺转子进动角速度。陀螺力矩的方向符合右手定则（即图中x轴负方向），并随进动角的变化而变化。

图1 陀螺转子陀螺效应原理Fig.1 Gyroscopic effect principle of gyro rotor

由于进动角的存在，陀螺力矩可分解为翻滚力矩和航向力矩，前者是起平衡作用的有效力矩，后者则是影响平衡稳定的干扰力矩，因此单陀螺平衡的效果很差。文中所采用双陀螺平衡的结构如图2所示。为了使两陀螺转子的翻滚力矩作用叠加、航向力矩相互抵消，应保证两陀螺转子的自转方向和进动方向都相反。

由图可见，车身机体坐标系O1x1y1y1，陀螺转子坐标系O2x2y2z2和陀螺转子坐标系O3x3y3z3这3个坐标系处于同一平面内（即y1，y2，y3轴的方向相同，由纸面朝外），其中x1轴为车身前进方向。为便于分析，令2个陀螺的进动角速度大小相等、方向相反。假设某刻两陀螺的进动角为α，则双陀螺转子进动过程中在x1轴方向产生的翻滚力矩τro为

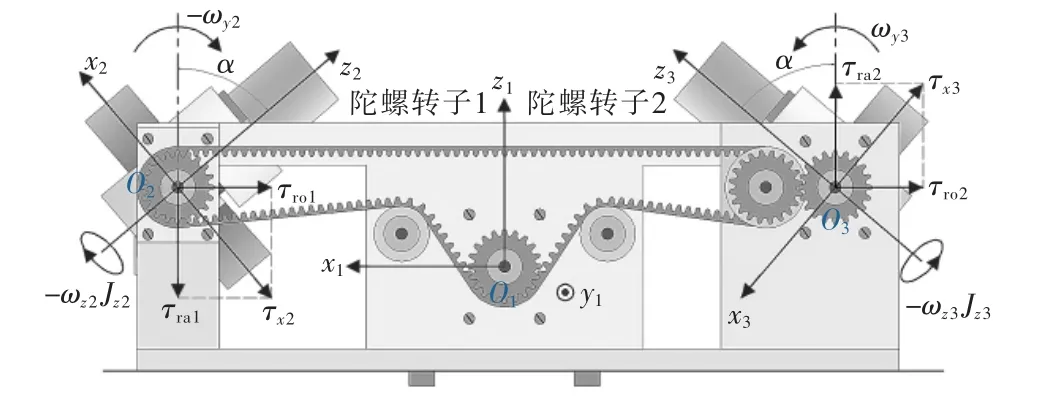
图2 陀螺装置平衡机理分析Fig.2 Analysis of balance mechanism of gyroscope

式中：Jz2，Jz3为陀螺转子的转动惯量；ωz2，ωz3为陀螺转子自转角速度；ωy1为陀螺转子进动角速度。翻滚力矩τro的方向为x1轴负方向。2个陀螺在z1轴方向产生的航向力矩τra为

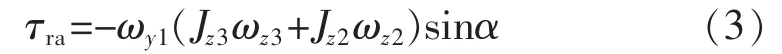
由上式可知，当两陀螺结构参数一致且进动速度大小相同时，航向力矩为零，因此双陀螺装置的优势在于，可以抵消因单陀螺进动而产生的干扰力矩，实现系统的平衡稳定。为保证两陀螺转子进动过程的同步性，平衡装置采用了机械方式即同步带传动机构。由此可知进动角速度与进动角是控制系统平衡的关键因素。

为进一步简化分析过程，假设机器人的前、后轮与地面的接触点都落在地理坐标系xyz的x轴上，且机体坐标x1与地理坐标x轴平行，其动力学模型为如图3所示。在忽略空气阻力、轮胎与地面之间力矩的前提下，当车身相对于z轴的倾斜角为θ时，平衡车动力学方程为

式中：Jx为车身相对于x轴的转动惯量；θ¨为车身左右倾斜的角加速度 （即翻滚角加速度）；G为机器人所受重力；h为重心与O点的距离。

图3 系统简化力学模型Fig.3 Simplified mechanical model of system

非同轴两轮自平衡机器人机械结构的实物如图4所示，其整体结构由车头、车尾、车身3部分组成。车头部分包括橡胶轮、舵机与前轮转向机构等；车尾部分主要轮毂电机、减震机构等；车身包括双陀螺平衡装置与电控系统。双陀螺平衡装置由前后陀螺转子、无刷电机、陀螺转子同步机构、陀螺进动电机等构成。电控系统由主控制板、电机驱动器及传感器、锂电池组等构成。

图4 非同轴两轮自平衡机器人Fig.4 Non coaxial two wheel self balancing robot

2 平衡控制方案

非同轴两轮自平衡机器人的控制系统硬件组成如图5所示。控制系统按功能分为5个单元，即上位机、主控单元、驱动器、传感器检测、电源管理。电机包括4种类型：陀螺自转电机、陀螺进动电机、前轮转向舵机、后轮前进驱动电机。

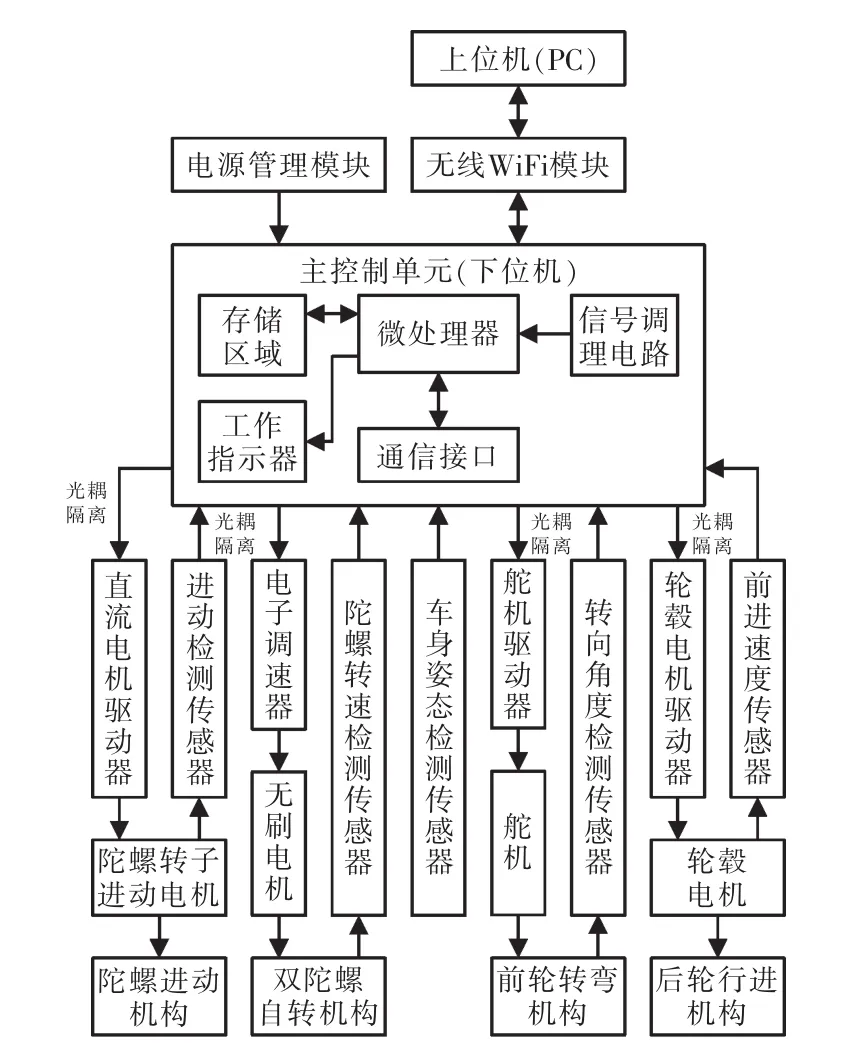
图5 控制系统硬件组成Fig.5 Hardware composition of control system

自平衡机器人系统最重要的参数是车身倾斜角θ。要实现平衡应使θ=0。单纯的PD控制可以使车身实现短暂的平衡，但无法持续稳定，系统容易震荡直至崩溃。究其原因，自平衡机器人是一个非线性、耦合的系统，而且为了抵抗车身外力矩（主要是重力矩）的存在，陀螺始终会朝一个方向进动，从而导致进动角过大，陀螺效应的平衡作用失效。

在平衡控制过程中，系统需要添加1个陀螺进动角归零补偿量θα，使陀螺进动角α趋向于零，否则车身会因陀螺效应失效而倾倒[10]。文中采用了模糊PD与增益调度来控制机器人的自平衡过程，如图6所示。平衡控制器通过增益调度来减小车身左右震荡，而这些参数值均由试验测试得到。

图6 非同轴两轮机器人的平衡控制Fig.6 Balance control for non coaxial two wheeled robot

由日常经验可知，以一定的速度驾驶自行车或摩托车转弯时，车身需要倾斜一定角度才能保证转弯不倒，这是因为转弯过程中需要车身提供一个向心力。考虑到该转弯因素，车身的左右动力学方程（4）变为

式中：Fc为车身转弯时产生的离心力。而转弯时，车身倾斜角θ与转弯角β之间的关系[11]为

式中：v为车身前进速度；d为前后轮胎着地点之间的距离；g为重力加速度；m为车身质量；M为总质量（加上负载）；L为车身重心高度。

为解决转弯时的平衡问题，PD控制中需要再加入1个基于转弯离心力的倾角补偿量θβ（其大小与前轮转弯角和后轮转速相关）。

车身倾斜角的总补偿量为θα+θβ，由此得到车身倾斜角的偏差为

式中：θd为期望的倾斜角；θe为倾斜角总补偿量。

那么，通过模糊PD控制器来控制前后2个陀螺产生的翻滚力矩为

式中：τro为前、后陀螺转子产生的总翻滚力矩；kP和kD为模糊PD控制器输出控制增益。

根据模糊理论，取倾斜角θ和倾斜角速度θ˙的模糊子集为｛NB，NM，NS，Z，PS，PM，PB｝。 根据模糊子集和自平衡机器人系统的动力学简化模型，模糊输入参数倾斜角误差eθ与角速度误差e˙θ的模糊论域为［-1，1］，量化等级为｛-1，0.5，-0.25，0，0.25，0.5，1｝，量化因子分别为0.3 rad和1 rad/s。模糊输出控制量的论域［-1，1］，量化等级为｛-1，0.5，-0.25，0，0.25，0.5，1｝，比例因子为10 rad/s。输入与输出隶属的函数如图7所示[12-13]。而模糊控制规则见表1。

图7 输入输出隶属度函数Fig.7 Input-output membership function

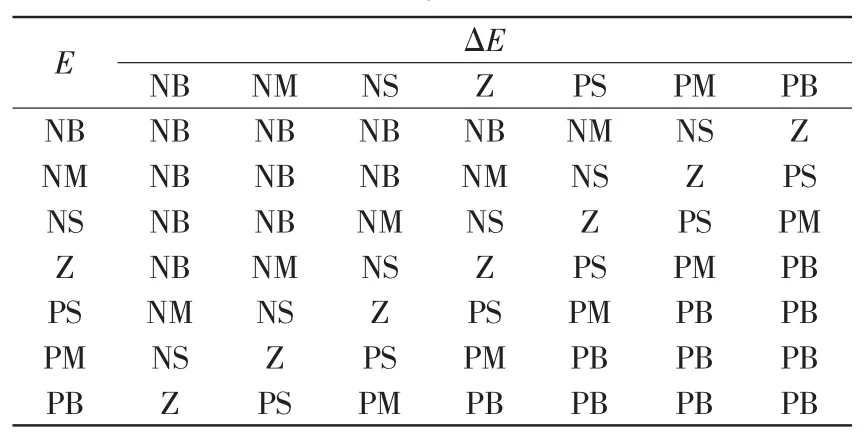
表1 模糊控制规则Tab.1 Fuzzy control rule

通过Matlab仿真，得到平衡机器人的动态数据时间响应曲线如图8所示，由仿真结果可以看出系统能够快速进入平衡稳定状态。

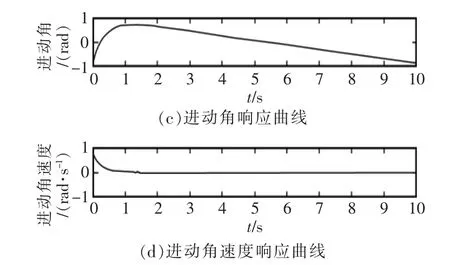
图8 车身自平衡过程中姿态参数响应曲线Fig.8 Response curve of attitude parameter in auto body self balancing process

3 试验与结果分析

文中针对非同轴两轮机器人的平衡性能开展了一些试验验证，分别采用PD和模糊PD增益调度方式在样机上进行了对比测试。试验样机的具体规格参数见表2，主控单元芯片采用ARM，数据采样率为100 Hz。

表2 系统规格参数Tab.2 System specification parameters

图9 车身自平衡过程中倾斜角及其角速度Fig.9 Tilt angle and its angular velocity in auto body self balancing

从静止倾斜倒地至自动恢复平衡过程中，车身的倾斜角与角速度变化曲线如图9所示。由图可见，车身刚开始处于左侧倾倒状态，由倾倒状态变成平衡状态只需要1～2 s内就可以完成。单纯采用PD控制方式只能使车身在平衡状态附近维持十几秒，然后很快出现高频震荡，直至系统崩溃倾倒在右侧。而采用模糊PD增益调度控制方式，能始终维持车身在平衡状态，超调量小且稳定状态下车身倾斜角θ为-0.02～0.02 rad，即偏差小于±1.5°。

在车身自平衡过程中，陀螺的进动角与角速度的变化曲线如图10所示。同样可见，当采用纯PD控制方式时，陀螺转子进动角在30 s时刻开始高频震荡直至陀螺力矩失效状态。而采用模糊PD增益调度方式时，陀螺进动角终态偏差处于-0.2～-0.1 rad，由图可见，陀螺进动角终态的偏差中心并未处于0线上，这是由于制作的样机重心偏向右侧形成偏心力矩所致，陀螺需要不断地朝一个方向进动来产生抵抗力矩。

图10 车身自平衡过程中陀螺进动角及其角速度Fig.10 Gyro precession angle and its angular velocity in auto body self balancing

4 结语

非同轴两轮机器人采用了主动平衡方式，具有良好的平衡鲁棒性、抗冲击性以及调速性，可在静止或移动中实现平衡，故安全性更好。所开发的非同轴两轮的载人交通工具原理样机能够实现自动平衡。由试验结果可知，非同轴两轮自平衡机器人采用纯PD控制平衡的效果并不理想，而采用模糊PD增益调度方式的平衡性能则表现很好，车身倾斜角与陀螺进动角都处在比较稳定、合理的范围内。

参考文献：

[1]“Segway”[EB/OL].http：//www.segway.com.

[2]朱磊磊，陈军.轮式移动机器人研究综述.机床与液压[J].2009，37（8）：242-247.

[3]Beznos A V，Formal'sky A M，Gurfinkel E V，et al.Control of autonomous motion of two-wheel bicycle with gyroscopic stabilization[C]//IEEE International Conference on Robotics and Automation.IEEE，1998，3（3）：2670-2675.

[4]村田制作所[EB/OL].http：//murata.com.

[5]丹尼尔·基勇·金，凯文·布莱特尼，安德鲁·L·曾.陀螺稳定式车辆：中国，80024268.3[P].2013-07-03.

[6]Yetkin H，Kalouche S，Vernier M，et al.Gyroscopic stabilization of unmanned bicycle[C]//American Control Conference（ACC）.IEEE，2014：4549-4554.

[7]Karnopp D.Tilt control for gyro-stabilized two-wheeled vehicles[J].Vehicle System Dynamics，2002，37（2）：145-156.

[8]李勇，耿建平，林群煦，等.基于双飞轮陀螺效应的两轮自平衡机器人的研制[J].机电产品开发与创新，2015，28（6）：14-16，28.

[9]周龙加.一种基于陀螺进动效应的稳定装置研制[J].现代制造，2016，21（24）：100-101.

[10]于法传.基于陀螺进动效应的独立机器人的研制[D].哈尔滨：哈尔滨工业大学，2015.

[11]张婷玉，陈清梅，邢红军.自行车转弯问题的研究[J].首都师范大学学报：自然科学版，2015，36（4）：30-32.

[12]杨正才，吕科.基于模糊PD控制方法的两轮直立自平衡电动车研究[J].控制工程，2016，23（3）：366-370.

[13]胡敬敏，阮晓钢.一种基于模糊控制理论的独轮机器人控制算法[J].控制与决策，2010，25（6）：862-866.