基于ROS的六自由度机械臂轨迹规划
刘 磊,宁 祎
(河南工业大学 机器人研究所,郑州 450007)
当前,机器人的功能越来越丰富,机器人系统更加复杂,机器人软件的编写复杂且繁琐,大量的冗余代码,复杂的建模,可移植性差的平台,功能层次性差,仿真的通用性差,等各种问题也显现出来。机器人操作系统可以很好地解决这些问题。基于ROS相关软件包,可以对各类型的机器人进行快速建模、仿真和控制[1]。在此,利用ROS搭建了1个六自由度机械臂的仿真平台,并在该平台下对六自由度机械臂的直线圆弧轨迹规划进行了实验。由实验结果可见,机械臂各关节运动轨迹平滑,末端位置精度满足要求。
1 机器人操作系统
1.1 ROS系统的整体框架
ROS系统是构建在 Ubuntu系统上的一种应用程序框架。它利用Ubuntu系统来获得对硬件的支持,同时在这个应用程序框架上有开发有多种的应用软件功能包[2]。ROS整合了许多工具包,如:系统可视化工具rqt,3D可视化工具Rviz,地图构建与导航工具SLAM,机械臂仿真包MoveIt!,等。在此,主要采用ROS的3D可视化工具Rviz和机械臂仿真包MoveIt!,构建了机器人仿真平台。
1.2 机械臂仿真包MoveIt!
MoveIt!是一款可用于正逆运动学求解、集成运动规划、感知检测等方面的机器人软件包[3]。在此使用它进行了运动学的解算和运动规划。MoveIt!的节点框架如图1所示。
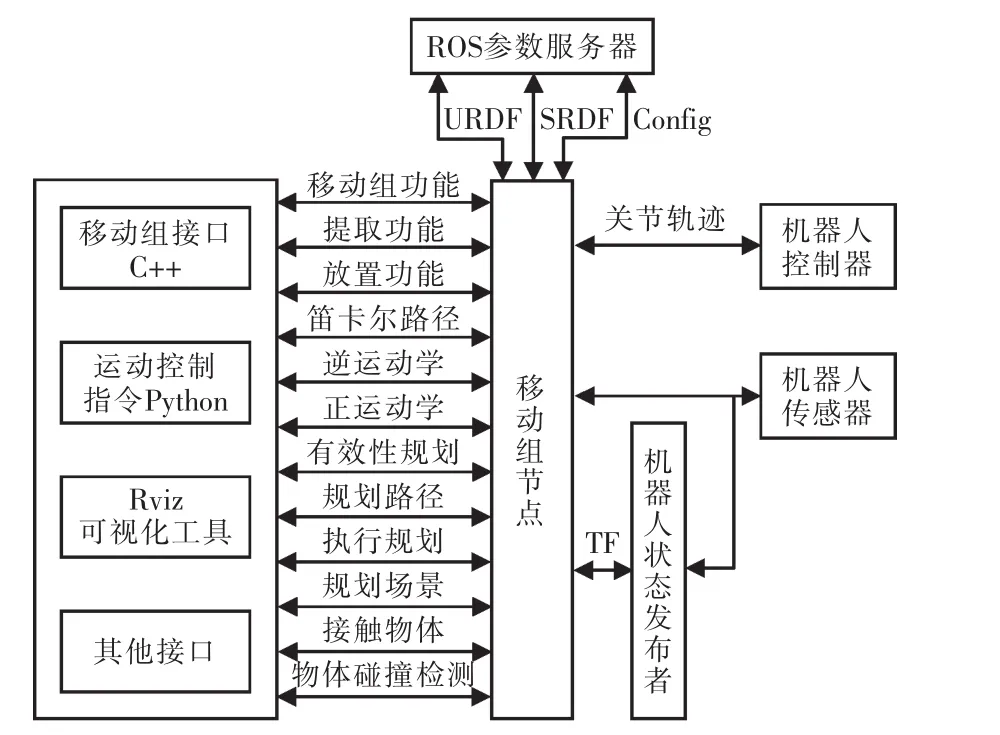
图1 MoveIt!的节点框架Fig.1 MoveIt!node framework
2 机器人模型的建立
ROS系统中利用通用机器人描述格式URDF来表示机器人模型[4]。该文件通过ROS中的robot_state_publisher节点发布机器人的坐标变换关系,以实现在任意时间,将点、向量等数据的坐标,在2个参考系中完成坐标变换,可以用于机器人轨迹规划、MoveIt!等,从而实现机器人各关节位姿的精确跟踪[5]。
对于在SolidWorks中建立的机器人模型,可以用ROS官方制作的sw2urdf插件来生成URDF文件,在ROS中使用可视化URDF工具可以生成机器人模型连杆、关节之间的关系和相应位姿的树状图,如图2所示。
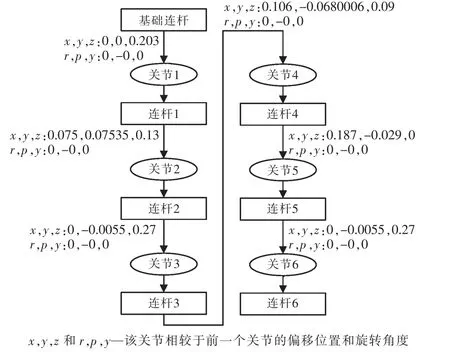
图2 机器人关节、连杆树状图Fig.2 Joint and link tree structure of robot
利用URDF文件,在ROS的工作空间中编写ROS软件包,创建节点和launch文件,在launch文件中定义启动的节点和相应的参数[6]。机器人模型在Rviz中显示如图3所示。

图3 机器人模型显示界面Fig.3 Robot model display interface
3 仿真平台设计
基于机器人操作系统所搭建的软件框架如图4所示。其中,MoveIt!为机械臂运动规划的核心工具包,主要负责运动学解算[7];OMPL为运动规划算法库,向MoveIt!提供复杂算法支持;3D可视化软件包Rviz,可直接查看机器人的结构和坐标系,进行实时仿真。
ROS平台下,MoveIt!是机械臂仿真运算的核心,Move_group节点是MoveIt!的核心节点,所有的信息都在这里汇集。通过解析URDF描述文件初始化机器人模型的运动学信息,由OMPL运动规划库生成轨迹消息包,并传递给控制器节点。控制器将数据送到ROS底层的角度轨迹控制器作为加减速控制和插补的输入;控制器在进行实时运算时,不断修改URDF模型,在Rviz中实时仿真[8]。实时运算输出的插补结果,也可以通过通讯节点输出到真实环境中的机器人上,实现实时运动。

图4 软件框架Fig.4 Sofeware framework
4 仿真实验
在所搭建的仿真实验平台上,对六自由度机械臂进行笛卡尔空间的直线和圆弧轨迹规划,以保证机器人快速平稳的运动,实现满足精度要求的轨迹。MoveIt!默认使用KDL(kinematics and dynamics library),通过数值迭代算法求解逆运动学问题。该方法对于不同机器人模型的通用性较强。
4.1 直线轨迹规划
已知机械臂末端起点 P1(xa,ya,za)和终点 P2(xb,yb,zb),并沿直线从 P1点运动到 P2点,插补的次数为N,则中间插补点的坐标(xi+1,yi+1,zi+1)为
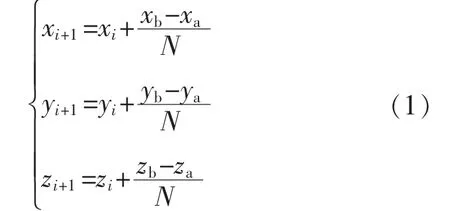
式中:i=1,2,3,…,N。
在建立的ROS仿真平台中,实现直线插补运算过程如下:先给定起点和终点,由P1运动到P2,规划的直线轨迹运动图5所示。采用笛卡尔空间的轨迹约束,通过逆解运算求得各关节的变化,并绘制关节角度变化,如图6所示。将ROS中生成的机械臂末端点位置和理论的差值位置进行比较,绘制误差曲线,如图7所示。

图5 直线轨迹运动Fig.5 Linear trajectory planning

图6 直线轨迹关节角度变化曲线Fig.6 Curve joint angle change curve of straight line

图7 直线轨迹规划误差曲线Fig.7 Error curve of linear trajectory planning
4.2 圆弧轨迹规划
在三维空间中,给定 3 个点 P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3),如图8所示。 将 P1,P2,P3这 3 点确定的唯一平面设为α,该平面方程为
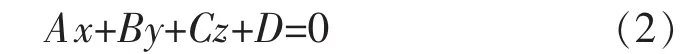
在平面α上取直线P1P2和P2P3的垂直平分线,两线相交于点 O1(x0,y0,z0),O1点即为圆弧的圆心坐标,从而可得半径R,也可求得弧P1P2和弧P2P3对应的圆心角 θ1和 θ2。
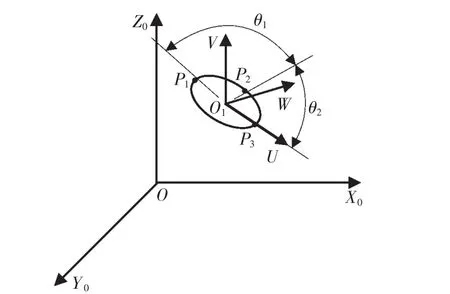
图8 笛卡尔空间的圆弧轨迹Fig.8 Arc planning in Cartesian space
由圆心坐标建立新的坐标系如图8所示,便可得到UVW坐标系相对于基坐标系的变换矩阵为

为X轴在基坐标系下的方向余弦;

为Y轴在基坐标系下的方向余弦;o=a×n为Z轴在基坐标下的方向余弦。圆弧轨迹的圆心角之和θ=θ1+θ2,插补的角度位移量为Δθ,总的插补次数为 N=,则圆弧在UV平面的插补为

式中:i=1,2,3,…,N。对于平面 UV 的任意点 P 的齐次坐标[u v 0]T,可通过式(5)将其转化到基坐标系 X0Y0Z0下,即

借助于该变换矩阵公式,对新坐标系下的圆弧轨迹点进行矩阵计算,从而可以得到在笛卡尔空间上的圆弧轨迹。在ROS平台上,实现的圆弧插补如图9所示,关节角度变化如图10所示。将ROS中生成的机械臂末端点位置和理论的差值位置进行比较,绘制的误差曲线如图11所示。
5 结语
搭建了基于ROS平台的机器人仿真平台,利用URDF文件完成了六自由度机械臂的建模,利用

图9 圆弧轨迹规划Fig.9 Circular trajectory planning
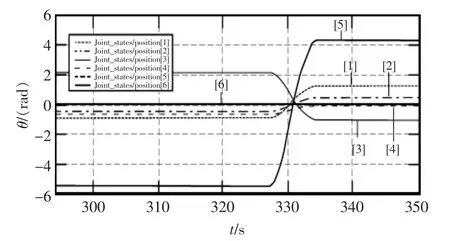
图10 圆弧轨迹关节角度变化Fig.10 Arc trajectory joint Angle change
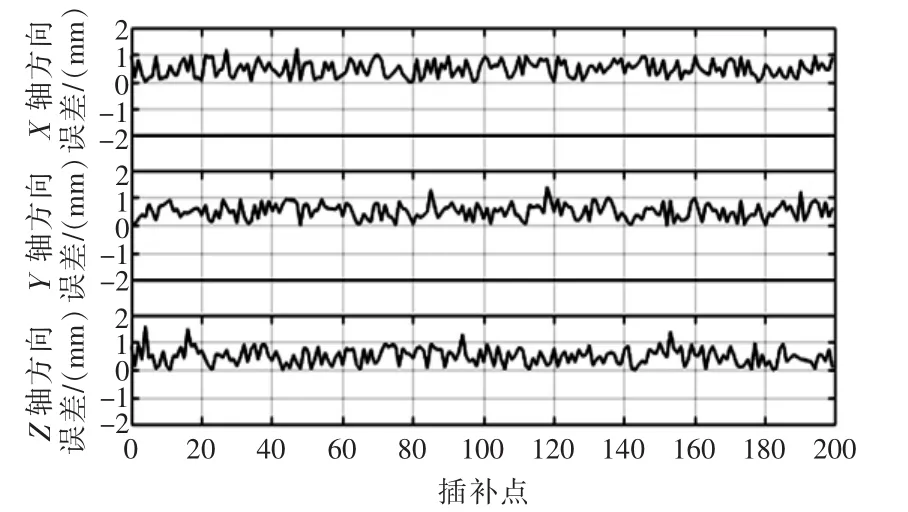
图11 圆弧轨迹规划误差曲线Fig.11 Error curve of arc trajectory planning
MoveIt!进行了六自由度机械臂的运动学解算和轨迹规划,并在Rviz上进行了三维实时仿真模拟;完成了笛卡尔空间的直线圆弧轨迹规划,实现了插补运算;在仿真平台进行了实验,通过ROS显示的各个关节的角度变化信息,可以看出六自由度机械臂各关节运动轨迹平滑,轨迹误差满足要求,验证了该方法的有效性。
参考文献:
[1]陈盛龙,平雪良,曹正万,等.基于ROS串联机器人虚拟运动控制及仿真研究[J].组合机床与自动化加工技术,2015,52(10):108-111.
[2]曹正万,平雪良,陈盛龙,等.基于ROS的机器人模型构建方法研究[J].组合机床与自动化加工技术,2015,52(8):51-54.
[3]徐扣.六自由度机械臂的逆运动学求解与轨迹规划研究 [D].广州:广东工业大学,2016.
[4]Hoske M T.ROS Industrial aims to open unify advanced robotic programming[J].Control Engineering,2013,60(2):20-21.
[5]郑梓均.基于ROS系统的简易服务机器人关键技术的研究[D].无锡:江南大学,2016.
[6]JOSEPH L.Mastering ROS for robotics rrogramming[M].Birmingham:Packet Publishing Ltd,2015.
[7]Chitta S,Sucan I,Cousins S.“Moveit![ROS topics]”[J].Robotics&Automation Magazine IEEE,2012(19):18-19.
[8]左轩尘,韩亮亮,庄杰,等.基于ROS的空间机器人人机交互系统设计[J].计算机工程与设计,2015,36(12):3370-3374.

