对一道高考压轴题的评析
黄如炎
福建省闽清县教师进修学校 (350800)
题目已知函数f(x)=ae2x+(a-2)ex-x.
(1)讨论f(x)的单调性.
(2)若f(x)有两个零点,求a的取值范围.
(2017年高考全国(I)卷理科压轴题)
1.试题赏析
本题以函数零点为载体考查导数与函数单调性等知识,考查推理论证能力、运算求解能力、创新意识,考查函数与方程思想、化归与转化思想、分类与整合思想、有限与无限思想、数形结合思想,是考查学生数学关键能力、学科素养和核心价值的把关试题.不可求的函数零点问题,是高考的热点与难点,学生解题思路茫然.高考命题组给出的参考解答具有严谨、精炼、规范的特点,体现了数学的理性思维,颇有数学味.但由于没有给出零点探求的思维过程(连图形都没有),使师生很难领悟命题组的参考解答,对直接给出的结论,学生感到突如其来,百思不得其解[1].
2.解题分析
“数学是自然的,数学是清楚的”[2],因此数学解题应是清析明理的.解决不可求函数零点问题要顺应学生形象思维到抽象思维的认知过程,通过求导作图,特值验证,放缩化归等有效手段,引导学生经历数学发现、数学创造的思维历程,揭示蕴含在知识背后的核心素养、数学本质和思想方法,让解题思维从学生头脑里自然地流淌出来.以下给出该压轴题的几种原创自然解法,供同行教学参考.
解析1:(1)f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1).
①若a≤0,则f′(x)<0,f(x)在(—∞,+∞)单调递减;
②若a>0,当x∈(-∞,-lna)时,f′(x)<0,当x∈(-lna,+∞)时,f′(x)>0,所以f(x)在(-∞,-lna)单调递减,在(-lna,+∞)单调递增.
(2)①若a≤0,由(1)知,f(x)至多有一个零点;

图1
②若a>0,由(1)知

还可用以下解析2、解析3探求n.
解析2:(1)同解析1.


综上:a∈(0,1)时,f(x)有两个零点.
解析3:(1)同解析1.

综上:a∈(0,1)时,f(x)有两个零点.
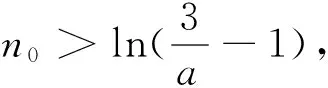

图2
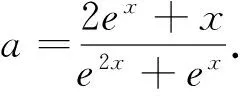
故a∈(0,1)时,f(x)有两个零点.
3.归纳总结
探求连续函数f(x)不可求零点的存在区间,可运用以下有效方法:
(1)求导,确定函数f(x)的单调区间;
(2)作图,作出函数f(x)图像判断零点的情况;
(3)探值,在零点两侧分别探求实数m、n(可以是一个具体的数式或区间),使f(n)f(m)<0.
①特值验证:根据函数式的特征,取特殊自变量m,验证是否满足f(m)>0(或f(m)<0).
②解不等式:当不等式f(x)>0(或f(x)<0)可解时,可直接通过解不等式求出满足f(m)>0(或f(m)<0)的实数m.
③放缩化归:当f(x)较复杂时,可将f(x)放缩为简单的函数g(x),使f(x)>g(x)(或f(x) 由于零点问题基本以指数函数、对数函数、三角函数等基本初等函数为载体,为熟练放缩,要求学生掌握重要不等式ex≥x+1,lnx≤x-1,sinx≥0(x≥0). 图3 (原创题)已知f(x)=(x-1)ex-kx2+2,当x∈[1,2]时,f(x)<0,探求f(x)的零点个数. 解析1:f′(x)=x(ex-2k),由f(1)<0,得k>2,∴ln2k>1,所以f(x)在(-∞,0)和(ln2k,+∞)单调递增,在(0,ln2k)单调递减.易取x=0,x=1,得f(0)=1>0,f(1)=2-k<0.当x→-∞时,f(x)→-∞,当x→+∞时,f(x)→+∞,知f(x)图像如图3所示且有三个零点.f(-1)=-2e-1-k+2<0,f(ln2k) 由于ln2k=ln2+lnk≤ln2+k-1 解析2:当x>ln2k时,因为ex>x2,x>ln2k>1,所以f(x)=(x-1)ex-kx2+2>(x-1)x2-kx2+2=(x-1-k)x2+2,令g(x)=(x-1-k)x2+2,为消去x项,取x=1+k,则g(k+1)=2>0,所以f(k+1)>0,故f(x)在(ln2k,k+1)上有一个零点. 评注:本例的难度在于寻找一个大于ln2k的数使其函数值大于零.解决的智慧一是利用重要不等式lnx≤x-1找到大于ln2k的数k,二是把f(x)放缩为简单的函数g(x)=(x-1-k)x2+2,再取特值x=1+k,使f(k+1)>g(k+1)>0. [1]教育部考试中心.2017年普通高等学校招生全国统一考试试题、参考答案[M].福州:福建省教育考试院,2017. [2]刘绍学.普通高中课程标准实验教科书﹒数学1-5必修[M].北京:人民教育出版社,2007.
4.变式引申

