卫星载荷磁场优化计算方法研究

李 恪，姚崇斌，徐红新，谢宝蓉

(上海航天电子技术研究所，上海 201109)

0 引言

地磁测量是卫星弱磁探测技术的重要应用之一，对整个地球的磁场环境描述有着重要的意义[1-4]。因卫星与地球相距非常远，故卫星所处空间的地磁感应强度很小。但卫星在轨工作时，整星内部会形成一个基本稳定的磁场。卫星内部磁场与地磁场相互作用形成磁场干扰力矩，严重影响姿态控制及地磁测量的精度。为减少星上磁场噪声的影响，需要在地面上测量载荷的磁场，并做消磁处理。

现有的磁场测量方法大多采用数值计算方法，将被测物体划分为许多小的磁场单元，对各个单元在不同方向上的磁场分量进行积分，从而得到被测物体总的磁场，如有限元法、积分方程法等。有限元法要求在整个求解区域内进行离散剖分，计算数据的前处理较繁杂，且计算开域问题时需要截断边界，故有限元法的使用范围受限。积分方程法中系数矩阵元素的计算为三重体积分，计算较复杂，且当源点和场点重合时，系数矩阵的计算带有奇异积分。该方法的优点是剖分简单，待求解未知量少，但非对称满阵导致占用资源大，计算时间长。

地磁场是一个弱磁场，对于处于不同地磁场中的载荷，可认为其磁化率基本不变。故针对数值计算方法的不足，根据实际应用的需求，采用三维静磁场逆计算方法的思路[5-7]，对传统的数值计算方法加以优化。

本算法利用某处地磁场下卫星载荷的磁场测量数据，逆计算卫星载荷的等效磁化率，根据等效磁化率计算卫星载荷产生的感应磁场，根据均匀磁化卫星载荷的特点，将积分方程法中系数矩阵元素的体积分形式化为面积分形式，并消除积分计算的奇异性，建立基于单元表面积分的感应磁场计算模型。最后，以实际载荷为实验对象，验证算法的有效性。相比传统算法，在保证精度的前提下，极大地提高了工作效率。

1 基于表面积分的均匀磁化体磁场计算模型

基于体积分的积分方程法磁场计算公式为[2]

Hm(r)=

(1)

式中：Hm为铁磁物体产生的磁场；M为铁磁物体内部磁化强度；r为场点的坐标；r′为源点的坐标；V为铁磁物体的体积。由式(1)计算铁磁物体的磁场时需要计算三重积分，计算较复杂，且当场点和源点重合时，积分计算具有奇异性。

在不存在自由电流的区域中，从磁荷观点出发，均匀磁化卫星载荷产生的标量磁位[8]可表示为

(2)

(3)

式中：dS为单位面元的投影面积；n为曲面S在r处的法向矢量。故均匀磁化卫星载荷在空间产生的磁场强度可表示为

(4)

一般情况下，不规则卫星载荷在外磁场中未被均匀磁化。若将卫星载荷剖分成N个小单元，当剖分单元体积足够小时，则可认为每个小单元是等效均匀磁化体。由磁场叠加原理可知，卫星载荷在空间产生的磁场强度为所有等效均匀磁化体的叠加，即式(4)可表示为

(5)

考虑到每个剖分单元卫星载荷的线性度和均匀性，设每个剖分单元满足Mi=χiHi， 式(5)可进一步表示为

(6)

式中:χ=[χ1,χ2,…,χN]为待优化的参数组。一般情况下，该问题很难直接求解，但通过迭代过程，即多次计算不同的χ所对应的目标函数值，即可逼近问题的真实解。当已知每个剖分单元的磁化率和磁场强度时，根据式(6)就可计算出卫星载荷在空间任一点产生的感应磁场。

假设卫星载荷处于外磁场为He的空间，则空间任一点的磁场H=He+Hm。当把场点配置在第j个剖分单元的中心时，可得到第j个剖分单元中心磁场强度的表达式为

(7)

写成矩阵形式为AH=He，其中系数矩阵A由场点坐标、剖分单元中心坐标及单元磁化率决定，H为每个剖分单元中心的磁场强度。

已知卫星载荷的磁性参数，根据式(7)建立每个单元中心处磁场强度的线性方程组，求解该方程组即可得到每个剖分单元的磁场强度，再由式(6)就可计算卫星载荷在空间任一点产生的感应磁场。由此可看出，系数矩阵元素的计算为面积分的形式，较传统的体积分形式简单；由于积分是在剖分单元表面进行，而场点选取在剖分单元的中心，故当源点和场点重合时，积分计算无奇异性。

2 基于微粒群算法的等效磁化率逆计算方法

2.1 微粒群算法的基本原理

微粒群算法中，所有粒子都有一个由被优化函数决定的适应值，每个粒子还有一个速度用于决定他们搜索的方向和距离，粒子们追随当前的最优粒子在解空间中搜索。在求解过程中，微粒群初始化为一群随机粒子(随机解)，并通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自身，第一个极值是粒子本身所找到的最优解，即个体极值；另一个极值是整个种群目前找到的最优解，即全局极值。找到这两个最优值后,粒子根据如下的公式来更新自己的速度和新的位置[9]

(8)

式中：vi为粒子的速度；xi为当前粒子的位置；pbest为个体极值；gbest为全局极值；xrand为介于0与1之间的随机数；c1、c2为学习因子；w为惯性权重；t为迭代的次数。每一维粒子的速度都会受限于最大速度vmax，如果粒子某一维更新后的速度超过vmax，那么这一维的速度就被限定为vmax。

2.2 计算方法与流程

由于外加磁场的影响，卫星载荷的磁性状态会根据外磁场的大小，沿着其磁化曲线工作于相应的磁化点。电磁场逆问题是由果求因的问题[10]，在静磁场计算中即为已知磁场测量数据来反演卫星载荷的磁性参数。建立的逆问题数学模型可表示为

(9)

由式(9)可知，模型中有N个未知数，故将粒子的解空间设置成N维空间，每个粒子的坐标为[χ1,χ2,…,χN]，粒子的适应度函数取为式(9)中的J，每个粒子具有的速度v=[v1,v2,…,vN]，第t+1代粒子在第t代粒子的基础上按式(8)更新自己的位置和速度，其优化过程如下：

1) 设置相关初始参数，如粒子群规模m、惯性权重w、学习因子c1和c2、粒子最大飞行速度vmax、迭代结束条件；

2) 初始化粒子的位置及速度；

3) 评价各粒子的适应度函数；

4) 对每个微粒，将其适应度值与历史最好位置pbest相比较，若当前适应度值更优，则用当前适应度值更新pbest；

5) 将每个微粒的适应度值与群体经历过的历史最佳位置gbest相比较，若当前群体中最好的适应度值较好,则将其设置为新的gbest；

6) 根据式(8)更新各微粒的位置和速度；

7) 计算优化目标函数，若达到精度要求或迭代次数，则返回当前最佳微粒的结果，算法结束，否则返回步骤3)。

3 实验方案与结果分析

3.1 实验方案

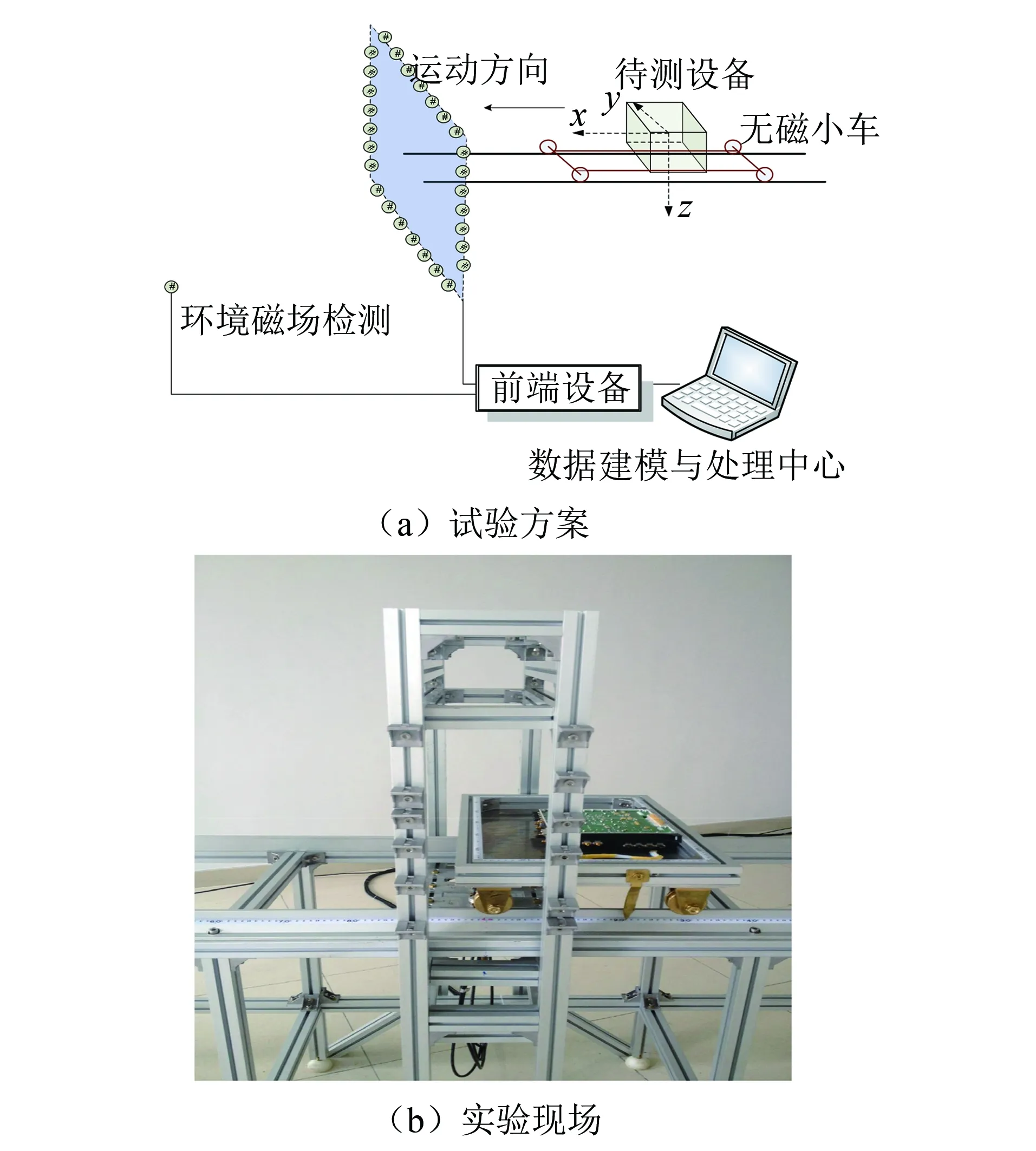
图1 实验方案及现场示意图Fig.1 Schematic diagrams of experimental scheme and experimental site

为考察不同场点、不同外磁场及不同磁化方向下计算的感应磁场的准确性，测量时，被测物体先沿南北方向滑动测量，再转动测量架，使被测物体沿东西方向滑动测量。地磁平面的选取标准原则上是离被测物体越近越好，但是要考虑到其他设备的干扰，因此需要综合考虑取测量偏差较小的距离。用上述相同的方法测量纵向载荷上端高度为h2、载荷下端高度为h3，以及横向载荷下端高度为h4时的平面磁场数据，以用于与计算值比较。

3.2 实例计算过程说明

应用本文算法计算卫星载荷感应磁场过程中，兼顾计算时间和计算精度，将载荷剖分为20×5个长方体单元，并假定每个剖分单元为等效均匀磁化体。应用微粒群优化算法反演计算磁化率的过程中，考虑到载荷材料的均匀性，认为每个剖分单元在地磁场的作用下的磁化率相同，故式(8)可简化为只含一个未知数的优化问题，相应的粒子的解空间为1维空间，即待优化的参变量χ=[χ,χ,…,χ]。

用微粒群优化算法进行优化求解时，参数设定为：微粒粒子数m=40，惯性权重w=0.9，学习因子c1=c2=2，最大速度vmax=10，迭代次数50。为考察微粒群算法反演磁化率的有效性， 逆计算15次。图2为15次逆计算所得的等效磁化率和最终最优粒子的适应度曲线和一次逆计算时粒子适应度的收敛曲线。由图2可知，用微粒群优化算法反演磁化率是有效的，且收敛速度较快。计算卫星载荷感应磁场时所用磁化率取15次逆计算得到的等效磁化率的平均值为140.8。图3为卫星载荷受地磁场水平分量纵向磁化和横向磁化时，产生的感应磁场三分量测量值和计算值对比曲线。由图3可看出，测量值和计算值吻合较好，其最大相对误差约为10.79%。

图2 磁化率逆计算参数图和收敛曲线Fig.2 Parameters and convergence curve of magnetic susceptibility inverse calculation

4 结束语

由均匀磁化体的磁化特点出发，建立了基于单元表面积分的卫星载荷感应磁场求解方法。与传统基于体积分的磁场求解方法相比，该方法简化了系数矩阵运算，消除了源点和场点重合时的积分奇异性。以卫星载荷的磁化率为未知量，建立了求解磁化率的数学模型，并运用随机类微粒群优化算法对其求解。最后，以卫星载荷为计算实例，验证了本文算法的可行性，计算值与测量值具有较好的一致性。结果表明，该方法完全可用于卫星载荷感应磁场的计算。

图3 不同磁化方向、不同场点的感应磁场Fig.3 Induction magnetic field at different magnetization directions and field points

[1] 吴卫权. 地磁场中卫星不侧置态下磁矩测试方法[J]. 上海航天, 2014, 31(1): 50-55.

[2] 徐文耀. 地磁场的三维巡测和综合建模[J]. 地球物理学进展, 2007, 22(4): 1035-1039.

[3] 傅绥燕， 宗秋刚, 濮祖荫. 地磁活动与太阳活动对环电流离子成分与位置的影响[J]. 地球物理学报, 2003, 46(6): 725-730.

[4] 林瑞淋, 张效信, 刘四清. 高纬磁层顶位形统计分析[J]. 地球物理学报, 2003, 53(1): 1-9.

[5] PECHENKOV A N . A mathematical algorithm for solving the inverse problem of magnetostatic flaw detection[J]. Russian Journal of Nondestructive Testing, 2005, 41(11): 714-718.

[6] PECHENKOV A N. Numerical simulation of an inverse problem of magnetostatic flaw detection[J]. Russian Journal of Nondestructive Testing, 2005, 41(11): 719-723.

[7] 周克定. 工程电磁场专论[M]. 武汉: 华中工学院出版社, 1986: 28-29.

[8] 樊明武, 颜威利. 电磁场积分方程法[M]. 北京: 机械工业出版社, 1988: 65-68.

[9] 连丽婷, 杨明明, 孙开江. 基于改进微粒群算法的磁靶电流参数优化调整[J]. 舰船科学技术, 2015, 37(3): 73-76.

[10] 黄卡玛, 赵翔. 电磁场中的逆问题及应用[M]. 北京: 科学出版社, 2005: 13-19.