热压混合材料板力学特性PSO-SVR模型预测
周修理,王 飞,刘明玮,王德福
(1.东北农业大学电气与信息学院,哈尔滨 150030;2.东北农业大学工程学院,哈尔滨 150030)
混合材料板以木材和农作物秸秆为原料,经热压形成高分子材料,应用广泛。我国混合材料板制造行业存在能源消耗高、环境污染、产品质量低等问题。因此,高效利用木材和农作物秸秆,缓解木材资源供需不平衡,提高自然资源利用率、增加附加值、改善环境、实现自然资源可持续利用尤为重要。基于森林资源和混合材料板供需矛盾,建立精确、快速混合材料板热压控制预测模型具有实用价值[1-2]。
热压过程检测和控制方面,Steve等开发人造板热压监测系统用于检测热压过程板坯温度、压力、厚度和含水率等工艺参数[3]。陈天全自主研发热压温度、热压压力和原料含水率实时检测系统,实时检测温度、压力、含水率等参数并发现其变化规律[4]。王东林等基于PROFIBUS现场总线技术,构建分布式智能控制系统,运用模糊调节算法及模糊规则调节算法主要参数,实现热压过程优化控制[5]。王宁等分析热压生产过程,建立双模控制器,应用改进粒子群算法优化控制器参数,提高控制系统鲁棒性和精度[6]。
热压过程建模和性能预测方面,Harless等分析板坯垂直密度分布与板芯温度和热压压力分布,构建数学模型[7]。Humphrey等研究分析热压过程原料含水率、热压温度、热压压力等因素,运用有限差分方法构建热压过程温度、压力、含水率预测模型[8]。Zombori等开发热压过程二维模型考虑空气、水蒸气、结合水含量、板坯芯层温度和固化指数,利用微分-代数系统求解器求解[9]。该数学模型可预测并优化热压过程温度、含湿量、局部空气和蒸汽压力、总压力、相对湿度及粘合剂固化指数等参数。谢力生等认为板芯层温度影响因素有热压温度、原料含水率、板材厚度等,确定温度变化与板材性能参数间关系[10]。刘亚秋等研究热压过程板间距离、热压压力、热压温度、压机闭合速度、热压时间等因素得到最佳生产工艺方案[11]。田燕青通过分析热压过程与BP神经网络特点,将该算法应用于中密度纤维板热压参数优化和预测,利用试验样本集合训练、学习建立基于BP神经网络热压过程预测模型,预测不同热压生产工艺条件下中密度纤维板性能,提高产品质量和生产效率[12]。盖玲等利用BP神经网络建立热压工艺参数与板材力学特性间预测模型,该预测模型可预测混合材料板力学性能指标[13]。孙建飞等通过多因素均匀试验研究热压工艺参数对稻壳和木材复合材料弹性模量和静曲强度影响[14]。符彬等以甘蔗渣纤维为原料,采用热压技术制备无粘结剂蔗渣纤维板,研究无粘结剂甘蔗渣纤维板密度、热压温度和热压时间对无粘结剂蔗渣纤维板物理力学性能影响[15]。Tiryaki等建立人工神经网络和多元线性回归模型,根据热压温度、热压时间、热压压力及胶粘剂类型预测刨花板静曲强度和弹性模量[16]。潘亚鸽等以麦秸、木材和环保型阻燃无机胶粘剂为主要原料,采用热压技术制备麦草与木材均匀混合无机刨花板,通过研究麦草木比、胶粘剂用量、热压过程X射线衍射并以扫描电子显微镜分析热压时间和热压温度对板材物理静曲强度、弹性模量、内部结合强度及吸水厚度膨胀率影响作用,确定最佳热压工艺[17]。彭顺等研究大豆基粘合剂粘接竹纤维刨花板静曲强度、弹性模量、内部结合强度及吸水厚度膨胀率,探讨热压温度、热压时间、粘合剂用量和防水试剂含量对大豆基粘结竹刨花板性能影响[18]。孙建平等利用遗传算法和神经网络预测力学性能[19-20],该网络模型非线性映射能力更强、稳定性更高,但预测易陷入局部极小值。于海英针对中密度纤维板热压小样本问题、训练样本不足问题,提出采用支持向量机建模方法构建热压工艺参数与板材力学性能指标关系模型,并用网格搜索法优化参数[21],预测混合材料板力学特性,但易陷入局部最优。
针对上述问题,本文结合支持向量机理论(Support Vector Machine,SVM)和粒子群优化算法(Particle Swarm Optimization,PSO),通过正交试验设计并结合混合材料板力学特性测试样本数据,以热压压力、热压温度、含水率、热压时间为自变量,选取静曲强度、弹性模量、抗拉强度为因变量,构建热压工艺参数与混合材料板力学特性间非线性预测模型,提出将PSO嵌入SVR算法,选择和优化热压控制参数,以期获得全局最优混合材料板力学特性预测模型。研究结果可为混合材料板静曲强度、弹性模量、抗拉强度预测及热压控制参数选择提供参考依据。
1 热压过程分析与热压试验设计
1.1 热压过程分析
热压是混合材料板生产主要工序之一,对板材力学特性起决定作用。混合材料板密度、厚度和力学特性与热压控制参数密切相关[22]。热压过程主要原理是热压机根据工艺要求向蓬松板坯提供热量并施压,热量与压力共同作用促使板坯中水分汽化、蒸发,各种成分发生系列理化变化。胶粘剂固化,防水剂重新分布,促进板坯纤维紧密接触与交织,形成多种结合力,生产符合特定要求混合材料板。其过程可分为压缩、温度渗透、厚度控制和卸压4个阶段。热压过程是复杂非线性系统,主要参数包括两个方面:一是原料参数,包括原料类型、胶粘剂种类、含水率等,该参数对混合材料板密度及密度分布均匀性和可塑性具有重要影响;二是热压控制参数,包括热压压力、热压温度、热压时间等,在该参数耦合作用下形成具有特定力学特性混合材料板。混合材料板力学性能指标主要包括静曲强度、弹性模量、内结合强度等。其中,静曲强度是混合材料板承受压力直到断裂最大压力强度;弹性模量反映混合材料板弹性形变程度;内结合强度反映混合材料板内部纤维胶合质量。实际混合材料板生产过程中热压压力、热压温度、热压时间及原料含水率等因素相互作用、相互影响,需协同控制以满足工艺需求。
1.2 热压试验设计
1.2.1 试验仪器及材料
以热压控制过程为研究对象,实验仪器、材料为:100 t试验热压机、50 t试验热压机、空气压缩机、纤维拌胶机、SC69-02型水分快速测定仪、台秤、天平、计时表、烧杯、量筒、玻璃棒、干燥杂木纤维、脲醛树脂胶、固化剂、防水剂等。试验材料、指标及热压控制参数范围如下:木纤维初始含水率30%~40%,采用脲醛树脂胶粘剂,固体胶含量为50%,成品板目标厚度12 mm,密度0.80~0.85 g·cm-3,铺装线含水率约10%,全程热压时间约180 s,热压温度约170℃,热压过程时间约3 min。
1.2.2 热压试验流程
(1)原料用量计算:用SC69-02型水分快速测定仪测定纤维含水率,确定混合材料板密度、施胶量、胶粘剂和固化剂用量、防水剂用量;根据混合材料板幅面尺寸及厚度计算绝干纤维重量,确定绝干纤维重量和纤维含水率及实际需要湿纤维重量;根据计算干胶量,按液体胶固体含量计算需要液体胶含量;根据预定固化剂用量比例计算实际用量;根据预定防水剂用量比计算实际用量。
(2)拌胶:将纤维原料倒入拌胶机内,胶粘剂和固化剂混合,其间不断搅拌,以防局部快速固化,倒入喷枪杯。防水剂可与胶粘剂合喷,也可单喷;待纤维、胶粘剂、防水剂准备完毕,开动搅拌机和空气压缩机拌胶。控制好拌胶机转速和搅拌时间以保证纤维和胶粘剂充分混合。空气压缩机压力一般控制在0.4~0.5 Mpa;拌胶后纤维刨花含水率在13%以下,即可保证混合材料板质量,防止鼓泡和分层现象,缩短热压时间,提高效率。
(3)铺装:垫板使用前,为防止热压后粘板,可在混合材料板板坯与垫板接触处涂擦少量油酸,放入模框箱下面;将拌胶纤维手工铺装,为使纤维分布均匀,防止由于铺装不均热压造成混合材料板密度不均,在模框箱铺装口上放置金属丝网,使纤维通过属丝网而均匀地落入模框箱内。
(4)预压:拌胶纤维在模框箱内铺装完毕,送入预压机。预压机内预压15~20 s,单位压力一般为1.5~1.8 Mpa;预压成型后,板坯从预压机卸下,拆掉模箱,为防止热压后粘板,在板坯下面放置垫板。
(5)热压:根据要求混合材料板厚度,选取厚度规放在热压板上;将预压后板坯同上下垫板一同放入热压机中。12 mm厚混合材料板热压条件:温度约170℃,时间约3 min,压力约15~18 Mpa;热压后,降压卸板。使压机缓慢或分段降压,以免过快发生鼓泡。
(6)力学特性测定:混合材料板弹性模量、静曲强度及内结合强度性能指标测定参照《人造板及饰面人造板理化性能试验方法》国家标准(GB/T11657-1999)。
1.2.3 试验方法
影响混合材料板静曲强度、弹性模量、内结合强度主要因素包括热压压力、热压温度、热压时间与含水率。结合试验热压机工作参数,通过理论分析及预实验确定因素取值范围,综合考虑热压工艺要求,选取热压压力为16~17 Mpa,热压温度为168~172℃,热压时间为120~130 s,纤维含水率9.5%~10.5%。以混合材料板静曲强度、弹性模量、内结合强度为评价指标。正交试验因素水平如表1所示。

表1 正交试验因素水平Table1 Factorsand levelsof orthogonal test
2 预测模型算法原理
2.1 支持向量机原理
支持向量机是基于小样本统计学习理论和结构风险最小化原则建模方法[23]。将支持向量机解决回归预测问题即支持向量机回归(Support Vector Regression,SVR)[24]。
假设 n 个训练样本集合(xi,yi),xi∈ Rn,yi∈R,i=1,2,…,n。xi表示输入值,yi表示输出值,根据样本集合寻找最优函数f(x)=〈w,x〉+b。其中〈w,x〉表示w和x内积,〈w,x〉=wTx。表示预测模型混合材料板板材属性与热压控制参数系数组成向量。考虑现实误差,引入不敏感损失参数ε、松弛变量ζi、ζi*和惩罚因子C。优化方程为:
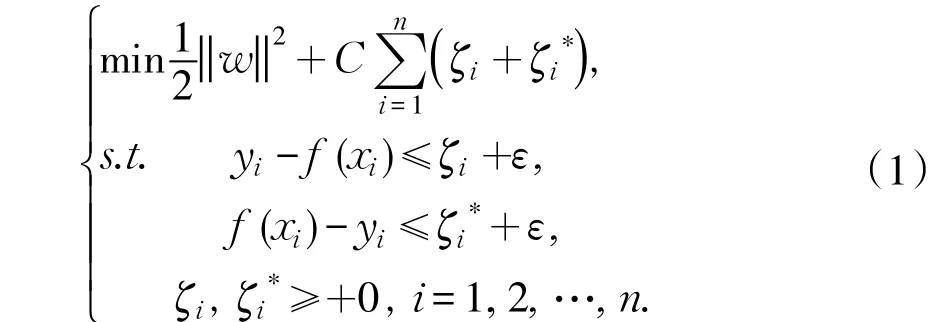
由函数极值条件求解Lagrange乘子式,得对偶问题。其中α,β,为拉格朗日乘子。
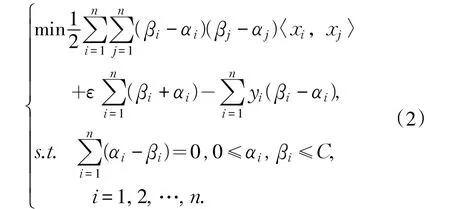
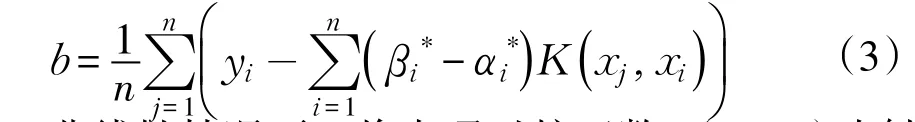
非线性情况下,将点通过核函数K(xi,xj)映射到高维空间。得到非线性回归函数

支持向量机核函数通常有以下三种:多项式Polynomial核函数、RBF核函数以及Sigmoid核函数。相比其他核函数,RBF核函数具有性态良好、参数少等优点[26],故选用RBF核函数为试验核函数构建预测模型。其参数初值范围设置:
RBF核函数:exp(-gamma*|u-v|2)C∈[0.01,1000],gamma∈[0.001,10]
为研究板坯属性、热压控制参数及混合材料板力学特性三者之间非线性关系,本文利用支持向量机非线性建模理论构建以热压工艺参数和板坯属性为自变量,以混合材料板性能指标为因变量关系模型。基于SVR原理热压控制模型结构图如图1所示。
本文采用5倍交叉验证方法优选参数,即将训练样本集合分为5个子集合且两两互不相交,其中4个子集合作为训练集,训练数据建立回归预测模型;剩余一个子集作为测试集,验证模型性能。根据图1,分别对以下三种情况建立预测模型。
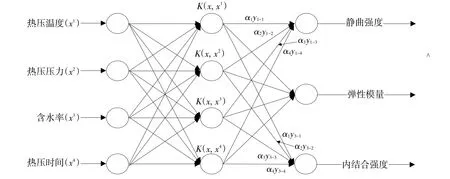
图1 基于SVR原理建立热压控制模型结构图Fig.1 Structuredigram of hot-pressing technology processbased on SVR
模型一:以热压温度、热压压力、热压时间、含水率为自变量,以静曲强度为因变量;
模型二:以热压温度、热压压力、热压时间、含水率为自变量,以弹性模量为因变量;
模型三:以热压温度、热压压力、热压时间、含水率为自变量,以内结合强度为因变量。
2.2 PSO算法参数寻优
由于SVR预测模型性能主要受惩罚因子C与RBF核函数参数g影响[27],模型参数选取直接影响预测模型拟合精度和稳定性。为提高混合材料板力学特性预测精度,选择算法优化支持向量机回归模型中惩罚因子C和RBF核函数参数g尤为重要。为避免网格搜索法优选参数易陷入局部最优,本文将粒子群算法嵌入SVR算法,对SVR参数选择和优化。粒子群算法具有计算速度快、全局搜索能力强等优点[28]。
其基本思想:在D维目标搜索空间,有m个粒子由3个向量表示,第i个粒子当前位置可表示为xi=(xi1,xi2,…,xiD)T,速度为 vi=(vi1,vi2,…,viD)T;pi=(pi1,pi2,…,piD)T表示第 i个粒子个体极值点位置;pg=(pg1,pg2,…,pgD)T表示整个种群全局极值点位置[29]。粒子根据个体极值点和全局极值点重新确定本身位置和速度,速度和位置更新如式(5):
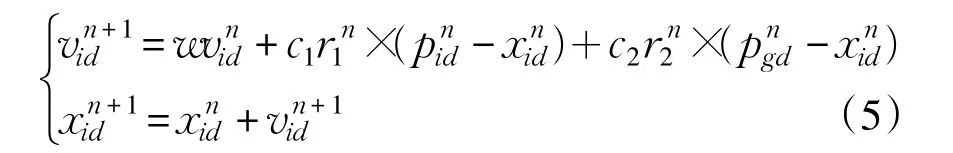
其中,位置更新公式由三部分组成:量部分、个体认知部分及社会认知。为第n次迭代粒子i位置矢量第d维分量;为第n次迭代粒子i位置矢量第d维分量;pid为粒子i个体最好位置pbest第d维分量;pgd为群体最好位置gbest第d维分量;w表示惯性权重;c1和c2为学习因子;和为[0,1]区间随机数。PSO算法实现步骤:
(1)初始化粒子群,即初始化种群数量、初始搜索点位置及速度,并设定初始参数;
(2)确定适应度函数并计算适应度值;
(3)根据式(4)更新粒子位置和速度,包括更新每个粒子状态、种群中个体最优位置及全局最优位置;
(4)判断是否满足终止条件。若满足条件,则终止迭代,输出全局最优解;否则跳转至步骤(2)。
基于上述分析,应用PSO算法对热压混合材料板SVR预测模型参数优化,具体实现流程如图2所示。
2.3 预测模型评价标准
为更好评价预测模型精度,以均方误差和拟合优度为预测模型评价指标[30]。其中,均方误差反映预测模型实际值与预测值误差,越小说明预测精度越高。拟合优度越接近1,说明回归函数对数据拟合效果越好,即自变量对因变量解释程度越好。为避免输出各性能参数差别较大对模型计算造成影响,分别对混合材料板静曲强度、弹性模量和内结合强度作最大-最小标准归一化处理。
3 结果与分析
3.1 试验结果
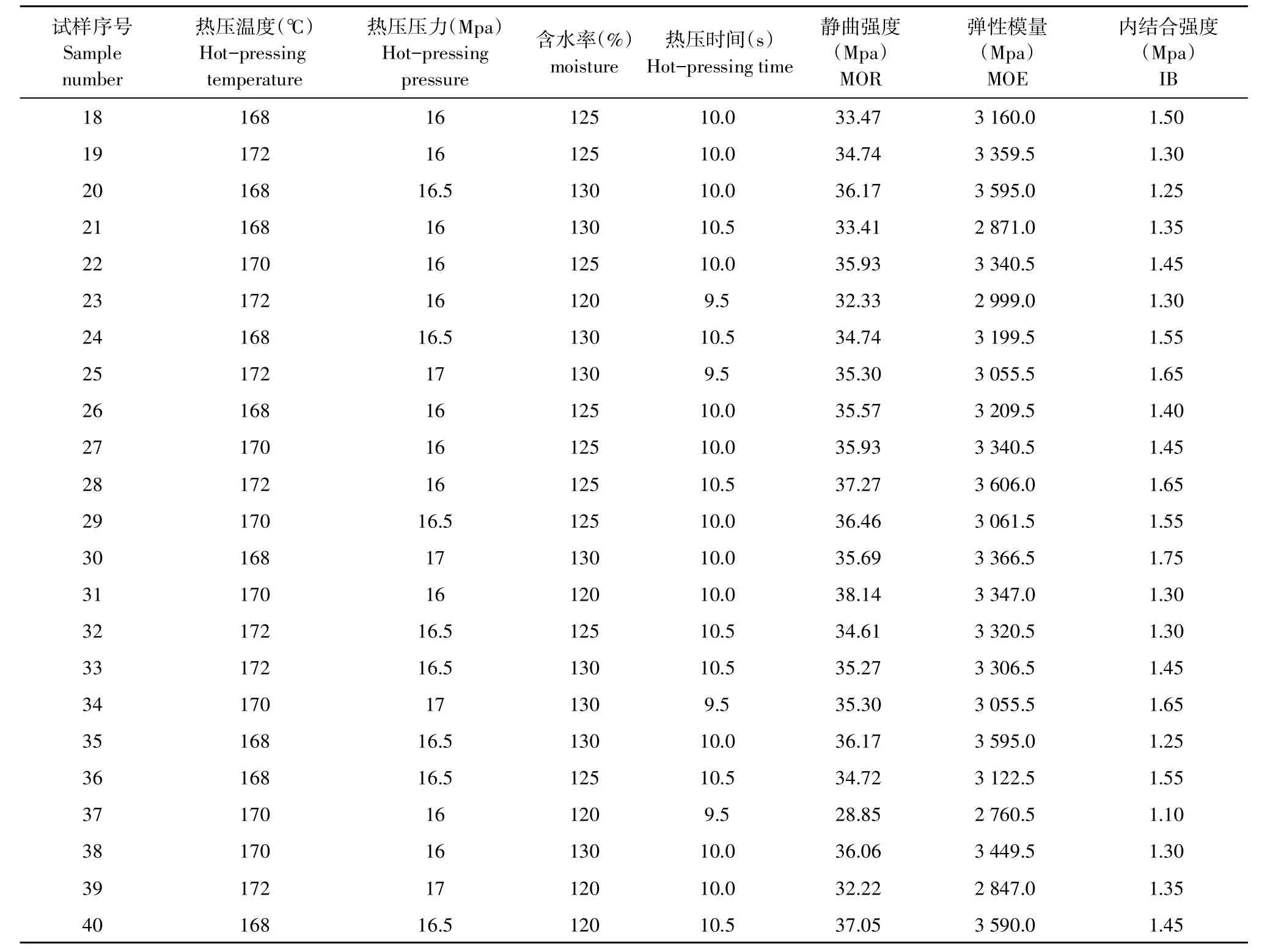
为降低测试试验造成随机误差,在相同条件下,分别测量试验样本组静曲强度、弹性模量和内结合强度,取5次测量值算术平均值作为测试结果。训练和测试基于正交试验性能测试小样本数据,其中前10组为测试集样本数据,后30组为训练集样本数据,试验数据如表2所示。
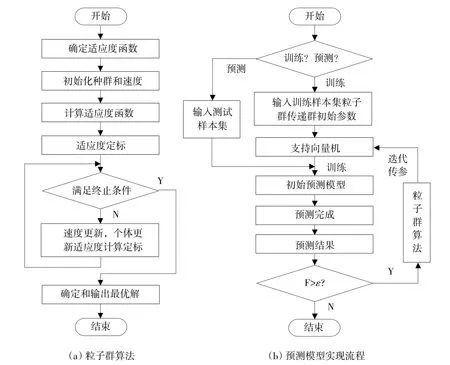
图2 粒子群算法及预测模型实现流程Fig.2 Particleswarm optimization and implementing flow of predictivemodel

表2 试验数据Table2 Experimental data
续表
3.2 PSO-SVR算法参数设计
PSO-SVR算法设计主要包括设定种群初始参数和构造适应度函数,本文适应度函数曲线反映PSO-SVR算法优化前后均方误差变化。PSO-SVR算法参数设定如表3所示[31]。
正交试验数据如表2所示,随机选取试验数据75%作为训练集用建立预测模型,剩余25%作为测试集验证预测模型性能。混合材料板静曲强度、弹性模量、内结合强度归一化测试集预测值与实际值拟合结果分别如图3(a)、(b)、(c)所示。可见混合材料板静曲强度、弹性模量、内结合强度测试集预测值与实际值误差较小。
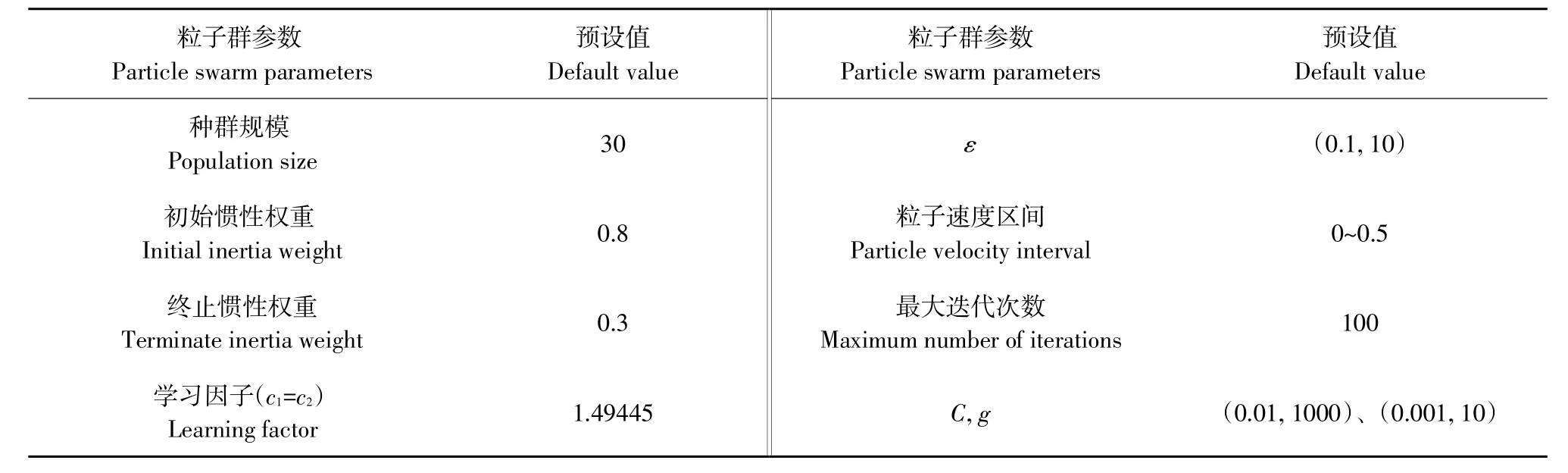
表3 PSO-SVR算法参数预设值Table3 PSO-SVR algorithm parameter preset value
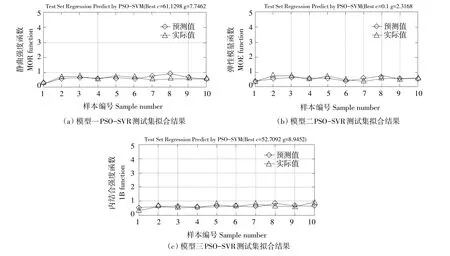
图3 三种PSO-SVR模型测试集拟合结果Fig.3 Test set fitting resultsof three PSO-SVR models
三种PSO-SVR预测模型适应度曲线分别如图4(a)、(b)、(c)所示。可见,经100次进化计算,混合材料板静曲强度、弹性模量、内结合强度PSO-SVR预测模型均可得到稳定适应度迭代值,模型一最优参数C=61.1298、g=7.7462,模型二最优参数C=0.1、g=2.3168,模型三最优参数C=52.7092、g=8.9452。三种PSO-SVR预测模型分别经21、8、12次迭代后适应度函数快速收敛并趋于稳定,即PSO算法优化SVR参数收敛速度快且稳定,适于SVR参数C与g寻优。
3.3 PSO-SVR预测结果分析
通过对训练集30组数据分析,混合材料板静曲强度、弹性模量、内结合强度实际值和预测值误差较小,均方误差分别为0.014、0.009、0.009;拟合优度分别为0.934、0.934、0.949;均方根误差分别为0.12、0.03、0.03。测试集实际值与误差值拟合结果如图3(a)、(b)、(c)所示。测试集10组数据分析可见,预测值与实际值差值较小,均方误差分别为0.018、0.014、0.015;预测值拟合曲线与实际曲线基本吻合,拟合优度分别为0.902、0.918、0.916;模型预测值与实际值误差小,均方根误差分别为0.134、0.118、0.122,模型预测误差小、精度高。相比较SVR,数据集均方误差均减小,预测精度更高;拟合优度更接近1,说明回归函数对数据拟合效果更好。结果表明,以热压压力、热压温度、含水率、热压时间作为模型输入参数,经PSO-SVR模拟预测,混合材料板静曲强度、弹性模量、内结合强度预测值与实际值误差较小,模型预测精度高,反映混合材料板力学特性实际情况,适用性较好。
3.4 SVR和PSO-SVR预测效果对比
为验证PSO-SVR预测模型比SVR模型更适于混合材料板力学特性预测,本文分别用SVR和PSO-SVR算法模拟预测试验数据,分别以训练集和测试集均方误差、拟合优度作为预测模型评价指标,SVR与PSO-SVR预测结果见表4。由表4可知,混合材料板静曲强度、弹性模量、内结合强度PSO-SVR预测模型均方误差分别为0.018、0.014、0.015,拟合优度分别为0.902、0.918、0.916;相较SVR算法,均方误差分别降低0.006、0.009、0.003,拟合优度分别提升12、15、8个百分点。由于BP神经网络需大量训练样本数据且存在收敛速度慢及网格搜索法易陷入局部最优等问题。本文利用支持向量机对混合材料板热压试验数据训练学习,选择粒子群算法对支持向量机参数与g全局优化选择,得到混合材料板力学特性PSO-SVR预测模型。相比较SVR模型,PSO-SVR模型稳定性更强、精度更高、泛化能力更强。

图4 三种PSO-SVR模型进化曲线Fig.4 Evolution curvesof three PSO-SVR models

表4 SVR与PSO-SVR预测结果对比Table4 Comparison of SVR and PSO-SVR predictiveresults
4 结 论
a.将粒子群算法(PSO)嵌入支持向量机回归(SVR)模型参数优化过程,结合正交试验设计理论,根据混合材料板热压生产过程主要工艺参数,构建混合材料板力学特性SVR预测模型,三种SVR预测模型测试集均方误差分别为0.018、0.014、0.015,拟合优度分别为0.902,0.917,0.916。
b.运用PSO算法对SVR模型参数与g选择优化,得到全局最优解,提高模型预测精度。与SVR相比较,PSO-SVR算法模型可更好模拟混合材料板热压过程自变量与因变量非线性关系,预测精度更高、稳定性更强、泛化能力更强。说明粒子群算法适合混合材料板力学特性SVR预测模型参数优化。
c.PSO-SVR模型可为混合材料板力学特性预测及热压控制参数选择提供依据。农林废弃物经一定化学和机械处理可制取高性能纤维,利用其生产混合材料板,增加农业生产附加值,提高农业废弃物综合利用率,降低其处理不当对生态环境影响。该研究成果可为农林废弃物混合材料板力学特性预测及热压控制参数选择优化提供理论参考。
[1] 傅万四,王晓军,南生春,等.发展人造板产业,产促进林业建设[J].木材工业2004,18(1):12-15.
[2] 孙红敏,吴静婷,李晓明.基于改进BP神经网络的价格预测模型研究[J].东北农业大学学报,2013,44(8):133-137.
[3] Steve K,Bruce M A.Press monitoring system for panel industry[C].26th International Particleboard/Composite Materials Symposium,1992.
[4]陈天全.大片刨花板热压过程温度、气压和含水率变化规律研究[D].北京:北京林业大学,2006.
[5] 王东林,俞国胜,杨桦.基于WinCC的中密度纤维板热压工段监控软件的设计[J].林产工业,2009,36(6):37-39.
[6] 王宁,孙丽萍.中密度纤维板热机压力模糊控制研究[J].机电产品开发与创新,2010,23(1):129-131.
[7] Harless T,Wagner E,Short P,et al.Heat and moisture movement in wood composite material during the pressing operation[J].Wood and Fiber Science,1987,19:81-92.
[8] Humphrey P,Bolton A.The hot pressing of dry formed based composite.Part li.A simulation model for heat and moisture transfer and typical results[J].Holzforschung,1989,43(3):199-206.
[9]Zombori B,Kamke F,Watson L.Simulation of the internal conditions during the Hot-pressing process[J].Wood and Fiber Science,2003,35(1):20-23.
[10] 谢力生,李翠翠.纤维板热压中心层温度与力学性能的关系[J].中南林业科技大学学报,2009,29(5):82-86.
[11] 刘亚秋,王春晓,武曲,等.基于Burgers模型的MDF连续平压质量控制计算方法研究[J].安徽农业科学,2014,42(16):5088-5091.
[12] 田燕青.中密度纤维板热压控制参数优化系统的研究[D].哈尔滨:东北林业大学,2011.
[13] 盖玲,宋孝周.基于BP神经网络的棉秆重组方材性能预测研究[J].木材加工机械,2014,43(4):115-119.
[14] 孙建飞,肖生苓,王昊宇,等.工艺类参数对稻壳—木刨花复合包装板力学性能的影响[J].东北林业大学学报,2015,43(2):91-97.
[15] 符彬,郑霞,潘亚鸽,等.无胶蔗渣纤维板制备及性能[J].林产工业,2015,42(6):14-17.
[16] Tiryaki S,Aras U,Kalaycıoglu H,et al.Predictive models for modulus of rupture and modulus of elasticity of particleboard manufactured in different pressing conditions[J].High Temperature Materials&Processes,2016,36:1-12.
[17] 潘亚鸽,朱凌波,唐钱,等.麦秸/木材均质复合无机碎料板的制备及其性能[J].材料导报,2017,31(4):25-29.
[18] 彭顺,桂成胜,林新青,等.大豆胶制备竹刨花板的工艺参数探究[J].林产工业,2017,44(9):19-23.
[19] 孙建平,王逢瑚,胡英成,等.基于遗传神经网络的农作物秸秆板材优化设计[J].农业工程学报,2010,26(1):319-323.
[20] 孙建平,王逢瑚,李鹏,等.遗传神经网络在木塑复合材料力学性能预测中的应用[J].高分子材料科学与工程,2012,28(1):117-120.
[21] 于海英.MDF热压过程多传感器数据融合模型建立与仿真研究[D].哈尔滨:东北林业大学,2013.
[22] Li Q F,Liu Y Q,Zhu L K.Model building and optimization analysis of MDF continuous Hot-pressing by neural network[J].Mathematical Problemsin Engineering,2016:1-16.
[23] Vapnik V N.The nature of statistical learning theory[J].IEEE Transactionson Neural Networks,1997,8(6):153-168.
[24] 赵开才,石凤梅,孟庆林,等.基于SVM的水稻稻瘟病识别方法[J].东北农业大学学报,2013,44(11):118-126.
[25] Smola A J,Schölkopf B.A tutorial on support vector regression[J].Statisticsand Computing,2004,14(3):199-222.
[26] Zhang Y T,Liu CY,Wei SS.ECGquality assessment based on a kernel support vector machine[J].Computers&Electronics,2014,15(7):564-573.
[27] 王德福,王沫,李利桥.锤片式粉碎机粉碎玉米秸秆机理分析与参数优化[J].农业机械学报,2017,48(11):165-171.
[28] 李珂,邰能灵,张沈习.基于改进粒子群算法的配电网综合运行优化[J].上海交通大学学报,2017,51(8):43-45.
[29] 刘环宇,陈海涛,闵诗尧,等.基于PSO-SVR的植物纤维地膜抗张强度预测研究[J].农业机械学报,2017:48(4):30-35.
[30] 谷文成,柴宝仁,滕艳平.基于粒子群优化算法的支持向量机研究[J].北京理工大学学报,2014,34(7):68-73.
[31] 李静,王京,杨磊,等.热处理炉钢板温度的自适应混沌粒子群算法-最小二乘支持向量机优化预报算[J].控制理论与应用,2011:28(12):12-20.

