具有时滞的双向联想记忆神经网络的稳定性分析

杨金祥

(西南民族大学计算机科学与技术学院，四川 成都 610041)

1982年，Hopfield提出了可用作联想存储器的Hopfield神经网络模型，该网络模型可以模拟人类的记忆.1987年，在Hopfield神经网络单层单向联想记忆的基础上，Kosko提出了双层双向联想记忆的神经网络模型(BAM).BAM神经网络在模式分类和模式识别、人工智能等方面有很更广泛的应用，有力地推动了神经网络理论的发展[1-4].神经网络的稳定性与权值有关，通过调整权值，可以使神经网络收敛于平衡点.BAM神经网络的稳定性已引起了广泛的注意，并得到了一系列的研究成果[5-13].本文考虑如下的具有时滞的BAM神经网络:

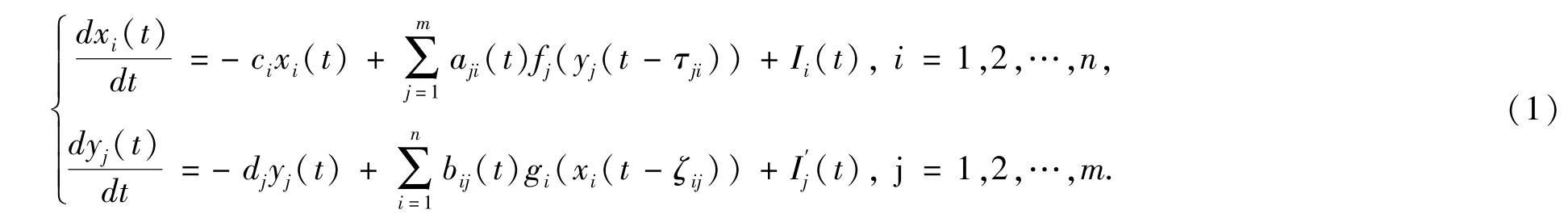
其中xi(t)，yj(t)为状态变量，ci>0，dj>0为常数，τji，ζij是时滞，aji(t)，bij(t) 是连接权，Ii(t) ，(t)是外部输入，fj和gi是激活函数，且满足:系统(1)的初始条件:

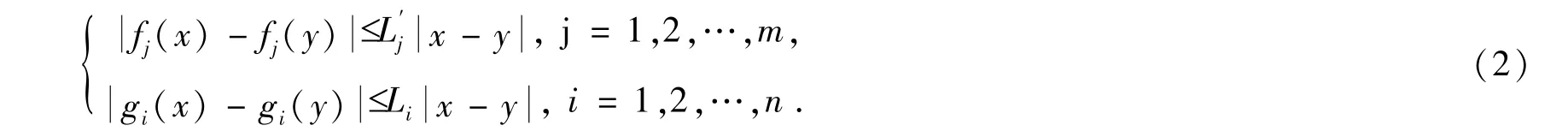
1 准备

2 主要结论

因此，系统(1)是全局指数稳定的.

定理2系统(1)不存在平衡点，且存在常数δi>0，δ′j>0，h>0，使得

矛盾，这就证明(9)成立.于是当k＝0时(8)成立.

第二步假设k(0≤k

3 结语

本文研究一类具有时滞变系数双向联想记忆神经网络的稳定性问题.通过构造Lyapunov函数，在系统存在平衡点时给出了系统指数稳定的充分条件，在系统不存在平衡点时给出了系统的吸引域.

[1]KOSKO B.Adptive bi-directional associative memories[J].Applied Optics，1987，26(23):4947-4960.

[2]KOSKO B.Bi-directional associative memory[J].IEEE Transactions on Systems Man ＆ Cybernetics，1988，18(1):49-60.

[3]KOSKO B.Neural networks and fuzzy systems:a dynamical systems approach to machine intelligence[M].Prentice Hall，1992.

[4]刘汉军，吴海锋，王阳.基于3种训练神经网络方法解决异或问题的研究[J].云南民族大学学报(自然科学版)，2016，25(03):270-274.

[5]CAO J，DONG M.Exponential stability of delayed bi-directional associative memory networks[J].Applied Mathematics ＆ Computation，2003，135(1):105-112.

[6]周立群，具比例时滞杂交双向联想记忆神经网络的全局指数稳定性[J].电子学报，2014，42(1):96-101.

[7]马德印，梁艳春，管仁初，赵笑奢，时小虎，基于模糊理论和双向联想记忆神经网络的变压器老化评价[J]，吉林大学学报，2013，43(5):1331-1337.

[8]李建军，杨志春，双向联想记忆神经网络的指数输入-状态稳定性[J].重庆师范大学学报，2016，33(4):79-84.

[9]贾秀玲.一类带有时滞的模糊双向联想记忆神经网络模型周期解的全局指数稳定性[J].新乡学院学报，2017，34(6):10-12.

[10]谭亮，钟守铭.一类具有离散时滞和分布时滞的BAM神经网络的全局耗散分析[J].四川师范大学学报(自然科学版)，2017，40(1):11-17.

[11]牟天伟，饶若峰.不动点原理在时滞BAM神经网络稳定性分析中的一个应用[J].西南大学学报(自然科学版)，2017，39(6):5-9.

[12]李倩，李东，王娴.分数阶BAM神经网络的全局渐进稳定性[J].重庆工商大学学报(自然科学版)，2017，34(1):21-26.

[13]黄卫华.基于等价关系的双粒度粗糙集模型[J].云南民族大学学报(自然科学版)，2017，26(01):41-45.