交直流混合电力系统的高维多目标最优潮流

周 莹， 邵广惠， 徐兴伟， 侯凯元， 张弘鲲， 张 凡

(1.国家电网东北电力调控分中心, 辽宁 沈阳 110000；2.国网黑龙江电力公司， 黑龙江 哈尔滨 150000；3.新能源电力系统国家重点实验室(华北电力大学)，河北 保定 071003)

0 引言

目前南方电网西电东送已经形成“八条交流、九条直流”17条500 kV及以上大通道，送电规模超过39.5 GW。通过交流输电与直流输电配合进行混合输电已成为区域电网互联的主要方式。而高压直流输电对于远距离大规模传输电能具有巨大优势。随着全球能源互联网的提出和发展，未来必将建设更多的高压直流输电工程以连接区域乃至国家之间的电网，交直流混合电力系统的优化问题受到广泛关注。

传统单目标优化不能很好地考虑多个目标的权衡，所求出的某个目标的最优解往往会导致其他一些目标无法令人满意。故综合考虑多个目标并求取其Pareto最优解以供决策者参考是广泛流行的优化思路[1-3]。目前交流系统多目标优化的研究已经十分成熟[4-10]，但交直流系统多目标优化的研究尚处在起步阶段，相关研究较少。例如，文献[11]将交直流多目标优化问题通过加权等方法转换为单目标优化问题求解，这种先验法不可避免地存在一些弊端。文献[12,13]则分别通过INNC法和NBI法将多目标问题转化为单目标问题再进行求解。

另外，文献[14,15]建立了求解VSC-HVDC系统的两目标优化模型，且均采用NSGA-II求解。目前还未见有文章研究含HVDC的交直流系统的高维多目标(many-objective,一般指三目标以上)优化问题，而VSC-HVDC的实际工程应用相对还较少。另外NSGA-II算法[16]自提出以来虽然由于其良好的性能得到了广泛应用，但NSGA-II通过计算拥挤距离来保证Pareto解集的良好分布，而确定解的拥挤距离首先要判断各解的相邻解，在计算高维多目标问题时这一步骤的计算复杂度将急剧提升，为解决这一问题，Deb等人于2014年提出了NSGA-III算法[17,18]，该算法维持了NSGA-II原有的精英保留和适应度分级机制，主要改进了选择机制，因此其收敛能力是有保障的。NSGA-III通过设置参考点并判断各解到参考点之间的相对距离来确定非支配解，而无需判断相邻解并计算拥挤距离，且其已被证明在最坏场景下的计算复杂度不超过NSGA-II，即MN2(M为目标个数，N为种群规模)。目前鲜有将NSGA-III用于工程实际的相关报道。

基于此，本文建立了含HVDC的交直流系统的四目标最优潮流求解模型，将NSGA-III用于求取其Pareto最优解集，并采用逼近理想解的排序方法(technique for order preference by similarity to ideal solution，TOPSIS)[19]确定最终方案供决策者参考。

1 交直流系统的数学模型

1.1 直流系统方程

交直流系统的结构图如图1所示。

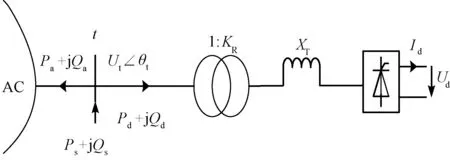
图1 交直流系统结构图

HVDC满足下列方程组:

UdR=kRUtRcosα-XRId

(1)

UdI=kIUtIcosγ-XIId

(2)

UdR=UdI+RdId

(3)

式中:UdR和UdI分别为整流侧和逆变侧的直流电压;UtR和UtI分别为与整流侧和逆变侧相连的交流母线的电压;kR和kI分别为与整流侧换流变压器变比和逆变侧换流变压器变比有关的系数;α和γ分别为整流侧触发角和逆变侧熄弧角;XR和XI分别为整流侧换相电抗和逆变侧换相电抗;Id为直流电流;Rd为直流线路电阻。

可见，交直流混联系统较一般的纯交流系统多了7个变量和3个独立方程。因此必须确定整流侧和逆变侧相应的控制方式才能进行求解。

1.2 目标函数

(1)发电机成本

发电机的发电/燃料成本可表示为：

(4)

式中:ri为发电机i的发电(燃料)成本;NG为发电机数目；PGi为第i台发电机的有功出力；ai、bi和ci为发电机i的成本系数。

(2)电压偏移

(5)

式中:NB为PQ节点的数目;VBi为PQ节点i的节点电压(标幺值)。

(3)电压稳定度

取交直流电力系统雅克比矩阵的最小奇异值作为电压稳定度指标[10]。

f3=max|eig(J)|

(6)

式中:J为收敛潮流的雅克比矩阵。

(4)有功网损

考虑到换流站损耗所占比重较小，取交流线路损耗和直流线路损耗之和作为系统总损耗:

(7)

式中：PacL为交流系统的有功网损。

本文交直流潮流计算方法采用统一迭代法，并采用罚函数方程来处理状态变量的不等式约束问题。罚函数表示如下:

HS=ηPHP+ηQHQ+ηVHV

(8)

(9)

(10)

(11)

对于发电机成本、电压偏移和有功网损3个越小越优型目标，可将惩罚项直接叠加在目标函数上以不断减小惩罚项。即令实际目标Ji为：

Ji=min(fi+HS),i=1,2,4

(12)

而对于电压稳定度这样的越大越优型目标，将惩罚项叠加在目标函数上反而使越限状况越发严重。故令实际目标J3为：

(13)

1.3 约束条件

含HVDC的交直流电力系统的等式及不等式约束条件详见文献[11]，此处不再赘述。

2 算法模型

2.1 NSGA-III算法

在原始的NSGA-II算法中，第t代的父代种群Pt和其通过交叉变异产生的子代种群Qt均含有N个个体。产生下一代Pt+1时，首先将父子两代合并得含有2N个个体的集合Rt=Pt∪Qt。然后将Rt中的个体根据不同的非支配水平进行分级并得到F1,F2,…，Fn，再按照非支配水平由高到低依次选择各级加入St，直到St的规模等于或大于N。假设最后被包括在St中的一级是Fl，则Fl+1及以上的各级均被淘汰。若此时St的规模为N，则下一代Pt+1=St。但实际上在大多数情况下St的规模不会恰好是N，即Fl中只能有K=N-|∪l-1i=1Fi|个解被接受。在非支配水平相同的情况下，应该优先选择那些多样性较好的解以使Pareto前沿尽可能的均匀。在NSGA-II中，这一机制是通过计算Fl中各个解的拥挤距离，并优先选择拥挤距离较大的解来实现的。

NSGA-III维持了上述的精英保留和适应度分级机制，但不计算拥挤距离，而是通过预先设置一组参考点来实现解分布的多样性和均匀性。这组参考点可以通过结构化的方式自动生成，也可以根据决策者的偏好事先指定。当自动生成参考点时，先将各目标归一化，然后在一个归一化超平面(即M-1维的单纯形)上均匀产生参考点。各目标通过下式进行归一化：

(14)

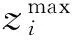
(15)

参考点的具体分布方式见文献[20]。例如，对于一个三目标优化问题，如果每个目标轴被分为4份，则会产生15个参考点，如图2所示。

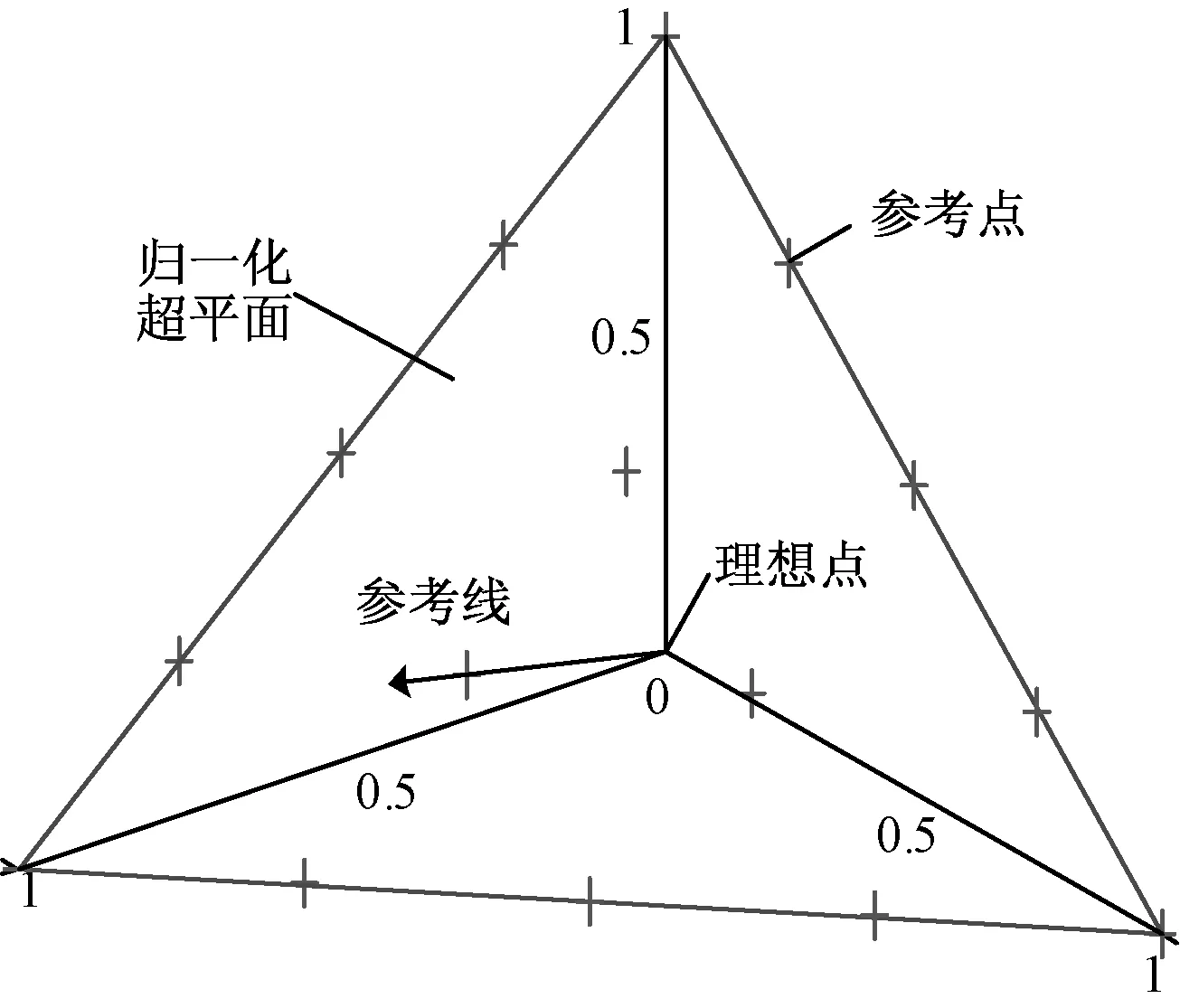
图2 参考点分布图

定义原点到各参考点的连线为参考线，则每个参考点都对应一条参考线。计算St中的每个解到各参考线的垂直距离，使每个解都与距离其最短的参考线所对应的参考点联系起来。这样，在选择Fl中能被接受的解时，优先选择那些有较少的解与其联系的参考点周围的解，而在某参考点附近选择时优先选择距离其最近的点，以保证Pareto解集分布的多样性和均匀性。具体计算过程可参考文献[17]，NSGA-III的伪代码如下:

1: St=Ø, i=1

2: Qt=Recombination&Mutation(Pt)

3: Rt=Pt∪Qt

4: (F1, F2,… Fn)=Non-dominated-sort(Rt)

5: repeat

6: St=St∪ Fiand i=i +1

7: until |St| ≥ N

8: Last front to be included is Fl

9: if |St|=N then

10: Pt+1=St, break

11: else

12: Pt+1=∪ l-1 j=1Fj

13: Points to be chosen from Fl: K=N -|Pt+1|

14: Normalize objectives and create reference set Zr

15: Associate each member s of Stwith a reference point

16: Compute niche count of reference point j∈Zr

17: Choose K members one at a time from Flto construct Pt+1

18: end if

2.2 多目标优化定义

不失一般性，求解多目标优化问题的Pareto解集时依据的4个主要定义如下：

定义1(Pareto支配):设有2个解向量x和y，当且仅当:

∀i∈{1,2,…,k}:fi(x)≤

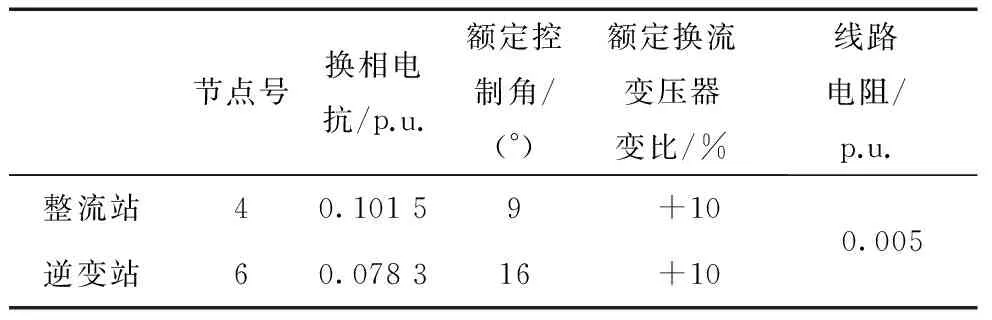
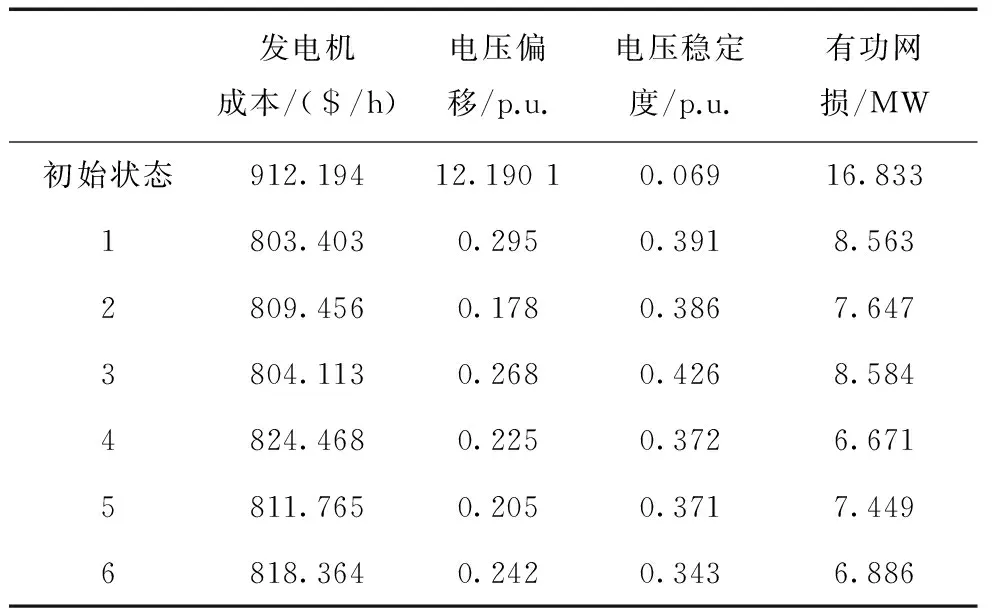
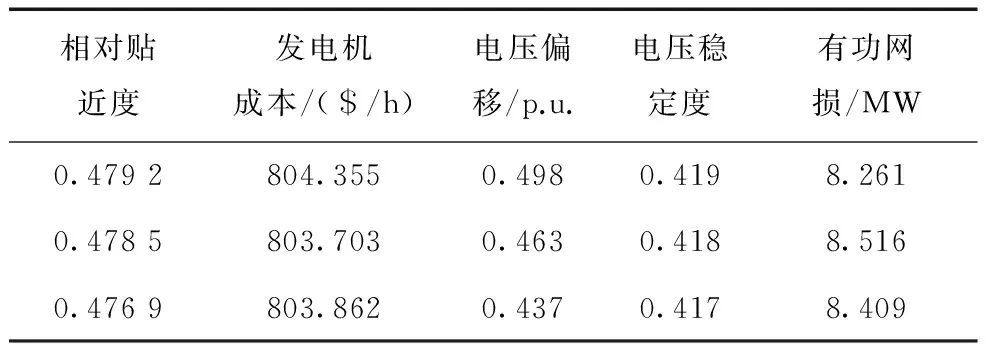
fi(y)∧∃i∈{1,2,…,k}:fi(x)

(16)

时，称解向量x支配解向量y(记作xy)。

定义2(Pareto最优): 对于某解x∈X，当且仅当：

{!∃y∈X|yx}

(17)

时x被称为Pareto最优解。

定义3(Pareto最优解集):解集X中的任意解向量均不能被支配时，则X为Pareto最优解集。

定义4(Pareto前端):设X为Pareto最优解集，则：

Pf={f(x)|x∈X}

(18)

被称为Pareto前端。

2.3 TOPSIS决策法

TOPSIS是一种适合多指标多方案决策分析的系统评价方法。其主要思想是分别取各个指标中最好和最差的解组成虚拟的“正理想解”和“负理想解”，然后计算各个候选方案到“正理想解”和“负理想解”之间的加权欧氏距离，进而得到各方案与正理想解的接近程度，并据此判断各方案的优劣。该法由于思路清晰，计算简便，在各类多目标决策领域得到了广泛的应用。其计算步骤如下:

1)设样本数为m，评价指标数为n，相对应的指标值为xij，首先构建指标矩阵X=(xij)m×n；

2)无量纲化指标矩阵得到V=(vij)m×n。

对于越大越优型指标:

(19)

对于越小越优型指标:

(20)

3)确定指标权重向量W=(w1,w2,…,wn)T，此处的指标权重确定可以使用熵权法等客观赋权法，也可使用序关系法等主观赋权法；

4)计算加权决策矩阵R=(rij)m×n=(wj×vij)m×n；

5)取越大越优型指标的最大值和越小越优型指标的最小值组成正理想解S+j，取越大越优型指标的最小值和越小越优型指标的最大值组成负理想解S-j；

(21)

(22)

进而得到各方案与正理想解的相对贴近度ηi：

(23)

ηi越大说明决策方案Mi越接近正理想解，即方案越优。

3 算例分析

本文所用算例为一加入直流线路的IEEE30节点系统[21]。去掉原系统中节点4和节点6之间的交流线路并替换为直流线路，以节点4为整流站，节点6为逆变站。直流线路参数如表1所示。

表1 直流线路参数

如前所述，交直流混联系统较一般的交流系统多了7个变量和3个独立方程。故需再确定4个已知量才能求解。假设换流变压器变比为额定值不作调节，则还需确定两个已知量，本文采用较常见的整流侧定电流，逆变侧定电压(通常控制整流侧电压为恒定[22])的控制方式。各控制变量及其上下限约束如表2所示[23]。

表2 各控制变量及其上下限约束

注：变压器变比有1±4×0.025共9档，电容器共5组，每组 1 MVar。

NSGA-III算法的参数设置为:种群规模和迭代次数均为100，变异个体百分数和交叉个体百分数均为50%，变异概率为0.02，p=7(即产生120个参考点)。

迭代结束后得到了87个非支配解。表3列出了部分有代表性的Pareto最优解。其中编号1、2、3、4分别为发电机成本、电压偏移、电压稳定度、有功网损4个目标的极端解。

表3 IEEE30节点系统部分Pareto最优解

由表3可见，本文所设定的4个目标之间是相互矛盾的，无法同时达到最优。然而实际电力系统往往需要综合考虑经济性、安全性及电能质量等因素，所以通过合理的方法选择一个或数个较优解供决策者参考就显得十分必要。

通过TOPSIS法进行决策，并认为4个目标同等重要，取其权重均为0.25。表4列出了从Pareto解集中选择的与正理想解贴近度最大的3个较优解。

表4 由TOPSIS得到的相对较优解

4 结论

(1)研究了含HVDC的交直流混合系统的高维多目标最优潮流求解问题，以发电机成本，电压偏移，电压稳定度和有功网损作为目标，实现了电力系统中多个目标之间的均衡，避免了单目标或少目标优化导致其他指标变差的弊端。

(2)引入了更适合处理高维多目标优化问题的NSGA-III算法来求取其Pareto最优解集，未来可考虑再加入污染气体排放量等其他目标，实现电力系统真正的全局综合优化。

(3)本文假设4个目标具有同等重要性，通过TOPSIS法确定最终方案，选择出相对较优的3个解供决策者参考。然而经测试采用不同的赋权方法得到的最终解会有较大差异，因此在实际赋权时应充分考虑决策者的偏好。

最后值得一提的是，高维多目标优化得到的的Pareto前端的可视化较为困难。文献[17]在求解一些Benchmark函数的高维多目标优化问题时采用目标值路径图(value path plot)来实现可视化，然而实际工程优化问题中各目标的量纲和数值差异巨大，使用目标值路径图效果欠佳，研究相应技术实现高维多目标优化问题的可视化是今后需要解决的问题。

[1]胡旺, GARY G Y, 张鑫. 基于Pareto熵的多目标粒子群优化算法[J].软件学报, 2014，25(5):1025-1050.

[2]杨慧娜, 刘钢. 基于二代非支配排序遗传算法的电子变压器多目标优化[J]. 华北电力大学学报(自然科学版), 2013, 40(5):31-35.

[3]盛四清, 刘梦, 李亮亮. 基于改进NSGA-Ⅱ算法的主动配电系统优化运行[J]. 华北电力大学学报(自然科学版), 2015, 42(5):26-32.

[4]李智欢, 段献忠. 多目标进化算法求解无功优化问题的对比分析[J].中国电机工程学报, 2010, 30(10):57-65.

[5]刘佳, 李丹, 高立群,等. 多目标无功优化的向量评价自适应粒子群算法[J]. 中国电机工程学报, 2008, 28(31):22-28.

[6]邱威, 张建华, 刘念. 自适应多目标差分进化算法在计及电压稳定性的无功优化中的应用[J]. 电网技术, 2011, 35(8):81-87.

[7]李鸿鑫, 李银红, 陈金富,等. 自适应选择进化算法的多目标无功优化方法[J]. 中国电机工程学报, 2013, 33(10):71-78.

[8]陈志旺, 陈林, 白锌,等. 求解约束多目标区间优化的交互多属性决策NSGA-II算法[J]. 控制与决策, 2015, 30(5):865-870.

[9]刘靖. 基于智能算法的电力系统多目标最优潮流研究[D].广州：华南理工大学, 2013.

[10]李娟, 杨琳, 刘金龙,等. 基于自适应混沌粒子群优化算法的多目标无功优化[J].电力系统保护与控制, 2011, 39(9):26-31.

[11]殷茂颖. 基于量子粒子群算法的交直流系统多目标无功优化[D]. 济南：山东大学, 2012.

[12]李清, 刘明波, 杨柳青. 求解交直流互联电网多目标无功优化问题的INNC法[J]. 中国电机工程学报, 2014，34(7):1150-1158

[13]杨柳青, 林舜江, 刘明波,等. 考虑风电接入的大型电力系统多目标动态优化调度[J]. 电工技术学报, 2014, 29(10):286-295.

[14]李扬, 李亚辉, 李国庆,等. 考虑经济性和环境因素的含VSC-HVDC交直流系统多目标最优潮流[J]. 电网技术, 2016, 40(9):2661-2667.

[15]高凯, 韩子娇, 张艳军,等. 含VSC-HVDC的交直流系统多目标最优潮流[J]. 电网与清洁能源, 2016，32(3):98-104.

[16]DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.

[17]DEB K, JAIN H. An evolutionary many objective optimization algorithm using reference point based non-dominated sorting approach, part I: solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601.

[18]JAIN H, DEB K. An evolutionary many objective optimization algorithm using reference point based non-dominated sorting approach, part II: handling constraints and extending to an adaptive approach[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4):602-622.

[19]李彦斌, 于心怡, 王致杰. 采用灰色关联度与TOPSIS法的光伏发电项目风险评价研究[J]. 电网技术, 2013, 37(6):1514-1519.

[20]DAS I, DENNIS J E. Normal-boundary intersection: a new method for generating the Pareto surface in nonlinear multi-criteria optimization problems[J]. Siam Journal on Optimization, 2000, 8(3):631-657.

[21]李衍孜. 交直流混联系统网损计算及无功优化研究[D]. 北京：华北电力大学, 2016.

[22]徐政. 交直流电力系统动态行为分析[M]. 北京：机械工业出版社, 2004.

[23]BOUCHEKARA H R E H. Optimal power flow using black-hole-based optimization approach[M]. Amsterdam:Elsevier Science,2014:879-888.