设计开放性数学作业 促进学生差异发展
□林 俊
“学生的学习,除了听老师的讲解以外,还要靠反复不断的练习。获取知识需要练习,掌握本领更需要练习。”反映的是 “掌握知识、形成技能”的传统作业设计理念。现实中出现的 “作业布置得多、学生做得苦、教师批改得累”的现象,往往是以理解知识和强化技能为指向的,折射的是教师作业设计理念的落后和作业设计能力的缺失。如何避免机械、重复、单调、乏味的低效作业?练什么、怎么练则是绕不过去的两个核心问题。 “怎么练,练什么内容更有意义,要靠老师来设计。”显然,作业设计教师不可缺席,旁人无法代替! “教师设计得好,指导得法,学生事半功倍;教师设计得不好,指导不得法,学生事倍功半。”可见,在作业设计中,教师责任重大、责无旁贷。
传统作业内容机械重复,缺乏挑战性;作业形式呆板枯燥,缺乏趣味性;要求统一僵化,缺乏灵活性。这种落后的作业形式降低了学生的热情,固化了学生的思维,压抑了学生的个性,也与数学课程标准“使不同的人在数学上得到不同的发展”理念相悖。因此,新课改背景下的作业设计应以发展学生的数学核心素养为指南,理念可以前卫一点,内容可以开放一点,要求可以灵活一点,设计开放题就是一个很好的切入点。
答案不固定、条件不完备或者策略多样化的习题,称为开放题,它是与封闭题相对的。目前教材中的开放题还不多,教师需进行设计。设计开放题既可以利用陈题改编,又可以通过对现有开放题的加工得到,还可以根据需要自己独立设计。一份优质的数学作业往往能体现教师一定的专业水平和学术水准。
一、设计情境开放的数学作业,促进学生差异发展
学习的最大动力乃是对所学材料的兴趣。小学生受年龄和心理限制,他们喜欢新颖有趣、形式多样和贴近生活的作业。精心选择现实生活中的材料,设计一些包含情境的数学问题,对于激发学生的求知欲,调动学生的学习积极性大有好处。
翻开教材或各种练习册、试卷,计算类似16×79、2790÷90的练习题比比皆是。如此习题,虽然能有效地训练学生 “两位数乘两位数”和 “除数是两位数的除法”的相关技能,但如果经常做这种枯燥的练习,学生就会觉得数学面目可憎,作业索然无味。因此,笔者认为不妨作如下包装、设计:
列竖式计算下面各题,并将计算结果填到等号后,使等式成立,同时将结果填入短文中,使短文信息完整。
722÷38= 121×16= 130÷26=
209×9= 1210÷22= 317×6=
你知道吗?鲁迅是中国伟大的文学家、思想家和革命家。原名周树人,字豫才,浙江绍兴人。___年出身于破落封建家庭。 ___年前往日本学医,后弃医从文。 ____18年____月,首次用笔名 “鲁迅”发表中国现代文学史上第一篇白话小说 《狂人日记》。 ____年10月病逝于上海,终年____岁。
改造后的练习题,有着浓浓的文化味,在巩固数学知识的同时也与语文学科建立了联系。学生要把这6道题的答案:19,1936,5,1881,55,1902填入介绍鲁迅生平的文字中,既要运用过去学习的年月日知识,又要进行合情推理,由此便拓展了学生的知识面,提高了学生的思维能力。这种别出心裁的设计,使学生感到练习有趣而不乏味、有挑战而不简单。
单调、划一的传统作业题型,往往容易引起视觉疲劳,使学生产生消极应付的心理。如果变换一下题型,从形式到内容来个 “大变脸”,就会使人耳目一新,喜闻乐见,最大限度地吸引学生参与。
如:学习 “百分数”后,就可设计题型,让学生在优美诗文中计算百分数问题。
春水春池满,春时春草生,
春人饮春酒,春鸟弄春色。
(1)请朗诵这首诗,看看哪个字出现得最多?
(2)“春”字出现的次数占全诗总字数的百分之几?
(3)课后找一首诗,使某一个字出现的次数至少占10%,然后有感情地朗读。
这个练习没有止于单纯的纸笔计算练习,而是融“百分数”的计算于优美、开放的诗文情境之中,学生既要找诗,又要读诗,还要计算。语、数结合,趣味无穷。海量的资料检索、不同的诗词阅读、具体的数学运算等实践活动形式,大大丰富了学生的学习方式。
再如 “小数加减法”的课后作业,提供了一家快餐店的午餐食谱,同时标明每种食物的蛋白质含量。
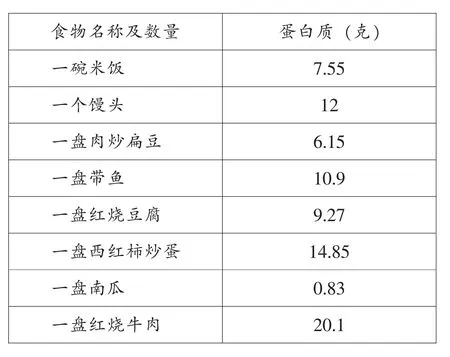
(1)根据自己的口味和饭量选餐,并列竖式计算所订饭菜蛋白质的总含量。
(2)营养学家经过一系列调查研究后发现:7~10岁的儿童一顿饭的蛋白质含量大约需要22.5克。把自己选餐中的蛋白质总量和标准比一比,看是高了,还是低了,并计算相差多少。
(3)看到比较结果,想想你以后选餐需要注意什么。
这样的作业,因为与学生的现实生活紧密相连,所以他们兴致很高;因为与学生的营养状况息息相关,他们都想知道自己喜欢的饭菜蛋白质含量是多少,是否符合规定的标准,所以他们迫不及待地想做。这样的作业自然增强了学生合理膳食的意识,将枯燥的计算与情境相融,很好地调动了学生的学习热情。
二、设计条件开放的数学作业,促进学生差异发展
数学教学的根本目的是教会学生思考,而设计具有低起点、宽入口、有挑战的开放题,能够在传授知识、训练技能的同时,更好地渗透数学思想方法。设计一些具有现实意义、思考价值的开放题——条件开放题、问题开放题、结论开放题及策略开放题,可以面对不同学生的学习现实,促进不同学生的适度提升。条件开放题可以从改编现有封闭题的条件得到,十分方便、快捷。
如:三名选手跳远的成绩:A.3.84米;B.4.01米;C.3.□9米。
(1)谁是第一名,谁是第二名?
(2)如果A是第二名,□里可以填哪些?
(3)如果C是第二名,□里可以填哪些数?
此题由封闭题 “三名选手跳远的成绩:A.3.84米;B.4.01米;C.3.89米。谁是第一名,谁是第二名?”改编而来。把封闭题的一个条件3.89的十分位留白,任学生思维自由驰骋,使每个学生都有得说,有得讲,满足了学生的不同需要。不仅使学生在相互交流中对小数比较大小的方法理解得更加透彻,而且在分析问题、解决问题中渗透了分类思想。
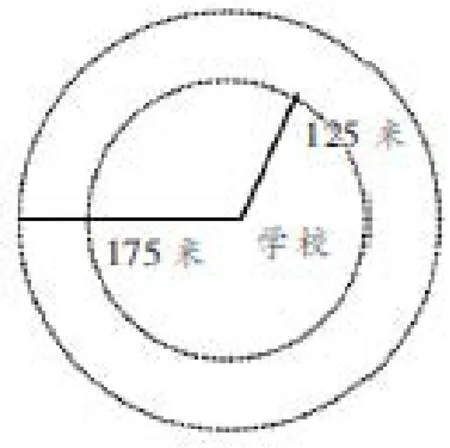
再如:小华家离学校125米,小青家离学校175米,小华家与小青家之间相距多少米?
原题配有插图 (学校在两家之间,且在同一直线上),思维含量不高,学生只需看图列式即可解决问题,涉及的只是低层次思维。当把教材中的插图去掉后得到的条件开放题,思维附加值明显提高。这样,为不同水平的学生提供了展示聪明才智的广阔舞台。
(1)小华家、小青家和学校都在一条直线上,并且都在学校的一侧,则两家相距175-125=50(米);
(2)小华家、小青家和学校都在一条直线上,并且分散在学校的两侧,则两家相距125+175=300(米);
(3)小华家、小青家和学校都不在一条直线上,则两家的距离大于50米,而小于300米。
多数学生受固有思维惯性的影响,可能只是考虑了上述情况 (1)或(2),头脑灵活一点的学生能够考虑这两种情况,水平较高的学生则可能考虑到情况 (3),但不会用圆环图完整地表达所有的情形。通过生生互动,相互补充、不断完善,形成了完整的认知视角;经过教师引领,师生互动,学生思维从片面走向全面,从具体走向抽象,从零散走向统整,令不同层次的学生眼界大开,受到思维风暴的洗礼。
三、设计要求开放的数学作业,促进学生差异发展
由于受多重因素的影响,学生在数学基础、经验和能力等方面都存在差异。为此,设计作业时,不能“一刀切” “齐步走”,而应该从学生的数学现实出发,针对学生的个体差异设计弹性化作业,为每个学生创造一个宽松、自主的练习,提高和发展的人文环境,使每个学生都成为学习的主人,品尝到成功的喜悦,在数学学习历程中不断获得前进的动力。
如新授课上,为了帮助学生记忆和理解公式,培养学生灵活思维的能力,运用公式S=πr2求圆面积时,可设计以下A、B、C三个层次的练习,供不同层次的学生选择。
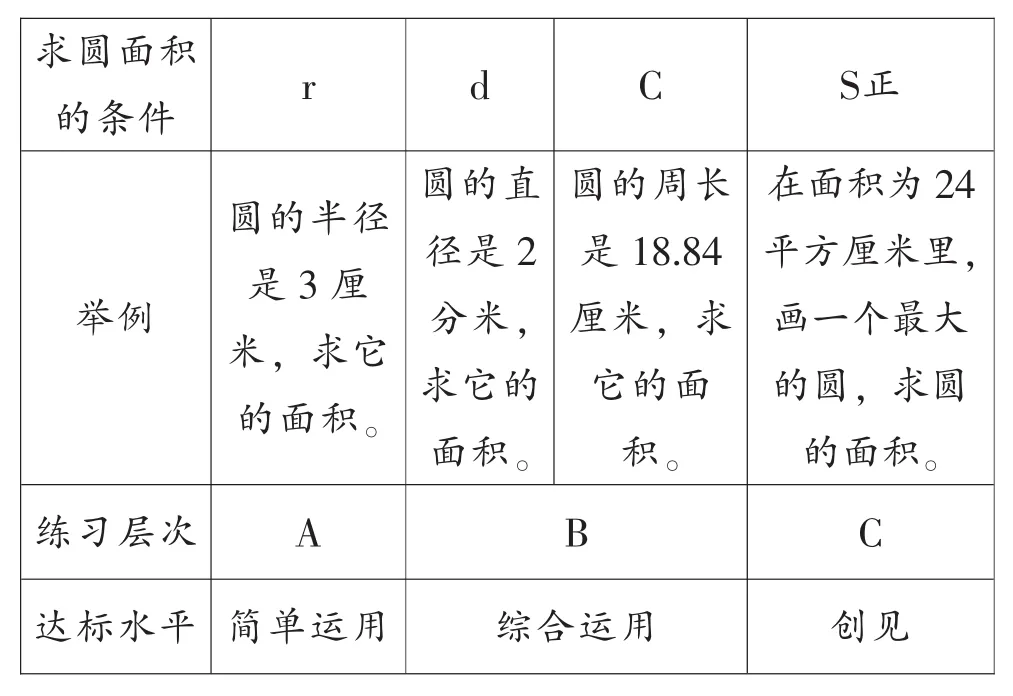
按照美国教育心理学家B.S.布卢姆掌握学习理论,我们把教学目标 (认知目标)水平由低到高分为以下5个层次:识记、领会、简单运用、综合运用和创见。不同层次的学生有不同的选择空间,也有相应的达标要求:学困生至少应该达到A层 (简单运用水平),中等生要达到B层 (综合运用水平),优等生力求达到C层 (创见水平)。
还可以根据不同层次的学生设计模仿练习、变式练习和发展练习三类,学生根据自己的实际情况自由选择适合自己需要的作业。如学习 “长方体和正方体的认识”之后,设计了如下难度渐增的作业:
★一个长方体纸盒的长是5厘米、宽是4厘米、高是3厘米,做这个纸盒需要多少平方厘米的纸?它的体积是多少?
★★一个长方体纸盒的棱长总和是48厘米,长是5厘米、宽是4厘米,它的体积是多少?
★★★一个长方体纸盒的底面积是20平方厘米,底面周长是18厘米,它的表面积是94平方厘米,它的体积是多少?
再如:学习 “亿以内数的认识”后,设计难易不等、弹性极大的开放作业:
用4个 “8”和4个 “0” 摆一摆。
★摆出不同的几个数,写下来,再读一读。
★★按要求摆一个数,写下来,再读一读。
(1)一个 “0”都不读出来的八位数;
(2)只读出一个 “0”的八位数;
(3)读出两个 “0”的八位数;
(4)读出三个 “0”的八位数。
★★★按二星级的要求摆出所有的数,写下来,再读一读。
这种作业可以让不同层次的学生找到适合自己的作业,调动了学生做作业的积极性,树立了学习数学的自信心,享受到作业成功的乐趣。
在 “减负”背景下,还可以在控制作业总量的情况下,通过制订作业选择的规则,鼓励学生完成更具思考性、挑战性的作业,激发自我效能。如 “长方形和正方形的面积”综合练习,8题为一组,其中有6题为一星题、1题为二星题、1题为三星题,由学生自由选择、组合题目来完成6颗星。
★★★从边长10厘米的正方形纸上,剪去一个长3厘米,宽2厘米的长方形,剩下的纸片面积是多少?周长呢?
★★一块长方形和一块正方形的面积相等。已知正方形的边长是6厘米,长方形的宽是4厘米。求长方形的周长。
★一个长方形宽5厘米,长是宽的2倍。求它的周长和面积。
★一个长方形长10分米,宽比长短2分米。求它的面积。
★一个正方形周长是12厘米,它的边长是多少?面积是多少?
★一个长方形面积是48平方分米,宽是6分米,长是多少?
★一个长方形长40厘米,宽3分米,求它的面积。
★一个长方形长6厘米,宽4厘米,它的周长和面积各是多少?
四、设计表征开放的数学作业,促进学生差异发展
表征是学生对问题内隐思考的外在表达,不同学生表征的方式方法是有差异的。表征开放实质上就是解题方式、方法的开放。表征开放的数学作业,为不同学生展露自己的思想、才华提供了大显身手的机会。表征开放的数学作业,教材或配套练习中有的,我们要慧眼识珠,为我所用;如果没有,要加以收集、设计,以更好地照顾学生差异、暴露学生差异、展示学生差异、利用学生差异,在群体交流、互动中,相互欣赏、品味、质疑、碰撞,促进学生差异发展。
一道浅显的题目,也能反映不同学生的思维风格:

图1
图1是用语言表征的。可以看出,答题者是边审题边表征的:看到 “小芳比小云轻一些”,写下 (比)“26kg少”;看到 “小强比小云重一些”,写下 (比)“26kg多”。表达如此及时、简洁。

图2
图2也是用语言表征的,但与图1的区别在于:答题者不是把简洁的表达写在与条件对应的题目之中,而是写在一起的。可以看出写的时候是边写边想的,哪个写在26前,哪个写在26后。这样按照一定的顺序、特定的逻辑排好之后,答案就自然显现出来了。
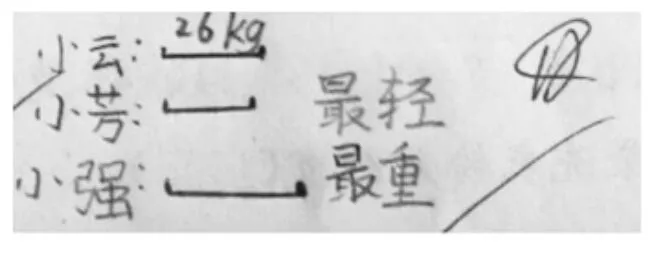
图3
图3是用图形表征的。答题者用一条线段表示小云体重26kg,体重比小云轻的线段就画短一点,比小云重的线段就画长一点。谁最重、最轻看线段的长短一目了然。
再如,学习 “三位数除以一位数” (口算)后,作业中出现了一道思考题。
图4中的大长方形表示420,涂色部分表示多少?
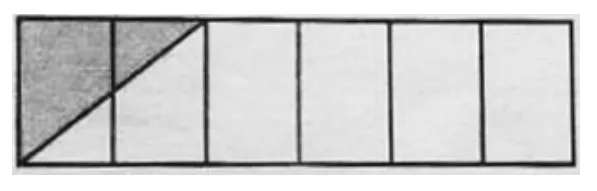
图4
虽然学生答案是一致的,但是想法却多种多样,这可以从他们不同的表征中窥见端倪。
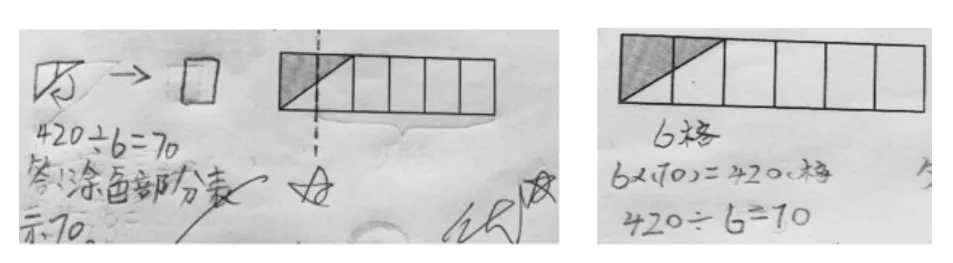
图5
图5一简一繁、一明一暗。左边用图示清楚地表达了阴影部分 (三角形)转化为长方形的过程,而右边则惜墨如金, “6格”二字就高度概括了转化的过程。

图6
图6的2个答题者虽然都把空白的小三角形涂成了黑色,都把阴影部分 (三角形)转化为长方形了,但左边是表示把右边的三角形割下来补到下边,右边表示的是这两个三角形是完全相同的。

图7
显然,图7传递的信息与图6左边表达的意思更加接近,用箭头清楚地表示出割补、旋转的过程。
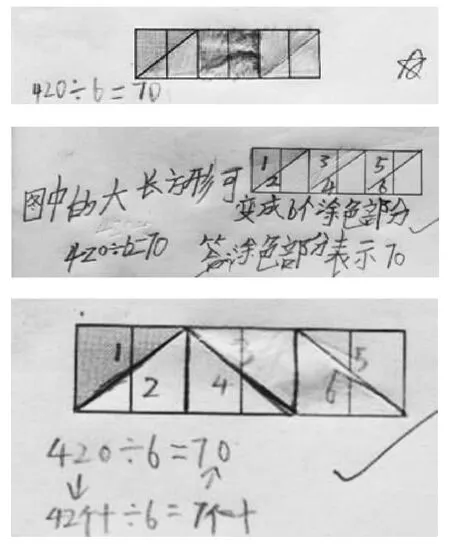
图8
正如学生所言, “图8中的长方形可变成6个涂色部分。”但具体表达有细微差别,有用色彩表示的,有用线段分割的;分割线的方向也有不同。
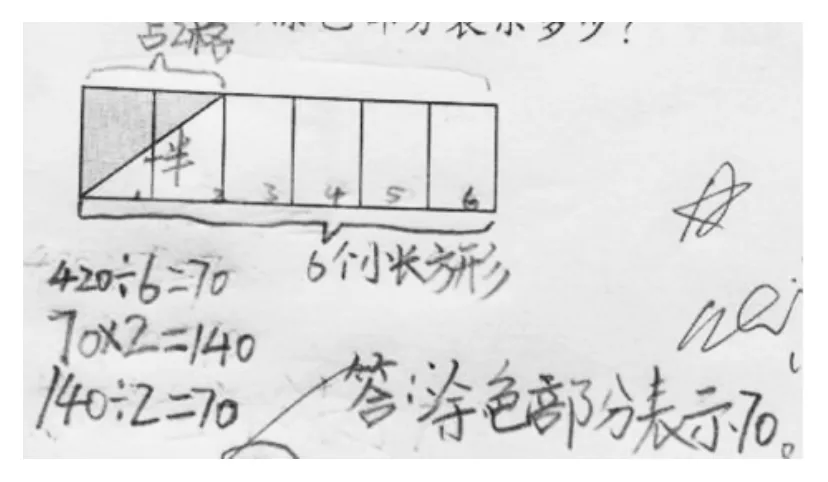
图9
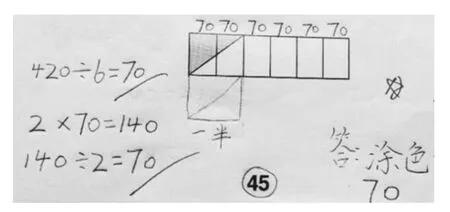
图10
图9、图10中,为什么答题者还用三道算式表示?这两个解答看似多此一举,其实与上面的思路还是不同的。他们是先求出每个小长方形的大小,再求出两个小长方形的大小,最后再求阴影部分的大小(图1中的表征就标示得非常清楚)。因为阴影部分是两个小长方形组成的较大长方形的一半,这可从图10的表征得到印证。
图11中,答题者的思路与上面的截然不同,他们看到的等量关系是阴影部分等于它所在长方形的一半,而不是把阴影部分转化成长方形。

图11
图12中,答题者思路更具独特性:别人看到的是大长方形里有6个小长方形,而他看到的则是3个长方形。他在思考时,能够始终指向问题,压缩思维步骤,这是难能可贵的。虽计算有误,但我还是照样奖励了一个五角星。
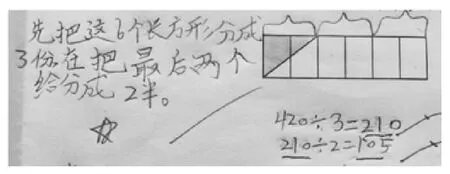
图12
[1]陈朴,潘自由,等.怎样设计小学生的练习和作业[M].南京:江苏教育出版社,1987.
[2]肖川主编.名师作业设计经验[M].北京:教育科学出版社,2007.
[3]方臻,夏雪梅编著.作业设计——基于学生心理机制的学习反馈[M].北京:教育科学出版社,2014.
[4]林俊.数学作业设计的走向:超越传统[N].中国教育报,2013-3-27.
[5]希文.这样的习题好[J].小学数学教师,2005,(6).

