大模数圆柱渐开线齿轮副变位系数的控制
李晓平,贲道春
(江苏鹏飞集团股份有限公司,江苏 海安 226623)
1 引言
传统大模数齿轮设计中的变位系数计算都是以齿轮基本参数为设计依据,不考虑尺寸偏差对变位系数的影响,因而实际的滑动率与理论滑动率存在差异。从这一角度分析可知,即便设计十分完美,实际滑动率大小最终取决于尺寸偏差。对于中心距可适当调整的大模数大型渐开线开式齿轮副,当其中一个齿轮齿形加工超差面临报废将产生重大损失时,如何通过改变另一只齿轮的齿形参数,达到良好的啮合性能,避免超差齿轮报废,很少有人在这一方面进行研究。如何从设计和配对制造两个角度对变位系数进行双重控制,是值得研究的课题。
2 变位系数的设计控制
2.1 总变位系数的分配原则
变位系数是影响滑动率的重要因素[1]。按调整变位系数分配,均衡滑动率来分配变位系数[2],尽可能使滑动率差趋近于0,这是齿轮设计的目标和总变位系数的分配原则。通过多组变位系数分配的滑动率计算数据对比,找到最佳的总变位系数的分配方案,满足滑动率差Δη趋近于0[3]167。
2.2 总变位系数分配和计算机辅助设计

表1 几种齿轮副的变位系数分配Tab.1 Modification Coefficient Distribution of Kinds of Gear Pair(基于Δη≤0.0001,例x∑=1.3,β=6°)
达到滑动率差Δη趋近于0的计算过程繁琐,原始的手工计算方法已经不适应现代设计要求,计算机辅助编程设计是最理想的方法。将获得极小滑动率差的变位系数分配理念编入齿轮计算软件,并能提高计算速度和数据的准确性,将滑动率差的目标值作为迭代精度,并控制迭代精度不大于0.0001,即可求得要求精度的变位系数分配值。基于Δη≤0.0001的几种齿轮的xΣ分配数据(xΣ取1.3时),如表1所示。
2.3 尺寸偏差对Δη的影响及迭代精度分析
滑动率差Δη通常是基于齿形基本尺寸和参数的理论数据,理论滑动率差Δη与实际滑动率差Δη∑(即│η∑1-η∑2│)存在差异,这种差异因齿厚偏差等原因产生。受机床的精度限制,我们很难预知齿轮加工的最终齿形精确尺寸,即很难预知实际滑动率差Δη∑。实际滑动率η∑由理论滑动率和尺寸偏差产生的附加滑动率两部分组成。如何确定理论滑动率差Δη的迭代精度,取决于机床精度和制造控制方法。计算机编程辅助设计具有极高的计算速度,极高的迭代精度虽然不增加设计难度和设计成本,但实际滑动率远大于理论滑动率时,迭代精度再高也没有意义。
加工过程中,公法线长度差值ΔWk与齿轮根圆半径差值Δrf的关系为Δrf=0.5ΔWkctanαn。在大模数齿轮齿形加工中,一般根据该关系确定进刀深度得到最终加工尺寸(如压力角αn为20°的齿轮最终径向进刀深度(Δrf)为1.374ΔWk,压力角αn为25°的齿轮最终径向进刀深度为1.072ΔWk。)。则公法线长度的差值ΔWk与齿轮根圆直径差值Δdf(即2Δrf)的关系为:

式中:Δdf—齿轮根圆直径差值,mm;ΔWk—公法线长度差值,mm;αn—压力角,°。
直齿轮根圆直径差值Δdf与模数mn、变位系数极限差值Δxn的关系为:

式中:Δdf—齿轮根圆直径差值,mm;mn—模数,mm;Δxn—变位系数极限差值。
根据式(1)和式(2)可以推导出变位系数差值Δxn、公法线长度差值ΔWk、模数mn和压力角αn的关系为:

式中:Δxn—变位系数极限差值;ΔWk—公法线长度差值,mm;αn—压力角,°;mn—模数,mm。
总变位系数差值 ΔxΣ为:ΔxΣ=Δx1+Δx2(4)
式中:ΔxΣ—总变位系数差值;Δx1—小齿轮变位系数极限差值;
Δx2—大齿轮变位系数极限差值。
根据式(3)和式(4)及有关滑动率计算公式推导出公法线长度极限偏差尺寸的滑动率η∑n:

式中:ηΣ1—小齿轮公法线长度极限偏差尺寸的滑动率;ηΣ2—大齿轮公法线长度极限偏差尺寸的滑动率;xΣ—原设计总变位系数;ΔxΣ—总变位系数差值;αn—压力角,°。α′—啮合角,°;αa1—小齿轮齿顶圆压力角,°;αa2—大齿轮齿顶圆压力角,°;z1—小齿轮齿数;z2—大齿轮齿数;zΣ—大小齿数和(z1+z2)。
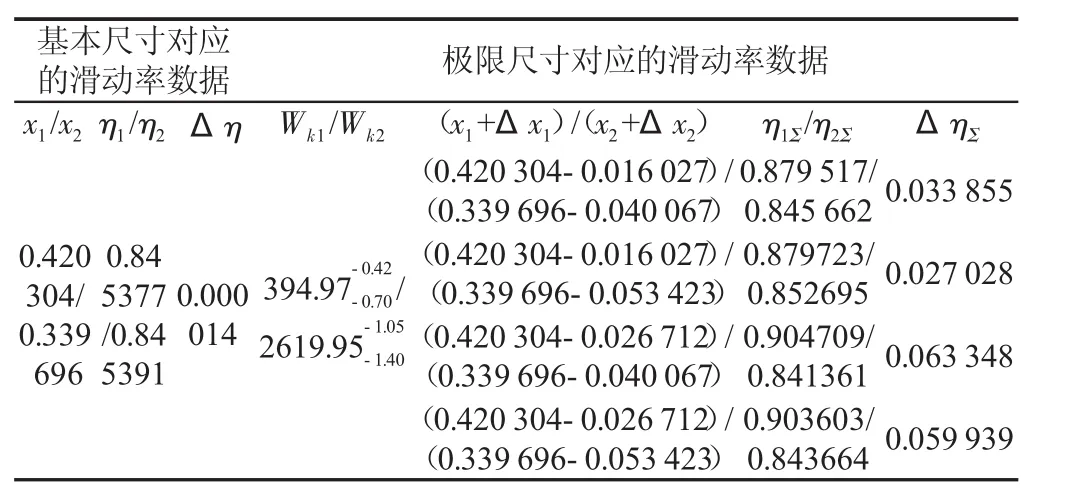
表2 公法线长度极限偏差对滑动率的影响Tab.2 Influence of Base Tangent Length Limit Deviation to Sliding Rate(例:mn=36、z1/z2=23/202、αn=20°、β=0、xΣ=0.76、9-9-8HK/9-9-8KL、计算精度 1/1000000)
根据式(5)和式(6)可以计算出大小齿轮公法线长度上下偏差尺寸对应的4个总滑动率数据。则齿轮副公法线长度上下偏差尺寸对应4种滑动率差Δη∑(即│η∑1-η∑2│)数据。
以回转窑等转筒设备传动齿轮副的直齿轮为例,进行滑动率差 Δη 的迭代精度需求分析:已知:mn=36,z1/z2=23/202、αn=20°、精度等级 9-9-8HK/9-9-8KL[4]6、[5]、6[6]5。公法线长度及其极限偏差为394.97--00..4720和2619.95--11..0450,如表2所示。根据式(3)得到大小齿轮的4种变位系数差Δxn分别为-0.016 027、-0.026 712和-0.040 067、-0.053423。再根据式(4)~式(10)得到公法线极限尺寸对应的 4种滑动率差 Δη∑为 0.033 855、0.027 028 和 0.063 348、0.059 939,范围为(0.027 028~0.063 348)。从表1 中可以看出,公法线长度处于极限值时ΔηΣ最小值约为0.027,计算精度0.01就能满足设计要求。但是该例大小齿轮公法线长度变动公差只有0.08和0.17,远小于公法线长度公差带宽度0.28和0.35,分别约为29%和49%。齿轮副公法线长度变动公差范围内的滑动率差范围是公法线长度极限偏差对应的滑动率差范围的较小区域,因此计算精度0.001就能满足设计要求。如果齿轮副精度等级较高(如8-8-7级或7-7-6等更高等级),或采用高精度机床加工(如磨齿),实际滑动率差Δη∑就远小于0.001;如果采用高精度机床加工,同时又通过改变加工工艺,在加工工程中进行变位系数的搭配控制,滑动率差Δη∑可能小于0.001,迭代精度取0.0001才能满足要求。
3 变位系数的制造控制
3.1 制造尺寸偏差对滑动率差的影响
理论滑动率差Δη为0.000 014,如表1所示。而实际的滑动率差高达(0.027~0.063),相差数百倍,失去了原先高迭代精度设计控制滑动率差Δη的意义。因此,要达到滑动率差趋近于0,需要从制造角度进行控制。
3.2 搭配控制的概念
当齿轮副其中一个齿轮加工完毕,即实际变位系数已经明确的情况下,可以基于滑动率差的控制要求(如Δη≤0.0001),以该齿轮实际测量推算的变位系数为基础数据“量身定制”另一个待加工齿轮,推算一个变位系数搭配值进行配对齿轮的加工。因此搭配控制设计是对一次设计的进一步完善。在回转窑等转筒设备大模数小批量大型齿轮的制造中应用该技术,可以对加工超差齿轮配对制造以避免报废造成巨大损失。大齿轮尺寸控制难度大于小齿轮,且小齿轮的公法线长度变动公差一般小于大齿轮变动公差。因此,为了减小搭配难度,节约加工时间,根据大齿轮的实际变位系数对小齿轮变位系数进行控制较为合理。
3.3 搭配控制计算方法
已加工大齿轮的实际变位系数是控制小齿轮变位系数已知条件。根据大齿轮实际变位系数对小齿轮原先设计的变位系数x1进行微调,找出Δη趋近于0的x1。为了节约计算时间,需比较原先设计的x2和实际值的大小,作为x1微调增减的依据,如表3所示。从表3分析可知,基于Δη=0的齿轮副随着总变位系数xΣ变化分配后x1和x2同时增减。因此变位系数微调规律为同时增减。x1微调达到滑动率差Δη趋近于0的手工计算过程同样繁琐。将η1=η2编入齿轮计算软件,x2作为已知条件,迭代精度取0.0001求得x1,可节省大量计算时间和提高计算数据的准确性。

表3 不同xΣ的齿轮副变位系数变化规律Tab.3 Modification Coefficient Change Rule of Gear Pairs with Different xΣ(例:mn/αn=30/20°、z1/z2=32/216、Δη<0.0001)
3.4 搭配控制的应用前景
搭配控制设计前后滑动率差比较,如表4所示。搭配控制可以消除变位系数的控制“盲区”,能最大限度减小滑动率差。从变位系数搭配控制角度分析,原先的变位系数分配是预设计,可以适当降低迭代计算精度;加工过程中的变位系数搭配设计控制是最终的控制,需要较高的迭代计算精度。特别对于批量小的大型齿轮制造更能显示出搭配控制的优点。用搭配控制法加工齿轮可以增加配对验收项目。

表4 搭配控制设计前后滑动率差比较Tab.4 Comparison of Sliding Rate Difference Before and After Matching Control Design(例:mn=36、z1/z2=23/202、αn=20°、β=0、9-9-8HK/9-9-8KL、计算精度 1/1 000 000、xΣ=0.76)
3.5 搭配控制达到的效果
表4是基于基本尺寸设计和滚切加工搭配控制的滑动率的举例比较。从数据分析可以看出,基于基本尺寸设计的变位系数分配值不考虑尺寸偏差的影响,相当于变位系数存在负值偏差(即0.420 3;搭配控制设计是以公法线长度变动公差对应的变位系数变化量作为正负对称公差(即0.415 634±0.005 342和0.293 466±0.006 6779)为依据的计算值。因此搭配控制的变位系数更接近目标数值。曾经有人利用优化设计思想实现了变位系数的计算机取值[[7];有人提出过齿轮副综合误差的类似概念,介绍用齿轮配对磨削法和齿形选配法[8]来降低齿轮副齿形综合误差;还有人提出过高精度齿轮的精密配对磨齿[9]。但没有人提出过齿轮参数加工搭配法。搭配控制设计方法能尽量排除不定因素影响。搭配控制设计能将基于基本尺寸设计的滑动率差值可能的范围(0.027~0.063)控制到(0~0.018)较小值范围,滑动率差的控制范围缩小70%以上。如果采用高精度机床加工(如磨齿加工),效果更加明显,真正达到精确控制的目的。
4 结论
(1)通过计算机编程计算,可求得总变位系数xΣ分配的优化值,理论滑动率趋近于0,使理论滑动磨损降低。(2)加工过程中采用变位系数搭配控制方法可弥补尺寸偏差对滑动率有较大影响的不足;或者可以对加工超差齿轮的配对制造避免报废。通过计算机编程计算,可求得基于η1=η2的x2的理想搭配值x1。变位系数搭配控制保证实际滑动率差Δη趋近于0的效果比较明显。(3)采用变位系数搭配控制方法制造齿轮副,可增加参数配对检验项目。
[1]宋永乐,李光福,陈晓金.兆瓦级风电齿轮箱齿轮微点蚀分析[J].重庆大学学报,2015(1):120-125.(Song Yong-le,Li Guang-fu,Chen Xiao-jin.Analysis of gear micropitting for megawatt-class wind turbine gearbox[J].Journal of Chongqing University,2015(1):120-125.)
[2]丁江.多面体螺旋曲线啮合齿轮变速器几何学设计理论研究[D].广州:华南理工大学,2014.(Ding Jiang.Study on geometrical design theory of polyhedral helix curve meshing wheel reducer[D].Guangzhou:South China University of Technology,2014.)
[3]贲道春,王冬生,王复光.管磨机齿轮变位系数与螺旋角的设计研究与探讨[J].机械传动,2016,40(1):165-168.(Ben Dao-chun,Wang Dong-sheng,Wang Fu-guang.Discussion and study of design on modification coefficient and helix Angle of gear for tube mill[J].Journal of Mechanical Transmission,2016,40(1):165-168.)
[4]国家建筑材料工业机械标准化技术委员会.JC/T 333—2006水泥工业用回转窑[M].北京:中国建材工业出版社,2006:1-11.(National technical committee on building materials industry mechanics of standardization administration of china.JC/T 333—2006 Rotary Kiln for Cement Industry[M].Beijing:China Building Materials Press,2006:1-11.)
[5]全国建材装备标准化技术委员会.GB/T 27976-2011水泥工业管磨机装备[M].北京:中国标准出版社,2012:1-13.(National technical committee on building materials equipment of standardization administration of china.GB/T 27976-2011 Tube Mill Equipment for Cement Industry[M].Beijing:China Standard Press,2012:1-13.)
[6]国家建筑材料工业机械标准化技术委员会.JC/T 335-2006水泥工业用回转烘干机[M].北京:中国建材工业出版社,2006:1-7.(National technical committee on building materials industry mechanics of standardization administration of china.JC/T 335-2006 Rotary Dryer for Cement Industry[M].Beijing:China Building Materials Press,2006:1-7.)
[7]高顺德,李林林,宋晓光.起重机用行星齿轮变位系数选取方法研究[J].机械设计与制造,2013(1):130-133.(Gao Shun-de,Li Lin-lin,Song Xiao-guang,etc.Research on selection of modification coefficient of planetary reducer gears[J].Machinery Design&Manufacture,2013(1):130-133.)
[8]刘欢.人字齿行星齿轮传动系统误差与齿廓修形研究[D].南京:南京航空航天大学,2014.(Liu Huan.Research on errors and profile modification of herringbone planetary gear train[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2014.)
[9]陶燕光,黎上威,马宪本.高速齿轮热变形修形的试验研究[J].齿轮,1988(2):25-28.(Tao Yan-guang,Li Shang-wei,Ma Xian-ben.Experimental study of correction of high speed gear heat deformation[J].Gear,1988(2):25-28.)

