单调集值测度空间中的Egoroff型定理及Riesz型定理

吴 怡，吴健荣

（苏州科技大学 数理学院，江苏 苏州 215009）

所谓单调测度是指在空集处取值为零的单调集函数，模糊测度[1-3]、非可加测度[4-6]都属于单调测度的范畴。由于实际应用的需要，单调测度理论不断发展，特别是经典测度论中的一些重要收敛定理被先后推广到单调测度空间中。1985年，王震源[1]在上自连续及下自连续的条件下，给出了四种关于模糊测度空间中的Riesz型定理；之后，在文献[2-3]中被进一步推广。2003年，Li[7]给出了一个关于单调集函数的Egoroff定理成立的充分必要条件。而在2004年，Murofushi等人[4]利用强序连续、S性质等概念，讨论了非可加测度空间中的Egoroff定理成立的一些充分（必要）条件。2005年，Song及Li[5]研究了非可加测度空间中四种Lebesgue型定理成立的充要条件。之后，李军及Mesiar[8]在度量空间中给出了关于单调测度的Egoroff定理成立的一个等价条件，并在此基础上得到了关于单调测度的Lusin定理，讨论了单调测度空间中可测函数与连续函数的内在联系。2014年，Takahashi等人[6]在非可加测度空间中得到了Egoroff定理成立的一个新的等价条件。

近年来，Gavrilut等人[9-18]利用集合包含关系将单调测度推广到了集值的情况，并且得到了关于单调集值测度的模糊性、正则性、原子与伪原子、Egoroff型定理及Lusin型定理等方面的丰富成果。而在2004年，郭彩梅和张德利[19]在实数集R的所有非空子集构成的集族P0（R）上定义了一种新的序关系。2008年，高娜，李艳红，王贵君[20]将文献[19]中的序关系推广到了m维正欧式空间P0（R+m）中，讨论了取值于m维正欧式空间的模糊测度的自连续、一致自连续、逆自连续和一致逆自连续。2015年，开学文和吴健荣等人[21]利用以上的序结构，在单调集值测度空间中得到了Lebesgue型定理以及Egoroff型定理，在单调集值测度空间中研究了可测函数几种收敛性之间的关系。之后，吴健荣等人[22]又提出了单调集值测度的原子以及伪原子的概念，给出关于单调集值测度的（N）积分，并探讨了该积分的一些性质。该文是文献[21]的继续。首先，给出关于单调集值测度的Egoroff条件、S*性质、PS*性质、条件M*等概念，并研究了它们之间的关系；在此基础上，给出了单调集值测度空间中Egoroff定理成立的两个新的充分必要条件。其次，针对目前单调集值测度的Riesz定理的成果尚不多见的情况，该文利用S*性质及PS*性质将Riesz定理推广到了单调集值测度空间中。

1 预备知识

该文中，X 表示任一非空集合，Ω 为 X 上的一个 σ-代数，即（X，Ω）为可测空间。 R+m＝{x；x＝（x1，x2，…，xm），xi≥0，i=1,2，3，…，m}表示 m 维正欧式空间，P0（R+m）表示 m 维正欧式空间 R+m中全体非空子集构成的集类。关于m维正欧式空间及其子集类上的运算、序结构及收敛定义如下：，其中其中其中

定义 1[20]设如果满足条件：

定义2[20]设∀A，An∈P0（R+m），若则称A和B拟等价，记为

注 1显然，P0（R+m）中两个拟等价的元素并不一定相等，但等同于

注2“拟等价”是P0（R+m）中的一种等价关系，可作商空间P0（R+m）/≈，将每个等价类中元素不作区分，用一个元素来代表。在此意义下也常写成

定义 3[20]设，若∀ε＞0，∃N∈N，当 n＞N 时，有 A≾An+ε 且 An≾A+ε，则称{An}依序≾收敛于，记为

注3用不等式组且代替文献[20]中的，这是考虑A-ε到未必再属于 P0（R+m）。

注4由注1及注2可知，除极限值为外，上述极限在集合相等意义下一般是不唯一的；若把P0（R+m）中“拟等价”的元素视为同一元素，则极限是唯一的。

定义 4[21]设（X，Ω）为可测空间，集函数 π：满足以下条件：

则称π为（X，Ω）上的单调集值测度，称（X，Ω，π）为单调集值测度空间。

若无特别说明，该文总设（X，Ω，π）为单调集值测度空间，fn（n≥1），f均为定义在（X，Ω，π）上的实值可测函数。

定义 5[21]如果有则称 π 是集值强序连续的。

定义6[21]设π为（X，Ω）上的单调集值测度，

（2）如果存在子集 E⊆X，满足 π（E）={0˜}（分别地，π（XE）=π（X））且在 XE 上， fn收敛于 f，则称{fn}在 X上几乎处处收敛（分别地，伪几乎处处收敛）于 f，记作

（3）如果对∀ε＞0，存在子集 Xε⊆X，满足 π（Xε）≾{ε¯}且在 XXε上，fn一致收敛于 f，则称{fn}在 X 上基本一致收敛于 f，记作

2 关于单调集值测度的Egoroff型定理

首先，在单调集值空间中引入几个新的概念。

定义7设π为（X，Ω）上的单调集值测度，

（1）若∀{An}⊆Ω 满足都存在子列{Ank}⊆{An}，使得则称 π 满足 S*性质。 （2）若∀{An}⊆Ω 满足都存在子列{Ank}⊆{An}，使得则称 π 满足PS*性质。

定义8设π为（X，Ω）上的单调集值测度，如果对于每个双序列满足以下条件：

则∀ε＞0，都存在数列{nm}⊆N+，使得那么称 π 满足 Egoroff条件。

下面将给出一个 Egoroff条件成立的充分条件。 An↓A 且

定理1若单调集值测度π是集值强序连续的且满足S*性质，则π满足Egoroff条件。

证明令双序列满足当 m≥m′，n≤n′时有由于{Anm}关于n递减且 π 是集值强序连续的，所以从而存在正整数 n（m）使得 π（An（m）m）由于 π 满足 S*性质，故存在数列{mk}⊆N+使得由π的强序连续性可知存在j∈N+使得定义数列{nm}⊆N+如下

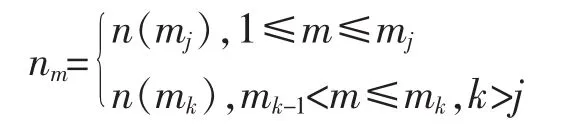
从而

故π满足Egoroff条件。

以下定理给出了Egoroff条件成立的必要条件。

定理2若π满足Egoroff条件，则π是集值强序连续的。

证明假设π满足Egoroff条件，令递减序列{Bn}收敛至集合B且π（B）={0˜}。定义双序列{Anm}如下

由于 π 满足 Egoroff条件，所以∀ε＞0，存在数列{nm}⊆N+，使得

定理3π满足Egoroff条件当且仅当若fn几乎处处收敛于f，则fn基本一致收敛于f。

证明假设Egoroff条件成立并且可测函数列{fn}几乎处处收敛于f。取m，n∈N+，使得

反之，假设若fn几乎处处收敛于f，则fn基本一致收敛于f。令双序列满足当 m≥m′，n≤n′时有且∀ε＞0，定义可测函数

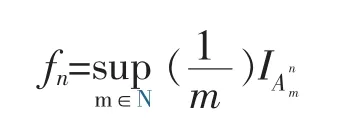
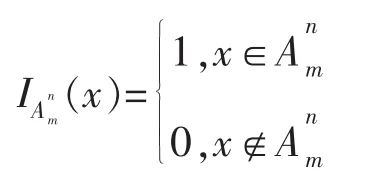
那么，对∀m，n∈N+

下面，定义另一个新的条件且该定义只涉及单序列。

定义9设π为（X，Ω）上的单调集值测度，如果则∀ε＞0，存在严格递增数列{mn}⊆使得则称 π 满足条件 M*。

引理1[6]设（X，Ω）为可测空间。对于任一双序列满足当 m≥m′，n≤n′时有都存在序列{En}使得并且对于任一严格递增的数列{kn}⊆N+，都存在一个数列{ni}⊆N+使得

定理4设π为（X，Ω）上的单调集值测度，那么π满足条件M*当且仅当π满足Egoroff条件。

证明必要性：令双序列满足以下条件：（1）当 m≥m′，n≤n′时有由引理 1 可知存在序列{En}使得对∀n∈N+，En都是可测的且有

由于π满足条件M*，所以∀ε＞0，存在严格递增数列{ln}⊆N+使得由引理 1，存在数列{ni}⊆N+使得从而

下证存在数列{ki}⊆N+使得∀l∈N+，由上述已证，存在数列{kil}⊆N+，使得对∀m∈N+，定义则对任意l＞0的整数和h≥0，总有从而由于且所以由此可知从而有

现在令Ei=Akii，则因为 π 满足条件 M*，所以存在数列{hj}⊆N+使得

故π满足Egoroff条件。

充分性：设序列{En}满足定义双序列{Anm}使得

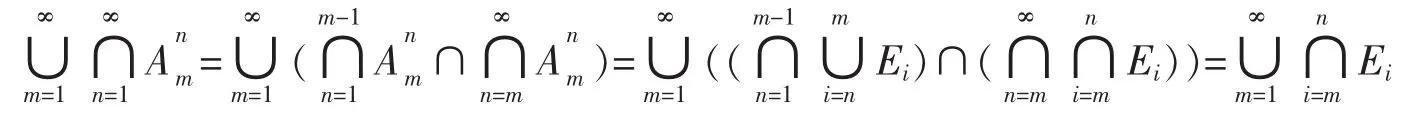
注5由定理3及定理4可知条件M*也是Egoroff定理成立的充要条件。在文献[21]中，开学文等人证明了条件E*为Egoroff定理成立的充要条件，所以Egoroff条件等价于条件M*也等价于条件E*。但是条件M*只涉及到了单序列，而Egoroff条件以及条件E*都是关于双序列的条件，所以文中所提出的条件M*形式更简洁，是对Egoroff定理研究的进一步推广。

3 关于单调集值测度的Riesz型定理

定理5π满足S*性质当且仅当若则存在子序列{fnk}满足

证明充分性：令{An}⊆Ω且

易知fnkm在上收敛于f，即故定理得证。

定理6π满足PS*性质当且仅当若则存在子列{fnk}满足

证明充分性：令{An}⊆Ω且定义

必要性：设 fn→p.πf，则存在递增数列{nk}⊆N+，使得

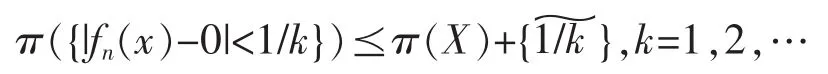
由于 π 满足 PS*性质，所以存在子列{Akm}，使得

[1]WANG Z Y.Asymptotic structural characteristics of fuzzy measures and their applications[J].Fuzzy Sets and Systems，1985，16（3）：277-290.

[2]SUN Q H.Property （S） of fuzzy measure and Riesz’s theorem[J].Fuzzy Sets and Systems，1994，62（1）：117-119.

[3]HA M H，CHENG L X，WANG X Z.Notes on Riesz’s theorem on fuzzy measure space[J].Fuzzy Sets and Systems，1997，90（3）：361-363.

[4]MUROFUSHI T，UCHINO K，ASAHINA S.Conditions for Egoroff’s theorem in non-additive measure theory[J].Fuzzy Sets and Systems，2004，146（1）：135-146.

[5]SONG J J，LI J.Lebesgue theorems in non-additive measure theory[J].Fuzzy Sets and Systems，2005，149（3）：543-548.

[6]TAKAHASHI M，MUROFUSHI T，ASAHINA S.A new necessary and sufficient condition for the Egoroff theorem in non-additive measure theory[J].Fuzzy Sets and Systems，2014，244：34-40.

[7]LI J.A further investigation for Egoroff’s theorem with respect to monotone set functions[J].Kybernetika，2003，39（6）：753-760.

[8]LI J，MESIAR R.Lusin’s theorem on monotone measure spaces[J].Fuzzy Sets and Systems，2011，175（1）：75-86.

[9]GAVRILUT A C.Properties of regularity for multisubmeasures[J].Annals of the Alexandru Ioan Cuza University-Mathematics，2004，50（2）：373-392.

[10]GAVRILUT A C.Non-atomicity and the Darboux property for fuzzy and non-fuzzy Borel/Baire multivalued set functions[J].Fuzzy Sets and Systems，2009，160（9）：1308-1317.

[11]GAVRILUT A C，Croitoru A.Non-atomicity for fuzzy and non-fuzzy multivalued set functions[J].Fuzzy Sets and Systems，2009，160（14）：2106-2116.

[12]GAVRILUT A C.Regularity and autocontinuity of set multifunctions[J].Fuzzy Sets and Systems，2010，161（5）：681-693.

[13]GAVRILUT A C，CROITORU A.Pseudo-atoms and Darboux property for set multifunctions[J].Fuzzy Sets and Systems，2010，161（22）：2897-2908.

[14]GAVRILUT A C.A Lusin type theorem for regular monotone uniformly autocontinuous set multifunctions[J].Fuzzy Sets and Systems，2010，161（22）：2909-2918.

[15]GAVRILUT A C.Abstract regular null-null-additive set multifunctions in Hausdorff topology[J].Annals of the Alexandru Ioan Cuza University－Mathematics，2013，59（1）：129-147.

[16]GAVRILUT A C.Alexandroff theorem in Hausdorff topology for null-null-additive set multifunctions[J].Annals of the Alexandru Ioan Cuza University-Mathematics，2013，59（2）：237-251.

[17]PRECUPANU A，GAVRILUT A C.A set-valued Egoroff type theorem[J].Fuzzy Sets and Systems，2011，175（1）：87-95.

[18]RECUPANU A，GAVRILUT A C.Set-valued Lusin type theorem for null-null-additive set multifunctions[J].Fuzzy Sets and Systems，2012，204：106-116.

[19]GUO C M，ZHANG D L.On set-valued fuzzy measures[J].Information Sciences，2004，160（1-4）：13-25.

[20]高娜，李艳红，王贵君.集值模糊测度的自连续性[J].四川师范大学学报（自然科学版），2008，31（4）：386-389.

[21]开学文，吴健荣，李娇娇.单调集值测度空间上的Lebesgue和Egoroff型定理[J].西南师范大学学报（自然科学版），2015，40（8）：10-16.

[22]WU J R，KAI X W，LI J J.Atoms of monotone set-valued measures and integrals[J].Fuzzy Sets and Systems，2016，304：131-139.